Решение тригонометрических уравнений

1. Решение тригонометрических уравнений

2. Содержание

Уравнения cosx=a
Уравнения sinx=a
содержание

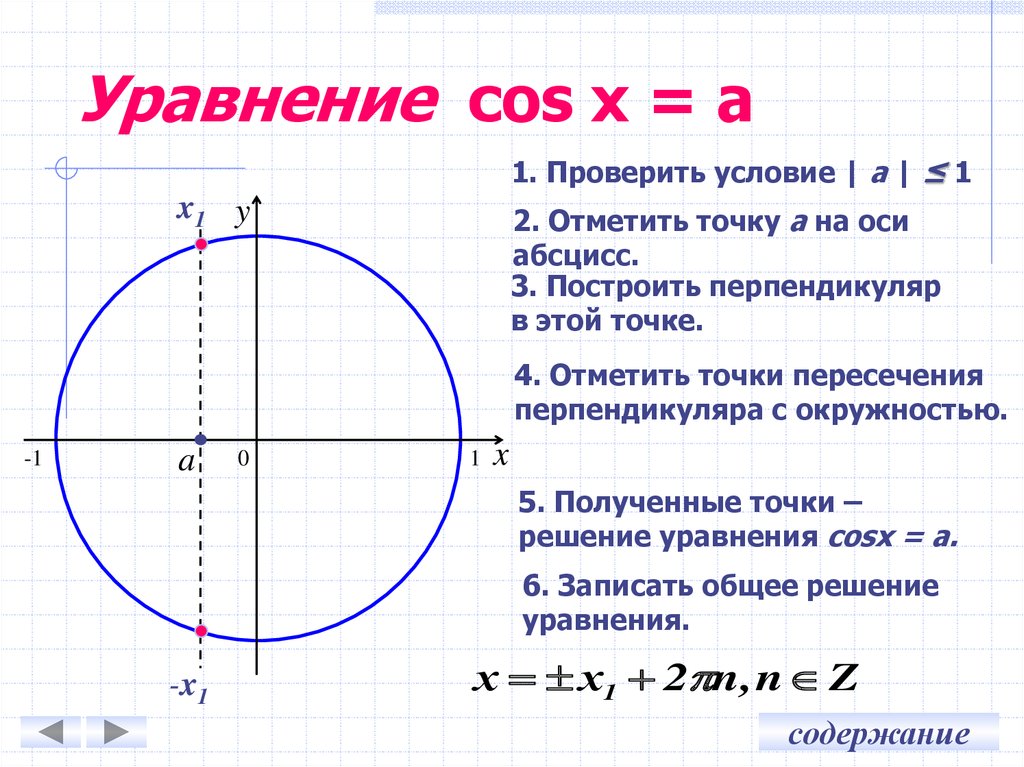
3. Уравнение cos x = a

1. Проверить условие | a | ≤ 1
x1 y
2. Отметить точку а на оси
абсцисс.
3. Построить перпендикуляр
в этой точке.
4. Отметить точки пересечения
перпендикуляра с окружностью.
-1
a
0
1
x
5. Полученные точки –
решение уравнения cosx = a.
6. Записать общее решение
уравнения.
-x1
х х1 2 n , n Z
содержание

4. Частные случаи уравнения cosх = a

cosx = 1
π
y 2
х 2 n , n Z
cosx = 0
π
-1
0
0
1
x
x
2
n, n Z
cosx = -1
π
2
x 2 n, n Z
содержание

5. Уравнение sinx = a

1. Проверить условие | a | ≤ 1
y
1
π-х1
2. Отметить точку а на оси
ординат.
3. Построить перпендикуляр в
этой точке.
х1
a
0
x
4. Отметить точки пересечения
перпендикуляра с окружностью.
5. Полученные точки – решение
уравнения sinx= a.
6. Записать общее решение
уравнения.
-1
х1 2 n , n Z
х
x1 2 n , n Z
содержание

6. Частные случаи уравнения sinх = a

sinх = 1
π
y 2
х
1
2
2 n , n Z
sinх = 0
π
0
x
0
х n , n Z
sinх = -1
-1
π
2
х
2
2 n , n Z
содержание

7. Примеры уравнений

y
3
1
cos x
2
х
-1
0
1 x
1
2
3
2 n , n Z
3
содержание

8. Примеры уравнений

y
5
6
6
1
2
-1
0
1 x
1
sin x
2
6 2 n , n Z
х
5 2 n , n Z
6
содержание