Similar presentations:
Экономическая оценка инвестиционного проекта
1. Чистая приведенная стоимость
TЧПС ( R (t ) З (t )) (1 e)
t 1
t p t
,
2. Чистая приведенная стоимость
ЧПСT
(( R1(t ) R2 (t ) R3 (t ) R4 (t ))
t 1
( З1 (t ) З 2 (t ) З 3 (t ) З 4 (t )) (1 e)
t p t
,
3. Чистая приведенная стоимость
TЧПС ( Ri (t ) З i (t )) (1 e)
t 1
t p t
i
4.
• R (t), R (t), R (t), R (t), - выраженные втекущих ценах результаты в году t,
соответственно для инвестора (индекс
1), разработчика (2), предприятия (3) и
государства (4);
• З1 (t ), З2 (t ), З3 (t ), З4 (t ) - выраженные в
текущих ценах затраты в году t для
соответствующих участников проекта;
1
2
3
4
5. Метод фактора аннуитета.
Пусть инвестиции осуществляютсяодин раз в году t=0, доходы и
расходы по годам не меняются,
6. Метод фактора аннуитета
ЧПСT
K i ( Ri C i ) (1 e)
t
t 1 i
i
T
K i ( Ri C i ) (1 e) K i ( Ri C i ) A .
i
i
t 1
t
i
i
7. А –текущая стоимость фактора аннуитета
TA (1 e)
t 1
t
,
8.
1А
е
1
Т
1
(1 е)
9. Пример 1.
• Пусть имеется 4 варианта (j) вложенияинвестиций в разные технологии,
ежегодные доходы R i (i = 1 - инвестор, i
= 2 - разработчик, i = 3 - предприятие, i
= 4 - государство), эксплуатационные
расходы C K - разовые вложения в
году t = 0. Для простоты расчетов
примем, что жизненный цикл проектов
равен 8 лет, а норма дисконтирования e
= 0,14.
i
i
10.
• Определить чистую приведеннуюстоимость по вариантам и выявить
наиболее выгодный
11.
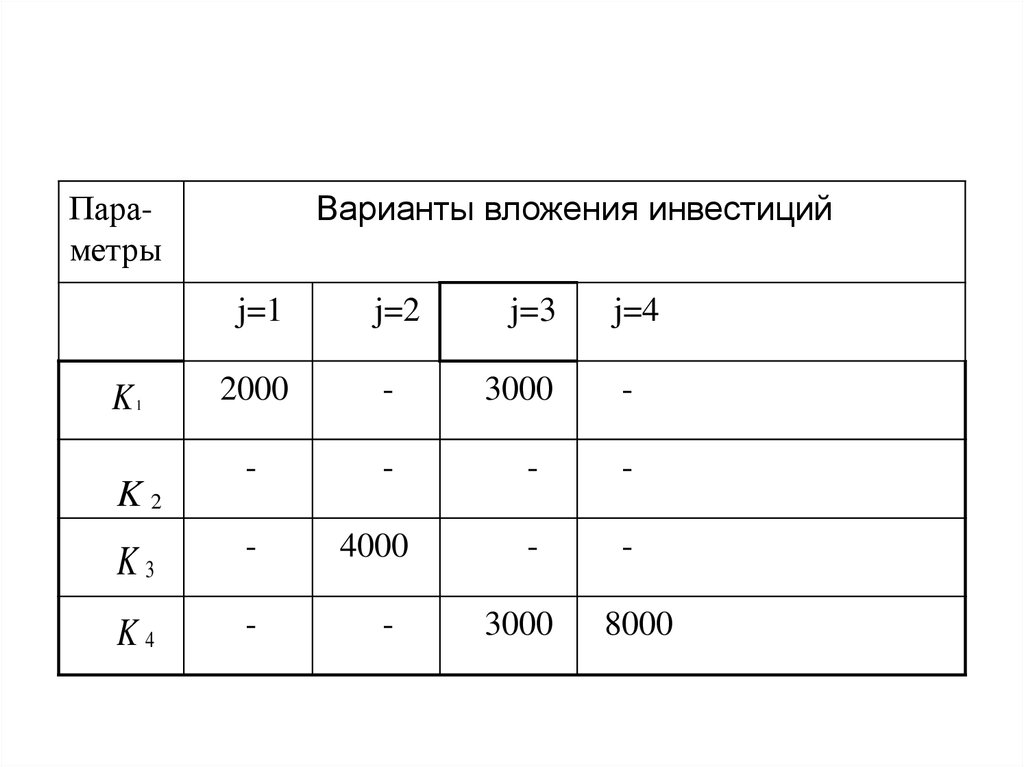
Варианты вложения инвестицийПараметры
K
1
K2
j=1
j=2
2000
-
-
-
K3
-
K4
-
4000
-
j=3
3000
j=4
-
-
-
-
-
3000
8000
12.
ПараметрыВарианты вложений
инвестиций
j=1
200
R1
R2
j=2
-
-R
j=3
4
-
R4
j=4
600
-
500
R3
480
1500
800
1500
R4
320
500
600
2000
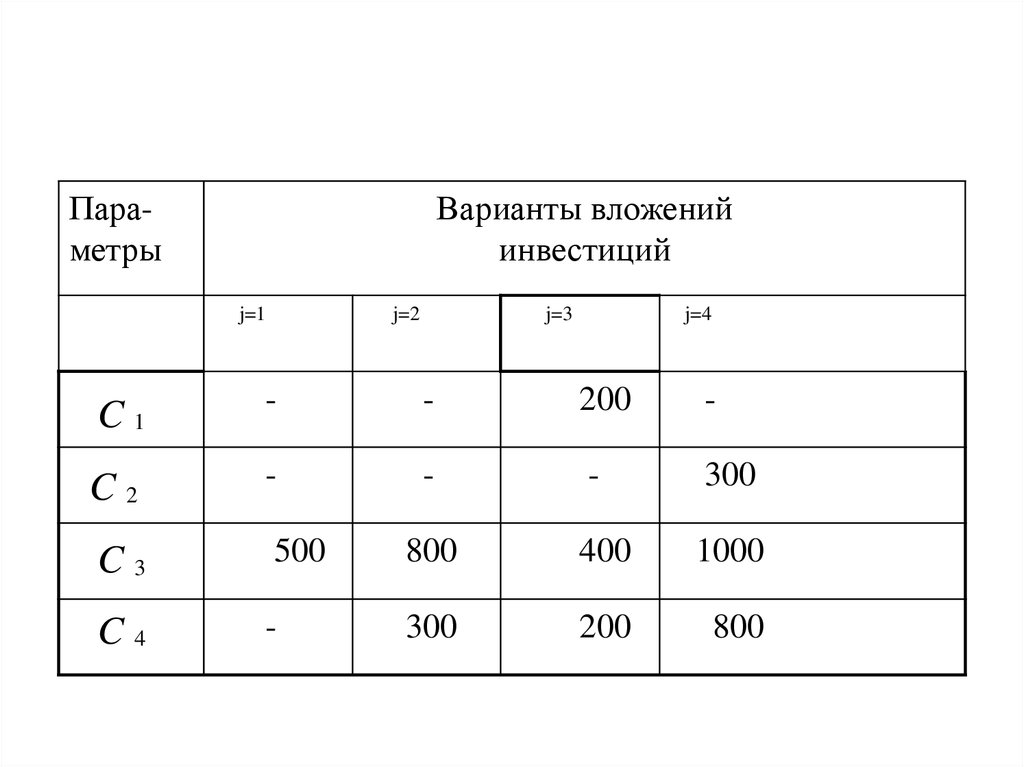
13.
ПараметрыВарианты вложений
инвестиций
j=1
j=2
j=3
j=4
C1
-
-
200
-
C2
-
-
-
300
C3
500
800
400
1000
C4
-
300
200
800
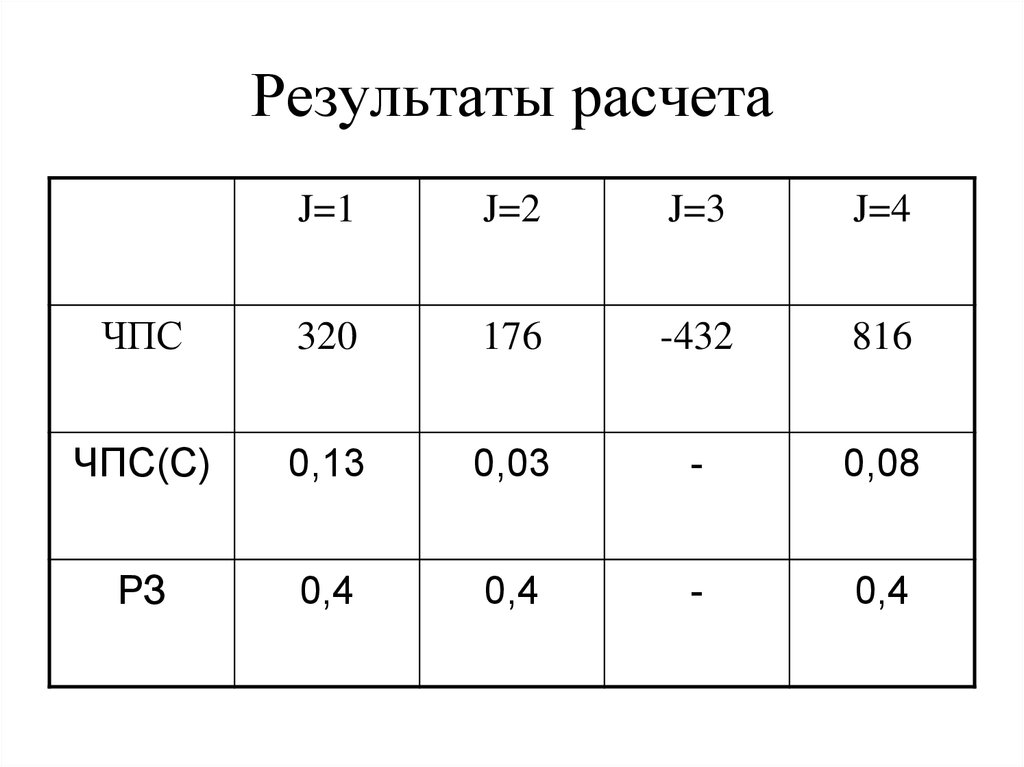
14. Результаты расчета
J=1J=2
J=3
J=4
ЧПС
320
176
-432
816
ЧПС(С)
0,13
0,03
-
0,08
РЗ
0,4
0,4
-
0,4
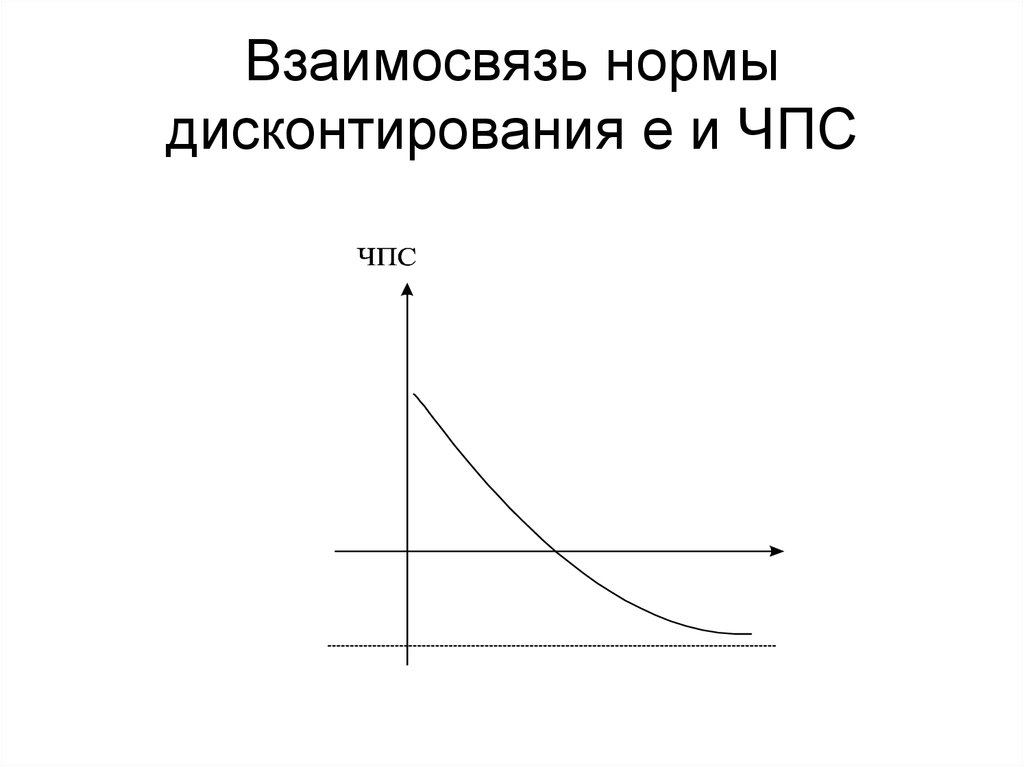
15. Внутренняя норма возврата (отдачи, доходности, прибыли)
Под внутренней нормой возвратапонимается такое значение нормы
дисконтирования, при которой чистая
приведенная стоимость равна нулю
(ЧПС(е)=0)
16. Взаимосвязь нормы дисконтирования e и ЧПС
17. Соотношение результатов и затрат (РЗ).
TРЗ
R (t ) (1 e)
t 1
T
t p t
i
i
З (t ) (1 e)
t 1
t p t
i
i
18. Соотношение чистой приведенной стоимости и затрат (ЧПС(С))
TЧПС(С )
( R (t ) З (t )) (1 e)
t 1
t p t
i
i
i
T
З (t ) (1 e)
t 1
t p t
i
i
19. Cрок возврата инвестиций.
Период времени, в течение которогопервоначальные инвестиционные
затраты компенсируются получаемыми
прибылями. Решается уравнение ЧПС (t ) 0
При этом определенный срок возврата
сопоставляется с некоторым
"стандартом" t .
вв
20. Точка безубыточности.
• Определяются пороговые значенияобъемов продаж продукции V, при
которых проект остается еще
прибыльным, т.е. выполняется условие
ЧПС(V) = 0. При этом все затраты
разделяются на постоянные (не
зависящие от объема продаж) и
переменные (пропорциональные
выпуску продукции).
21. Пример 2.
• Пусть рассматривается проект внедрениятехнологии в некоторую отрасль
промышленности. Примем, что разовые
инвестиции равны 5 млн.руб. Жизненный
цикл проекта 2 года. В первый год доход от
продажи составляет 28 млн.руб., а во второй
год производятся затраты, связанные с
экологическим восстановлением окружающей
среды в размере 28 млн.руб. Определить
внутреннюю норму возврата.
22.
(28 0) (0 28)5 (1 e)
(1 e)
2
2
28
x
5
0
28x
2
28
x
5
0
28x
0
23.
x1, 2
b
2
(b 4ac)
2a
24.
• X1=0,77• x2 =0,23







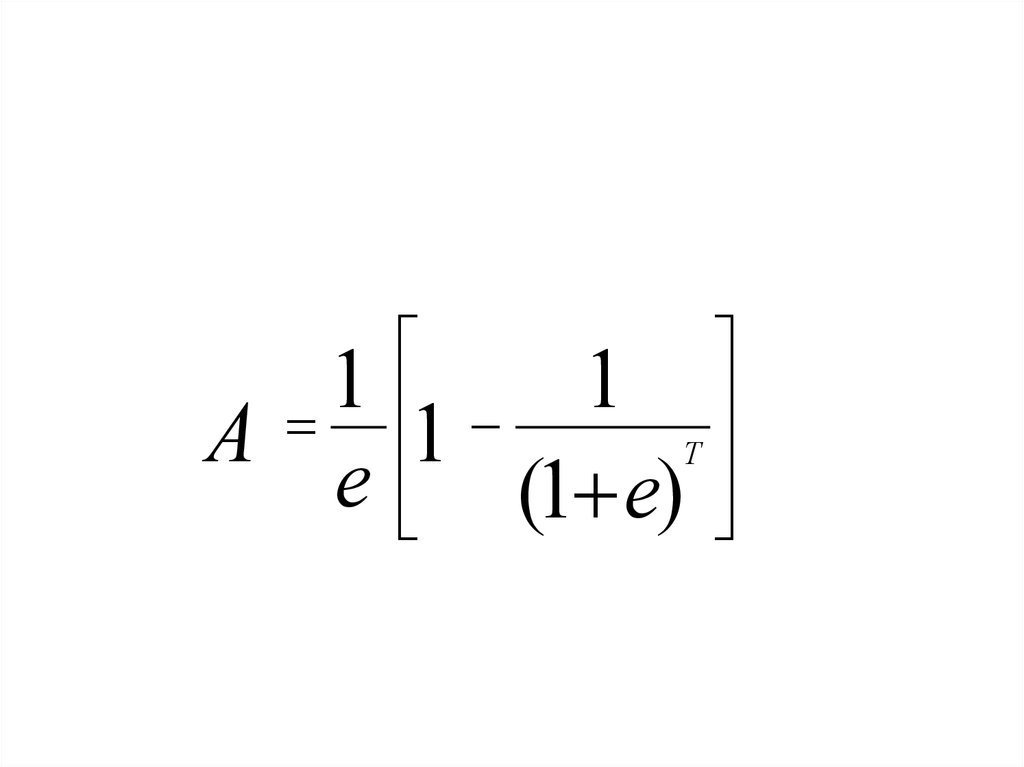









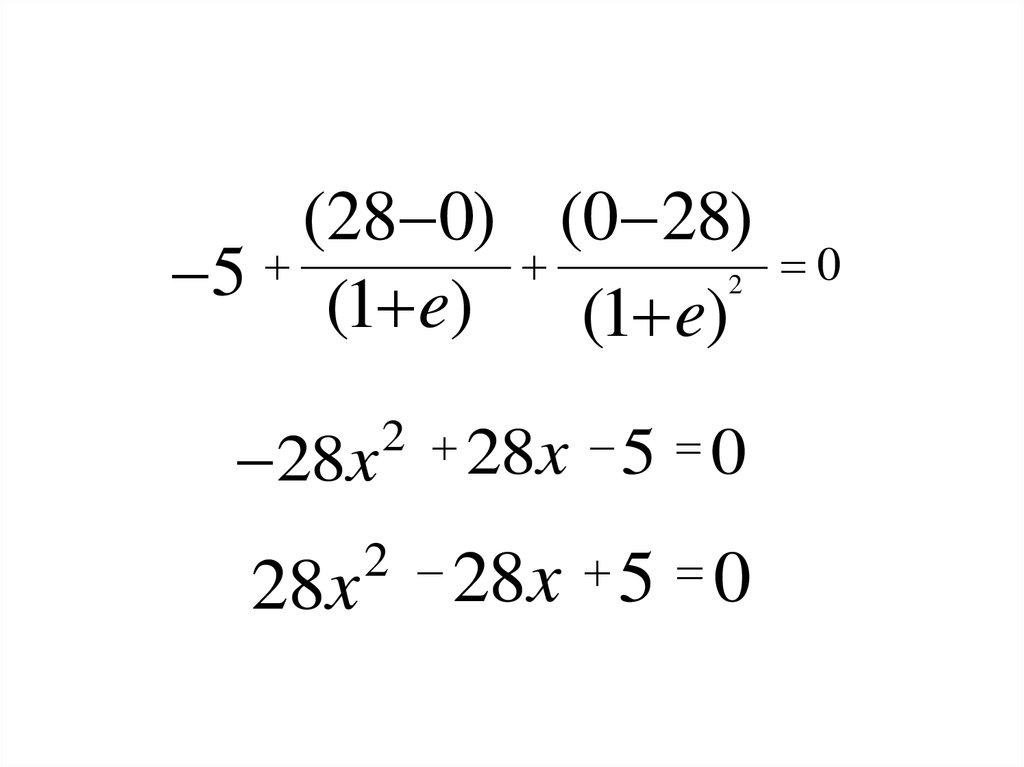


 finance
finance








