Элементы классической теории металлов. Недостатки электропроводности. (Лекция 9б)

1.

Кафедра физики
ЛЕКЦИЯ 9б
ПЛАН ЛЕКЦИИ
1. Элементы
классической
металлов. Недостатки.
теории
электропроводности
2. Равновесное состояние электронного газа в проводнике в
отсутствие электрического поля.
3. Дрейф электронов под действием внешнего электрического
поля.
4. Время релаксации, эффективная масса и длина свободного
пробега электрона.
5. Электропроводность вырожденного электронного газа.
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
1

2.

Кафедра физики
ЭЛЕМЕНТЫ КЛАССИЧЕСКОЙ ТЕОРИИ
ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ. НЕДОСТАТКИ.
Высокая электрическая проводимость металлов обусловлена
большой концентрацией электронов проводимости, которые и
являются носителями тока.
В классической теории электроны проводимости рассматриваются
как электронный газ, обладающий свойствами идеального
одноатомного газа.
Основные положения классической теории электропроводности
металлов следующие.
1. В отсутствие электрического поля электроны проводимости
хаотически движутся и сталкиваются с ионами металла. Ионы
колеблются около положений равновесия – узлов кристаллической
решетки. Электроны имеют одинаковую по модулю среднюю
скорость теплового движения u . Их средняя длина свободного
пробега порядка расстояния между узлами решетки металла.
2. Ток в металле возникает под действием электрического поля,
которое вызывает дрейф электронов.
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
2

3.

Кафедра физики
ЭЛЕМЕНТЫ КЛАССИЧЕСКОЙ ТЕОРИИ
ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ. НЕДОСТАТКИ.
Плотность тока
j n0 e v
где
n0 - концентрация электронов проводимости; v - средняя
скорость дрейфа электронов.
Оценки: средняя скорость v << средней скорости теплового
движения электронов u . Это объясняется малой средней длиной
свободного пробега электронов между двумя последовательными
столкновениями с ионами металла.
3. Предполагается, что при соударениях с ионами электроны
полностью теряют скорость упорядоченного движения.
Из этого предположения оценивается средняя скорость
упорядоченного
движения
электронов
под
действием
электрического поля и плотность тока проводимости в металле:
n0 e 2
j
E
2 m u
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
3

4.

Кафедра физики
ЭЛЕМЕНТЫ КЛАССИЧЕСКОЙ ТЕОРИИ
ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ. НЕДОСТАТКИ.
j n0 e 2
E
2 m u
Величину
называют удельной электрической проводимостью, а обратную ей
величину – удельным электрическим сопротивлением проводника.
j E
1
E,
или в векторной форме:
1
j E E
Это закон Ома в дифференциальной форме.
4. При соударениях с ионами кристаллической решетки электроны
теряют скорость. Энергия упорядоченного движения электронов
преобразуется во внутреннюю энергию проводника. Проводник
нагревается.
Объемная плотность тепловой мощности тока w выражается законом
Джоуля –Ленца.
В дифференциальной форме этот закон имеет вид:
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
w E 2
4

5.

Кафедра физики
ЭЛЕМЕНТЫ КЛАССИЧЕСКОЙ ТЕОРИИ
ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ. НЕДОСТАТКИ.
Недостатки классической теории:
Классическая
теория
электропроводности
металлов
чрезвычайно упрощенной и не давала объяснения
экспериментальных фактов.
была
ряду
Например:
А). Экспериментами установлено, что в довольно широком
интервале температур Т удельное электрическое сопротивление .
пропорционально Т, а удельная электрическая проводимость .
обратно пропорциональна Т.
Однако из формулы для и следует, что ~ 1 T и ~ T.
Попытки использовать классическое распределение вместо
допущения о том, что электроны имеют одинаковую среднюю
скорость теплового движения, существенного вклада в теорию не
дали.
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
5

6.

Кафедра физики
ЭЛЕМЕНТЫ КЛАССИЧЕСКОЙ ТЕОРИИ
ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ. НЕДОСТАТКИ.
Б). Удельную электрическую проводимость металла несложно
определить экспериментально.
Для того чтобы получить в расчетах значения , близкие к
экспериментальным, приходилось предполагать, что электрон
проходит без соударений с ионами решетки сотни межузельных
расстояний, что не совпадает с классической теорией.
Возникали и иные противоречия между экспериментом и теорией, из
которых следовало, что просто уточнениями существующей теории
электропроводности металлов затруднения не будут устранены.
Требовалась качественно новая теория.
Такой теорией явилась квантовая электронная теория металлов,
разработанная А.Зоммерфельдом в 1928 году.
Зоммерфельд применил к электронному газу в металле не
классическую статистику Максвелла – Больцмана, а квантовую
статистику Ферми – Дирака.
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
6

7.

Кафедра физики
РАВНОВЕСНОЕ СОСТОЯНИЕ ЭЛЕКТРОННОГО ГАЗА В
ПРОВОДНИКЕ В ОТСУТСТВИЕ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
В квантовой теории, как и в классической, утверждается, что
электропроводность металла обусловлена наличием свободных
электронов или электронов проводимости.
Практически в любых условиях, в которых находится проводник,
свободные электроны являются вырожденными.
Состояние вырожденных электронов в металле описывается
моделью потенциального «ящика» или потенциальной ямы.
Эта яма имеет вертикальные стенки, в ней нет электрического поля,
объем ямы эквипотенциален.
В потенциальной яме электроны стремятся занять наиболее
устойчивые энергетические уровни, начиная от дна. Работу выхода
электрона нужно отсчитывать от верхнего из занятых электронами
энергетического уровня.
Вспомним, что этим уровнем является уровень Ферми.
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
7

8.

Кафедра физики
РАВНОВЕСНОЕ СОСТОЯНИЕ ЭЛЕКТРОННОГО ГАЗА В
ПРОВОДНИКЕ В ОТСУТСТВИЕ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
В отсутствие электрического поля электронный газ в металле
находится в равновесном состоянии и описывается равновесной
функцией распределения.
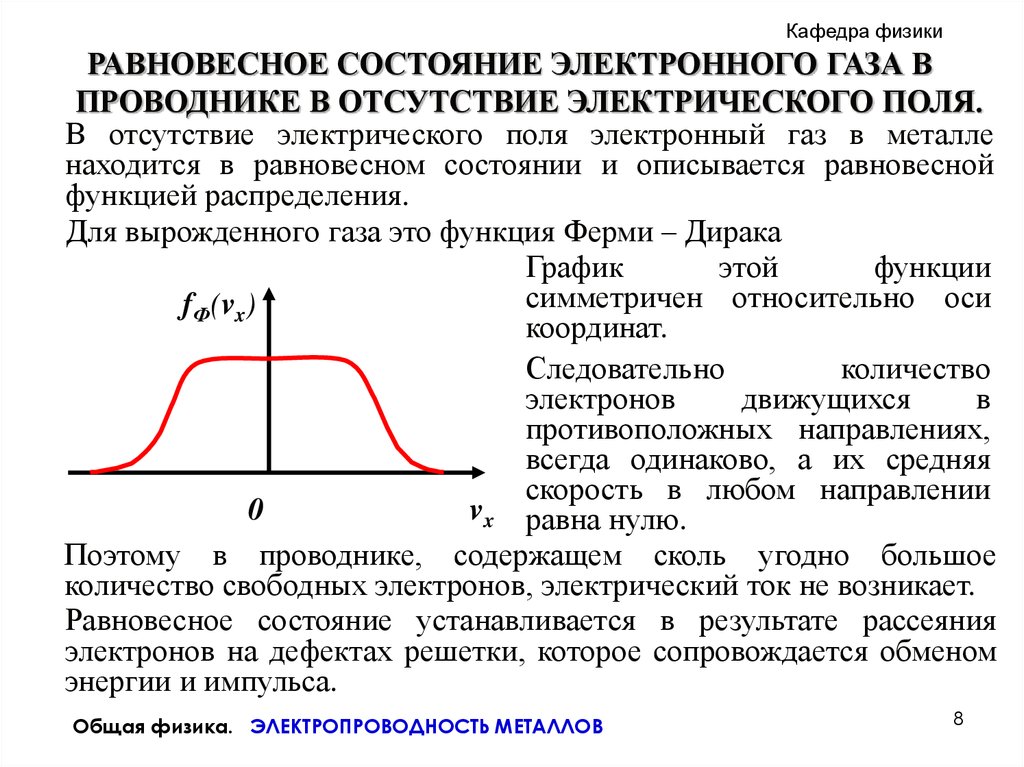
Для вырожденного газа это функция Ферми – Дирака
График
этой
функции
симметричен относительно оси
fФ(vx)
координат.
Следовательно
количество
электронов
движущихся
в
противоположных направлениях,
всегда одинаково, а их средняя
скорость в любом направлении
vx равна нулю.
0
Поэтому в проводнике, содержащем сколь угодно большое
количество свободных электронов, электрический ток не возникает.
Равновесное состояние устанавливается в результате рассеяния
электронов на дефектах решетки, которое сопровождается обменом
энергии и импульса.
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
8

9.

Кафедра физики
ДРЕЙФ ЭЛЕКТРОНОВ ПОД ДЕЙСТВИЕМ ВНЕШНЕГО
ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
При приложении к проводнику электрического поля в нем возникает
ток.
Возникновение тока в проводнике свидетельствует о том, что под
действием поля электроны приобретают направленное
движение.
Сила, действующая на электрон со стороны поля E , равна F eE.
Под действием этой силы электрон должен был бы двигаться
ускоренно, и его скорость должна была бы непрерывно нарастать.
Однако при своем движении электрон сталкивается с дефектами
решетки и, рассеиваясь, теряет скорость.
Действие решетки
можно формально свести к действию силы
сопротивления Fc , которую испытывает электрон при своем
движении через решетку.
Эта сила пропорциональна скорости дрейфа электрона v д и
направлена противоположно ей:
1 *
Fc m v д
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
9

10.

Кафедра физики
ДРЕЙФ ЭЛЕКТРОНОВ ПОД ДЕЙСТВИЕМ ВНЕШНЕГО
ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
1 *
Fc m v д
- время релаксации (характеризует скорость установления в
системе равновесного состояния);
m* - эффективная масса электрона.
Теперь можно записать II закон Ньютона в виде:
1 *
d
v
t
*
д
m
F Fc eE m v д t
dt
Видно, что после включения поля скорость v д t будет возрастать, и
электроны будут
двигаться ускоренно до тех пор, пока сила
сопротивления Fc , пропорциональная скорости v д t , не окажется
равной силе, действующей со стороны поля.
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
10

11.

Кафедра физики
ДРЕЙФ ЭЛЕКТРОНОВ ПОД ДЕЙСТВИЕМ ВНЕШНЕГО
ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
Когда эти силы сравняются, действующая на электрон
результирующая сила будет равна нулю.
eE
Начиная с этого момента, электрон будет
vд *
двигаться с постоянной скоростью:
m
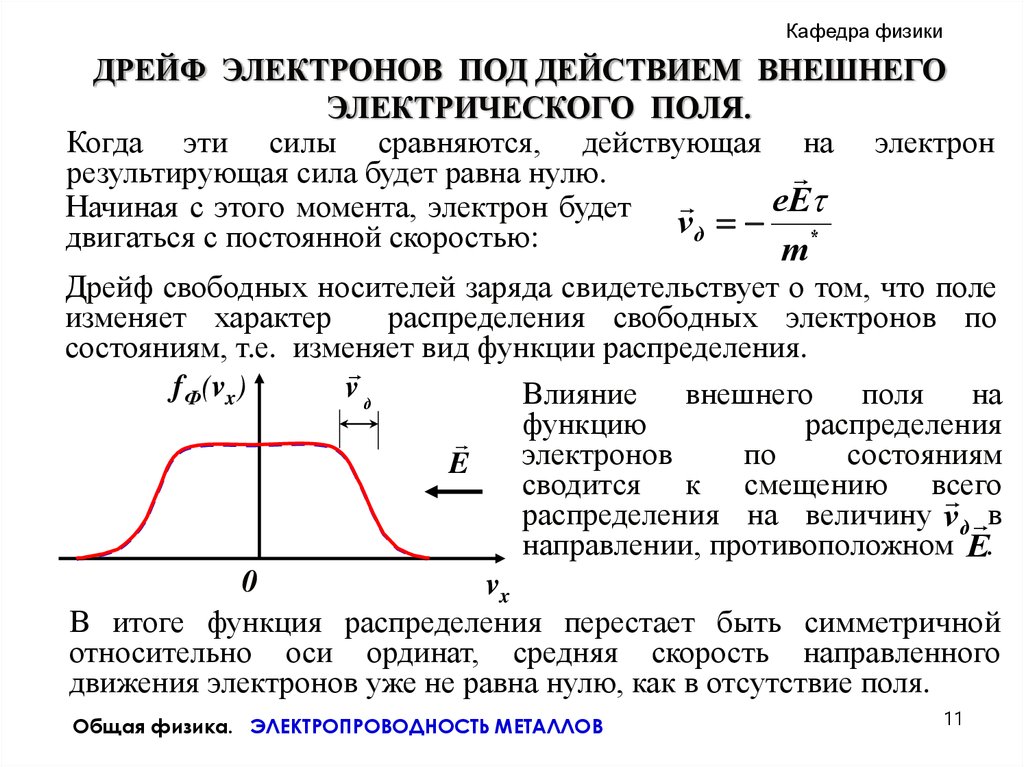
Дрейф свободных носителей заряда свидетельствует о том, что поле
изменяет характер
распределения свободных электронов по
состояниям, т.е. изменяет вид функции распределения.
fФ(vx)
vд
Влияние
внешнего
поля
на
функцию
распределения
электронов
по
состояниям
E
сводится к смещению всего
распределения на величину v д в
направлении, противоположном E.
0
vx
В итоге функция распределения перестает быть симметричной
относительно оси ординат, средняя скорость направленного
движения электронов уже не равна нулю, как в отсутствие поля.
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
11

12.

Кафедра физики
ДРЕЙФ ЭЛЕКТРОНОВ ПОД ДЕЙСТВИЕМ ВНЕШНЕГО
ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
Итак, при постоянной напряженности E электрического поля
скорость дрейфа достигает постоянного значения.
Это возможно лишь в случае, если сила, с которой электрическое
поле действует на электрон, компенсируется силой Fc .
В противном случае скорость дрейфа непрерывно росла бы и даже
при небольших полях могла бы стать сколь угодно большой.
Электропроводность в этом случае была бы бесконечной, а
электрическое сопротивление равнялось бы нулю.
Как показывают квантово-механические расчеты, такая ситуация
была бы возможна в случае идеальной кристаллической решетки.
Электроны проводимости не испытывали бы при своем движении
никакого сопротивления и электропроводность металлов была бы
бесконечно большой.
Однако кристаллическая решетка никогда не бывает совершенной.
Из-за наличия примесей или вакансий (отсутствия атомов в узле)
происходит рассеяние электронов и проводимость оказывается
конечной.
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
12

13.

Кафедра физики
ВРЕМЯ РЕЛАКСАЦИИ, ЭФФЕКТИВНАЯ МАССА И
ДЛИНА СВОБОДНОГО ПРОБЕГА ЭЛЕКТРОНА.
Рассмотрим физический смысл параметров и m* - времени
релаксации и эффективной массы электрона.
Разберемся также с длиной свободного пробега электрона в
кристалле.
Предположим, что после того, как скорость направленного
движения
электронов достигла стационарного значения v д , электрическое поле
выключили.
Положив в уравнении II закона Ньютона Е=0, получим:
dv д t 1
v д t 0
dt
Решение такого уравнения известно и имеет вид:
v д t v д 0 exp t
где v д 0 - значение дрейфовой скорости в момент выключения поля.
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
13

14.

Кафедра физики
ВРЕМЯ РЕЛАКСАЦИИ, ЭФФЕКТИВНАЯ МАССА И
ДЛИНА СВОБОДНОГО ПРОБЕГА ЭЛЕКТРОНА.
v д t v д 0 exp t
Из этого уравнения следует, что за время значение дрейфовой
скорости уменьшится в е раз.
Таким образом,
- это время, характеризующее процесс
установления равновесия между электронами и решеткой,
нарушенного действием внешнего поля Е.
Параметр m* - эффективная масса электрона – приписывается
электрону, находящемуся в периодическом поле кристалла.
С введением этой массы можно считать электрон свободным и
описывать его движение во внешнем поле так, как описывается
движение обычного свободного электрона.
Эффективная масса может сильно отличаться от фактической массы
электрона, в частности она может быть отрицательной.
По абсолютному значению она может быть как во много раз больше,
так и во много раз меньше массы покоя электрона.
Лишь свободный электрон имеет m*, равную массе покоя.
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
14

15.

Кафедра физики
ВРЕМЯ РЕЛАКСАЦИИ, ЭФФЕКТИВНАЯ МАССА И
ДЛИНА СВОБОДНОГО ПРОБЕГА ЭЛЕКТРОНА.
Эффективную массу электрона, заключающую в себе всю
особенность, присущую движению электрона в поле кристалла,
можно вычислить по формуле:
2
m* 2
d dk 2
где - энергия, которой обладает электрон в кристалле, k - волновое
число.
Таким образом, использование приближения свободных электронов
при рассмотрении движения электронов в периодическом поле
может считаться корректным лишь в том случае, если вместо
истинной массы учитывать эффективную массу электрона.
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
15

16.

Кафедра физики
ВРЕМЯ РЕЛАКСАЦИИ, ЭФФЕКТИВНАЯ МАССА И
ДЛИНА СВОБОДНОГО ПРОБЕГА ЭЛЕКТРОНА.
Движение электрона в кристалле удобно описывать, используя
понятие длины свободного пробега электрона.
Если бы электрон, как в классической теории, полностью терял
скорость упорядоченного движения уже в единичном акте рассеяния,
то средняя длина свободного пробега равнялась бы просто
произведению средней скорости электронов u
на время
свободного движения электрона.
Однако чаще для полного уничтожения направленной скорости
требуется не одно, а в среднем (ню) столкновений.
Тогда средний путь L , который пройдет электрон до полной
потери скорости упорядоченного движения, равен
u
L u
Величина L называется транспортной длиной свободного пробега.
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
16

17.

Кафедра физики
ЭЛЕКТРОПРОВОДНОСТЬ ВЫРОЖДЕННОГО
ЭЛЕКТРОННОГО ГАЗА.
Вспомним, что для вырожденного газа все состояния с энергией,
меньшей энергии Ферми, заняты электронами.
Внешнее поле может воздействовать только на электроны,
расположенные вблизи уровня Ферми, переводя их на более высокие
свободные уровни.
Следовательно, только эти электроны могут участвовать в
формировании электропроводности.
Учитывая это, запишем
выражение для установившейся
плотности тока:
e 2 E ф
j n0 e v д n0
m*
где ф - время релаксации электронов с энергией, практически
равной энергии Ферми.
ф ф ф uф ,
j n0
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
e E ф ф
2
m* uф
17

18.

Кафедра физики
ЭЛЕКТРОПРОВОДНОСТЬ ВЫРОЖДЕННОГО
ЭЛЕКТРОННОГО ГАЗА.
j n0
e E ф ф
2
ф -
*
m uф
Выражение для проводимости: n0
e 2 ф ф
m* uф
средняя длина свободного пробега электронов,
обладающих энергией Ферми,
uф - их скорость, ф - число
столкновений, в результате которых уничтожается направленная
скорость этих электронов.
Итак, основные принципиальные различия в формулах для
проводимости (классическая и квантовая теории):
n0 e 2
2 m u
n0
e 2 ф ф
m* uф
Внешний вид формулы для напоминает классическую формулу, но
физический смысл величин в формулах совершенно разный.
В классической формуле u - это средняя скорость
движения электронов, пропорциональная Т.
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
теплового
18

19.

Кафедра физики
ЭЛЕКТРОПРОВОДНОСТЬ ВЫРОЖДЕННОГО
ЭЛЕКТРОННОГО ГАЗА.
n0 e 2
2 m u
В квантовой
температуры.
n0
e 2 ф ф
m* uф
uф - это скорость, практически не зависящая от
В *классической формуле m - это масса покоя электрона, в квантовой
.m - это эффективная масса электрона.
Принципиально различен и смысл параметров и ф .
Из анализа следует, что длина свободного пробега электронов,
обусловленная рассеянием на тепловых колебаниях решетки,
обратно пропорциональна абсолютной температуре проводника.
Следовательно, ~ 1 T , что совпадает с опытными результатами.
Таким образом, квантовая теория электропроводности металлов
устраняет практически все противоречия, между теорией и
практикой, которые возникают в классической теории.
Общая физика. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
19