Similar presentations:
Моделирование взаимодействия процессов
1. Моделирование взаимодействия процессов.
Лекция 102. Параллельное программирование
• В настоящее время производительностьпроцессоров (точнее, их отдельных ядер)
приблизилась к своему физическому пределу
• Поэтому обеспечить дальнейшее повышение
вычислительных мощностей можно лишь за
счет увеличения их количества
• В связи с этим основной тенденцией
современного программирования становится
разработка параллельных программ
3. Способы реализации параллельных вычислений
• Каждый вычислительный процесс можетбыть реализован:
– в виде отдельного процесса операционной
системы,
– в виде отдельного потока выполнения внутри
одного процесса ОС
4. Способы реализации параллельных вычислений
• Параллельные программы могут физическиисполняться:
– последовательно на
единственном процессоре — перемежая по
очереди шаги выполнения каждого
вычислительного процесса;
– параллельно с выделением каждому
вычислительному процессу одного или
нескольких процессорных ядер
5. Синхронизация параллельных процессов
• При проектировании параллельныхпрограмм важно обеспечить правильную
последовательность взаимодействий
между различными вычислительными
процессами, а также координацию в
использовании разделяемых ими ресурсов
• Эта задача называется синхронизацией
параллельных процессов
6. Моделирование сетями Петри
• Сети Петри, изначально созданные длямоделирования динамических дискретных
систем, являются одним из наиболее
удобных способов описания асинхронного
выполнения параллельных вычислительных
процессов
7. Система с одним процессом
• Вырожденным случаем параллельнойсистемы вычислительных процессов
является система с одним процессом
• Сначала рассмотрим, как сетью Петри
может быть представлен отдельный
вычислительный процесс, описываемый
программой на одном из существующих
языков программирования
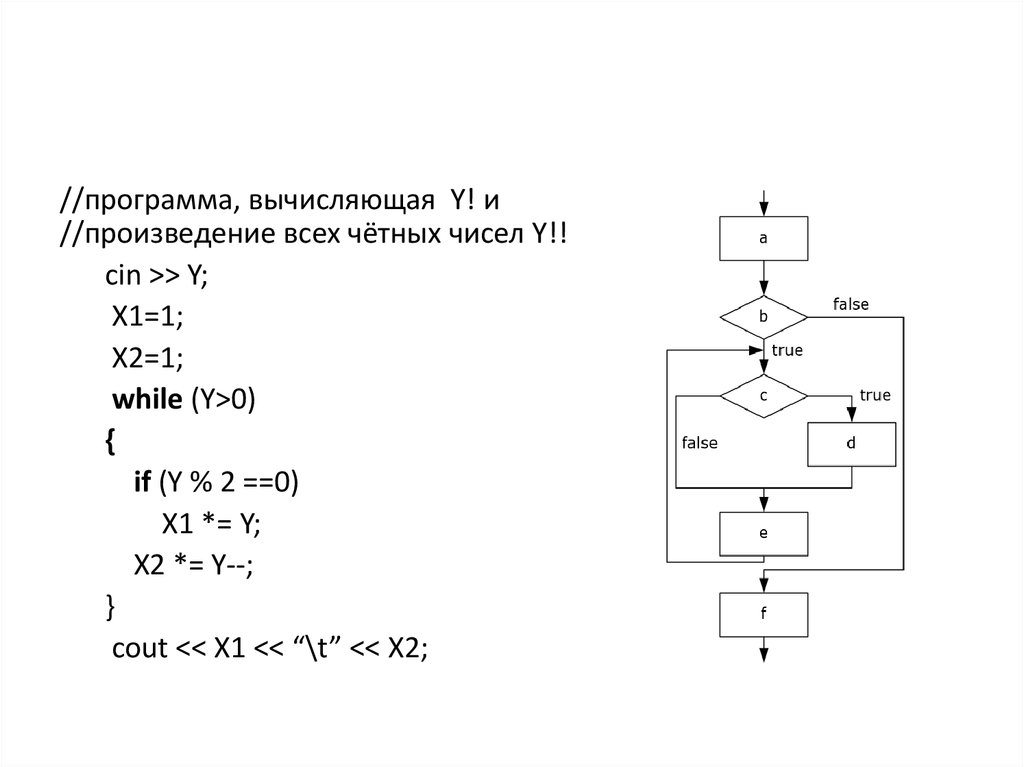
8.
//программа, вычисляющая Y! и//произведение всех чётных чисел Y!!
cin >> Y;
X1=1;
X2=1;
while (Y>0)
{
if (Y % 2 ==0)
X1 *= Y;
X2 *= Y--;
}
cout << X1 << “\t” << X2;
9.
a)b)
c)
d)
e)
f)
cin >> Y; X1=1; X2=1;
Y>0
Y % 2 ==0
X1 *= Y;
X2 *= Y--;
cout << X1 << “\t” <<
X2;
10.
• В сети Петри, моделирующей блок-схему,узлы блок-схемы представляются
переходами сети Петри, а дуги блок-схемы
– позициями сети Петри
• Фишка в сети Петри представляет счетчик
команд блок-схемы
11.
• Параллельная система может строитьсянесколькими способами
• Один из способов состоит в простом
объединении процессов, без
взаимодействия во время их
одновременного выполнения
• Однако, такой способ введения
параллелизма имеет низкое практическое
значение
12. Моделирование взаимодействия процессов
• Поэтому далее будем рассматривать системыпроцессов, допускающие взаимодействие
процессов во время их параллельного
выполнения
• Существуют различные виды взаимодействия
(синхронизации) процессов, в том числе:
взаимодействие посредством общей памяти;
посредством передачи сообщения различных
видов
• Необходимо уметь моделировать различные
механизмы синхронизации процессов
13. Задача о взаимном исключении
• Пусть несколько процессов разделяютобщую переменную, запись, файл или
другой элемент данных
• Если два процесса и в одно и то же время
пытаются изменить этот элемент данных, то
могут возникнуть нежелательные
искажения
14.
• Например, возможна следующаяпоследовательность:
– Процесс P1 считывает значение x из разделяемого
объекта;
– Процесс P2 считывает значение х из разделяемого
объекта;
– Процесс P1 вычисляет новое значение x’ = f(x);
– Процесс P2 вычисляет новое значение x’’ = g(x);
– Процесс P1 записывает x’ в разделяемый объект;
– Процесс P2 записывает x’’ в разделяемый объект,
уничтожая значение x’
• Результат вычисления процесса P1 потерян
15. Критическая секция
• Для решения подобных проблемиспользуется метод взаимного исключения,
основанный на понятии критическая
секция
• Критическая секция – это участок кода
процесса, на котором он осуществляет
доступ к разделяемому объекту данных
16.
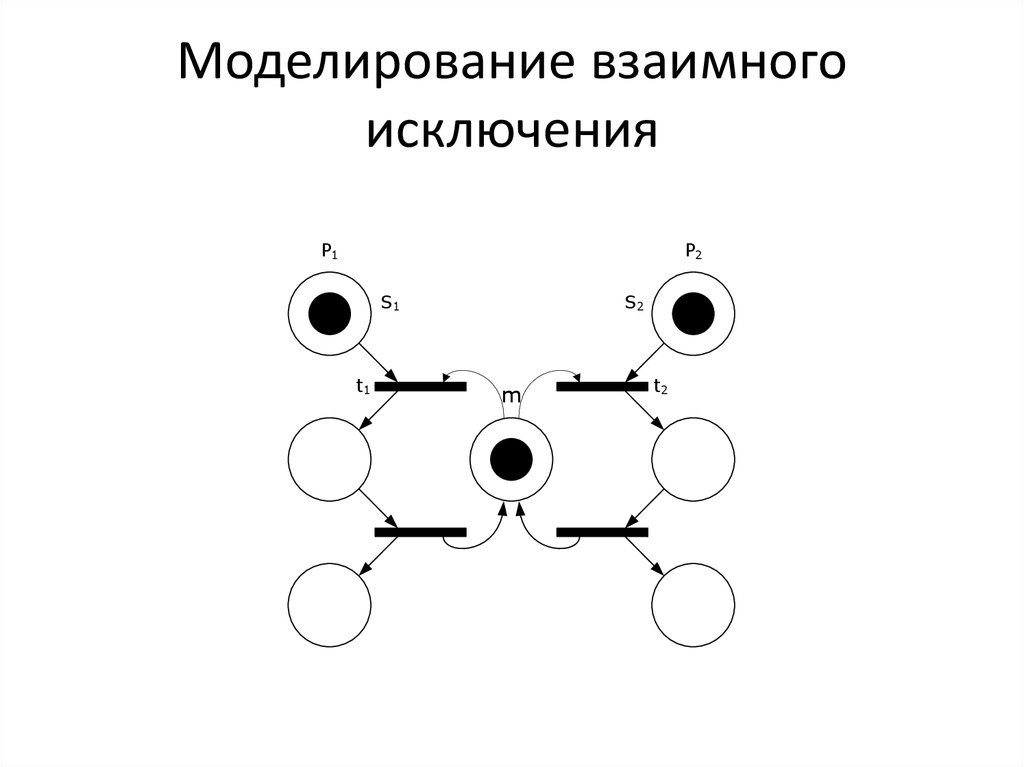
• Прежде, чем выполнить свою критическуюсекцию, процесс ждёт, пока другой процесс
не закончит выполнение собственной
критической секции и лишь затем он входит
в критическую секцию
• При этом блокируется доступ для любого
другого процесса к своей критической
секции до выхода этого процесса из
критической секции
17. Моделирование взаимного исключения
P1P2
S1
t1
S2
m
t2
18. Задача о производителе/потребителе
• В задаче о производителе/потребителе такжеприсутствует разделяемый объект – буфер,
посредством которого реализуется
взаимодействие через асинхронную передачу
сообщений
• Процесс-производитель создает сообщения,
которые помещаются в буфер
• Процесс-потребитель ждет, пока сообщение
не будет помещено в буфер, извлекает его
оттуда и использует
19. Моделирование буфера обмена
производительпроизвести
послать
в буфер
потребитель
B
извлечь
из буфера
использовать
20. Задача об обедающих философах
• В некоем пансионе нашли пристанище пятьфилософов. У каждого философа была своя
комната. Была у них и общая столовая с круглым
столом, вокруг которого стояли пять стульев.
• В центре стола стояла большая миска спагетти,
содержимое которой постоянно пополнялось. На
столе также лежало пять вилок, по одной между
соседними посадочными местами.
• Звали философов и за столом они располагались
в этом же порядке, против часовой стрелки.
Почувствовав голод, философ шёл в столовую,
садился на свой стул, брал сначала слева от себя
вилку, затем справа и приступал к еде. Закончив
трапезу, он клал на место обе вилки, выходил из-за
стола, и уходили размышлять
21. Проблема тупика
• В задаче об обедающих философах возможнаситуация, в которой каждый философ возьмет
вилку слева, а затем будет ждать, когда
освободится вилка с правой стороны
• Так они будут ждать, пока не умрут от голода
• Тем самым, это состояние системы
«обедающие философы» является тупиковым
22. Решение проблемы тупика
• Проблема тупика в этой системе можетбыть решена путем следующей
модификации ее правил поведения
• Пусть философ при переходе из состояния
размышления в состояние приема пищи
берет одновременно обе вилки (слева и
справа), если они свободны
23. Моделирование разрешения тупиковой ситуации
завjej
начj
пj
п1
дj
зав4
нач4
e4
д4
д1
e1
нач1
п4
п2
д3
д2
п3
нач3
нач2
e3
зав3
e2
зав2
зав1
24. Свойства сетей Петри
• Моделирование систем сетями Петри, преждевсего, обусловлено необходимостью
проведения глубокого исследования их
поведения
• Очевидно, что это предполагает наличие
методов анализа свойств самих сетей Петри
• Тем самым исследование свойств реальной
системы может быть сведено к анализу
определенных свойств моделирующей сети
Петри



























 programming
programming








