Тепломассообмен. Сложный теплообмен

1. ТЕПЛОМАССООБМЕН

Сложный теплообмен
Лекция № 4.2
2017 год

2. План

• 1. Критический диаметр изоляции.
• 2. Теплопередача
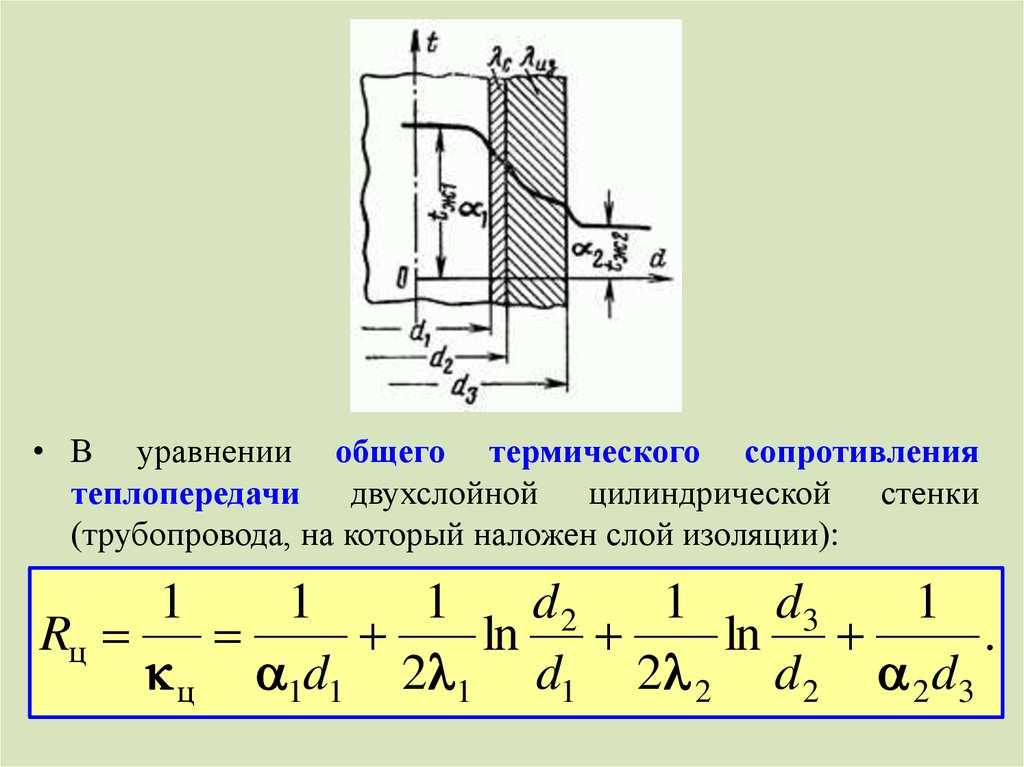
стенку.
• 3.
Способы
теплопередачи.
через
плоскую
интенсификации
ребристую
процессов

3. 1. Критический диаметр изоляции

Тепловой изоляцией называют всякое покрытие
горячей
поверхности,
которое
способствует
снижению потерь теплоты в окружающую среду.

4.

• Для тепловой изоляции используют любые
материалы с низкой теплопроводностью – асбест,
пробка, слюда, шлаковая или стеклянная вата, шерсть
и др.
• Анализ формулы полного линейного термического
сопротивления теплопередачи цилиндрической
стенки показывает, что тепловые потери
изолированных трубопроводов уменьшаются не
пропорционально
увеличению
толщины
изоляции.

5.

• При неправильном выборе материала изоляции тепловые
потери возрастут.
• Это связано с тем, что у изолированного трубопровода
внешняя поверхность увеличивается и условия теплоотвода
улучшаются.
• Анализ показывает, что материал выбран правильно, если λиз
удовлетворяет неравенству
2d2
из
,
2
• где d2 – наружный диаметр трубопровода, а α2, и –
коэффициент теплоотдачи от внешней поверхности к
окружающей среде.

6.

• Рассмотрим условие, при котором материал,
используемый для изоляции трубы, будет
уменьшать тепловые потери.
• Цилиндрическая
изоляцией.
труба
покрыта
однослойной
• При постоянных α1, α2, d1, d2, λ1, λ2, t1 и t2
рассмотрим,
как
будет
изменяться
полное
термическое сопротивление при изменении толщины
изоляции.

7.

• В уравнении общего термического сопротивления
теплопередачи двухслойной цилиндрической стенки
(трубопровода, на который наложен слой изоляции):
1
1
1
d2
1
d3
1
Rц
ln
ln
.
ц 1d1 2 1 d1 2 2 d 2 2 d3

8.

1
1
1
d2
1
d3
1
Rц
ln
ln
.
ц 1d1 2 1 d1 2 2 d 2 2 d3
• Из формулы следует, что при наложении изоляции
термическое сопротивление слоя изоляции возрастает на
величину
1
d
2 2
ln
3
d2
это способствует снижению потерь теплоты, но одновременно
термическое сопротивление теплоотдачи в окружающую среду
уменьшается на величину
1 1
1
2 d 2 d3
• что связано с увеличением внешней поверхности (d3>d2).

9.

1
1
d2
1
d3
1
Rц
ln
ln
.
1d1 2 1 d1 2 2 d 2 2 d3
• Возьмем первую производную от правой части уравнения по
d3 и приравнивая ее к нулю, получаем:
d Rц
1
1
0
.
2
d d3 2 2 d3 2 d3

10.

Критический
диаметр
изоляции,
отвечающий
экстремальной точке кривой
R f d3 ,
определяется формулой:
2 из
dкр dиз d 2
.
2
Из формулы следует: критический диаметр изоляции
не зависит от размеров трубопровода.

11.

2 из
d кр
.
2
Критический диаметр тем меньше, чем меньше
теплопроводность изоляции и чем больше теплоотдачи от
наружной поверхности изоляции к окружающей среде.
Если вторая производная от Rц больше нуля.
Следовательно, критический диаметр соответствует
минимуму теплового сопротивления и максимуму
теплового потока.

12.

Анализ уравнения
2 из
dкр
2
показывает, что если наружный диаметр изоляции dиз
увеличивается, но остается меньше dкр, то тепловые
потери возрастают и будут больше тепловых потерь
голого трубопровода (кривая АК).

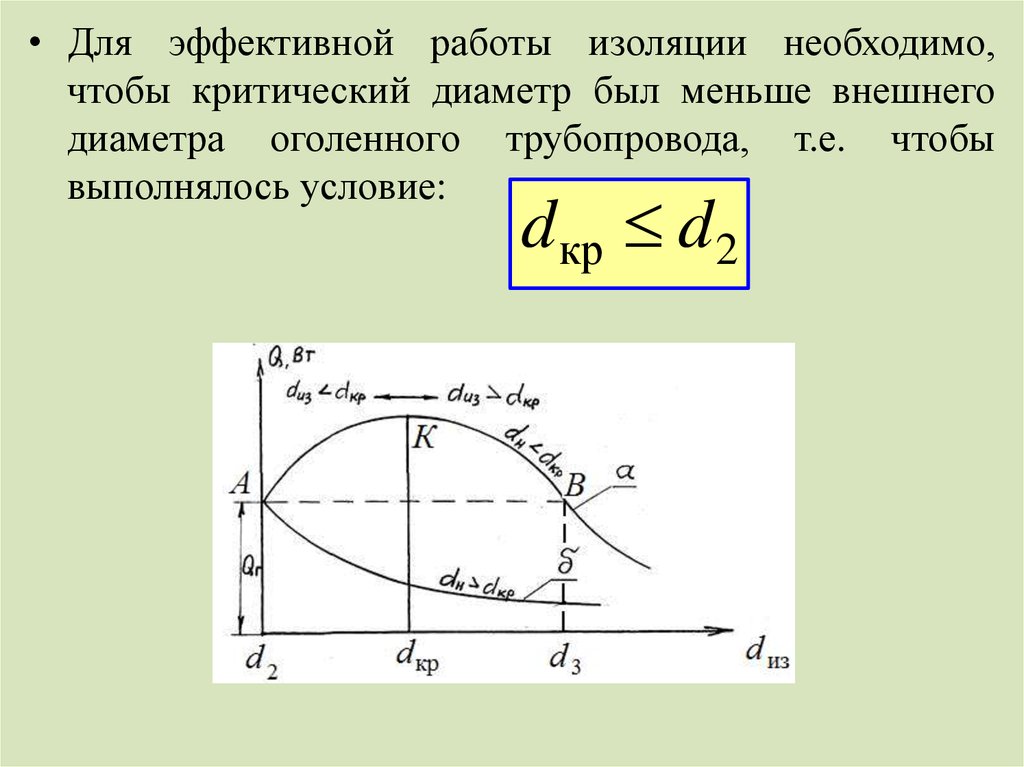
13.

При равенстве dиз=dкр получаются максимальные тепловые
потери в окружающую среду (точка К).
При дальнейшем увеличении наружного диаметра изоляции
dиз>dкр теплопотери будут меньше, чем при dиз=dкр (кривая
ВК).
Только при dиз=d3 тепловые потери вновь станут такими же,
как и для неизолированного трубопровода.

14.

• Для эффективной работы изоляции необходимо,
чтобы критический диаметр был меньше внешнего
диаметра оголенного трубопровода, т.е. чтобы
выполнялось условие:
dкр d 2

15.

• Для того чтобы изоляция вызывала уменьшение
теплопотерь цилиндрической стенки по сравнению с
голым трубопроводом, при данном наружном
диаметре трубы d2 и заданным коэффициентом
теплоотдачи α2 необходимо, чтобы
2d2
из
.
2

16.

Характер изменения тепловых потерь
трубопровода ql в зависимости от
толщены слоя из 0,5 d3 d 2 при
рациональном и неверном подборе
материала показан на рисунке

17. Пример

• Для изоляции трубопровода диаметром d2= 30 мм
имеется шлаковая вата, теплопроводность которой
λиз= 0,1 Вт/(м·К), коэффициент теплоотдачи α2= 4,0
Вт/(м2·К).
• Целесообразно ли применять в данном случае в
качестве изоляции шлаковую вату?

18. Пример

• Критический диаметр изоляции
2 из 2 0,1
d кр
0,05 м 50 мм.
2
4
Так как dкр>d2, шлаковую вату в рассматриваемом
случае применять нецелесообразно.
• Для нашей задачи λиз должна быть меньше
2 d 2 4 0,03
Вт
из
0,06
.
2
2
м К

19. 2. Теплопередача через плоскую ребристую стенку

Ребристые поверхности применяются для выравнивания
термических сопротивлений теплоотдачи с обеих сторон стенки,
когда одна поверхность омывается капельной жидкостью с
большим коэффициентом теплоотдачи, а другая поверхность
омывается газом с малым коэффициентом теплоотдачи,
создающим большое термическое сопротивление.

20.

• Оребрение стенки с большим
сопротивлением позволяет:
термическим
увеличить ее поверхность соприкосновения с
горячим (или холодным) теплоносителем;
уменьшить общее
теплопередачи;
тепловое
увеличить тепловые потоки.
сопротивление

21.

• Температура ребер изменяется по высоте, если t1>t2.
• У основания ребра температура равна температуре
поверхности стенки t 'ст .
• У вершины ребра температура будет значительно
меньше и равна t"ст .
• Участки поверхности ребра у основания передают
больше теплоты, чем участки у ребра вершины.

22.

• Отношение
количества
теплоты
QTр,
передаваемой поверхностью ребер в окружающую
среду, к теплоте QTп.р., которую эта поверхность
могла передать при постоянной температуре,
равной температуре у основания ребер, называется
коэффициентом эффективности ребер:
э
QTр
QTп.р.
• Коэффициент эффективности
меньше единицы.
ребер
всегда
Для коротких ребер, выполненных из материала с высокой
теплопроводностью, коэффициент эффективности близок к
единице.

23.

Рассмотрим плоскую стенку толщиной δ, на одной
стороне которой имеются ребра.
Температура гладкой поверхности
ребер и простенков между ними
принимается
в
первом
приближении равной постоянной
величине t"ст .
Стенка и ребра выполнены из
одного материала с высокой
теплопроводностью λ.

24.

• Коэффициент теплоотдачи на гладкой
стороне α1.
• Коэффициент теплоотдачи ребер α2.
• Площадь гладкой поверхности F1.
• Площадь
поверхности
ребер
промежутков между ними F2.
и
• Температура горячего теплоносителя
t1.
• Температура холодного теплоносителя
t2.

25.

• Для стационарного режима можно записать три
уравнения теплового потока:
Q 1F1 t1 t 'ст ,
Q F1 t 'ст t"ст ,
Q 2 F2 t"ст t2 .

26.

• Решая уравнения относительно
складывая, получаем:
Q
• или
разности
t1 t2
1
1
1F1 F1 2 F2
температур
,
Q р t1 t2 ,
где κр – коэффициент теплопередачи для ребристой стенки.
Вт
р 1 .
К
и

27.

• коэффициент теплопередачи для ребристой стенки
1
р
,
1
1
1F1 F1 2 F2

28.

• Тепловой поток отнесеннный к единице гладкой
поверхности, то коэффициент теплопередачи для
ребристой стенки равен
1
р.г
1 1 F1
1 2 F2
,
• Тепловой поток отнесённый к единице ребристой
поверхности, то коэффициент теплопередачи для
ребристой стенки равен
1
р.р
,
1 F2 F2 1
1 F1 F1 2

29.

• Для круглой трубы с наружным оребрением:
Q р.к t1 t2 ,
• откуда
1
р.к
,
1
1 d2
F1
ln
1d1 2 d1 2 d 2 F2
где d1 – внутренний диаметр трубы; d2 – наружный диаметр
трубы.
р.к
Вт
1
.
м К

30.

Приведенные формулы
небольшой высоты.
справедливы
для
ребер
• Отношение оребренной поверхности F2 к гладкой F1
называется коэффициентом оребрения.
Точное значение коэффициента теплопередачи для
ребристых поверхностей может быть определено
только экспериментальным путем.

31.

• Пример.
• Определить количество теплоты, передаваемое через 1 м2
ребристой стенки, коэффициент оребрения которой F2/F1=12.
Стенка выполнена из чугуна с теплопроводностью λ=63
Вт/(м·К) и толщиной δ=12 мм.
Коэффициент теплоотдачи от рабочего тела к стенке α1=250
Вт/(м2·К) и α2=12 Вт/(м2·К).
Температура рабочего тела t1=117°С, а температура воздуха
t2=17°С.

32.

• Решение.
• Коэффициент теплопередачи определяем по формуле:
р.г
1
1 1 F1
1 2 F2
,
Считаем, что тепловой поток отнесен к гладкой поверхности.
1
Вт
р.г
90 2
.
0,012 1 1
1
м К
63
12 12
250
• Плотность теплового потока определяем по уравнению:
Вт
q р.г t1 t2 90 117 17 9000 2 .
м

33.

• При гладкой поверхности стенки κ определяем по уравнению:
1
1
Вт
11,4 2
.
0,012 1
1 1 1
м К
63
12
1 2 250
• Плотность теплового потока для гладкой стенки
Вт
q t1 t2 11,4 117 17 1140 2 .
м
Оребрение стенки увеличило теплопередачу в 7,9 раза.
В действительности с учетом изменения коэффициента
теплоотдачи и температуры вдоль ребра эффект от оребрения
может быть значительно меньше.

34. 3. Интенсификации процессов теплопередачи

Практика эксплуатации тепловых аппаратов требует наилучших
условий передачи теплоты от горячего теплоносителя к
холодному.
При решении практических задач теплопередачи в одних
случаях требуется интенсифицировать процесс, в других,
наоборот, всячески тормозить.

35.

• Возможности осуществления требований к интенсификации
процессов теплопередачи вытекают из закономерностей
протекания основных способов передачи теплоты.
Термическое сопротивление стенки можно уменьшить путем
уменьшения толщины стенки и увеличения коэффициента
теплопроводности материала.
R .
Теплоотдача
соприкосновением
может
быть
интенсифицирована путем перемешивания жидкости и
увеличения скорости движения.
При тепловом излучении – путем повышения степени
черноты и температуры излучающей поверхности.

36.

• Вопрос о путях интенсификации процесса теплопередачи
более сложный.
• Правильное его решение может быть получено лишь на основе
тщательного анализа частных условий теплопередачи.
Пример:
Рассмотрим формулу коэффициента теплопередачи для плоской
стенки:
1
1 1
1 2

37.

R 0
• Если термическим сопротивлением стенки пренебречь, то
формула коэффициента теплопередачи примет вид:
1 2
,
1
1 1 2
1 2
1
отсюда следует, что коэффициент теплопередачи всегда меньше
самого малого из коэффициентов теплоотдачи.
• Выявив частные термические сопротивления, можно найти и
решение задачи об интенсификации теплопередачи.

38.

• Пример 1.
В паровом котле коэффициент теплоотдачи от топочных
газов к стенке равен α1=30 Вт/(м2·К), а от стенки к
кипящей воде α2=5000 Вт/(м2·К), теплопроводность
стальной стенки λ=50 Вт/(м·К), толщина стенки δ=0,02
м. Стенку считаем плоской.
При этих условиях коэффициент теплопередачи
κ=29,5 Вт/(м2·К), т.е. он меньше наименьшего α.

39.

• Пример 1.
• Если для увеличения коэффициента теплопередачи κ
улучшить условия теплоотдачи от стенки к воде или
применять более тонкую стенку из теплопроводного
материала, то этими способами увеличить κ не
удается.
• Существенно повысить κ можно лишь тогда, когда
улучшим передачу теплоты от топочных газов к
стенке.

40.

• Пример 2.
• Рассмотрим аппараты, в которых коэффициенты α1 и α2
велики.
В водяном конденсаторе со стороны воды α1=5000 Вт/(м2·К), а со
стороны пара α2=10000 Вт/(м2·К).
Если стенку такого конденсатора изготовить из стали
толщиной 20 мм, то κ=1428 Вт/(м2·К),
если взять стенку толщиной 3 мм, то κ=2770 Вт/(м2·К),
а если сталь заменить красной медью и взять стенку толщиной
1 мм, то κ=3400 Вт/(м2·К).

41.

• Пример 2.
• Данный пример показывает, что при больших
значениях
коэффициентов
теплоотдачи
коэффициент теплопередачи в значительной
степени зависит от теплопроводности стенки.
При изучении условий передачи теплоты в
тепловых
аппаратах
для
интенсификации
теплопередачи
необходимо
стремиться
уменьшить наибольшее сопротивление.