Similar presentations:
Математическая статистика
1.
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА(МС)Математическая статистика изучает и разрабатывает методы сбора, обработки и интерпретации
статистической информации для получения научных и практических выводов.
Теоретической основой математической
статистики являются законы распределения и
предельные теоремы закона больших чисел.
ВЫБОРОЧНЫЙ МЕТОД
Определение 1. Вся совокупность единиц,
2.
подвергаемых обследованию на какой-либопризнак Х, называется генеральной совокупностью (Г.С.).
Количество единиц генеральной совокупности
называется объемом Г.С. и обозначается N.
Различают сплошное и несплошное обследования единиц Г.С. на некоторый признак Х.
К сплошному наблюдению (обследованию)
относятся, например, перепись населения,
медосмотр студентов 1-го курса, ЕГЭ по
русскому языку всех без исключения выпускников школ и т.д.
3.
Виды несплошного наблюдения:1) анкетное;
2) обследование основного массива;
3) монографическое (на какой-либо отдельный
признак);
4) выборочное.
Определение 2. Единицы, отобранные из Г.С.
для обследования на некоторый признак, образуют
выборочную совокупность (в.с.) или выборку.
Количество единиц в.с. называется объемом в.с.
и обозначается n.
4. Преимущество выборочного метода в том, что:
Выборочное обследование применяется в техслучаях, когда:
1) Г.С. очень велика;
2) время, выделенное для обследования, ограничено;
3) обследование связано с уничтожением обследуемых объектов;
4) необходимо проверить точность сплошного
наблюдения.
Преимущество выборочного метода в том, что:
1) он позволяет экономить силы, средства и
время, т.е. является более дешевым и быстрым;
5.
2) позволяет оперативно вмешиваться в ходпроцесса и вносить коррективы на промежуточных этапах;
3) является более точным и объективным.
Различают 2 способа отбора единиц в в.с.:
1) повторный;
2) бесповторный.
При повторном отборе отобранная единица
регистрируется и после обследования на признак Х
возвращается в Г.С. и может участвовать в обследовании на другие признаки.
6.
При бесповторном отборе отобранная единицарегистрируется и после обследования на признак
Х не возвращается в Г.С.
Виды отбора:
не требующие разбиения Г.С. на группы:
1. Собственно-случайный отбор;
2. Механический отбор;
требующие разбиения Г.С. на группы:
3. Типический отбор;
4. Серийный отбор.
От того, правильно ли организован отбор единиц
в в.с., зависят точность и качество результатов и
выводов выборочного обследования.
7.
При собственно-случайном отборе каждаяединица Г.С. имеет равные шансы попасть в
выборку: единицы Г.С. регистрируются, снабжаются номером и участвуют в жеребьевке.
При механическом отборе единицы Г.С.
упорядочиваются, и в соответствии с процентом
отбора извлекается определенное количество
единиц, например, при 25%-й выборке отбирается каждая четвертая единица.
Типический отбор применяется в тех случаях,
когда Г.С. неоднородна по составу. Тогда по
некоторому признаку Г.С. разбивается на однородные типические группы и из каждой группы
8.
собственно-случайным или механическимспособами извлекаются единицы в в.с.
Серийный отбор применяется в тех случаях,
когда Г.С. однородна по составу. Тогда вся Г.С.
разбивается на группы или серии и среди этих
серий собственно-случайным или механическим
способами извлекаются единицы в в.с.
Выборка должна быть репрезентативной
(представительной),т.е. должна правильно
отражать исследуемый признак Г.С.
Выборочный метод решает следующие задачи:
9.
1) Организация выборочной совокупности;2) Вычисление числовых характеристик
( параметров) в.с.;
3) Оценка параметров Г.С. и выводы о них;
4) Определение необходимой численности
выборки.
Статистическое распределение выборки
Пусть из Г.С. объемом N отобрана выборка
объема n, которая обследуется на некоторый
признак Х (например, з/плата рабочих, % жирнос
ти молока, диаметр деталей и т. д.).
10.
Определение . Значения признака Х: х1, х2,…,[ВТ1]
…, хn называются вариантами, а упорядоченная
последовательность вариант называется
вариационным рядом.
Вариационный ряд можно задавать как в виде
последовательности значений хi, так и поинтервально.
Определение . Число повторений варианты хi
называется ее частотой и обозначается mi, причем
[ВТ1]
n
mi = n.
i 1
Последовательность частот mi называется
частотным рядом.
11.
Определение . Соответствие между вариационным и частотным рядами назыв. статистическимраспределением выборки.
Способы задания статистического распределения выборки: табличный и графический.
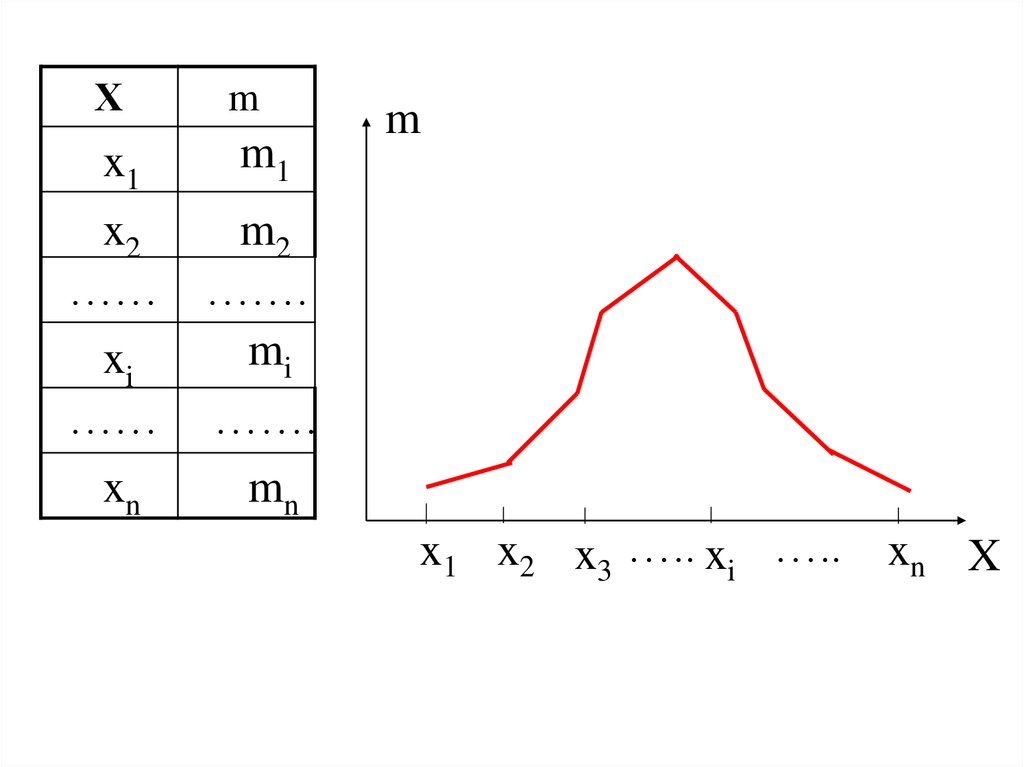
a) вариационный ряд задается в виде
последовательности вариант:
[ВТ1]
12.
Хm
m1
x1
x2
m2
…… …….
mi
xi
…… …….
xn
mn
m
x1 x2 x3 ….. xi ….. xn X
13.
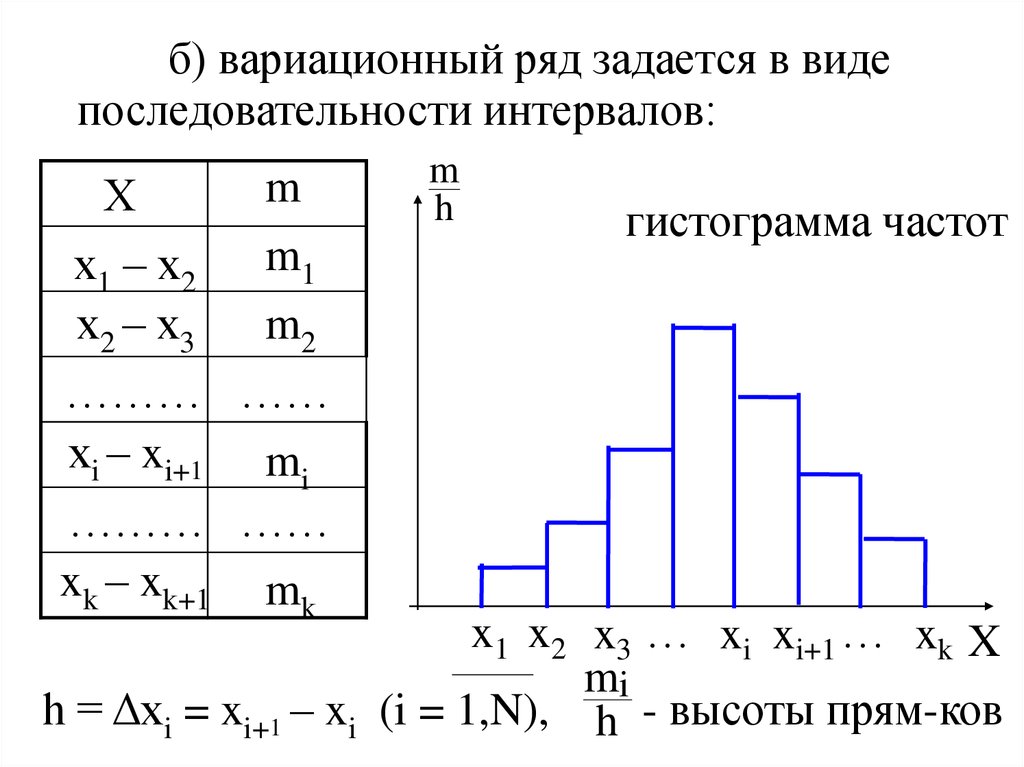
б) вариационный ряд задается в видепоследовательности интервалов:
m
Х
m1
х1 – х2
х 2 – х3
m2
……… ……
хi – xi+1 mi
……… ……
xk – xk+1 mk
m
h
гистограмма частот
x1 x2 x3 … xi xi+1 … xk X
mi
h = Δxi = xi+1 – xi (i = 1,N), h - высоты прям-ков
14.
Числовые характеристики в.с.Определение. Числовые характеристики (или
статистики) – это параметры, которые в сжатой
форме отражают особенности Г.С.
К ним относятся:
1) выборочная средняя – среднее взвешенное
значение признака в в.с.:
k
~
1 ximi ,
x= n
i 1
где
k
n = mi
i 1
15.
2) выборочная дисперсия – среднее взвешенноеквадратов отклонений значений признака от
среднего значения:
k
1
σ2(Х) = n (xi x)2mi
i 1
выборочная дисперсия – мера колеблемости
значений признака около среднего значения.
3) выборочная доля – доля единиц в в.с., обладающих тем или иным признаком:
w m
n
16.
где m – число единиц в в.с., обладающих исследуемым признаком, n – объем выборки. Тогда(n – m) – число единиц в.с., не обладающих этим
признаком, отсюда:
n m
1–w=1- m
n = n
Числовые характеристики Г.С.
1) Генеральная средняя – среднее взвешенное
значение признака в Г.С.:
L
x = 1 xiMi ,
N i 1
где
L
N = Mi
i 1
17.
2) Генеральная дисперсия – дисперсия признакав Г.С.:
L
D(X) 2 (X) 1 (xi x)2 Mi
N i 1
0
3) Генеральная доля – доля единиц, обладающих
тем или иным признаком в Г.С.:
p M
N
,
где М – число единиц, обладающих этим
признаком в Г.С.
18.
MТогда q = 1 – p = 1 - N
- доля единиц, не обладающих этим признаком в
Г.С.
Характеристики в.с. отличаются от соответствующих характеристик Г.С.
Определение. Отклонение характеристик
в.с. от соответствующих характеристик Г.С.
называется ошибкой репрезентативности или
ошибкой выборки.
Определение. Средняя ошибка репрезентативности μ показывает, на сколько в среднем
параметры в.с. отклонятся от соответствующих
параметров Г.С.
19.
Определение. Предельная ошибка репрезентативности Δ показывает наибольшее отклонение характеристики в.с. от соответствующейхарактеристики Г.С.
Предельная и средняя ошибки выборки
связаны между собой соотношением:
Δ = tμ,
где t называется коэффициентом надежности
или коэффициентом достоверности.
20.
Оценки параметров распределенияКакую-либо характеристику Г.С. ( х, σ02 или w)
обозначим через θ, а соответствующую характе~
ристику в.с. – через θ.
Определение 1. Оценка генеральной характеристики, заданная одним числом, называется
точечной.
Определение 2. Оценка генеральной характеристики, заданная двумя числами, называется
интервальной.
Определение 3. Интервал
~
~
θ - Δθ ≤ θ ≤ θ + Δθ
21.
или~
│θ – θ│≤ Δθ
называется доверитель-
ным интервалом для θ, а Δθ называется
точностью оценки.
Определение 4. Вероятность того, что θ
попадет в доверительный интервал, называется
надежностью γ оценки θ, т.е.:
~
P(│θ – θ│≤ Δθ) = γ
22.
Требования к числовым характеристикамПусть из Г.С. объема N извлекаются всевозможные повторные выборки объемов n и
~
~
~
вычисляются θi – значения θ, затем находят M(θ)
~
Определение. Оценка θ называется
несмещенной, если при любом объеме выборки:
~
M(θ) = θ.
~
Если же M(θ) ≠ θ, то оценка называется
смещенной.
23.
Определение. Состоятельной называется~
статистическая оценка θ, которая при n ∞
сходится по вероятности к оцениваемому
параметру θ:
~
lim P(│θ – θ │≤ Δ ) = 1
n
∞
Если имеются несколько несмещенных
~
оценок θ, вычисленных при одинаковых n, то
лучшая из них – та, которая имеет минимальный
разброс.
24.
Определение. Эффективной называется~
несмещенная состоятельная оценка θ, которая при
~
заданном n имеет минимальную дисперсию D(θ).
Теорема 1. Математическое ожидание
среднего арифметического одинаково распределенных СВ равна математическому ожиданию
каждой из этих СВ, а дисперсия среднего арифметического n CВ в n раз меньше дисперсии
каждой из них:
X1 X2... X n
M(
) M(Xi)
n
25.
X1 X2... X n 1D(
) D(Xi)
n
n
X1 X2... X n
1
(
) (Xi)
n
n
~
Теорема 2. Выборочная средняя х является
несмещенной и состоятельной оценкой
генеральной средней х .
Теорема 3. Выборочная доля w является
несмещенной и состоятельной оценкой генеральной доли p .
26.
Теорема 4. Исправленная выборочная дисперсия:n 2
2
S (X) = n 1 σ (X)
является несмещенной и состоятельной оценкой
генеральной дисперсии D(X) = σ02(X).
Теорема Чебышева-Ляпунова
( для средней)
С вероятностью, равной Ф(t) = γ , где t –
коэффициент надежности, можно утверждать, что
отклонение генеральной средней от выборочной
27.
средней по абсолютной величине не превзойдетпредельной ошибки выборки Δх:
~
P(│ x – x │≤ Δх ) = Ф(t) = γ,
где предельная ошибка выборки для средней
при собственно-случайном отборе:
2x - для повторного отбора;
Δхповт= t n
2x (1 n ) - для бесповторного отбора
Δхбесповт= t n
N
28.
Значение γ = Ф(t) отыскивается в таблицеПриложения 2.
Теорема Чебышева-Ляпунова
( для доли)
С вероятностью, равной Ф(t) = γ можно
утверждать, что абсолютная величина отклонения генеральной доли от выборочной доли не
превзойдет предельной ошибки выборки Δw:
P(│ p – w │≤ Δw ) = Ф(t) = γ,
29.
где предельная ошибка выборки для долипри собственно-случайном отборе:
w(1 w)
Δwповт = t
n
- для повторного отбора;
w(1 w) (1 n )
n
Δwбесп = t
N
-для бесповторного
отбора
Из теорем Чебышева-Ляпунова следует, что
с вероятностью γ = Ф(t) доверительный интервал для генеральной средней:
30.
~x - Δх ≤ x ≤ x~ + Δх
,
a доверительный интервал для генеральной
доли:
w - Δw ≤ p ≤ w + Δw
Из формулы:
2x
Δх= t n
следует, что, чем больше объем в.с. n, тем меньше
предельная ошибка Δх, а значит, и средняя ошибка
31.
2μх = x
n
С другой стороны, чем выше надежность Ф(t), тем
больше коэффициент надежности t и тем больше
ошибка Δх. При бесповторном отборе:
Δхбесповт < Δхповт,
а значит, доверительный интервал точнее, чем при
повторном отборе.Такие же выводы справедливы
для ошибок Δw по доле.
Приведенные выше формулы предельных
ошибок для средней и для доли имеют место при
собственно- случайном отборе. Все формулы,
32.
приведенные для собственно- случайного отбора,справедливы и для механического способа отбора.
Сводка формул для собственно- случайного
и механического способов отбора
N – объем Г.С., n – объем в.с.
Характеристики в.с.
~ 1 k
х = n ximi - выборочная средняя, где k – число
i 1
вариант вариационного ряда
k
n = mi
i 1
33.
k~x)2mi - выборочная дисперсия
1
2
(
x
i
σx = n
i 1
m
w = n - выборочная доля
Ошибки репрезентативности(выборки)
2
n)
2
x
(
1
Для средней: Δхповт= t nx , Δхбесп= t n
N
2
n
2
x
μхповт = nx , μхбесп = n (1 )
N
2
2w
n
Для доли:
Δwповт= t nw , Δ
=
t
wбесп
n (1 N )
34.
2μwповт = nw ,
2w
n
μwбесп =
n (1 N )
Доверительные интервалы
~
~
Для средней:
x - Δх ≤ x ≤ x + Δх
Для доли:
w - Δw ≤ p ≤ w + Δw
Сводка формул для типического
способа отбора
N – объем Г.С., n – объем в.с.;
l – количество типических групп;
kj – число вариант в j–й типической группе(j = 1, l)
35.
Nj - объем j–й типической группы в Г.С.;nj - объем j–й типической группы в в.с.;
kj
nj = mi ,
i 1
1
n = n j
j 1
Внутригрупповые характеристики
j–й типической группы
kj
~ 1
xj = n ximi - внутригрупповая средняя j–й
j
i 1
типической группы;
kj
~ 2
2
1
σj = n (xi x j) m j - внутригрупповая дисперсия;
j
j 1
36.
mjwj = n j - внутригрупповая доля
Общие(межгрупповые) характеристики в.с.
~ 1 l ~x n - общая(межгрупповая) средняя;
x =n j j
j 1
l
σх2 = n1 j2n j - общая дисперсия по средней;
j 1
l
w = n1 w jn j - общая доля;
j 1
l
1
σw2 = n w j(1 w j)n j - общая дисперсия по доле;
j 1
37.
Предельные ошибки выборки2x (1 n )
2x , Δ
Для средней: Δхповт= t n
n
хбесповт= t
N
Для доли: Δwповт = t
2w (1 n )
,
Δ
=
t
n
wбесп
n
N
2w
Доверительные интервалы записываются так же,
как и при собственно-случайном отборе.
Сводка формул для серийного
способа отбора
S – общее число серий в Г.С.
s – число серий, отобранных в в.с.
38.
j – номер серии, j = 1, s.~
xj – средняя в j –й серии;
wj – доля в j –й серии;
Общие характеристики в.с.
s ~ ~
~ 1 s ~x j
1
2=
2
(
x
x
)
σ
j
х=s
;
х
s
j 1
j 1
s
w = s1 w j ;
j 1
σw
s
2
1 (w j w)2
= s
j 1





































 mathematics
mathematics








