Similar presentations:
Площадь криволинейной трапеции и интеграл
1.
Площадькриволинейной
трапеции и интеграл.
у
х
2.
Найти первообразную функции:3.
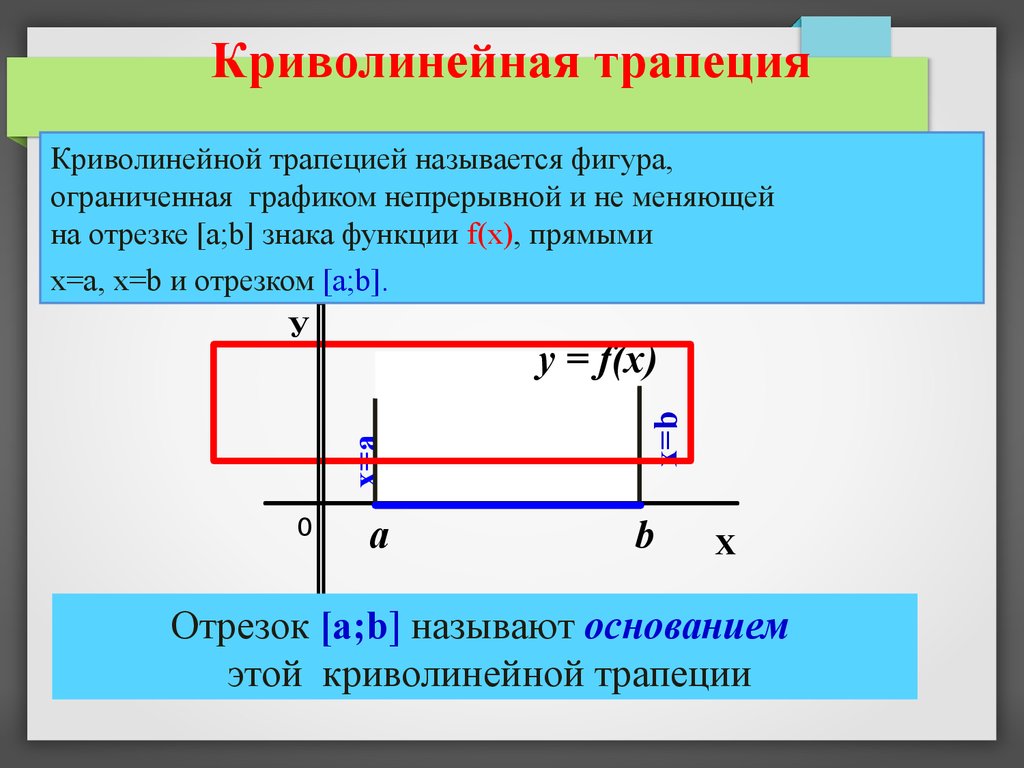
Криволинейная трапецияКриволинейной трапецией называется фигура,
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b] знака функции f(х), прямыми
х=а, x=b и отрезком [а;b].
У
0
a
x=b
х=а
y = f(x)
b
Х
Отрезок [a;b] называют основанием
этой криволинейной трапеции
4.
Площадь криволинейной трапеции.где F(x) – любая первообразная функции f(x).
5.
Формула Ньютона-Лейбница1643—1727
1646—1716
6.
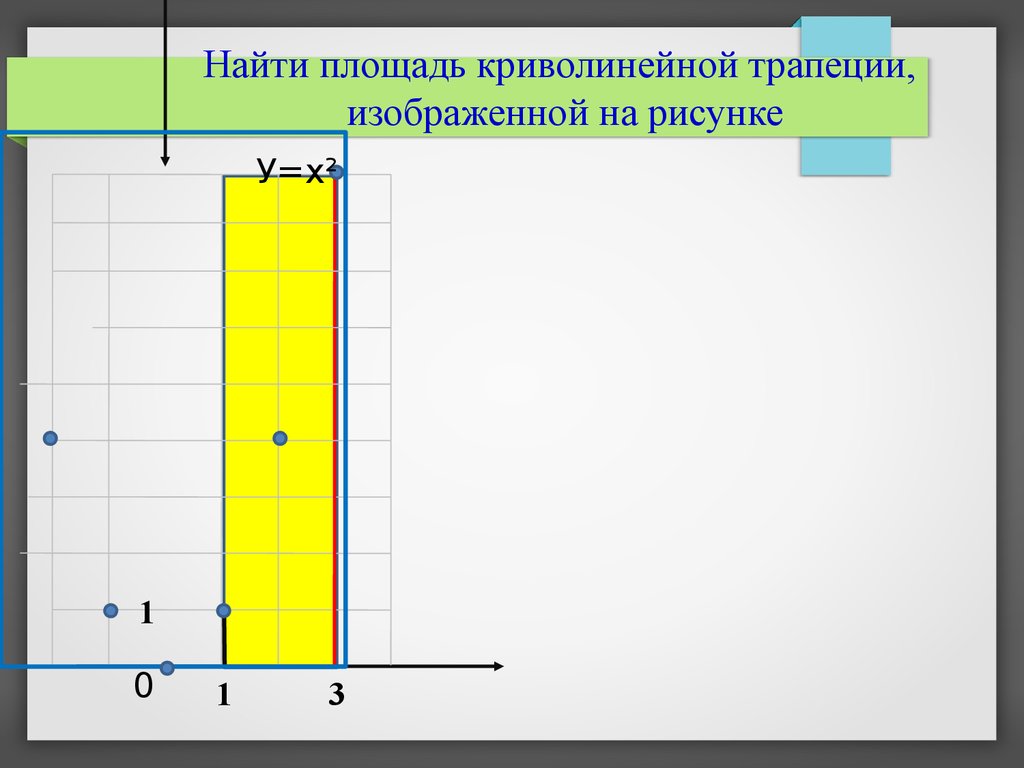
Найти площадь криволинейной трапеции,изображенной на рисунке
У=х²
1
0
1
3
7.
Найти площадь криволинейной трапеции,изображенной на рисунке
y=sinx
I
1
0
I
-1
8.
9.
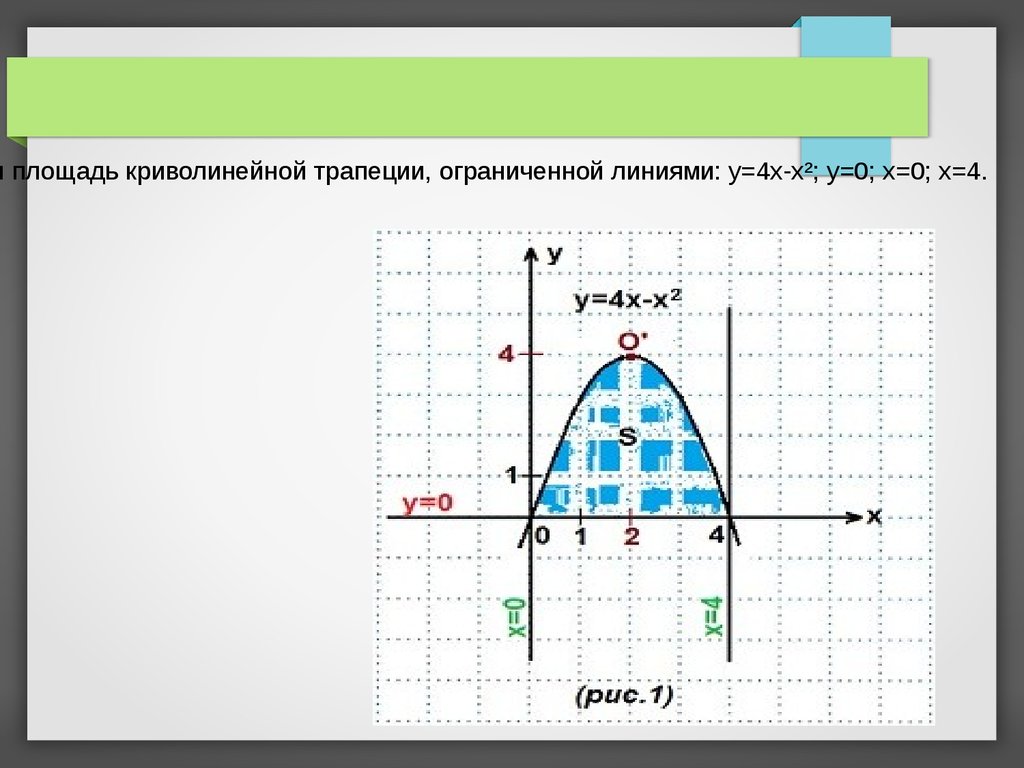
и площадь криволинейной трапеции, ограниченной линиями: y=4x-x²; y=0; x=0; x=4.10.
Решение. Строим графики данных линий.1) y=4x-x² — парабола (вида y=ax²+bx+c). Запишем данное уравнение
в общем виде: y=-x²+4x. Ветви этой параболы направлены вниз,
так как первый коэффициент а=-1<0.
Вершина параболы находится
в точке O′(m; n), где
О′(2; 4). Нули функции (точки пересечения графика с осью Ох) найдем из уравнения:
4х-х²=0.
Выносим х за скобки, получаем: х(4-х)=0. Отсюда, х=0 или х=4.
Абсциссы точек найдены, ордината равна нулю — искомые точки: (0; 0) и (4; 0).
2) y=0 — это ось Ох;
3) х=0 — это ось Оy;
4) х=4 — прямая, параллельная оси Оy и отстоящая от нее на 4 единичных
отрезка вправо.
Площадь построенной криволинейной трапеции находим по (ф. Н-Л).
У нас f (x)=4x-x², a=0, b=4.
11.
Найти площадь криволинейной трапеции, ограниченной линиями:12.
Решение:13.
Вычислить площадь фигуры, ограниченной линиями:у = 4х – х², у = 5, х = 3
Хₒ = 2, Уₒ = 4
14.
Sф = S(ОАВД) – S(ОСД)Sпрям. =
S(ОСД) = F(3) – F(0),
где F(x) первообразная для функции
f(х) = 4х – х²
F(х)=
Sф = 15 – 9 = 6.
; SОСД=








 mathematics
mathematics








