Similar presentations:
Площадь криволинейной трапеции и интеграл
1. Площадь криволинейной трапеции и интеграл.
ух
2.
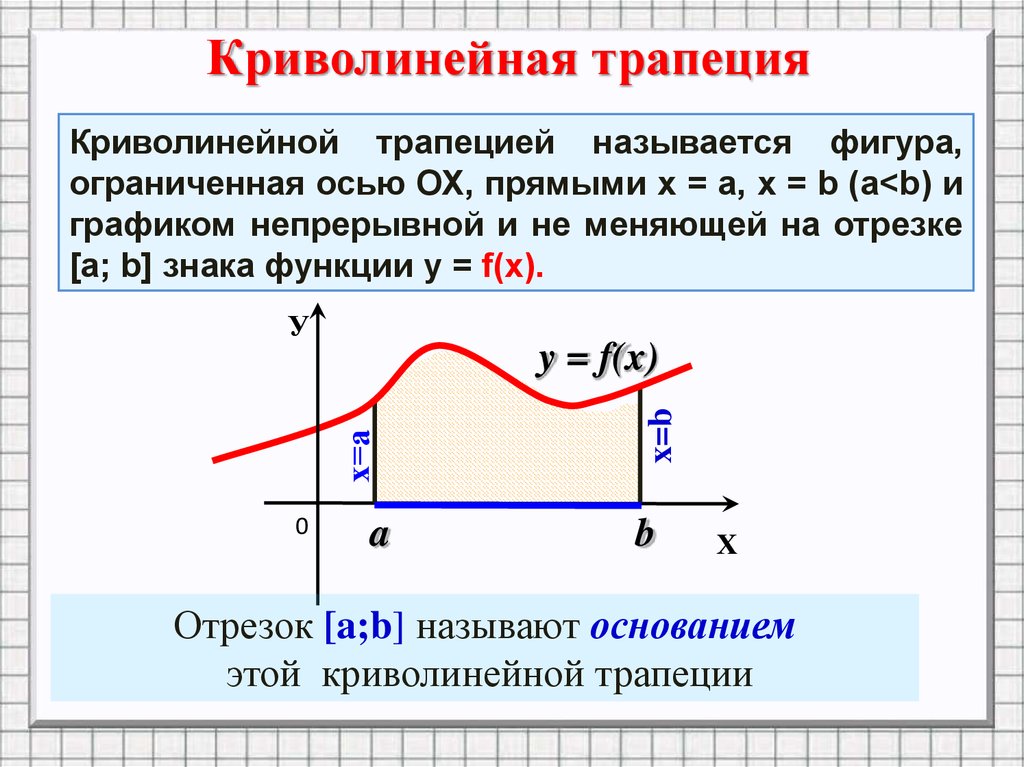
Криволинейная трапецияКриволинейной трапецией называется фигура,
ограниченная осью ОХ, прямыми х = а, x = b (a<b) и
графиком непрерывной и не меняющей на отрезке
[а; b] знака функции у = f(х).
У
0
a
x=b
х=а
y = f(x)
b
Х
Отрезок [a;b] называют основанием
этой криволинейной трапеции
3.
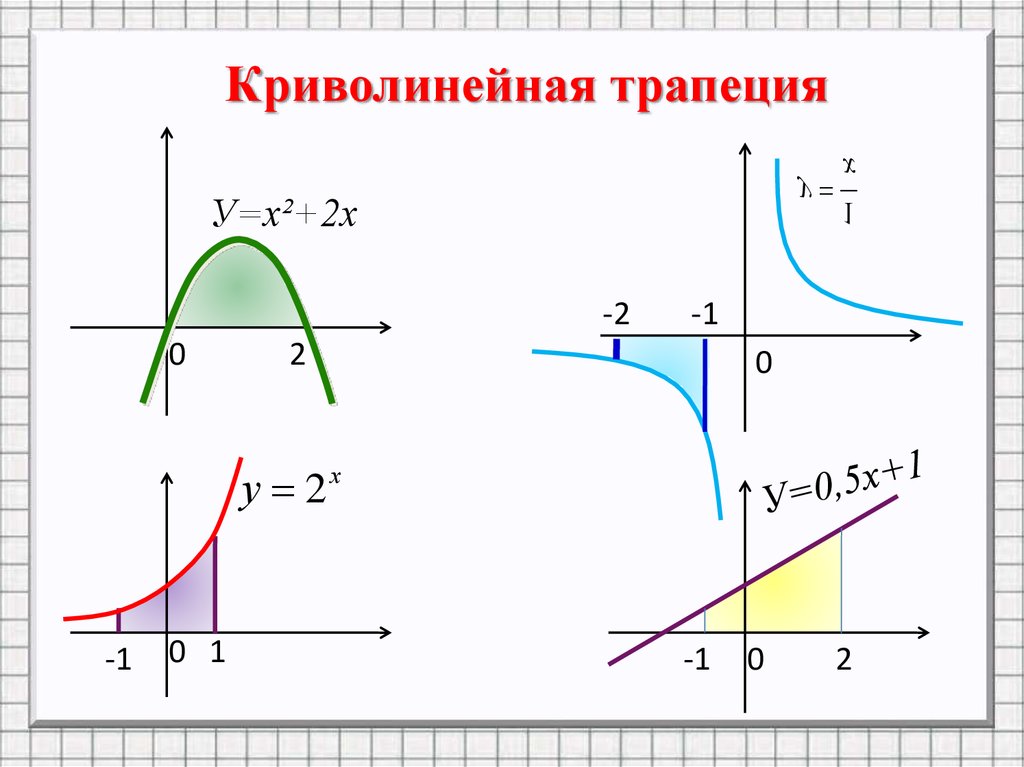
Криволинейная трапециях
у
1
У=х²+2х
-2
0
2
у 2
-1
0 1
-1
0
х
-1
0
2
4.
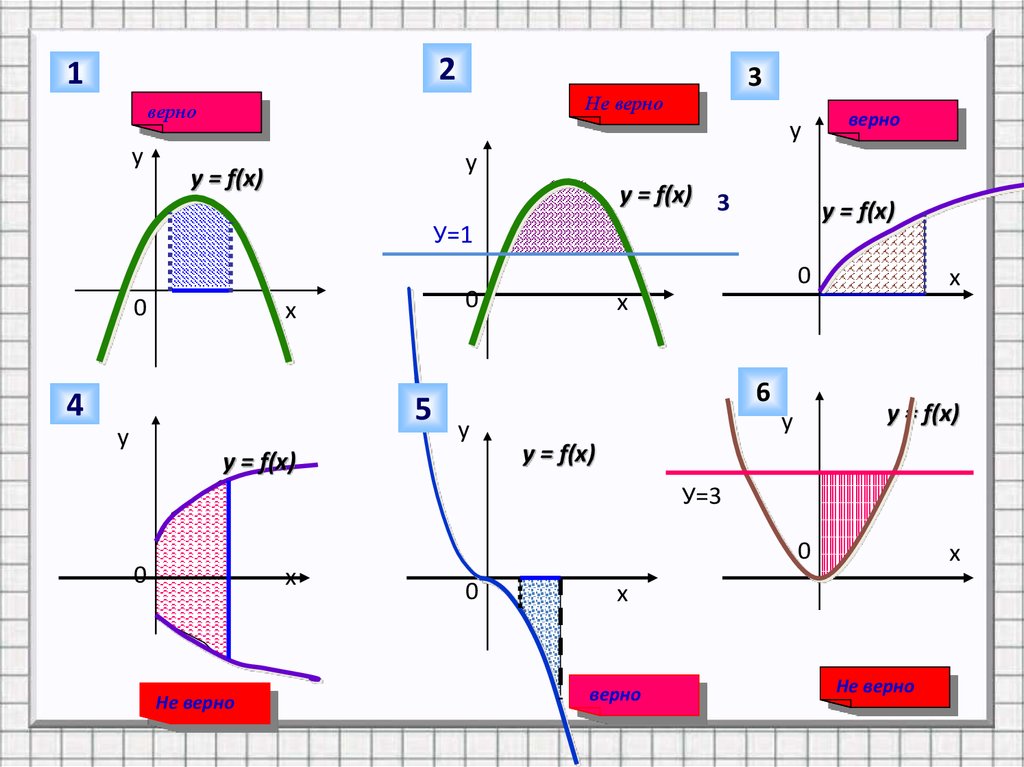
Какие из заштрихованных на рисункефигур являются криволинейными
трапециями, а какие нет?
Заполнить таблицу
№1
№2
№3
№4
№5
№6
Да/нет
5.
21
Не верно
верно
у
3
у
у
y = f(x)
y = f(x) 3
y = f(x)
У=1
0
0
0
х
4
5
у
верно
х
6
у
y = f(x)
х
y = f(x)
у
y = f(x)
У=3
0
0
х
Не верно
0
х
х
верно
Не верно
6. Изобразить криволинейную трапецию, ограниченную графиком функции y = (x-1)2, осью Ox и прямой x = 2.
y x 12
1
0
1
01
x=2
y
12
x
7.
Задача (о перемещении точки).По
прямой
движется
точка.
Зависимость
скорости
от
времени
выражается формулой v=v(t); пусть для
определённости
v(t)>0.
Найти
перемещение точки за промежуток
времени [a;b].
8.
Если бы движение было равномерным, то задача решалась бы оченьпросто: s = vt, т.е. s = v(b-a). Для неравномерного движения приходится
использовать те же идеи, на которых было основано решение предыдущей
задачи.
1) Разобьём отрезок [а; b] на n равных частей.
2) Рассмотрим отдельно k-ый участок [tk; tk+1] и будем
считать, что скорость на этом промежутке времени
постоянна, а именно такая, как, например, в момент
времени tk . Итак, считаем, что v = v(tk).
3) Найдём приближённое значение перемещения
точки sk за промежуток времени [tk ; tk+1]:
sk ≈ v(tk)·Δ tk,
4) Найдём приближённое значение перемещения s:
s ≈ Sn, где Sn= s 0 + s 1 + s 2 + … + s k + … + s n-1 =
v(t0)Δt0 + v(t1)Δt1 + v(t2)Δt2 + … + v(tk)Δtk + … + v(tn-1)Δtn-1.
5) Точное значение перемещения вычисляется по
формуле:
9.
Формула Ньютона-ЛейбницаS F (b) F (a)
b
1643—1727
f ( x)dx F (b) F (a)
a
b
S f ( x)dx
a
1646—1716
10.
Теорема. Если функция y = f(x) непрерывна наотрезке [а; b], то справедлива формула
b
f ( x)dx F (b) F (a ),
a
где F(x) – первообразная для f(x).
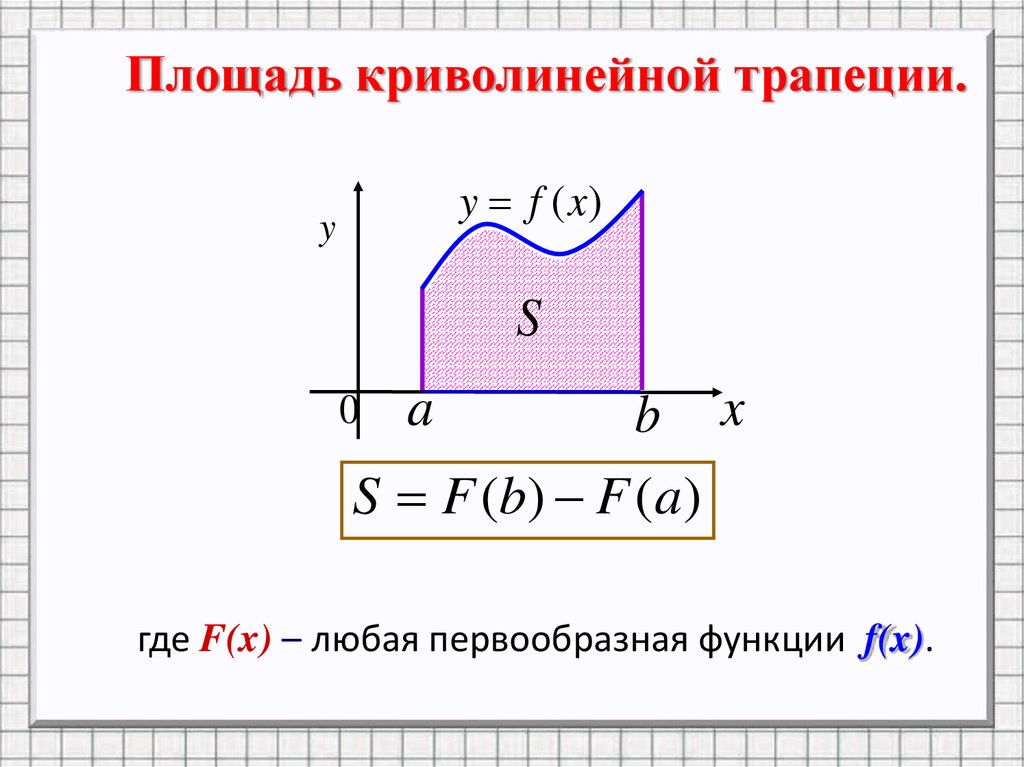
11.
Площадь криволинейной трапеции.y f (x)
y
S
0
a
b
x
S F (b) F (a)
где F(x) – любая первообразная функции f(x).
12.
Найти площадь криволинейной трапеции,изображенной на рисунке
У=х²
y
b
S
f ( x ) dx
a
3
S
х 2 dx F (3) F (1)
1
33 13
2
8 ( кв.ед)
3
3
3
1
0
1
3
x
13.
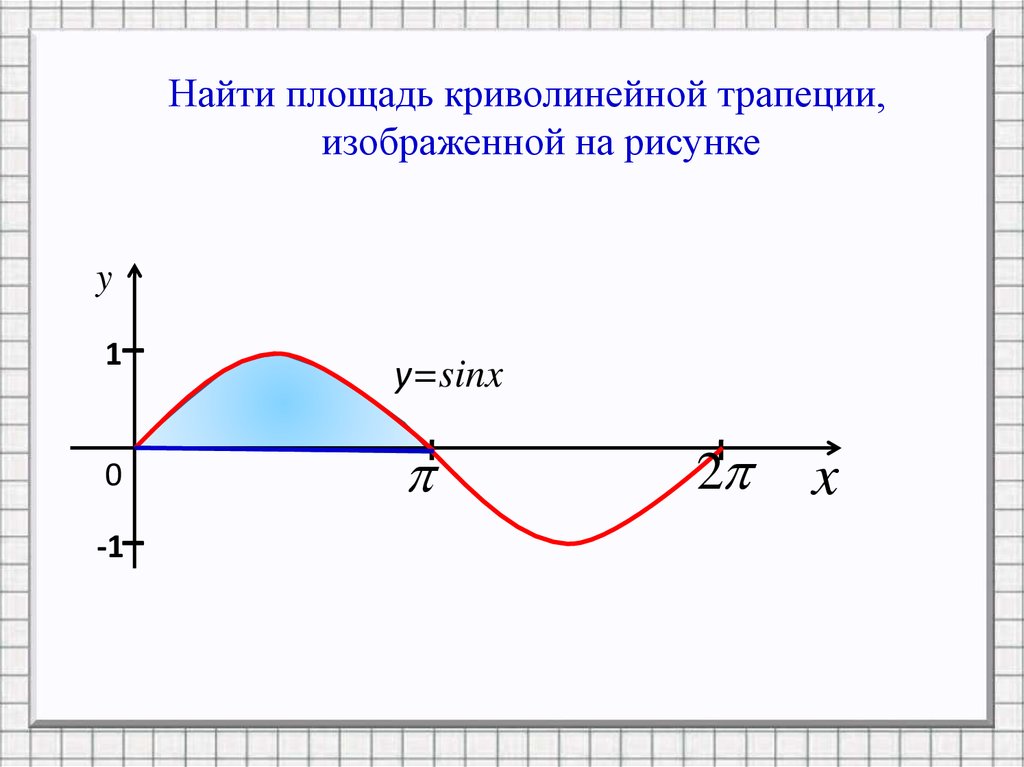
Найти площадь криволинейной трапеции,изображенной на рисунке
y
I
1
0
I
-1
y=sinx
2
x
14.
источникиУчебник
Алгебра и начала математического анализа 10-11 Ш.А.Алимов и др
http://go.mail.ru/search_images?q=%
http://go.mail.ru/search_images?q=%








 mathematics
mathematics








