Similar presentations:
Осевая и центральная симметрии
1.
ОСЕВАЯИ ЦЕНТРАЛЬНАЯ
СИММЕТРИИ
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU
2. Две точки А и А1 называются СИММЕТРИЧНЫМИ ОТНОСИТЕЛЬНО ПРЯМОЙ а, если эта прямая проходит через середину отрезка АА1 и
перпендикулярна к немуА
a
А1
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU
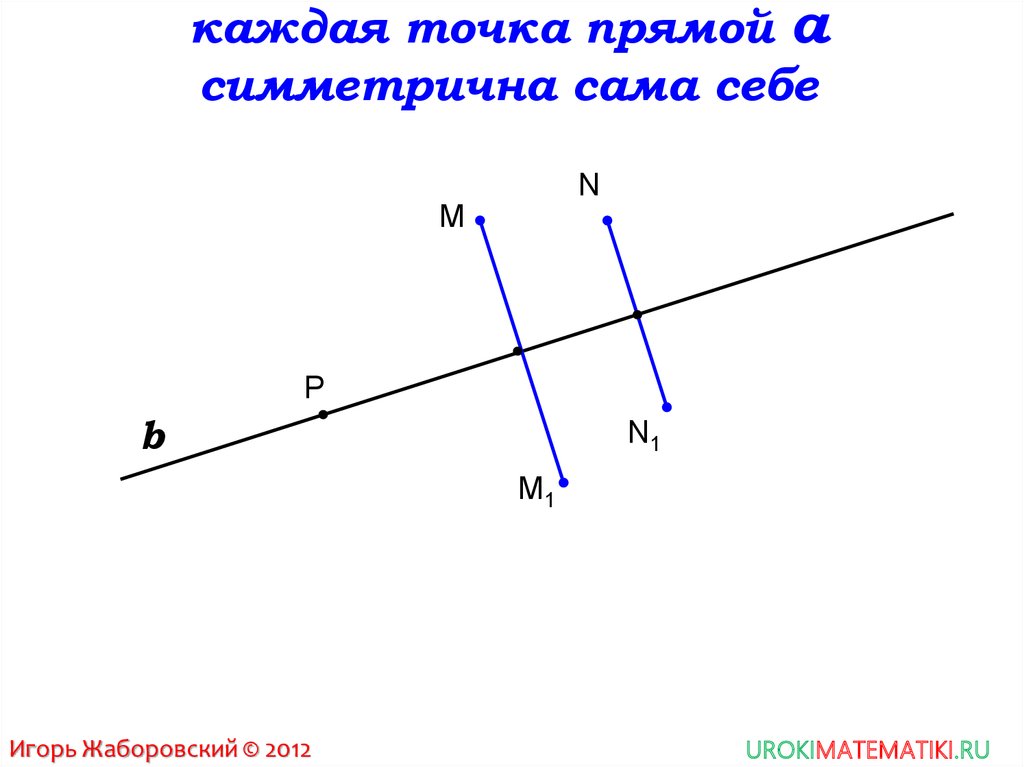
3. каждая точка прямой а симметрична сама себе
NМ
P
b
N1
М1
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU
4. Фигура называется СИММЕТРИЧНОЙ ОТНОСИТЕЛЬНО ПРЯМОЙ а, если для каждой точки фигуры симметричная ей точка относительно прямой а
также принадлежит этой фигурепрямая
а – ось симметрии фигуры
фигура обладает осевой симметрией
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU
5.
Игорь Жаборовский © 2012UROKIMATEMATIKI.RU
6.
Игорь Жаборовский © 2012UROKIMATEMATIKI.RU
7. Две точки А и А1 называются СИММЕТРИЧНЫМИ ОТНОСИТЕЛЬНО ТОЧКИ О, если О – середина отрезка АА1
А1точка О симметрична сама себе
P
M
N
Игорь Жаборовский © 2012
M1
Q
UROKIMATEMATIKI.RU
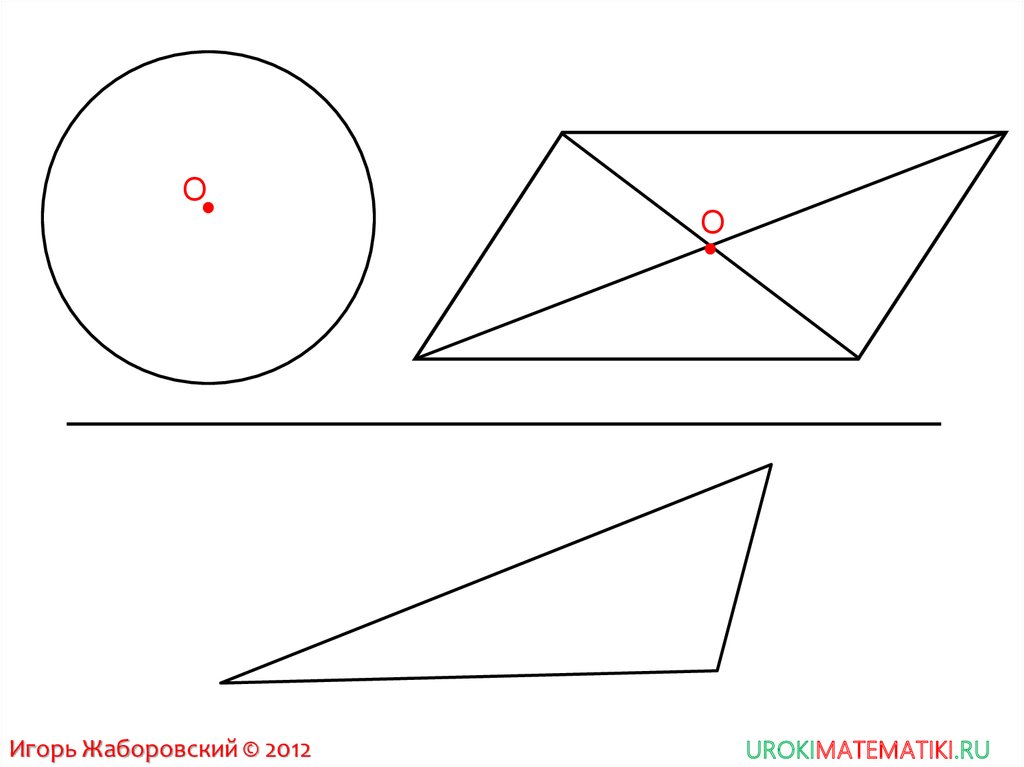
8. Фигура называется СИММЕТРИЧНОЙ ОТНОСИТЕЛЬНО ТОЧКИ О, если для каждой точки фигуры симметричная ей точка относительно точки О
также принадлежит этой фигуреточка О – центр симметрии фигуры
фигура обладает центральной
симметрией
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU
9.
ОИгорь Жаборовский © 2012
О
UROKIMATEMATIKI.RU
10.
Игорь Жаборовский © 2012UROKIMATEMATIKI.RU
11.
Игорь Жаборовский © 2012UROKIMATEMATIKI.RU









 mathematics
mathematics








