Правильные многогранники и их построение

1. Правильные многогранники и их построение.

Работу выполнила:
ученица 11 класса
МОУ «Карсинская СОШ»
Моторина Анастасия
900igr.net
1

2. Цели и задачи:

Дать понятие правильных многогранников ( на основе
определения многогранников).
Доказать почему существует только 5 типов
правильных многогранников.
Рассмотреть свойства правильных многогранников.
Познакомить с историческими фактами, связанными с
теорией правильных многогранников.
Показать, как можно с помощью куба построить
другие виды правильных многогранников.
2

3. Существует пять типов правильных многогранников

октаэдр
тетраэдр
гексаэдр
икосаэдр
додекаэдр
3

4. Определение многогранника:

Многогранник – это часть пространства,
ограниченная совокупностью конечного числа
плоских многоугольников, соединённых таким
образом, что каждая сторона любого
многогранника является стороной ровно одного
многоугольника. Многоугольники называются
гранями, их стороны – рёбрами, а вершины –
вершинами.
4

5. Правильным называется многогранник, у которого все грани являются правильными многоугольниками, и все многогранные углы при вершинах рав

Правильным называется
многогранник, у которого
все грани являются
правильными
многоугольниками, и все
многогранные углы при
вершинах равны.
Приведён пример правильного многогранника
(икосаэдр), его гранями являются правильные
(равносторонние) треугольники.
5

6. В каждой вершине многогранника должно сходиться столько правильных n – угольников, чтобы сумма их углов была меньше 3600. Т.е должна выполнят

В каждой вершине многогранника должно сходиться
столько правильных n – угольников, чтобы сумма их углов
0
была меньше 360 . Т.е должна выполняться формула
0
βk < 360 ( β-градусная мера угла многоугольника,
являющегося гранью многогранника, k – число
многоугольников,
сходящихся
в
одной
вершине
многогранника.)
название
β
k
Сумма плоских углов
тетраэдр
60
3
180
октаэдр
60
4
240
икосаэдр
60
5
300
гексаэдр
90
3
270
додекаэдр
108
3
324
6

7.

ТЕТРАЭДР
Правильный многогранник, у которого грани правильные
треугольники и в каждой вершине сходится по три ребра и по
три грани. У тетраэдра: 4 грани, четыре вершины и 6 ребер.
назад
7

8. ОКТАЭДР

Правильный многогранник, у которого грани- правильные
треугольники и в каждой вершине сходится по четыре ребра и
по четыре грани. У октаэдра: 8 граней, 6 вершин и 12 ребер
назад
8

9. ИКОСОЭДР

Правильный многогранник, у
которого грани - правильные
треугольники и в вершине
сходится по пять рёбер и
граней. У икосаэдра:20
граней, 12 вершин и 30 ребер
назад
9

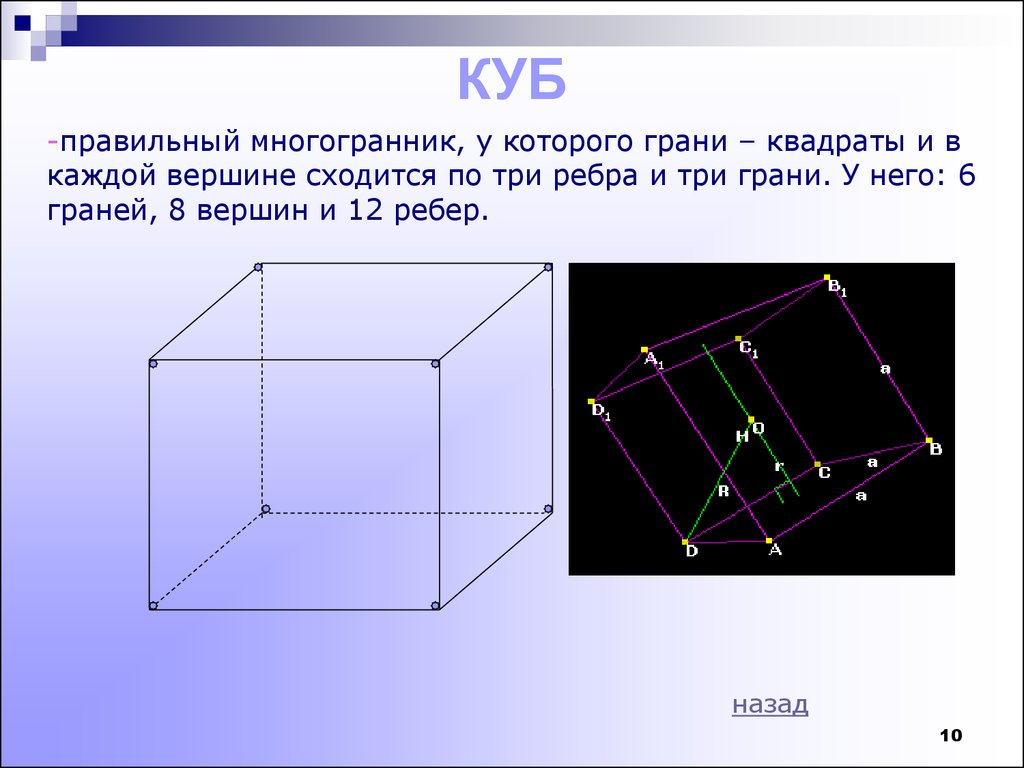
10. КУБ

-правильный многогранник, у которого грани – квадраты и в
каждой вершине сходится по три ребра и три грани. У него: 6
граней, 8 вершин и 12 ребер.
назад
10

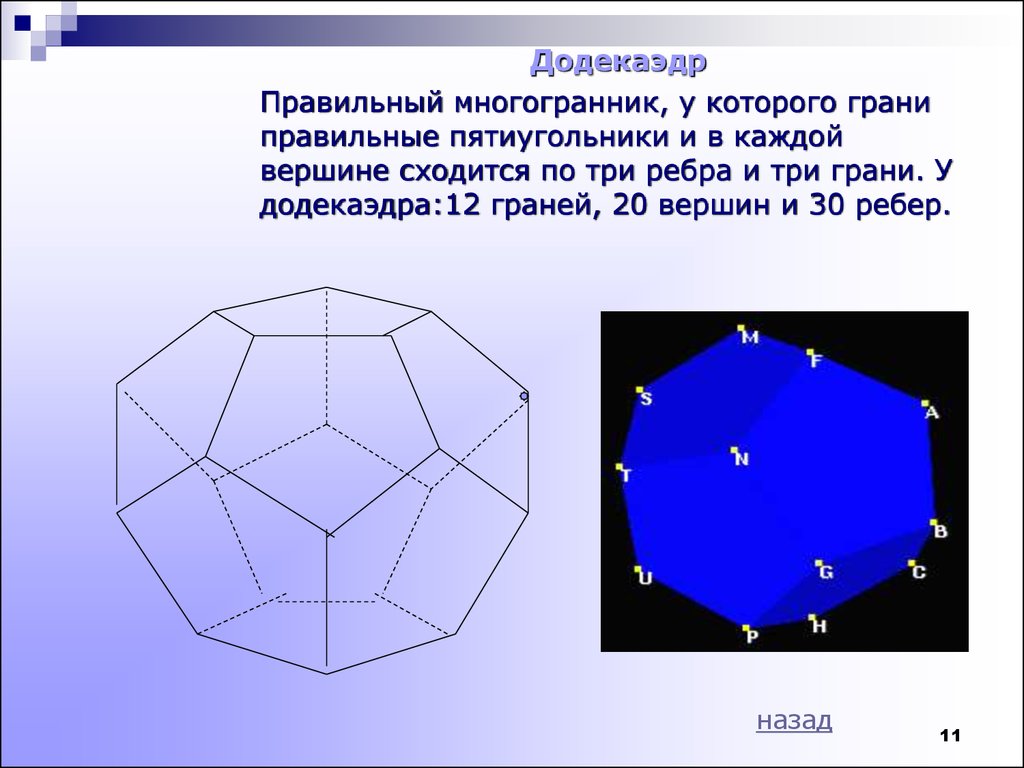
11.

Додекаэдр
Правильный многогранник, у которого грани
правильные пятиугольники и в каждой
вершине сходится по три ребра и три грани. У
додекаэдра:12 граней, 20 вершин и 30 ребер.
назад
11

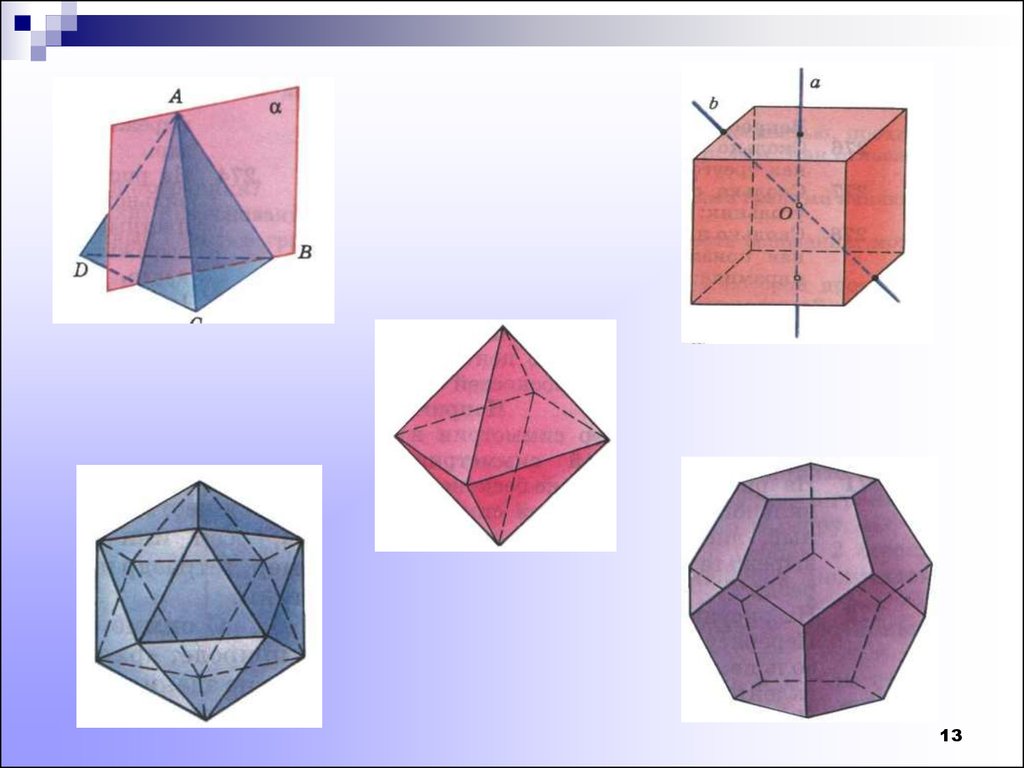
12. Элементы симметрии правильных многогранников

тетраэдр
октаэдр
икосаэдр
гексаэдр
додекаэдр
Центры
симметрии
-
1
1
1
1
Оси
симметрии
3
9
15
9
15
Плоскости
симметрии
6
9
15
9
15
12

13.

13

14. Немного истории

Все типы правильных многогранников были известны в Древней Греции –
именно им посвящена завершающая, XIII книга «Начал» Евклида.
14

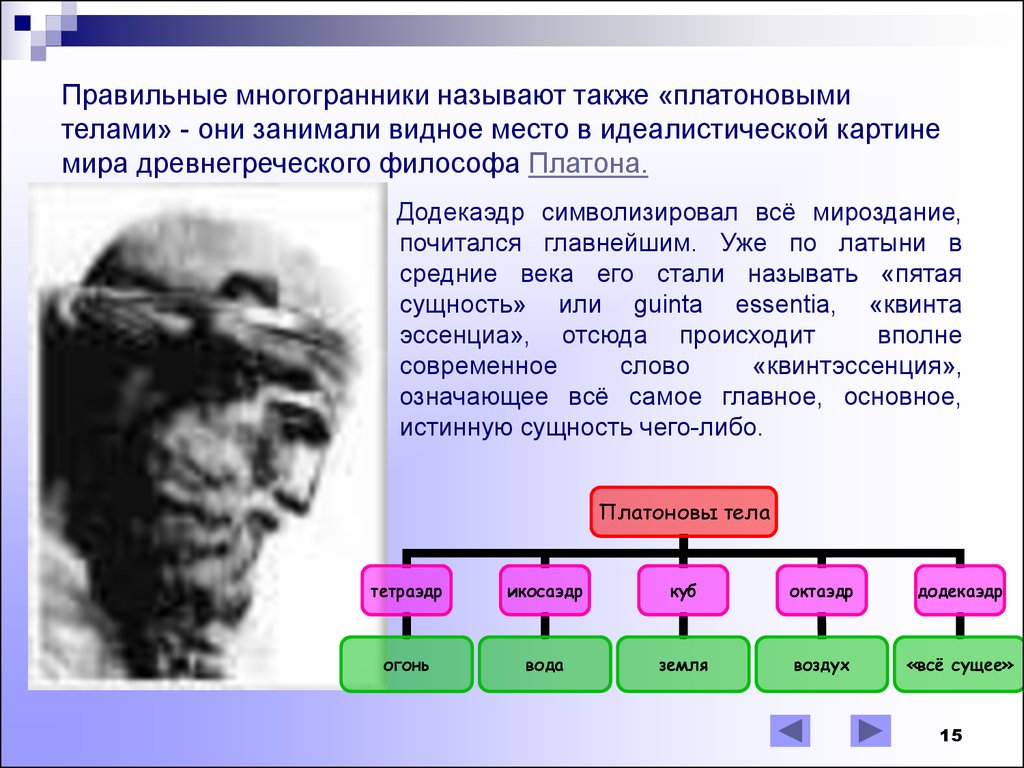
15. Правильные многогранники называют также «платоновыми телами» - они занимали видное место в идеалистической картине мира древнегреческог

Правильные многогранники называют также «платоновыми
телами» - они занимали видное место в идеалистической картине
мира древнегреческого философа Платона.
Додекаэдр символизировал всё мироздание,
почитался главнейшим. Уже по латыни в
средние века его стали называть «пятая
сущность» или guinta essentia, «квинта
эссенциа», отсюда происходит
вполне
современное
слово
«квинтэссенция»,
означающее всё самое главное, основное,
истинную сущность чего-либо.
Платоновы тела
тетраэдр
икосаэдр
куб
октаэдр
додекаэдр
огонь
вода
земля
воздух
«всё сущее»
15

16. Олицетворение многогранников.

16

17. Дюрер. Меланхолия

17

18. Тайна мировоззрения.

18

19. Выводы:

Многогранник называется
правильным, если:
Он выпуклый;
Все его грани равные правильные
многоугольники;
В каждой вершине сходится одно
число граней;
Все его двугранные углы равны.
19

20. Евклид

Построение с
помощью куба
23

21. Платон

Закон взаимности
24

22. Определение правильного многоугольника

Звездчатые правильные
многогранники
25

23. Построение с помощью куба

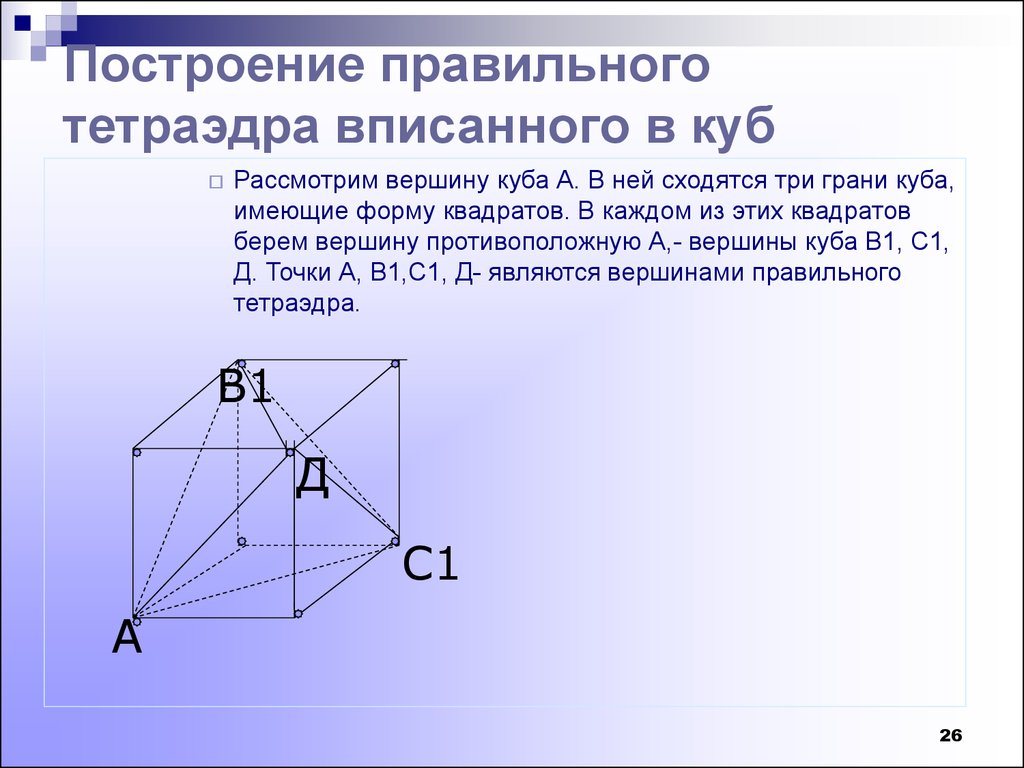
Построение правильного
тетраэдра вписанного в куб
Рассмотрим вершину куба А. В ней сходятся три грани куба,
имеющие форму квадратов. В каждом из этих квадратов
берем вершину противоположную А,- вершины куба В1, С1,
Д. Точки А, В1,С1, Д- являются вершинами правильного
тетраэдра.
В1
Д
С1
А
26

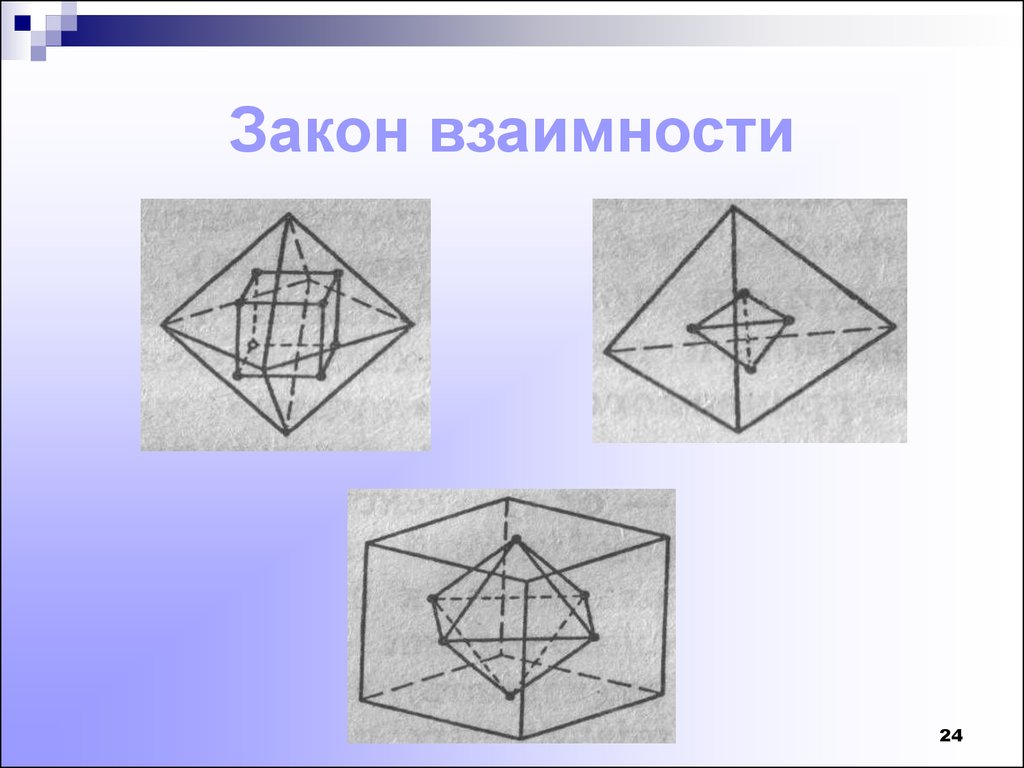
24. Закон взаимности

Построение правильного
тетраэдра
27

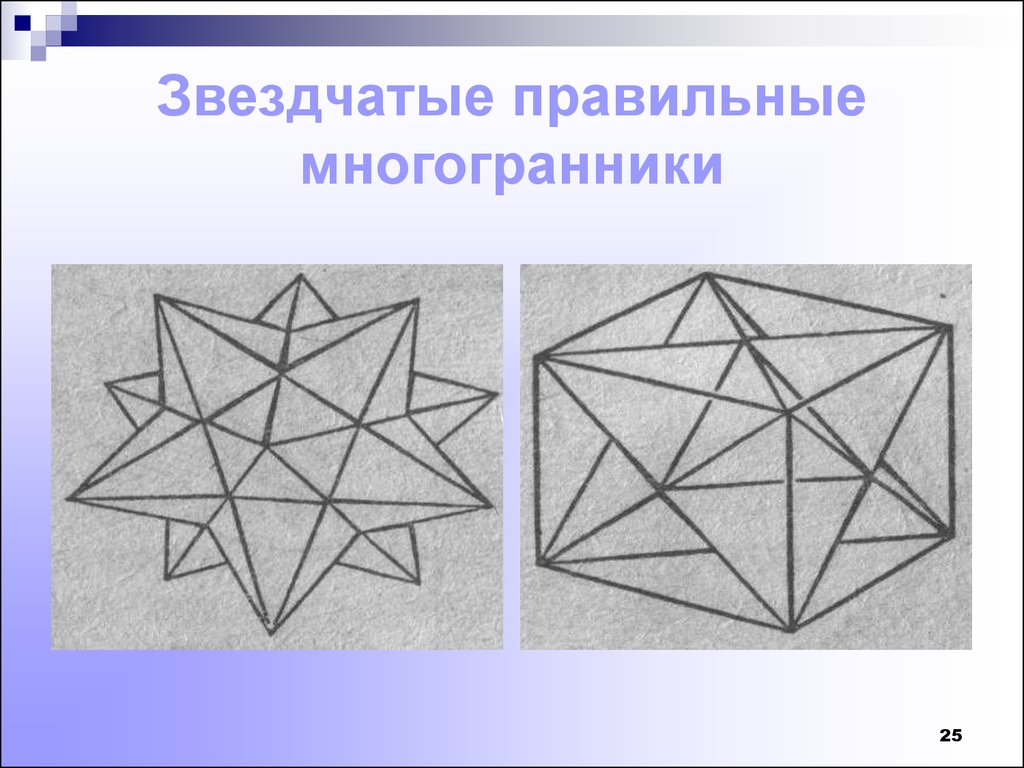
25. Звездчатые правильные многогранники

Построение правильного
октаэдра, вписанного в
данный куб
Выбираем куб. В нем
последовательно
проводим отрезки: слабо
видимыми линиями
соединяем попарно
между собой вершины
каждой грани. Точки
пересечения этих
диагоналей соединяем
между собой.
28

26. Построение правильного тетраэдра вписанного в куб

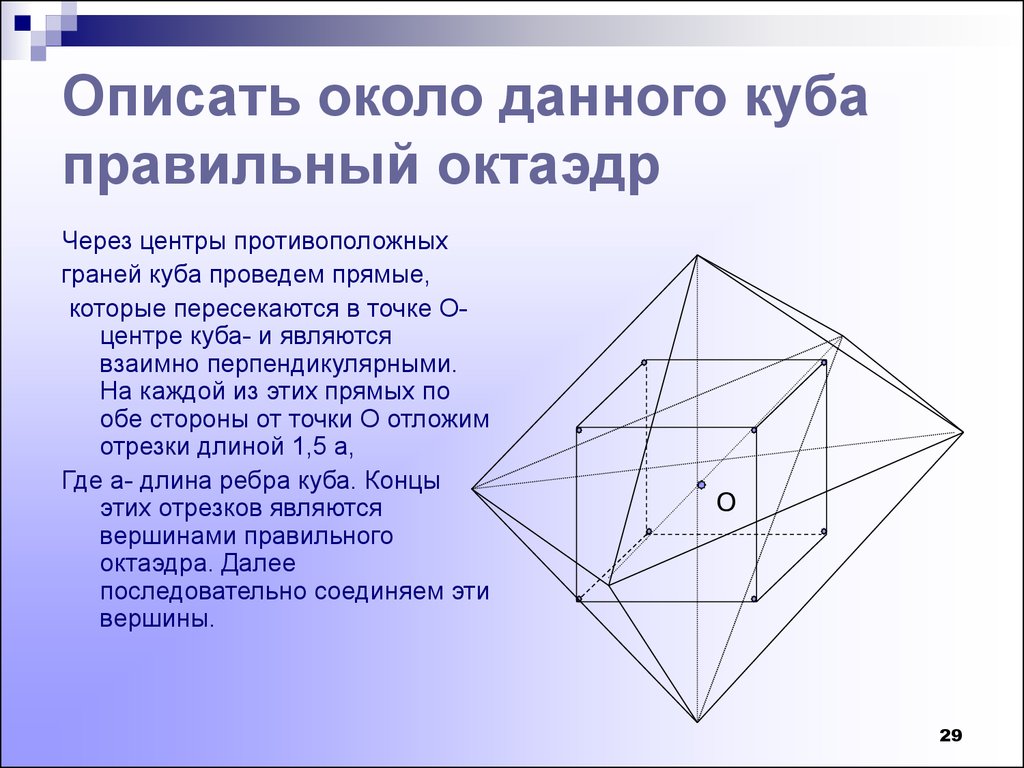
Описать около данного куба
правильный октаэдр
Через центры противоположных
граней куба проведем прямые,
которые пересекаются в точке Оцентре куба- и являются
взаимно перпендикулярными.
На каждой из этих прямых по
обе стороны от точки О отложим
отрезки длиной 1,5 а,
Где а- длина ребра куба. Концы
этих отрезков являются
вершинами правильного
октаэдра. Далее
последовательно соединяем эти
вершины.
O
29

27. Построение правильного тетраэдра

Построение икосаэдра,
вписанного в куб
Поместим на средних
линиях граней куба по
одному отрезку одинаковой
длины с концами на равных
расстояниях от ребер.
Расположим отрезки и
выберем их длину так,
чтобы соединяя концы
отрезка одной грани с
концом отрезка другой
грани получить
равносторонний
треугольник, причем из
каждой вершины должны
выходить пять ребер.
30

28. Построение правильного октаэдра, вписанного в данный куб

Построение додекаэдра,
описанного около куба
На каждой грани куба строим
« четырехскатную крышу»,
две грани которойтреугольники и дветрапеции. Такие треугольник
и трапецию получим, если
построим правильный
пятиугольник, у которого
диагональ равна ребру куба.
Стороны этого пятиугольника
будут равны ребрам
додекаэдра, а построенные с
помощью диагонали
треугольник и трапеция
окажутся фрагментами
«четырехскатной крыши»
31