Similar presentations:
Избранные главы неорганического материаловедения. (Лекция 2)
1.
Избранные главы неорганического материаловеденияЛекция 2
1. Роль фазовых диаграмм в материаловедении
2. Определения: системы, фазы, компоненты
3. Химический потенциал
4. Правило фаз
5. Однокомпонентные системы
6. Двухкомпонентные системы
Классификация превращений в 2-х компонентных системах
Моновариантные процессы
2.
МатериалыРавновесные
Неравновесные
3.
Фазовая диаграмма системы отражает РАВНОВЕСНЫЕсостояния и РАВНОВЕСНЫЕ превращения
Ni
Si
4.
Правило Таммана:Диффузионные взаимодействия в
твердофазных системах
становятся возможными при
Т ~> 0,6 Тпл
5.
Фазовая диаграмма физико-химической системы - ключ кпониманию особенностей материала и его технологии
SiO2 –
Al2O3
муллит
расплав
расплав
3Al2O3•2SiO2
третичный муллит
6.
Физико-химическая система –совокупность выделенных из
окружающей среды материальных
объектов, между которыми
возможен обмен энергией и
веществом.
7.
Гетерогенная система –физико-химическая система,
содержащая поверхности
раздела, на которых
происходит скачкообразное
изменение какого-либо
свойства.
8.
Фаза – гомогенная часть гетерогеннойсистемы
компоненты
3
=
1 =
3 (пар)
+
+
1
1
2
2
2 =
+
1
2
1
1
2
1
1
2
2
9.
Компоненты – индивидуальныевещества, составляющие систему.
Число компонентов – минимальное
число индивидуальных веществ , из
которых может быть составлена
любая фаза системы.
10.
3-х компонентнаясистема Ti-Al-O при
низком рО2
2-х компонентная
система TiO2-Al2O3при
высоком рО2
Число компонентов может изменяться
при изменении внешних условий,
определяющих равновесие в системе.
Al
11.
Определение химического потенциала компонентаСвободная энергия
системы
Число молей j -компонента
o
μj = μj + RTlnaj
aj = γjcj
12.
Химическое равновесиегетерогенной системы
достигается тогда, когда
химические потенциалы каждого
из компонентов равны во всех
фазах системы.
13.
До установления равновесияРавновесное состояние
Фаза 2
Фаза 1
Фаза 2 Фаза 3
Фаза 1
Фаза 3
μ11
μ12 μ13
μ11
μ21
μ22 μμ2233
1
μ
μ221
μ12
μ13
2
3
2
3
μ
μ
μ22 μ2 2
14.
При равновесии k фаз вn- компонентной системе:
1
μ1 =
μ1
2=
μ1 =…
3
μ11
… = μ1
фазы
компоненты
k
15.
μ11= μ12= μ13 =… … = μ1k1
2
3
…
…
k
μ2 = μ2 = μ2 =
= μ2
1
2
3
…
…
k
μ3 = μ3 = μ3 =
= μ3
………………………………
………………………………
μn1= μn2= μn3 =… … = μnk
k-1 равенств
Всего n(k-1) уравнений
n
строк
16.
Система уравнений имеет определенноерешение, если
число уравнений равно числу переменных.
Переменные:
Состав равновесных фаз
Температура
Давление
Другие внешние потенциалы, влияющие на состояние системы (???)
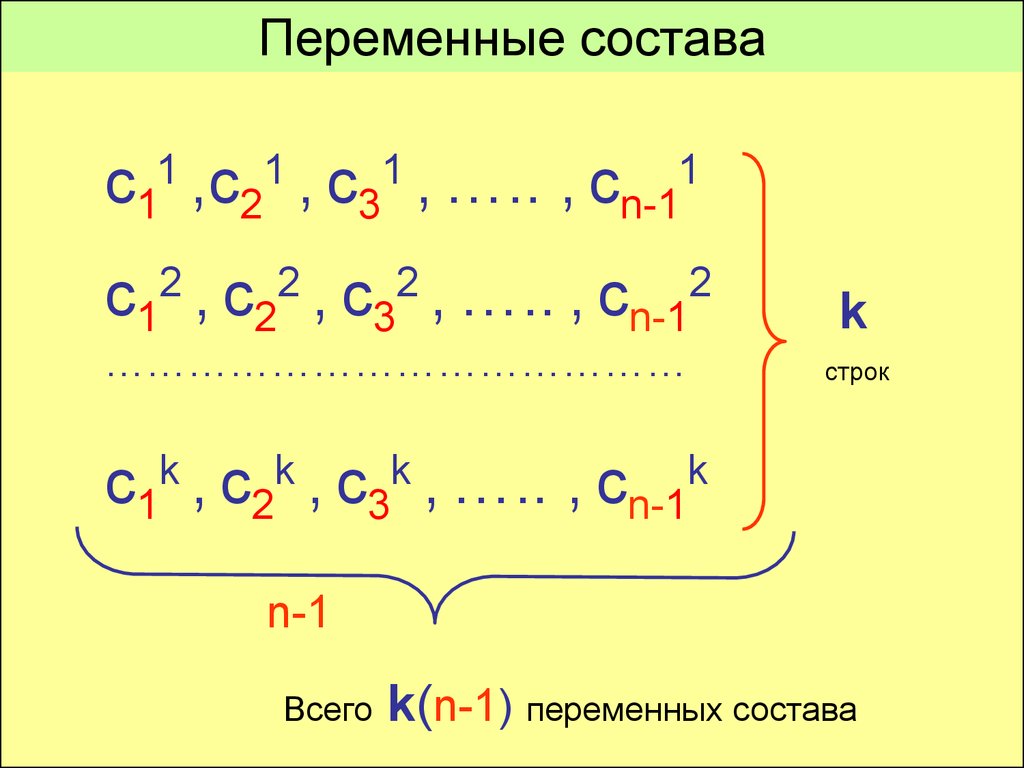
17.
Переменные составас11 ,с21 , с31 , ….. , cn-11
с12 , с22 , с32 , ….. , cn-12
……………………………………
k
строк
с1k , с2k , с3k , ….. , сn-1k
n-1
Всего
k(n-1) переменных состава
18.
Всего переменных:k(n-1) +2
Число уравнений связи:
n(k -1)
Число степеней свободы f,
f = (Число переменных) – (Число уравнений связи)
f = k(n-1) +2 - n(k -1) = n +2 - k
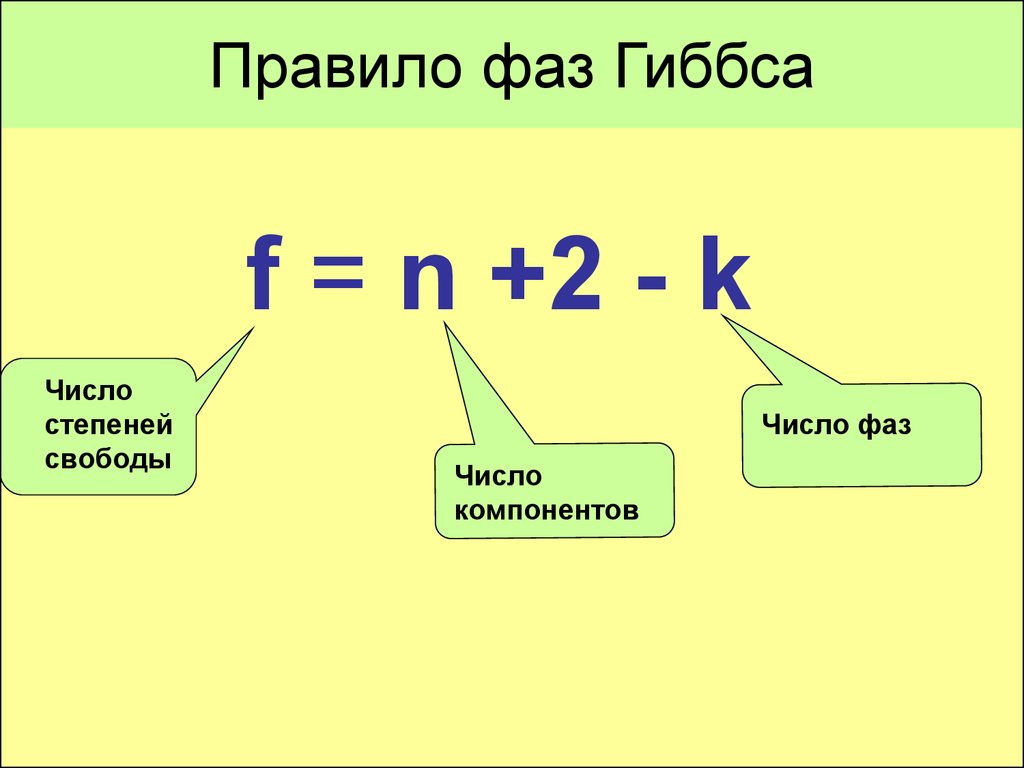
19. Правило фаз Гиббса
f = n +2 - kЧисло
степеней
свободы
Число фаз
Число
компонентов
20.
Принцип соответствияВсякому комплексу фаз на
диаграмме состояния соответствует
свой геометрический образ,
причем мерность этого образа равна
вариантности системы в данном
равновесном комплексе.
Вариантность ≡ число степеней свободы
21.
Фазовые диаграммыоднокомпонентных систем
22.
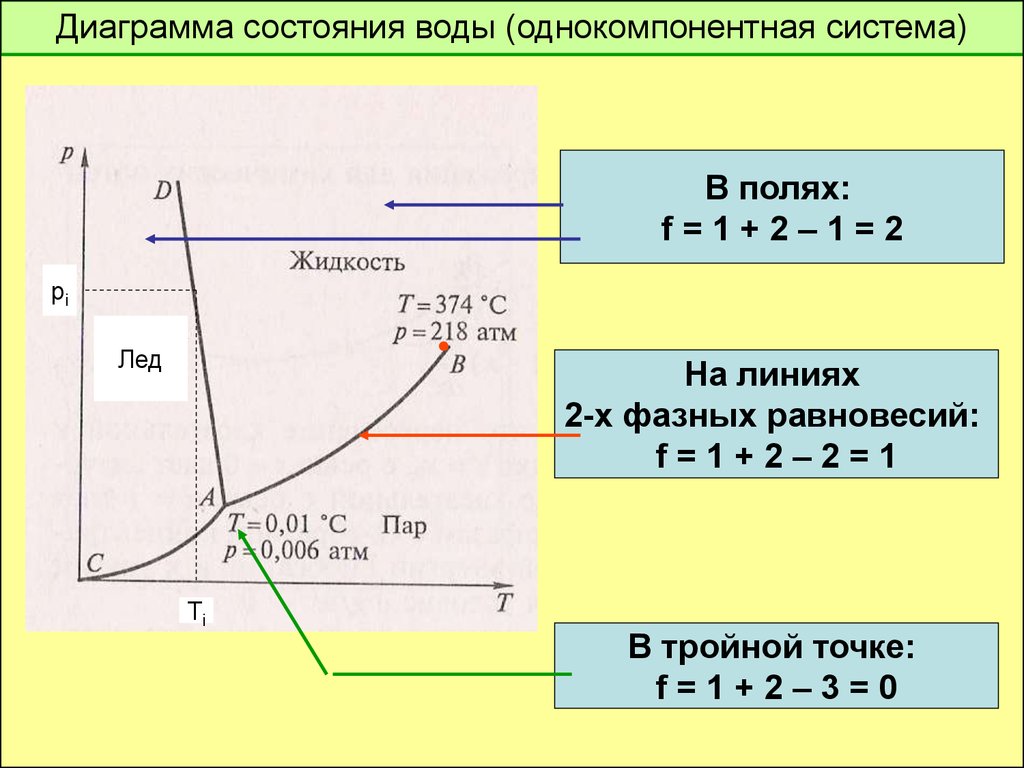
Диаграмма состояния воды (однокомпонентная система)В полях:
f=1+2–1=2
pi
Лед
Ti
На линиях
2-х фазных равновесий:
f=1+2–2=1
В тройной точке:
f=1+2–3=0
23.
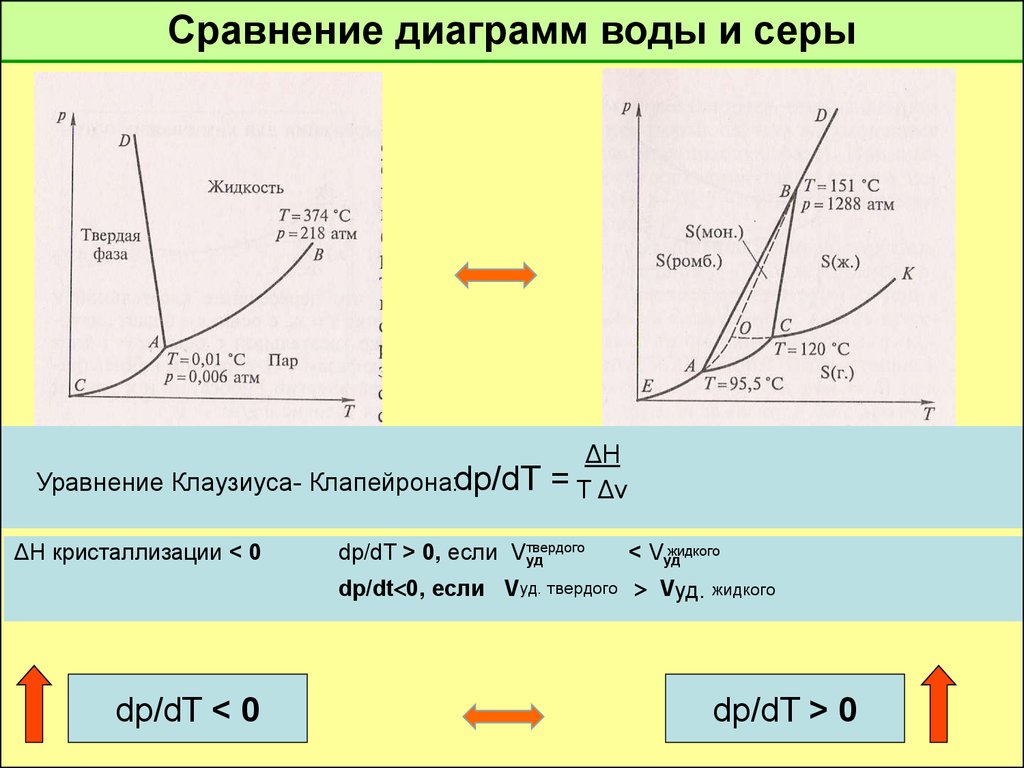
Сравнение диаграмм воды и серыУравнение Клаузиуса- Клапейрона:dp/dT
ΔH кристаллизации < 0
ΔH
= T Δv
твердого
dp/dT > 0, если Vуд
жидкого
< Vуд
dp/dt 0, если Vуд. твердого Vуд. жидкого
dp/dT < 0
dp/dT > 0
24.
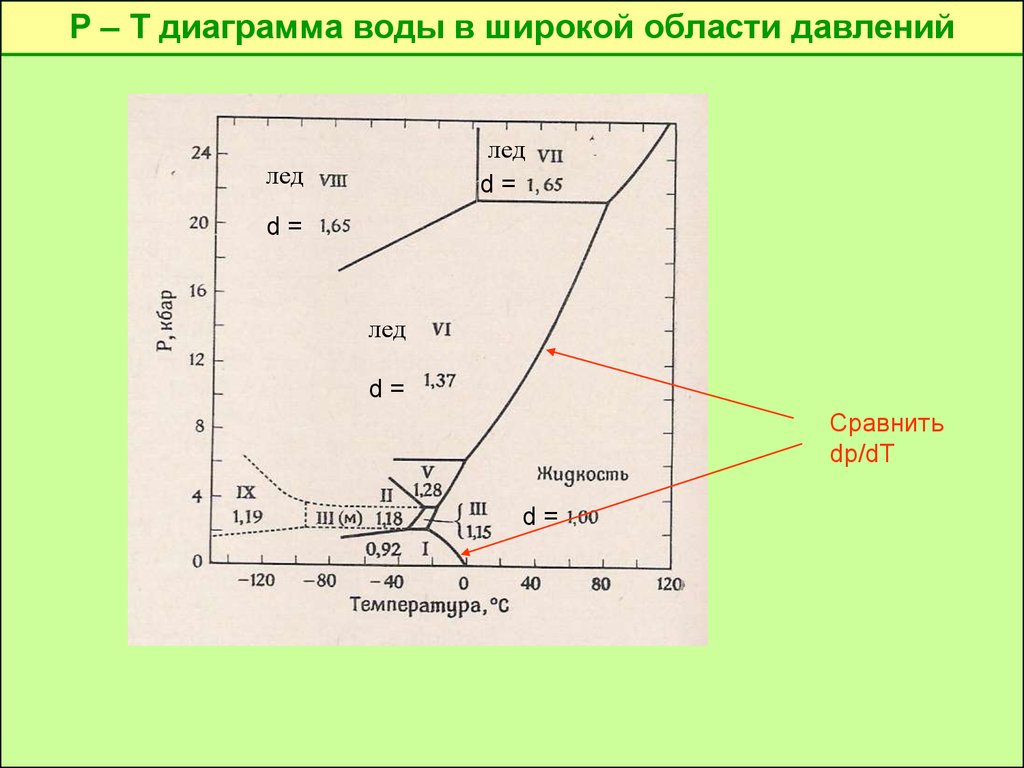
P – T диаграмма воды в широкой области давленийлед
d=
лед
d=
лед
d=
Сравнить
dp/dT
d=
25.
P –V – T Диаграмма состояния воды при высоком давленииdp/dT>0
dp/dT <0
26.
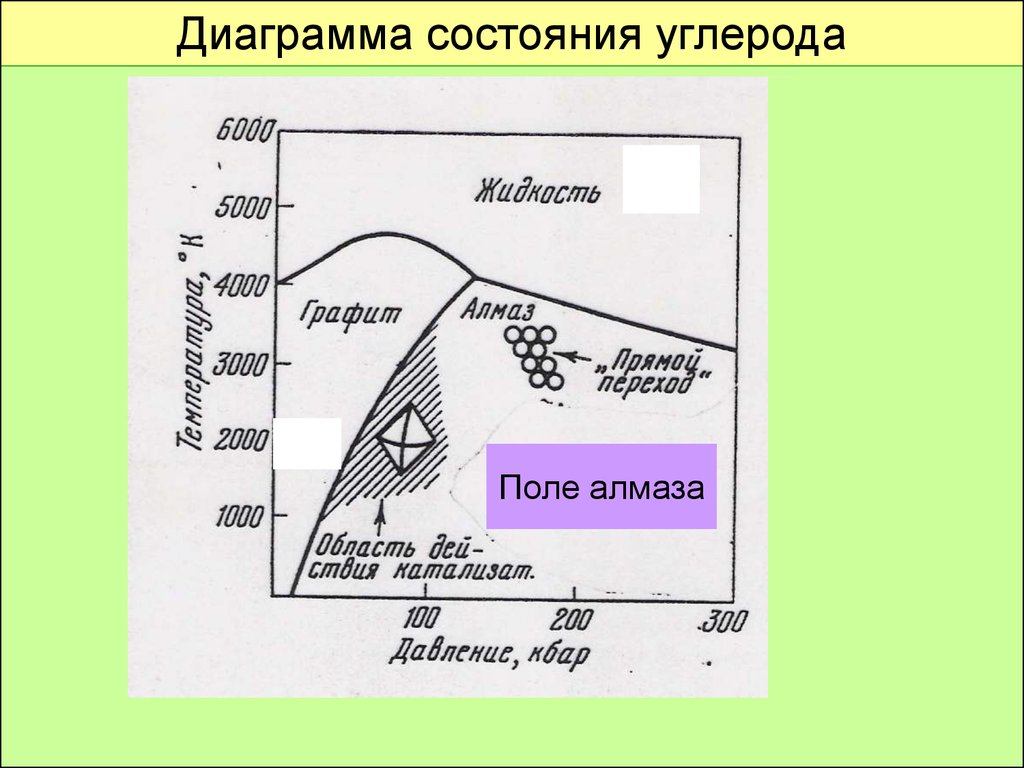
Диаграмма состояния углеродаПоле алмаза
27.
Диаграмма состояния углеродаАлмаз
200
Поле алмаза
Р,
кбар
Расплав
300
100
Графит
1000
Т, К
6000
Алмаз более устойчив, чем графит при
P > 5,5 + 26,4•10-3 T (K), тыс. атм.
Уравнение Лейпунского (1939 г.)
28.
Цех установок ростаалмазов
Установка роста
алмазов
29.
Искусственные алмазыювелирного качества
30.
Синтетические алмазы используются в бурении горных пород, металлообработке.Алмазные полировочные пасты
31. Разновидности графитовых материалов
32.
Новые неравновесные высокодисперсные формы углеродаФуллерены
Однослойная нанотрубка
Многослойная нанотрубка
С60
С240
С540
С60 @ С240@ С540
33.
Как и почему образуются нанотрубки?Углерод
Графит(в обычных условиях)
sp2 гибридизация: плоские сетки
Алмаз (высокие Т и Р)
sp3 гибридизация : кубическая стр-ра
графит
Алмаз
Нанотрубки/Фуллерены (в некоторых условиях)
sp2 + sp3
нанотрубка
С60
фуллерен
Оборванные связи на краях графеновых слоев повышают энергию слоя.
Сворачивание слоев устраняет оборванные связи и снижает общую
энергию системы.
34.
Фазовая диаграмма нитрида бора BN (аналог углерода).Р,
Кбар
200
BN
150
расплав
куб
100
50
Область
Самопроизвольного
перехода
BN
гексаг.
1000 2000 3000 4000
Температура, К
Область превращения
при действии катализаторов
35.
Кубический нитрид бора – высокотвердый материал для режущих инструментовBN, в отличие от
алмаза, инертен по
отношению к Fe и
поэтому может
быть использован
для
высокоскоростной
обработки черных
металлов (сталей и
чугунов).
36.
Двухкомпонентные(бинарные)
системы
37.
Классификация равновесий в бинарных системахпо признаку вариантности (Р=const)
Конгруэнтные
Инконгруэнтные
2-фазные
1. Изоморфные смеси с
экстремумом на
кривой равновесия
f =1 +1 –2 =0
в равновесии
А) жидкость – пар
Б) жидкость – тв. раствор
В) тв. раствор 1-тв. раствор 2
2. Конгруэнтное
плавление
(испарение, сублимация)
химических соединений
Изоморфные смеси
без экстремума
на кривой равновесия
f =2 +1 –2 =1
в равновесии
А) жидкость – пар
Б) жидкость – тв. раствор
В) тв. раствор 1-тв. раствор 2
3-фазные
f =2 +1 –3 =0
В равновесии комбинации фаз в
различных
агрегатных
состояниях:
Ж – Тв – Г
1,2,3
1,2,3
А) при охлаждении
1
2+3
Б) при охлаждении
2+3
1
38.
Топологическая взаимосвязь диаграмм состоянияодно- и двухкомпонентных систем
А Состав, мол.% В В
39.
Условно-моновариантные процессы при различных агрегатных состоянияхфаз-участников (при Р=const)
Ликвидус
Солидус
Т, оС
Кривая испарения
Т, оС
ПАР
Расплав
2
фазы
2
фазы
Твердый
раствор
А
Мол.% компонента В
Плавление –
кристаллизация
изоморфных смесей
Кривая
конденсации
Раствор
В
А
А
Мол.% компонента В
В
Мол.% компонента В
В
Испарение –
конденсация
изоморфных смесей
f=2+1– 2=1
40.
Моновариантный процесс кристаллизации изоморфных смесей. 1Т,
оС
Фигуративная
точка системы
ТВ,плавл.
Расплав
Ликвидус
2
фазы
Солидус
ТА,
плавл.
Твердый
раствор
х
0 10 20 30 40 50 60 70 80 90 100
А
Мол.% компонента В
В
41.
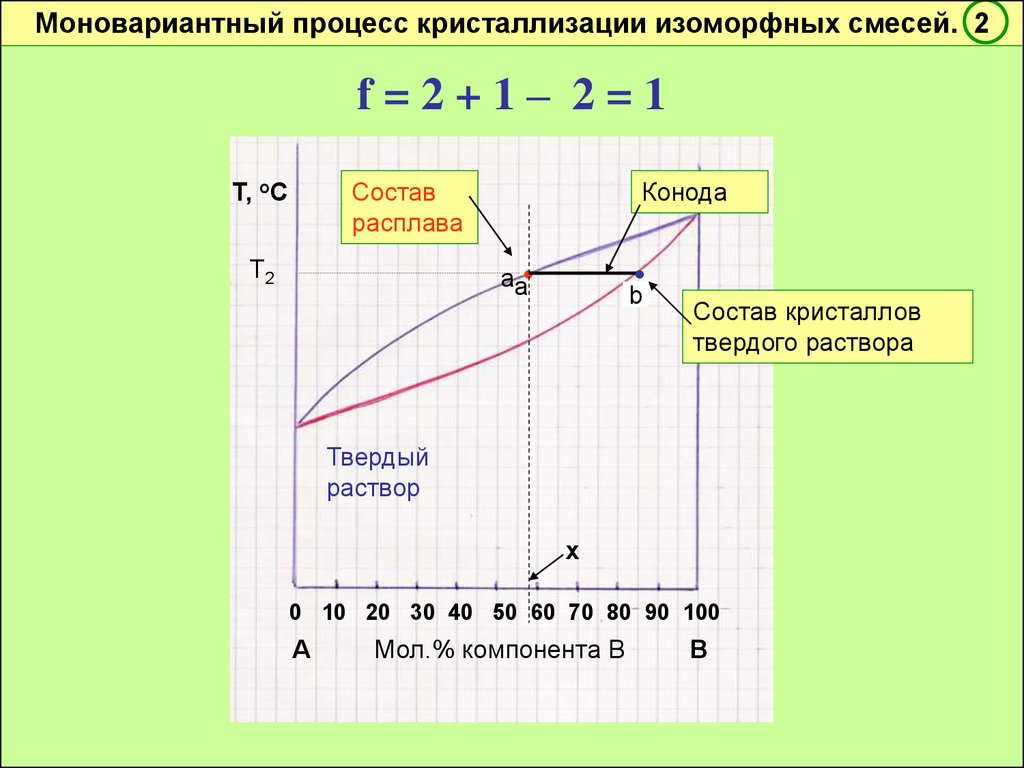
Моновариантный процесс кристаллизации изоморфных смесей. 2f=2+1– 2=1
Т, оС
Состав
расплава
Т2
Конода
aа
b
Состав кристаллов
твердого раствора
Твердый
раствор
х
0 10 20 30 40 50 60 70 80 90 100
А
Мол.% компонента В
В
42.
Моновариантный процесс кристаллизации изоморфных смесей. 3f=2+1– 2=1
Т, оС
Состав
расплава
Т3
a1
Конода
x
b1
Состав кристаллов
твердого раствора
Твердый
раствор
х
0 10 20 30 40 50 60 70 80 90 100
А
Мол.% компонента В
В
43.
Моновариантный процесс кристаллизации изоморфных смесей. 4f=2+1– 2=1
Т, оС
Состав
расплава
Т3
a1
Конода
x
b1
Состав кристаллов
твердого раствора
ν
ν
Твердый
раствор
х
=
0 10 20 30 40 50 60 70 80 90 100
А
Мол.% компонента В
В
расплава
тв.раствора
xb1
a1x
=
44.
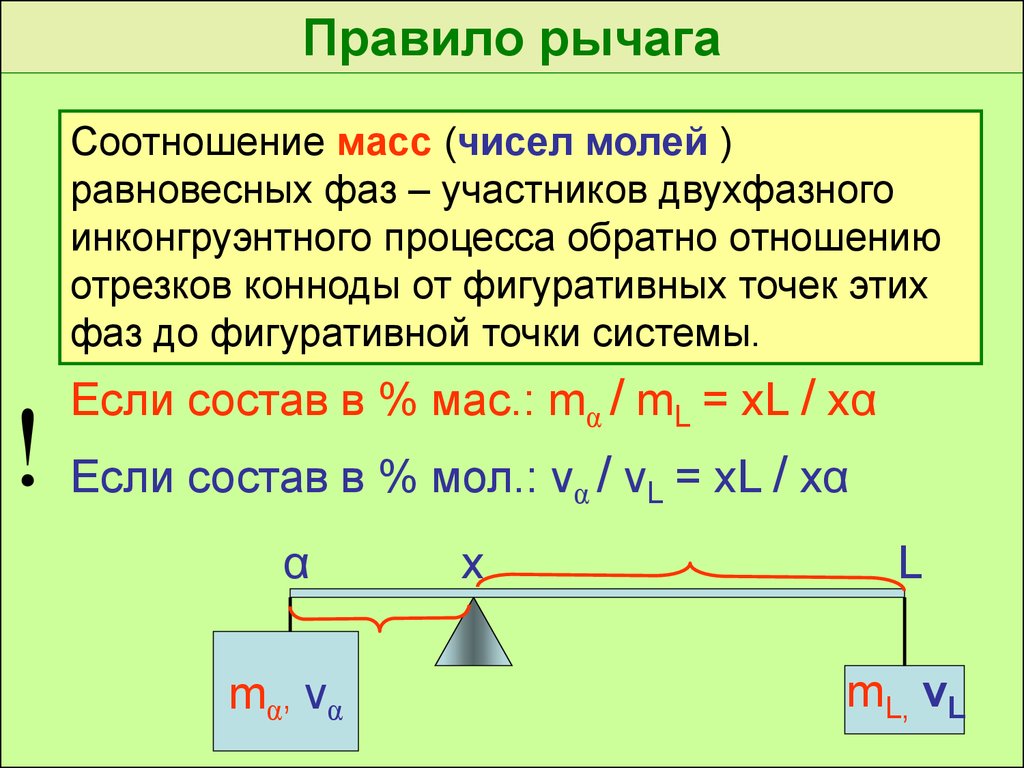
Правило рычагаСоотношение масс (чисел молей )
равновесных фаз – участников двухфазного
инконгруэнтного процесса обратно отношению
отрезков конноды от фигуративных точек этих
фаз до фигуративной точки системы.
Если состав в % мас.: mα / mL = xL / xα
! Если состав в % мол.: ν / ν = xL / xα
α
α
mα, να
х
L
L
mL, νL
45.
Моновариантный процесс кристаллизации изоморфных смесей. 5f=2+1– 2=1
Т, оС
Состав
расплава
Т4
a2
x
b2
Состав кристаллов
твердого раствора
Твердый
раствор
х
0 10 20 30 40 50 60 70 80 90 100
А
Мол.% компонента В
В
46.
Моновариантный процесс кристаллизации изоморфных смесей. 6f=2+1– 2=1
Т, оС
Состав
расплава
Т5
•a3
x
• b3
Состав кристаллов
твердого раствора
Твердый
раствор
х
0 10 20 30 40 50 60 70 80 90 100
А
Мол.% компонента В
В
47.
Инконгруэнтные превращенияв изоморфных смесях
f=2+1– 2=1
Условно моновариантное превращение.
Смысл моновариантности (f = 1):
1. Состав обеих равновесных фаз однозначно
определяется температурой. Для определения
состава фаз надо провести конноду при выбранной
температуре.
2. Данный состав фазы может быть реализован
только при вполне определенной температуре.
Этому составу равновесна вторая фаза также
вполне определенного состава.
48.
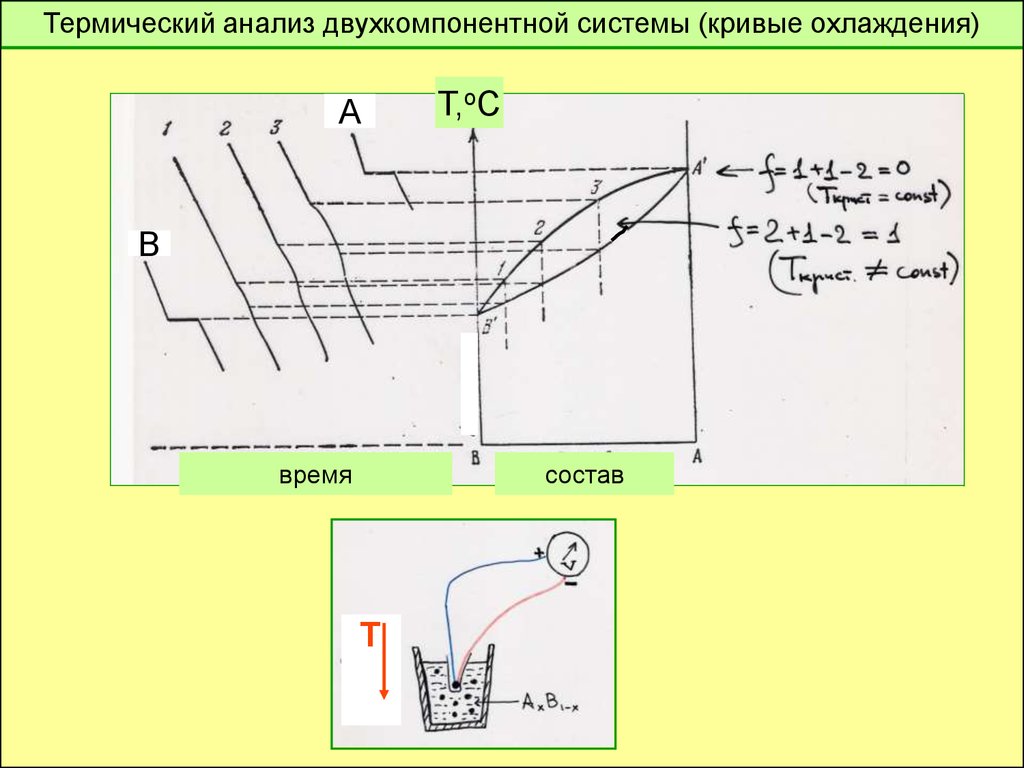
Термический анализ двухкомпонентной системы (кривые охлаждения)А
Т,оС
В
время
состав
Т
49.
Термодинамическоеобоснование
вида бинарных
диаграмм с
изоморфными смесями.
50.
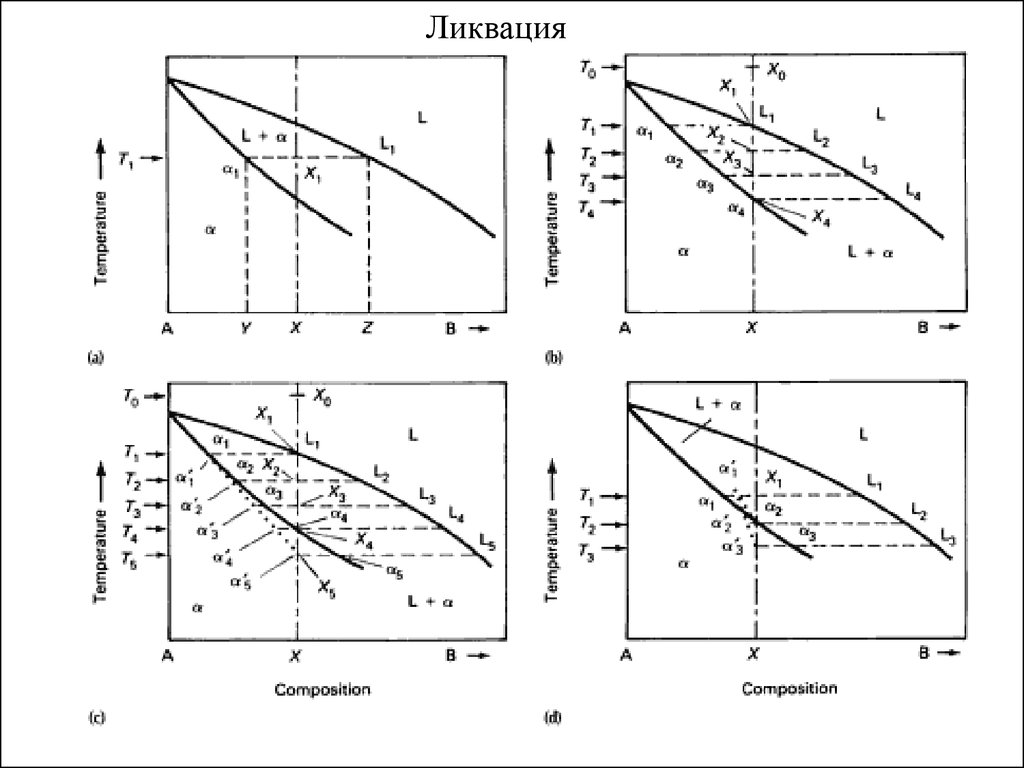
Моновариантный процесс при реальныхскоростях охлаждения расплавов: ликвация.
А
х
мол% В
51.
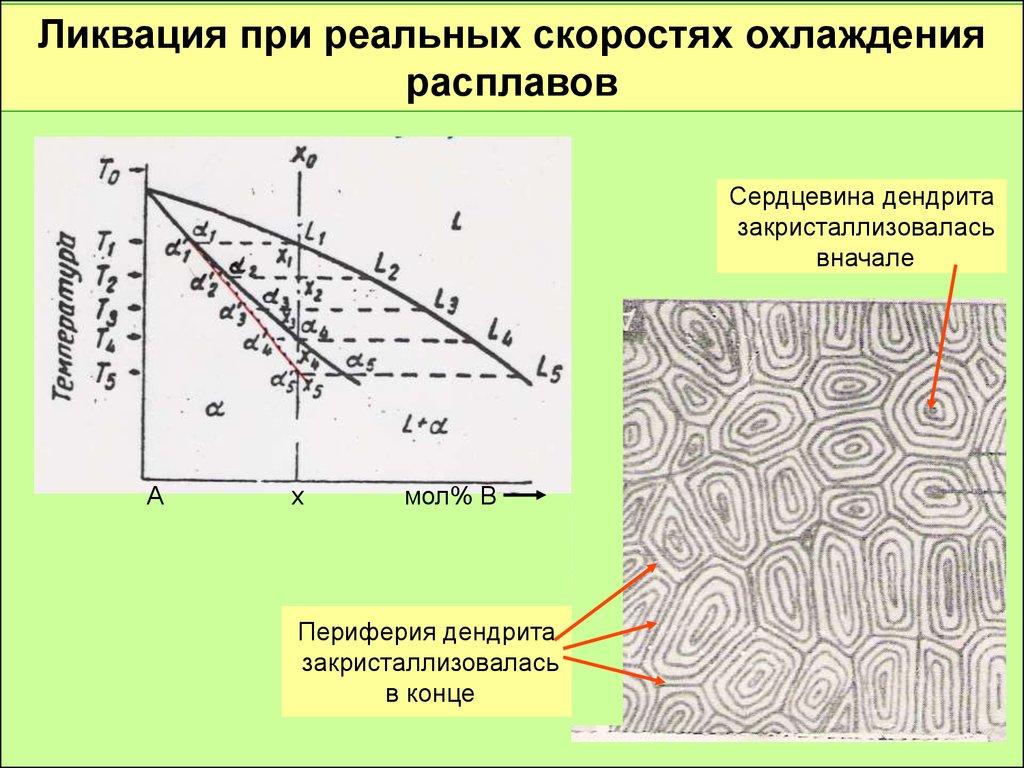
Ликвация при реальных скоростях охлаждениярасплавов
Сердцевина дендрита
закристаллизовалась
вначале
А
х
мол% В
Периферия дендрита
закристаллизовалась
в конце
52.
Диффузионный отжиг ликвидирует последствияликвации
Микроструктура сплава Ni0,7Cu0,3 . Увеличение 100
Обогащено
Cu
Обогащено
Ni
До отжига
После отжига
53.
При ликвации остатки расплава сохраняются доT < T равновесного солидуса.
При нагреве сплавов, подвергшихся ликвации,
расплав появляется при T < T равновесного
солидуса.
Горячеломкость сплавов – следствие ликвации в
процессе кристаллизации.












































 physics
physics chemistry
chemistry








