Similar presentations:
Физико-химические основы получения лекарственных препаратов. Лекция 2
1. Физико-химические основы получения лекарственных препаратов
Лекция: Физико-химический анализ.Диаграммы состояния бинарных систем.
Диаграммы «температура-состав» и
«давление-состав» для неограниченно
смешивающихся жидкостей. Закон Рауля.
Пасека Александра Евгеньевна
2. План лекции
I. Основные понятия и определенияII. Физико-химический анализ:
1. Принципы исследования и построения диаграмм состояния
1) принцип непрерывности
2) принцип соответствия:
III. Двухкомпонентные (бинарные) системы
Применение правила фаз Гиббса;
Метод термического анализа;
Метод построения кривых охлаждения;
Построение диаграммы плавкости двухкомпонентной системы по кривым
охлаждения;
Типы диаграмм состояния двухкомпонентных систем;
Анализ диаграммы состояния системы с простой эвтектикой. Правило рычага.
IV. Взаимная растворимость жидкостей:
1. Классификация жидкостей по взаимной растворимости;
2. Жидкие смеси с неограниченной растворимостью компонентов,
подчиняющиеся закону Рауля (идеальные смеси)
Диаграмма «давление-состав». Первый закон Коновалова.
2
Диаграмма «температура-состав»: анализ диаграмм.
3. Компетенции
УК-1, ОПК-1, ПКР - 1Знать:
физико- химическую сущность процессов, происходящих при фазовых
переходах в двухкомпонентных системах;
Уметь:
описывать состав и свойства диаграмм состояния двухкомпонентных систем;
применять правило фаз Гиббса для описания фазовых переходов;
Владеть:
Навыками построения и описания свойств диаграмм: «давление-состав»,
«температура-состав» двухомпонентных систем.
3
4. Физико-химический анализ
Диаграмма – совокупность геометрических элементов (точек,линий, плоскостей и т.д.), которые изображают связь между
параметрами, определяющими состояние системы и ее составом.
Диаграмма – графическое изображение зависимостей р от Т или
р от состава и Т от состава.
Для построения фазовых диаграмм используют метод физикохимического анализа.
В
основе физико- химического анализа лежит изучение
функциональной зависимости между значениями какого-либо
физического свойства системы и факторами, определяющими ее
равновесие.
4
5. Физико-химический анализ
56. Физико-химический анализ
Исследование и построение диаграмм состояния основано направилах:
принципе непрерывности и
принципе соответствия.
1. Принцип непрерывности: при непрерывном изменении
параметров, определяющих состояние системы (давление,
температура и др.), свойства ее отдельных фаз изменяются также
непрерывно до тех пор, пока не изменится число или природа ее
фаз.
При появлении новых или исчезновении существующих фаз
свойства системы изменяются скачком.
6
7. Физико-химический анализ
2. Принцип соответствия: на диаграмме состояния каждойфазе или каждому комплексу равновесных фаз соответствует
определенный геометрический образ (плоскость, кривая, точка и
т.д.).
Часть плоскости, называемую полем фазы, изображает область
существования фазы в определённом состоянии (т, г, ж).
Линии пересечения плоскостей характеризуют равновесное
состояние (ж↔п, ж↔т, т↔п). Точка на диаграмме состояния
(фигуративная точка) показывает значение параметров,
характеризующих данное состояние системы.
7
8. Двухкомпонентные (бинарные) системы. Равновесия: Т1 ⇄ Т2, Ж ⇄ Т, Ж⇄Ж, Ж⇄ П
Применение правила фаз ГиббсаС=К–Ф+n
Если К = 2, а на состояние равновесия влияют температура и
давление, то
С = 2 –Ф+ 2 = 4 – Ф.
Ф = 4, если Сmin= 0, поэтому в двухкомпонентной системе число
фаз, одновременно находящихся в равновесии, не может быть
больше 4 (Ж, П, Т1, Т2).
Если Фмин. = 1, то Смaкс.=3, а это температура, давление и
концентрация одного из компонентов.
8
9. Двухкомпонентные (бинарные) системы.
Метод термического анализа (термография) – совокупностьэкспериментальных методов определения температуры, при которой
в равновесной системе изменяется число фаз.
Сущность метода термического анализа:
процессы, протекающие в веществе и сопровождающиеся тепловым
эффектом, приводят к появлению изотермических остановок или
изменения угла наклона кривой температура – время.
Различают:
визуальный термический анализ (простая термография)
термический анализ, основанный на построении
охлаждения (дифференциальная термография).
кривых
10. Двухкомпонентные (бинарные) системы.
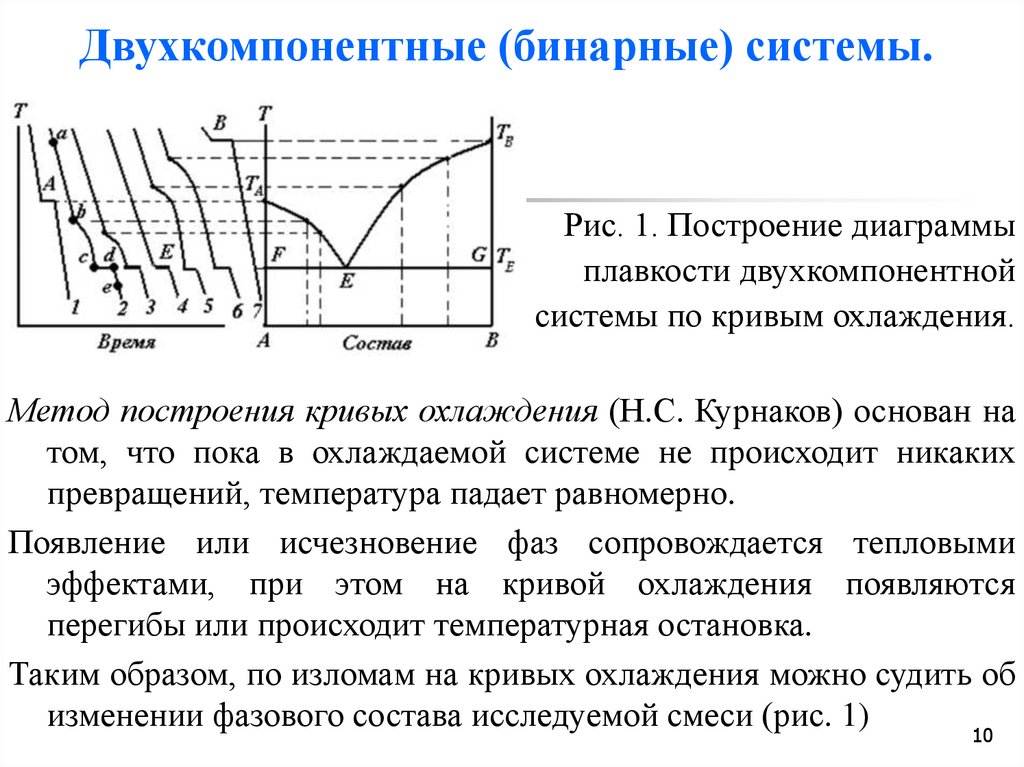
Рис. 1. Построение диаграммыплавкости двухкомпонентной
системы по кривым охлаждения.
Метод построения кривых охлаждения (Н.С. Курнаков) основан на
том, что пока в охлаждаемой системе не происходит никаких
превращений, температура падает равномерно.
Появление или исчезновение фаз сопровождается тепловыми
эффектами, при этом на кривой охлаждения появляются
перегибы или происходит температурная остановка.
Таким образом, по изломам на кривых охлаждения можно судить об
изменении фазового состава исследуемой смеси (рис. 1)
10
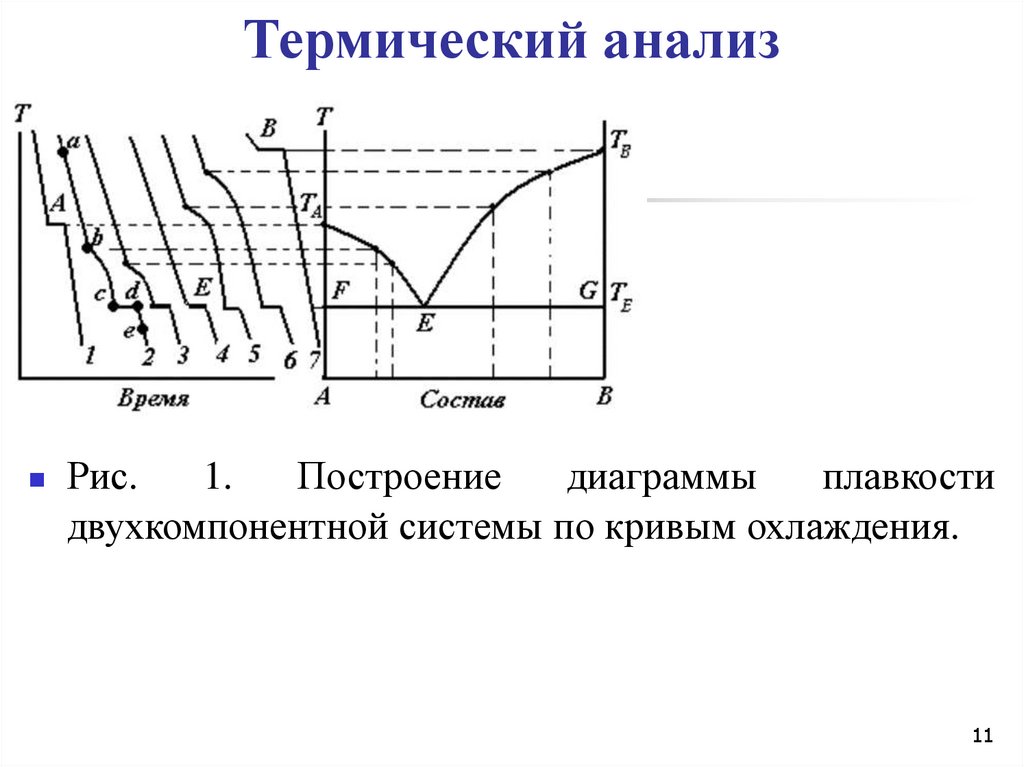
11. Термический анализ
Рис.1.
Построение
диаграммы
плавкости
двухкомпонентной системы по кривым охлаждения.
11
12. Термический анализ
Охлаждение чистого расплавленного вещества (кривая 1, рис. 1)вызовет температурную остановку при его кристаллизации.
Выделяющаяся скрытая теплота кристаллизации компенсирует
отвод теплоты в окружающую среду.
На кривой охлаждения появляется горизонтальный участок.
Размер
горизонтального
участка,
т.е.
длительность
температурной остановки, зависят от количества вещества, от
скорости охлаждения системы.
Состав жидкой фазы при кристаллизации чистого вещества не
изменяется, поэтому температура кристаллизации постоянна.
Подобную кривую охлаждения дает смесь эвтектического
12
состава (кривая 4).
13. Термический анализ
В случае охлаждения смесей различного состава (кривые 2, 3, 5, 6) доначала кристаллизации температура падает со временем практически
линейно (участок ab, кривая 2).
Смесь в отличие от чистого вещества, кристаллизуется не при
постоянной
температуре
(хотя
процесс
также
является
экзотермическим), а в некотором температурном интервале, т.к. при
выделении кристаллов одного из компонентов смесь обогащается
вторым, и температура ее кристаллизации понижается.
На кривых охлаждения при температуре начала кристаллизации (точка
b, кривая 2) происходит излом кривой, так как скорость охлаждения
уменьшается в результате выделения теплоты кристаллизации (участок
13
bc, кривая 2).
14. Термический анализ
Температура падает, пока состав сплава (смеси) не станетэвтектическим (точка c).
С этого момента кристаллизуется эвтектика (мелкозернистая
смесь кристаллов двух компонентов) при постоянной
температуре (участок cd).
В точке d расплав полностью исчезает и начинается
охлаждение твердых фаз (участок de).
Точки А, В на диаграмме соответствуют 100%-ному
содержанию компонентов А и В. Отсчет содержания компонента
14
В начинается от точки А, где его содержание составляет 0%.
15. Значение фазовых диаграмм для фармации
Для устранения «несовместимости физической» (отсыреваниепорошков, расслоение эмульсий) и «несовместимости химической»
(взаимодействие между компонентами с образованием новых
соединений).
Физическая несовместимость связана с образование эвтектики.
Эвтектические смеси образуют анестезин с резорцином, антипирин с
фенацетином, ацетилсалициловая кислота с антипирином и др.
Образование эвтектической смеси может улучшать качество лекарств.
Изготовление присыпки из тимола и ментола приводит к образованию
эвтектической смеси, состоящей из более мелких частиц, чем смесь из
тех же веществ, но отличающаяся по составу от эвтектической. Это
приводит
к
равномерному
распределению
компонентов
в
лекарственной форме.
Диаграммы состояния лекарственных смесей помогают приготовить
суппозитории (медицинские свечи). Необходима такая жировая основа,
при которой свечи плавятся при температуре тела и не размягчаются
15
при t < 32°C.
16. Диаграммы состояния двухкомпонентных систем
Диаграммы состояния строят в координатах температура – состав поэкспериментальным данным.
Типы диаграмм состояния двухкомпонентных конденсированных
систем:
диаграмма с простой эвтектикой;
диаграмма с образованием устойчивого химического соединения
(конгруэнтно плавящимся);
диаграмма с образованием неустойчивого химического
соединения (инконгруэнтно плавящимся);
диаграмма с неограниченной взаимной растворимостью компонентов в
твердом состоянии;
диаграмма с ограниченной растворимостью компонентов в твердом
состоянии (I и II вида);
диаграмма с полиморфизмом компонентов
16
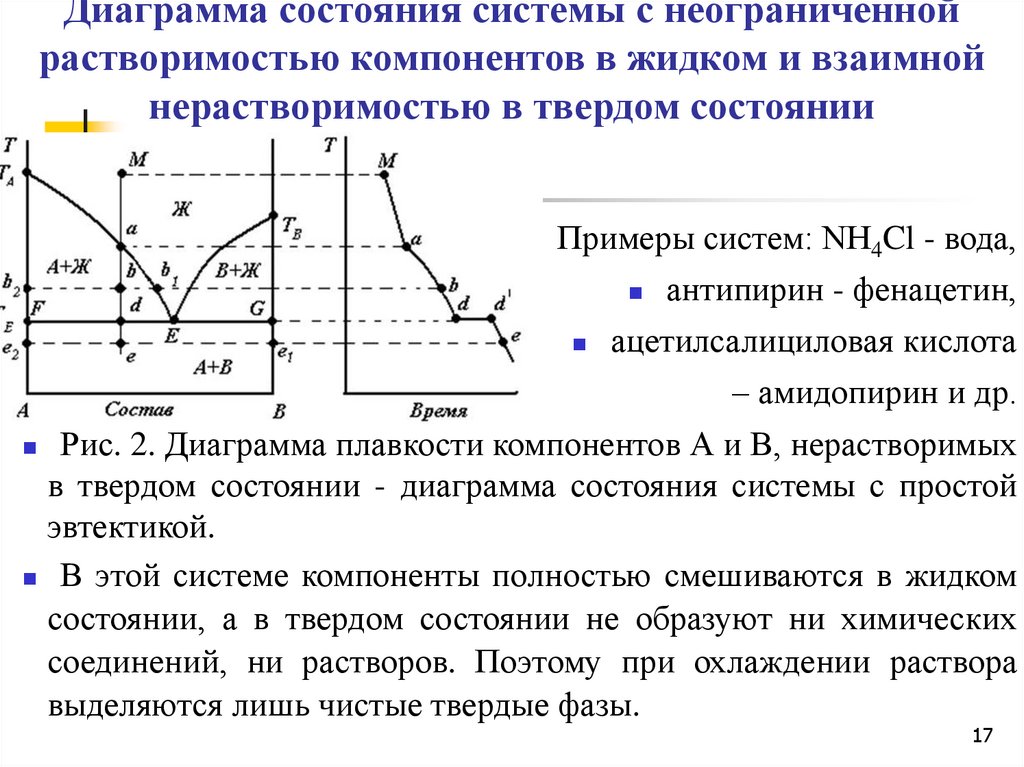
17. Диаграмма состояния системы с неограниченной растворимостью компонентов в жидком и взаимной нерастворимостью в твердом
состоянииПримеры систем: NH4Cl - вода,
антипирин - фенацетин,
ацетилсалициловая кислота
– амидопирин и др.
Рис. 2. Диаграмма плавкости компонентов А и В, нерастворимых
в твердом состоянии - диаграмма состояния системы с простой
эвтектикой.
В этой системе компоненты полностью смешиваются в жидком
состоянии, а в твердом состоянии не образуют ни химических
соединений, ни растворов. Поэтому при охлаждении раствора
выделяются лишь чистые твердые фазы.
17
18. Диаграмма состояния системы с простой эвтектикой.
Такие диаграммы образуются, когда компоненты А и Вo имеют разные типы кристаллических решеток и различные
размеры радиусов частиц решетки,
o при наличии одинакового типа решетки, но резко различных
радиусов частиц.
Любую фазовую диаграмму разбирают по плану:
1. Описать все поля, все характерные линии и точки.
2. Построить кривую охлаждения из точки заданного состава.
3. Для каждого участка кривой охлаждения применить правило
фаз Гиббса.
4. Определить состав всех соединений и записать их формулы.
5. Применить правило рычага к указанной точке.
18
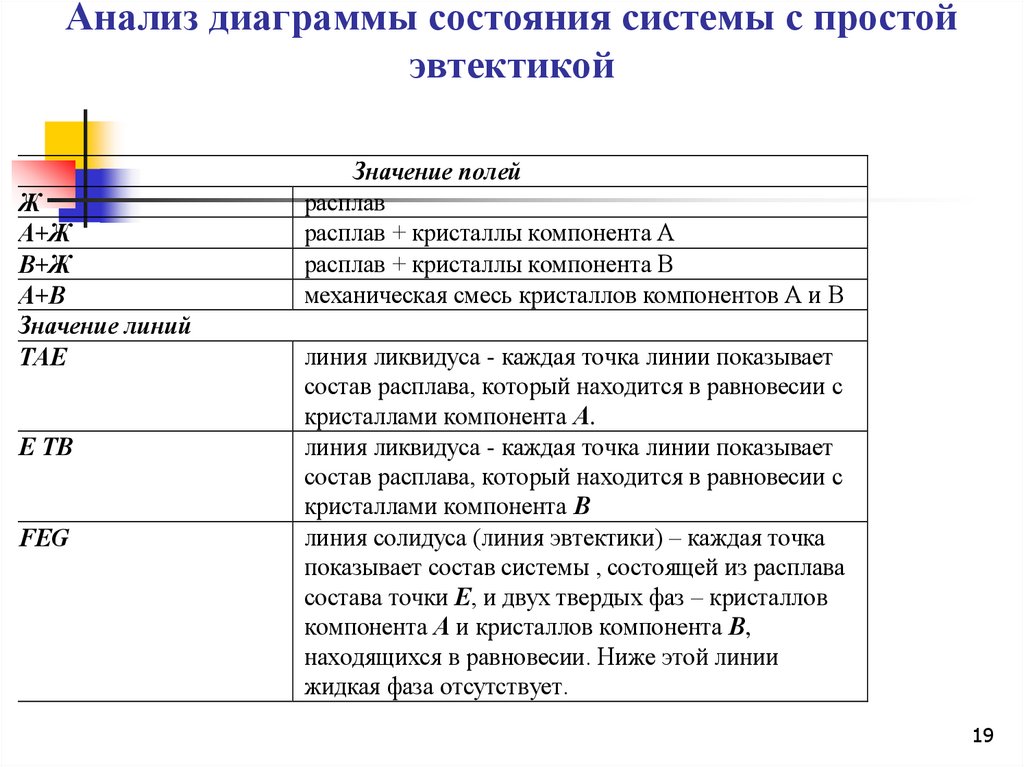
19. Анализ диаграммы состояния системы с простой эвтектикой
ЖА+Ж
В+Ж
А+В
Значение линий
ТАЕ
Е ТВ
FЕG
Значение полей
расплав
расплав + кристаллы компонента А
расплав + кристаллы компонента В
механическая смесь кристаллов компонентов А и В
линия ликвидуса - каждая точка линии показывает
состав расплава, который находится в равновесии с
кристаллами компонента А.
линия ликвидуса - каждая точка линии показывает
состав расплава, который находится в равновесии с
кристаллами компонента В
линия солидуса (линия эвтектики) – каждая точка
показывает состав системы , состоящей из расплава
состава точки Е, и двух твердых фаз – кристаллов
компонента А и кристаллов компонента В,
находящихся в равновесии. Ниже этой линии
жидкая фаза отсутствует.
19
20. Анализ диаграммы состояния системы с простой эвтектикой
ТАТВ
Е
ТЕ
Значение точек
температура
плавления
компонента А
температура
плавления
компонента В
точка эвтектики
температура эвтектики
Эвтектика – механическая смесь кристаллов двух компонентов,
обладающая самой низкой температурой кристаллизации.
Механическая смесь кристаллов компонентов А и В, которая
одновременно кристаллизуется при температуре ТЕ – твердая
эвтектика.
Точка Е пересечения кривых ТАЕ и ЕТВ показывает температуру и
состав расплава, который одновременно находится в равновесии с
кристаллами компонента А и компонента В – точка эвтектики.
Расплав, состав которого соответствует точки Е – эвтектический
20
расплав.
21. Анализ диаграммы состояния системы с простой эвтектикой
На линии эвтектики FЕG в равновесии находятся три фазы:расплав состава точки Е (LЕ );
кристаллы компонента А;
кристаллы компонента В.
По
достижении температуры эвтектики (ТЕ) наступает
эвтектическая реакция – из расплава выделяются кристаллы
обоих компонентов: А и В.
Линия, показывающая изменение состава жидкой фазы от
начала процесса охлаждения расплава до его полной
кристаллизации – путь кристаллизации (кривая Mаb1E).
21
22. Анализ диаграммы состояния системы с простой эвтектикой
Таблица 1. Результат рассмотрения процессаохлаждения расплава из точки М
Точка
М
а
b
d
е
Что происходит
Ф
С
Охлаждение расплава
1
2
2
1
Появляются
первые
кристаллы компонента А
Продолжают
выпадать
кристаллы компонента А,
состав расплава b1, состав
твердой фазы b2
Одновременно
кристаллизуются
компоненты А и В, на
кривой охлаждения участок
d-d´
Охлаждение механической
смеси компонента А состава
е2 и компонента В состава е1
Что означает число
степеней свободы
Можно
менять
температуру и состав
расплава
Можно менять только
температуру
2
1
Можно
менять
или
температуру или состав
расплава
3
0
Система инвариантна
2
1
Можно менять только
температуру
22
23. Анализ диаграммы состояния системы с простой эвтектикой
Определение количественных соотношений между фазами.Правило рычага
Коннода (нода) – соединительная линия двух сопряженных точек (изотерма).
Изоплета – линия постоянного состава.
Количественные соотношения между массами фаз гетерогенной системы
находят с помощью правила рычага.
Рис. 3. Фазовая диаграмма с эвтектикой
для определения содержания
компонентов по правилу рычага.
Точка К – ненасыщенный расплав состава g0.
Точка Р0, состава g0, отражает валовый
(общий) состав.
Точки Р1 состава g1 и Р2 состава g2 отражают
состав жидкой и твердой фаз
соответственно (сопряженные точки).
23
24. Анализ диаграммы состояния системы с простой эвтектикой
2425. Взаимная растворимость жидкостей
Растворы жидкости в жидкости – смеси.Смеси различаются по взаимной растворимости жидкостей,
что связано с природой последних и характером
межмолекулярного взаимодействия.
Жидкости по взаимной растворимости делят на три группы:
1. Жидкости, смешивающиеся друг с другом в любых
соотношениях (вода-этанол; бензол-толуол, этанол-метанол).
2. Жидкости, ограниченно растворяющиеся друг в друге
(вода-фенол, вода-анилин, вода-никотин, вода-диэтиламин и др.).
3. Жидкости практически нерастворимые друг в друге (водартуть, вода-бензол и др.).
25
26. Взаимная растворимость жидкостей
Жидкости первой группы делят на 3 типа:А. Идеальные жидкие растворы, подчиняющиеся закону Рауля.
Б.
Неограниченно
растворимые
жидкости
с
положительными и отрицательными отклонениями от
закона Рауля, но без максимума или минимума на кривой
зависимости давления насыщенного пара от состава раствора.
В. Неограниченно растворимые жидкости с максимумом или
минимумом на кривой зависимости давления насыщенного
пара от состава раствора.
26
27. Жидкие смеси с неограниченной растворимостью компонентов
Смеси, подчиняющиеся закону Рауля (идеальные смеси):давление и состав пара
1. Исходные условия. а) Будем считать, что жидкости
I. неограниченно растворимы друг в друге и
II. обе являются летучими, т. е. дают над раствором пар.
б) 1 — менее летучая жидкость, 2 — более летучая, т.е. у первой
жидкости — ниже давление насыщенного пара над чистым
веществом и, соответственно, выше температура кипения:
в) в идеальных растворах все виды межмолекулярных
взаимодействий в системе — 1–1, 2–2 и 1–2 — одинаковы по
характеру и силе. Примеры: бензол–толуол, гексан–гептан,
27
метанол–этанол.
28. Смеси, подчиняющиеся закону Рауля (идеальные смеси)
2. а) Для идеальной смеси закон Рауля применим к обоим летучимкомпонентам:
(3)
(4)
б) общее давление пара над смесью линейно зависит от состава
смеси.
Это изображено на рис. 4, где
- по оси абсцисс отложена мольная доля в жидкой фазе более
летучего компонента,
- пунктирными линиями показаны парциальные давления паров
каждого из двух компонентов (при разном составе смеси)
- и сплошной линией — общее давление пара над раствором.
29. Рис. 4. Зависимость общего и парциального давления пара идеального бинарного раствора от состава.
Из изотермы на диаграмме (рис.4) видно, что:1.Каждый из летучих компонентов имеет
наибольшее давление насыщенного пара над
чистой жидкостью.
2. Общее давление насыщенного пара над
раствором есть величина аддитивная: Робщ. = Р1 + Р2.
3. Понижение мольной доли компонента в растворе приводит к
понижению его парциального давления в паре.
4. Увеличение содержания более летучего компонента 2 в растворе
повышает общее давление над раствором и, следовательно,
понижает температуру кипения раствора.
5. Состав жидкого раствора не совпадает с составом пара над ним: в
парах всегда содержится больше более летучего компонента.
30. Рис. 4. Зависимость общего и парциального давления пара идеального бинарного раствора от состава.
3. а) Определим состав пара при томили ином составе жидкой фазы. Мольные доли
каждого вещества в паре обозначим штрихом.
Тогда, например, доля в паре второго компонента
такова:
(5-6).
(7)
Т.к. по условию, первый компонент является менее летучим.
б) Заметим: так как X1 + X2 = 1, то знаменатель выражения (6)
меньше единицы:
(8).
в) Доля второго (более летучего) компонента в паре выше, чем в
жидкой смеси. Первый закон Коновалова: по сравнению с жидкой
фазой, состав газовой фазы обогащен более летучим компонентом.
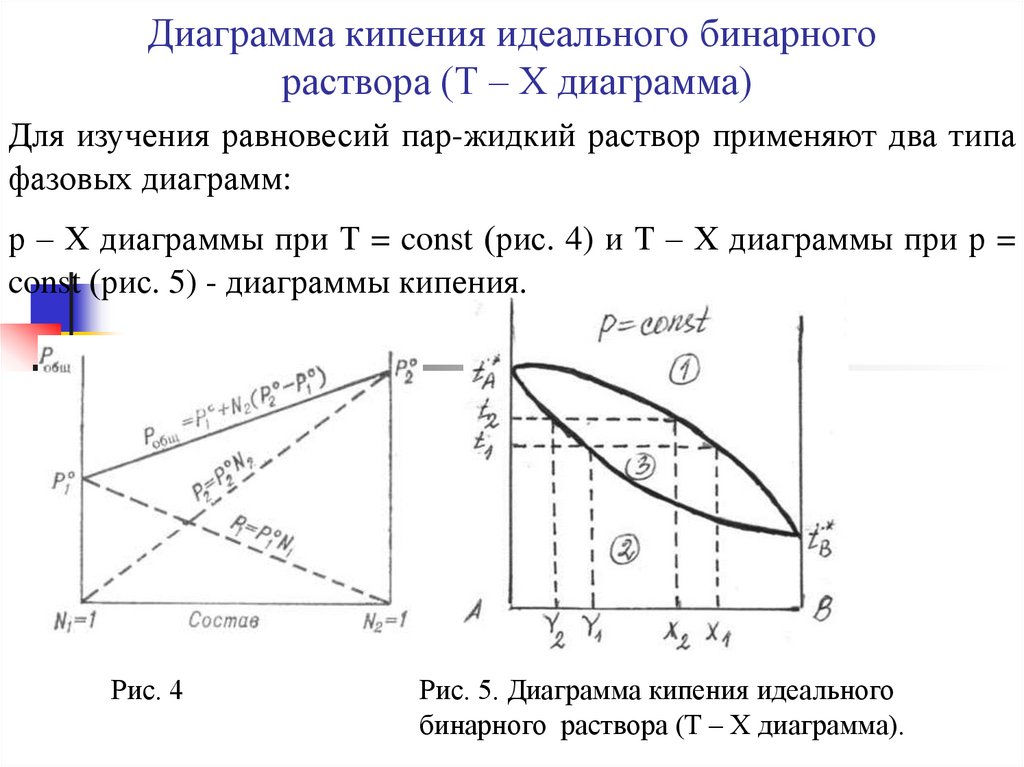
31. Диаграмма кипения идеального бинарного раствора (Т – Х диаграмма)
Для изучения равновесий пар-жидкий раствор применяют два типафазовых диаграмм:
р – Х диаграммы при Т = const (рис. 4) и Т – Х диаграммы при р =
const (рис. 5) - диаграммы кипения.
Рис. 4
Рис. 5. Диаграмма кипения идеального
бинарного раствора (Т – Х диаграмма).
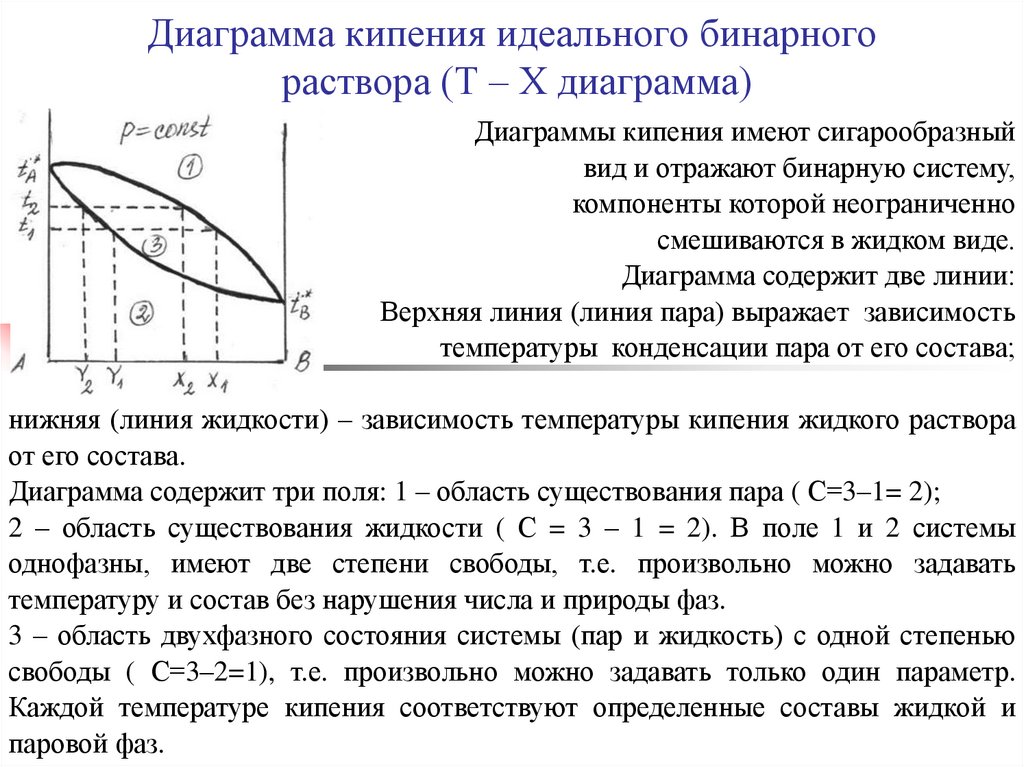
32. Диаграмма кипения идеального бинарного раствора (Т – Х диаграмма)
Диаграммы кипения имеют сигарообразныйвид и отражают бинарную систему,
компоненты которой неограниченно
смешиваются в жидком виде.
Диаграмма содержит две линии:
Верхняя линия (линия пара) выражает зависимость
температуры конденсации пара от его состава;
нижняя (линия жидкости) – зависимость температуры кипения жидкого раствора
от его состава.
Диаграмма содержит три поля: 1 – область существования пара ( С=3–1= 2);
2 – область существования жидкости ( С = 3 – 1 = 2). В поле 1 и 2 системы
однофазны, имеют две степени свободы, т.е. произвольно можно задавать
температуру и состав без нарушения числа и природы фаз.
3 – область двухфазного состояния системы (пар и жидкость) с одной степенью
свободы ( С=3–2=1), т.е. произвольно можно задавать только один параметр.
Каждой температуре кипения соответствуют определенные составы жидкой и
паровой фаз.
33. Список литературы
1. Физическая химия: учебник / Ю.Я. Харитонов. – М.: ГЭОТАР - Медиа,2013. – 608 с. http://www.studentlibrary.ru/book/ISBN9785970423 905.html
2. Мушкамбаров Н.Н., Физическая и коллоидная химия: учебник для
медицинских вузов (с задачами и решениями) [Электронный ресурс]
учебник для медицинских вузов (с задачами и решениями). /
Мушкамбаров Н.Н. - 4-е изд., стер. - М. : ФЛИНТА, 2015. - 455 с.:
http://www.studentlibrary.ru/book/ISBN97859976522954.html
3. Л.С. Анисимова, Н.П. Пикула, Е.В. Михеева, ПРАКТИКУМ ПО
ФИЗИЧЕСКОЙ И КОЛЛОИДНОЙ ХИМИИ. Учебное пособие для
студентов ИГНД очного и заочного обучения. - Издательство ТПУ, Томск,
2007.




























 chemistry
chemistry








