Кодирование чисел

1.

Кафедра «Автоматизированные станочные системы»
Dept. of Automated Manufacturing Systems
Кодирование чисел.
Код Хэмминга
Лекция 6
Троицкий Д.И. Информатика САПР 1 семестр
1

2. Коды: прямой, обратный, дополнительный, модифицированный

Одним из способов выполнения операции вычитания
является
замена
знака
вычитаемого
на
противоположный и прибавление его к уменьшаемому:
A – B = A + (–B).
Этим операцию арифметического вычитания
заменяют операцией алгебраического сложения.
Последняя и становится основной операцией.
Для машинного представления отрицательных
чисел используют коды:
прямой,
обратный,
дополнительный,
модифицированный.
Троицкий Д.И. Информатика САПР 1 семестр
2

3. Коды: прямой, обратный, дополнительный, модифицированный

Прямой код обычно используется при хранении чисел в
запоминающем устройстве, а обратный и дополнительный
коды — при выполнении над числами арифметических и
некоторых других операций. При пересылках из
запоминающего устройства в арифметическое и обратно
числа перекодируются.
Все три кода состоят из кода знака (число отведённых
разрядов l), кода целой части (m) и кода дробной части (n)
числа. Сумма d =l+т+n называется длиной кода. Как
правило l, т и n фиксированы. В случае целых чисел n=0,
для правильных дробей обычно т=0, когда все числа
одного знака, l=0.
Для положительных чисел код знака обозначается
последовательностью нулей, для отрицательных —
последовательностью единиц. Для положительных чисел
прямой, обратный и дополнительный коды совпадают.
Троицкий Д.И. Информатика САПР 1 семестр
3

4. Прямой код числа

При кодировании прямым n-разрядным двоичным кодом
один разряд (как правило, самый старший) отводится
для знака числа. Остальные n-1 разрядов - для
значащих цифр. Значение знакового разряда равно 0
для положительных чисел, 1 - для отрицательных.
Пример: 1 = 0000 0001, -1 = 1000 0001.
Таким образом, прямой код положительного числа
совпадает
с
самим
числом,
а
прямой
код
отрицательного числа отличается от самого числа
единицей в старшем разряде.
Троицкий Д.И. Информатика САПР 1 семестр
4

5. Обратный код числа

Обратный код строится только для отрицательного числа.
Обратный код двоичного числа является инверсным
изображением самого числа, в котором все разряды
исходного числа принимают инверсное значение.
Пример:
А1 = 0,11010; [А1]обр = 011010 (без изменений);
А2 = -0,11010; [А2]обр = 100101.
Обратный код двоичного числа является дополнением
модуля числа до наибольшего числа без знака,
умещающегося в разрядную сетку, т.е. до величины 1,111…1.
Пример:
+1210=11002=0_1100(прямой)=0_0011(обратный)
-15.2510=-1111.012=1_1111.01(прямой)=1_0000.10(обр.)
Троицкий Д.И. Информатика САПР 1 семестр
5

6. Дополнительный код числа

Дополнительный код строится только для
отрицательного числа. Использование прямого
кода усложняет структуру компьютера. В этом
случае операция сложения двух чисел, имеющих
разные знаки, должна быть заменена на операцию
вычитания меньшей величины из большей и
присвоения результату знака большей величины.
Введение
дополнительного
кода
позволяет
заменить вычитание на обычное сложение, что
упрощает устройство процессора.
Троицкий Д.И. Информатика САПР 1 семестр
6

7. Дополнительный код числа

На
примере десятичного вычитания
двухразрядных чисел
предположим,
что
надо
выполнить
вычитание 84-32 /результат 52/. Дополним
32 до 100 /это «дополнение» равно 68/.
Затем
выполним
сложение
84+68
/результат 152/. Единица «уходит», потому
что
рассматриваются
двухразрядные
десятичные числа.
Таким
образом дополнительный код
является математическим дополнением до
основания системы счисления.
Троицкий Д.И. Информатика САПР 1 семестр
7

8. Дополнительный код числа

Дополнительный
код
отрицательного
числа
отличается от обратного кода тем, что после
замены цифр производится сложение результата с
d-paзрядным числом, все разряды которого, кроме
младшего, содержат нули, причём перенос из
старшего разряда при сложении не выполняется.
Например, число в двоичной системе счисления
равно +11,01. Пусть задано l=1, т=3, n=4; дополняя
целую и дробную части нулями, запишем число в
виде
+011,0100.
Прямой
обратный
и
дополнительный коды заданного числа одинаковы
0 011 0100.
Для отрицательного числа —11,01 прямой код
имеет вид 1011 0100, обратный код — 1 100 1011 и
дополнительный — 1 100 1100.
Троицкий Д.И. Информатика САПР 1 семестр
8

9. Модифицированный код

При сложении чисел, меньших единицы, может
получиться результат, по абсолютной величине
больший единицы, что ведет к искажению
результатов
вычислений.
Переполнение
разрядной сетки легко обнаружить, используя
модифицированный прямой, модифицированный
обратный
или
модифицированный
дополнительный
коды.
Отличие
модифицированных
кодов
от
обычных
заключается в том, что на изображение знака
числа
отводится
два
разряда.
“Плюс”
изображается двумя нулями, а ”минус” – двумя
единицами.
Например, обратные модифицированные коды
чисел А1 = 0,11010 и А = -0,11010 запишутся в
виде [А1]обр =Троицкий
00,11010;
[А2]обр = 11,00101.
Д.И. Информатика САПР 1 семестр
9

10. Систематические коды

Систематический код – код, содержащий в себе кроме
информационных, контрольные разряды.
В контрольные разряды записывается некоторая
информация об исходном числе. Поэтому можно
говорить,
что
систематический
код
обладает
избыточностью.
Понятие корректирующей способности кода обычно
связывают
с
возможностью
с
возможностью
обнаружения и исправления ошибки. Количественно
корректирующая способность кода определяется
вероятностью обнаружения или исправления ошибки.
На практике наибольшей является вероятность
искажения одного символа (разряда). Следовательно,
основное внимание нужно обратить на обнаружение и
исправление одиночной ошибки.
Троицкий Д.И. Информатика САПР 1 семестр
10

11. Систематические коды

Корректирующая
способность кода связана
также с понятием кодового расстояния.
Кодовое
расстояние
d(A,B)
кодовых
комбинаций А и В определяется как вес такой
третьей
кодовой
комбинации,
которая
получается сложением исходных комбинаций по
модулю 2.
Что такое «сложение по модулю»?
Троицкий Д.И. Информатика САПР 1 семестр
11

12.

Операция сложения по
модулю
Это операция арифметического сложения, при котором единица
переноса в старший разряд, если таковая образуется при
поразрядном сложении, отбрасывается. Обозначается эта операция
.
Пример. Сложить по модулю 2 двоичные числа 10 и 11.
Сложение выполним поразрядно:
1) разряд единиц: 0 1 = 1;
2) разряд десятков: 1 1 = 0 (единица в старшем разряде
теряется).
Таким образом, 102 112 = 012.
Троицкий Д.И. Информатика САПР 1 семестр
12

13.

Пример. Сложить по модулю 10 десятичные числа 59 и 152.
Сложение выполним поразрядно:
1) разряд единиц: 9 2 = 1;
2) разряд десятков: 5 5 = 0;
3) разряд сотен: 0 1 = 1.
Таким образом, 59 152 =101.
Пример: кодовое расстояние между комбинациями 110101 и
010111 равно 100010.
110101
010111
_______
100010
Вес кодовой комбинации V(A) – количество единиц,
содержащихся в кодовой комбинации. V(100010)=2
Троицкий Д.И. Информатика САПР 1 семестр
13

14. Кодирование по методу четности-нечетности

Примером кода с обнаружением одной ошибки является код с
битом чётности. Конструкция его такова: к исходному слову
добавляется бит чётности. Если в исходном слове число
единичек чётно, то значение этого бита 0 (для контроля
нечетности - 1), если нечётно — 1 (для контроля нечетности 0). Таким образом, допустимые слова этого кода имеют
чётное количество единичек. Если получено слово с нечётным
(для контроля нечетности - четным) количеством единичек, то
при передаче произошла ошибка.
При этом допускается, что может возникнуть только одна
ошибка. В самом деле, для случая четности правильным
будет только половина возможных комбинаций. Чтобы одна
допустимая комбинация превратилась в другую, должно
возникнуть, по крайней мере, два нарушения или четное
число нарушений.
Троицкий Д.И. Информатика САПР 1 семестр
14

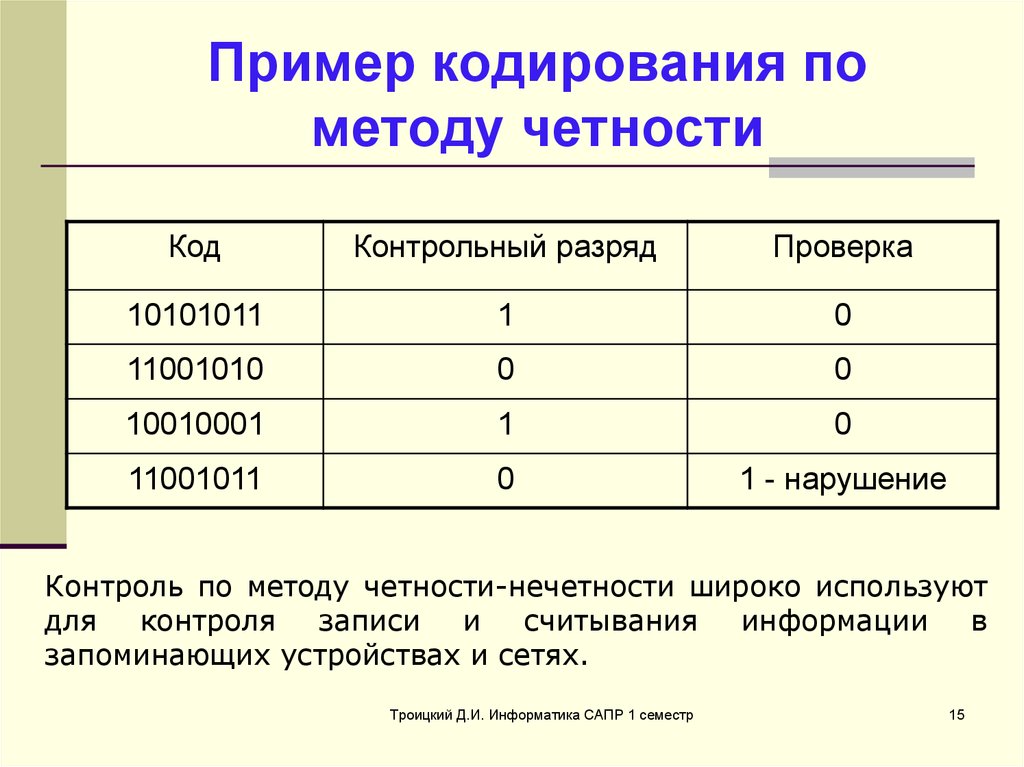
15. Пример кодирования по методу четности

Код
Контрольный разряд
Проверка
10101011
1
0
11001010
0
0
10010001
1
0
11001011
0
1 - нарушение
Контроль по методу четности-нечетности широко используют
для контроля записи и считывания информации в
запоминающих устройствах и сетях.
Троицкий Д.И. Информатика САПР 1 семестр
15

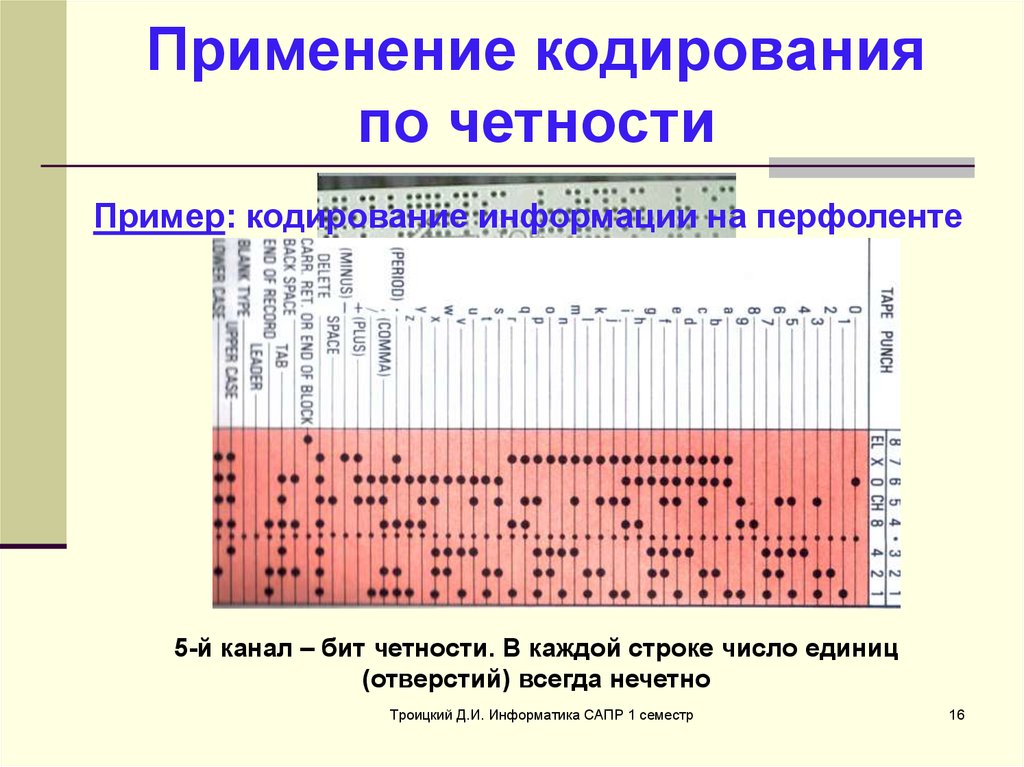
16. Применение кодирования по четности

Пример: кодирование информации на перфоленте
5-й канал – бит четности. В каждой строке число единиц
(отверстий) всегда нечетно
Троицкий Д.И. Информатика САПР 1 семестр
16

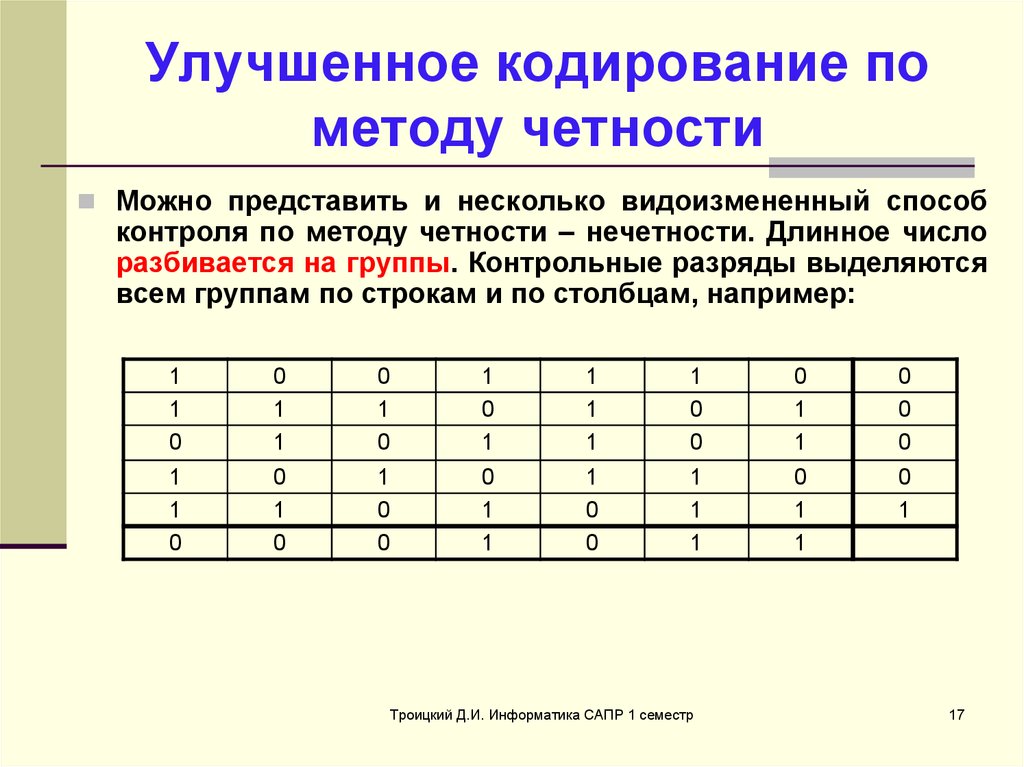
17. Улучшенное кодирование по методу четности

Можно представить и несколько видоизмененный способ
контроля по методу четности – нечетности. Длинное число
разбивается на группы. Контрольные разряды выделяются
всем группам по строкам и по столбцам, например:
1
1
0
0
1
1
0
1
0
1
0
1
1
1
1
1
0
0
0
1
1
0
0
0
1
1
0
0
1
0
1
0
0
0
1
1
1
0
0
1
1
1
0
1
1
0
1
Троицкий Д.И. Информатика САПР 1 семестр
17

18.

Увеличение избыточности информации приводит к тому,
что появляется возможность не только обнаружить
ошибку, но и исправить её.
Если произошла неисправность в каком-то из разрядов
числа, это приводит к тому, что при проверке на четность
сумма по соответствующим строкам и столбцам
изменится.
Следовательно, нарушение четности по этой строке и
столбцу можно зафиксировать, что в конечном счете
означает обнаружение не только самой ошибки, но и
места, где возникла ошибка.
Троицкий Д.И. Информатика САПР 1 семестр
18

19. Коды Хэмминга

Richard Hamming 1915-1998
Коды, предложенные американским ученым Р.
Хэммингом, обладают способностью не только
обнаружить, но и исправить одиночные ошибки.
Эти коды – систематические.
Обычно код Хэмминга описывается двумя
целыми числами, например, (11,7) и используется
при передаче 7-битных чисел. Такая запись
говорит, что при передаче 7-битного кода
используется 4 контрольных бита (7+4=11). При
этом предполагается, что имела место ошибка в
одном бите и что ошибка в двух или более битах
существенно менее вероятна. С учетом этого
исправление
ошибки
осуществляется
с
определенной вероятностью.
Троицкий Д.И. Информатика САПР 1 семестр
19

20. Коды Хэмминга

Рассмотрим пример передачи кода буквы s = 1110011
с использованием кода Хэмминга (11,7).
Позиция бита:
11 10 9 8 7 6 5 4 3 2 1
Значение бита:
1
1
1 * 0 0 1 * 1 * *
Символами * помечены четыре позиции, где
должны размещаться контрольные биты. Эти
позиции определяются целой степенью 2 (1, 2, 4,
8 и т.д.). Контрольная сумма формируется путем
выполнения операции сложения по модулю 2 над
кодами позиций ненулевых битов. В данном
случае это 11, 10, 9, 5 и 3.
Троицкий Д.И. Информатика САПР 1 семестр
20

21.

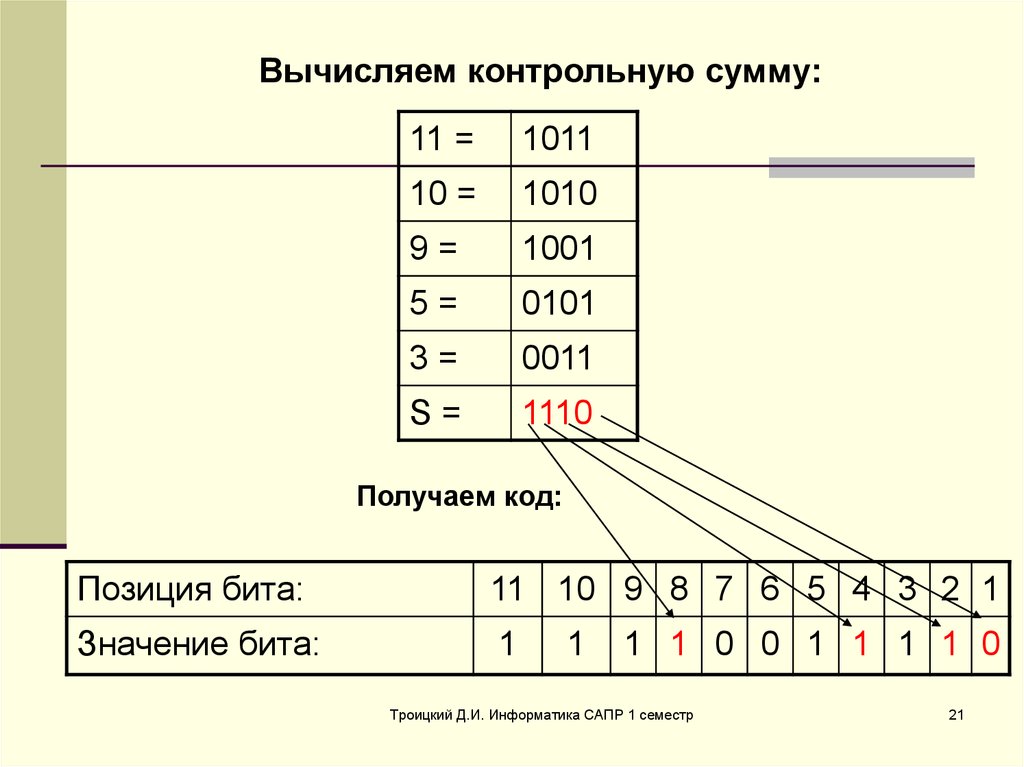
Вычисляем контрольную сумму:
11 =
1011
10 =
1010
9=
1001
5=
0101
3=
0011
S=
1110
Получаем код:
Позиция бита:
11 10 9 8 7 6 5 4 3 2 1
Значение бита:
1
1
1 1 0 0 1 1 1 1 0
Троицкий Д.И. Информатика САПР 1 семестр
21

22.

Просуммируем снова коды позиций ненулевых
битов (т.е. кроме 7, 6 и 1) и получим нуль.
11 =
1011
10 =
1010
9=
1001
8=
1000
5=
0101
4=
0100
3=
0011
2=
0010
S=
0000
Это значит, что данные переданы верно
Троицкий Д.И. Информатика САПР 1 семестр
22

23.

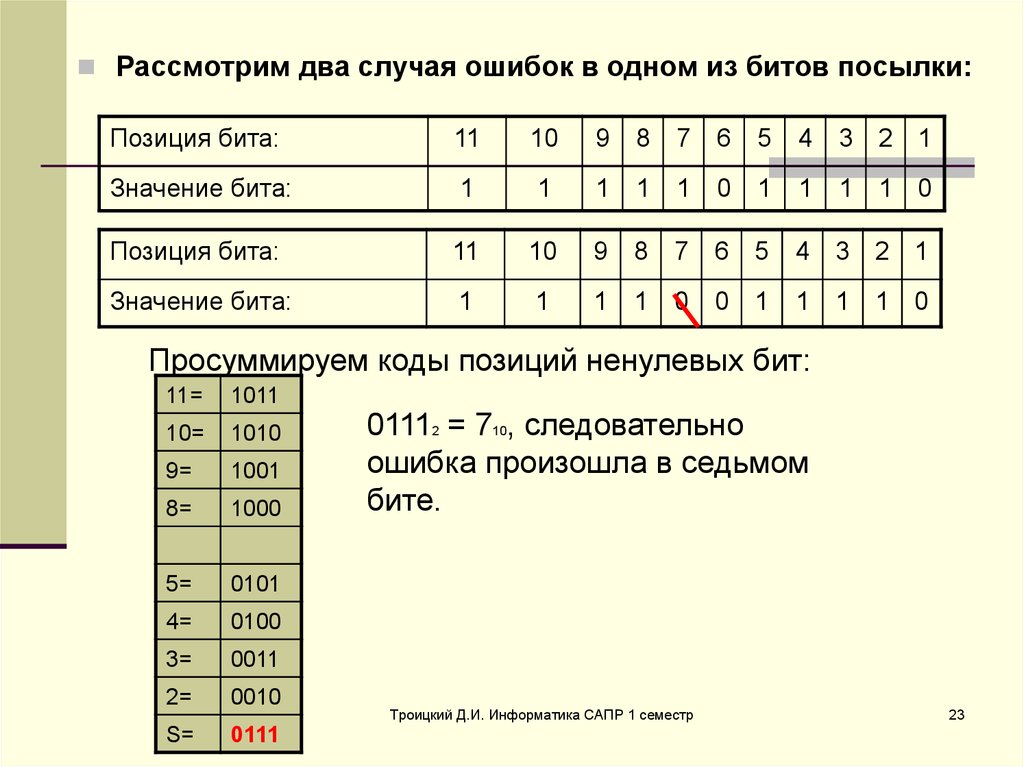
Рассмотрим два случая ошибок в одном из битов посылки:
Позиция бита:
11
10
9
8
7
6
5
4
3 2 1
Значение бита:
1
1
1
1
1
0
1
1
1 1 0
Позиция бита:
11
10
9
8
7
6
5
4
3 2 1
Значение бита:
1
1
1
1
0
0
1
1
1 1 0
Просуммируем коды позиций ненулевых бит:
11=
1011
10=
1010
9=
1001
8=
1000
5=
0101
4=
0100
3=
0011
2=
0010
S=
0111
01112 = 710, следовательно
ошибка произошла в седьмом
бите.
Троицкий Д.И. Информатика САПР 1 семестр
23

24.

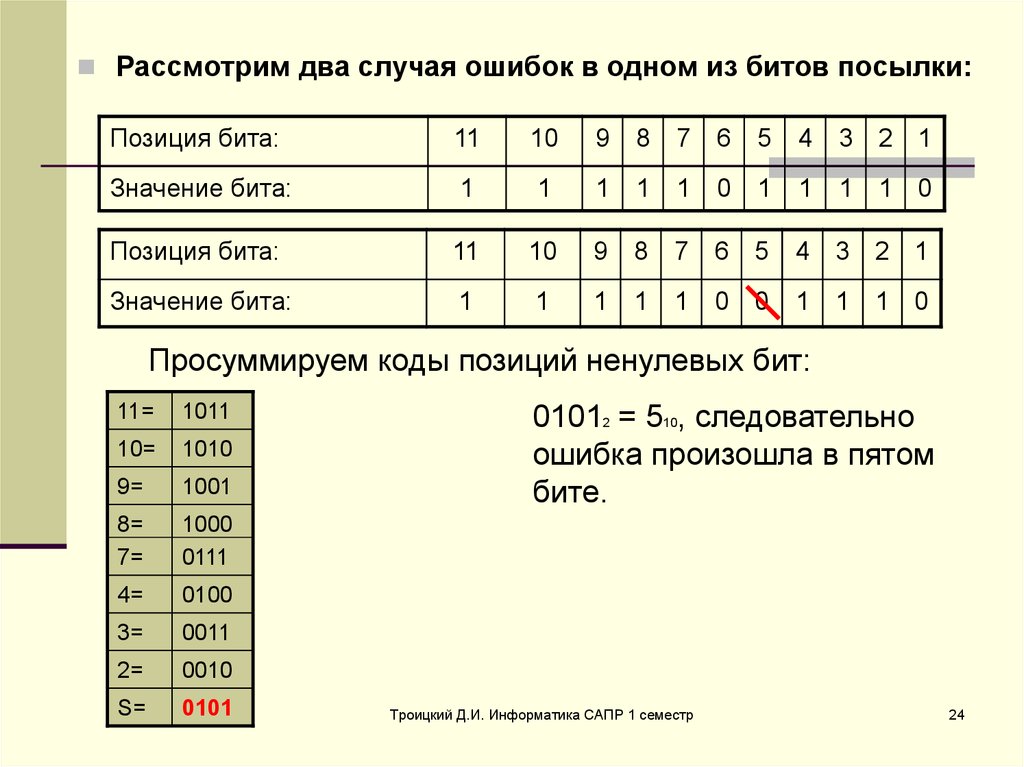
Рассмотрим два случая ошибок в одном из битов посылки:
Позиция бита:
11
10
9
8
7
6
5
4
3 2 1
Значение бита:
1
1
1
1
1
0
1
1
1 1 0
Позиция бита:
11
10
9
8
7
6
5
4
3 2 1
Значение бита:
1
1
1
1
1
0
0
1
1 1 0
Просуммируем коды позиций ненулевых бит:
11=
1011
10=
1010
9=
1001
8=
7=
1000
0111
4=
0100
3=
0011
2=
0010
S=
0101
01012 = 510, следовательно
ошибка произошла в пятом
бите.
Троицкий Д.И. Информатика САПР 1 семестр
24