Асинхронные потенциальные и синхронные автоматы

1.

ЛЕКЦИЯ № 2
Тема: Асинхронные потенциальные и
синхронные автоматы
Текст лекции по дисциплине «Цифровые устройства и микропроцессоры»
1

2.

УЧЕБНЫЕ ВОПРОСЫ:
1. Дискретные автоматы
2. Функциональные полные системы двоичных
функций
ЛИТЕРАТУРА:
Основная
Л1. А.К.Нарышкин «Цифровые устройств и микропроцессоры»: учеб. пособие
для студ. Высш. Учебн. Заведений/ А. К. Нарышкин, 2 – е изд. - Издательский
центр «Академия», 2008г. с. 52-76
Л2. Ю.Ф. Опадчий, О.П. Глудкин, А.И. Гуров «Аналоговая и цифровая
электроника», М.- Горячая линия- Телеком, 2000г. с. 509-513
Дополнительная
Л9. Б.А.Калабеков «Цифровые устройства и микропроцессорные систе-мы», М.:
«Горячая линия - телеком», 2000 г. с. 4-21, 204-206
2

3. 1. Дискретные автоматы

3

4. Основные понятия и определения

Обработка цифровой информации в ЭВМ производится
электронными схемами—цифровыми устройствами (ЦУ),
которые работают с двоичными кодами , получивишими название
цифровые автоматы
Автоматом называют любое устройство, осуществляющее
преобразование информации.
4

5. Классификация

1. В зависимости от типа сигналов, и характера работы автомата
во времени:
- автоматы непрерывного действия (используются непрерывные
по уровню сигналы);
- автоматы дискретного действия (дискретные автоматы)
(используются дискретные по уровню сигналы).
2. В зависимости от характера преобразования информации во
времени дискретные автоматы делятся на
синхронные;
асинхронные.
5

6. Классификация

В синхронном дискретном автомате возможны 2 способа
изменения значений уровня сигналов:
1). Изменения по уровню сигналов возможны лишь в отдельные
фиксированные моменты времени.
Время, выражаемое в номерах интервалов, называется
автоматным временем.
2). Сигналы могут принимать отличные от нуля значения лишь в
отдельные фиксированные моменты времени
Рис. 1 Изменение дискретного по уровню сигнала в функции автоматного
времени
В асинхронных дискретных автоматах моменты автоматного
времени не задаются принудительно с помощью генератора и
могут занимать любое положение во времени.
6

7.

Классификация
3. По зависимости сигналов на m выходах от сигналов на n
входах.
1). Значения сигналов на выходах автомата в данный момент
времени зависят только от значений сигналов на входах в тот же
момент времени:
yj(t) = Fj[xi(t)]; i=1,..., n; j=1,..., m.
Такой автомат называется автоматом без памяти или
комбинационной схемой, что тоже самое логическая схема.
2). Значения сигналов на выходах автомата в данный момент
времени зависят от значений сигналов на входах автомата в этот
же момент времени и предшествующие моменты времени:
yj(t)=Fj[xi(t), xi(t-1),..., xi(0)]; i=1,..., n, j=1,..., m.
Такой автомат называется автоматом с памятью
(последовательностные схемы)
7

8. Основные понятия и определения

Автоматы с кодированием значений сигналов цифрами (0 и 1)
часто называют цифровыми автоматами.
Для описания работы цифрового автомата используют
специальный математический аппарат - аппарат двоичных
функций.
Математический аппарат, в котором используются двоичные
функции двоичных аргументов, называется исчислением
высказываний или алгеброй логики или булевой алгеброй.
Математический аппарат, в котором используются двоичные
функции недвоичных аргументов, называется исчислением
предикатов.
8

9. 2. Функциональные полные системы двоичных функций

9

10. Основные понятия и определения

Алгебра логики оперирует следующими понятиями:
1). Переменная, которая может принимать два значения (0 и 1),
называется двоичной переменной.
2). Двоичная переменная, значение которой зависит от значений
других двоичных переменных аргументов, называется двоичной
функцией (булевой функцией, переключательной функцией или
функцией алгебры логики).
Число, двоичный код которого образуется набором значений
аргументов, называется номером набора. (Набор это конкретная
комбинация, в которой логические переменные принимают
конкретные значения).
n
Всего от n аргументов может быть задано N = 2 2 различных
двоичных функций.
Процесс определения значения двоичной функции по значениям ее
аргументов называется логической операцией.
10

11. Двоичные функции одного аргумента

Известно, что от одного двоичного аргумента x может быть
образовано четыре разных двоичных функций yj = Fj(x). Значения
этих функций приведены в табл. 1.
Таблица 1
11

12. Двоичные функции одного аргумента

Функция y0 сохраняет нулевое значение. Это константа нуля
(y0=0). Функция y3 - сохраняет единичное значение при любом
значении аргумента. Это константа единицы (y3=1).
Функция y1 принимает значение, равное значению ее аргумента.
Такая функция y1=x называется тавтологией. Ее реализует
логический элемент повторитель,
Функция y2 принимает значение, противоположное значению ее
аргумента. Такая функция называется инверсией. Выполняет
операцию отрицания (НЕ). Для обозначения операции отрицания
используется запись следующего вида: y = x . Функция инверсия
реализуется логическим элементом - инвертором
12

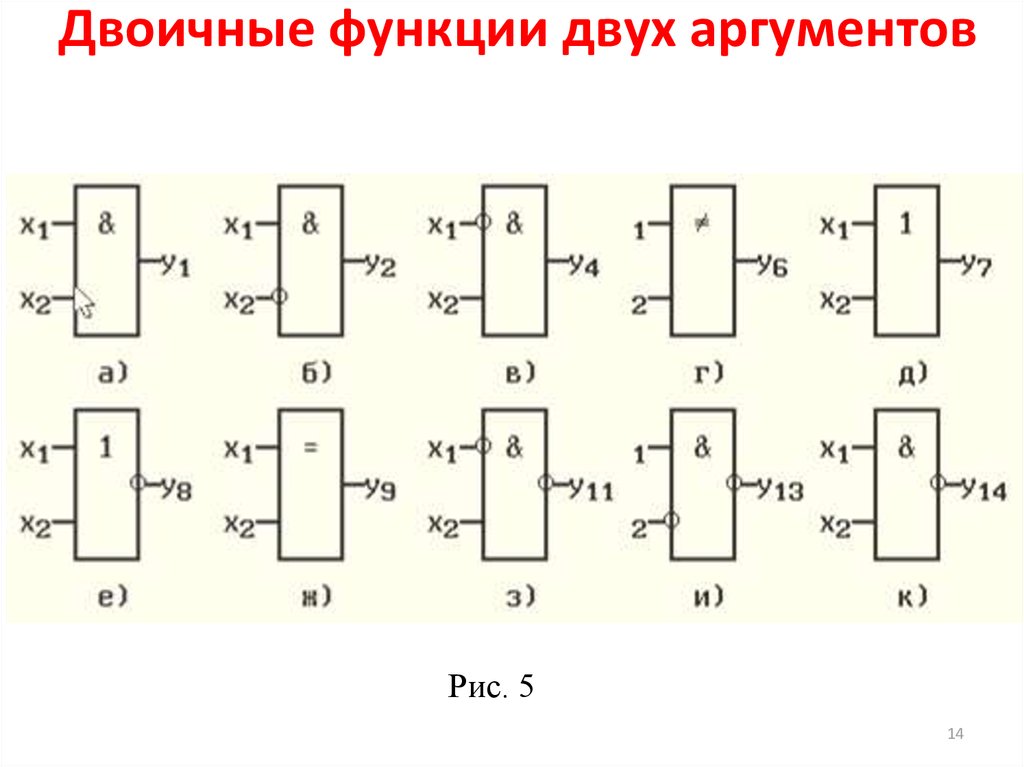
13. Двоичные функции двух аргументов

От двух двоичных аргументов x1 и x2 могут быть образованы
шестнадцать разных двоичных функций yj=Fj(x1,x2), значения
которых приведены в табл. 2.
Таблица 2
n=2
13

14. Двоичные функции двух аргументов

Рис. 5
14

15. Функциональные полные системы двоичных функций

Подставляя в качестве аргументов одних двоичных функций другие
двоичные функции, можно получить новые двоичные функции
(операция суперпозиции. )
Например, при подстановке в двоичную функцию z=F(y1,y2)
двоичных функций y1=F(x1,x2) и y2=F(x3,x4) получается двоичная
функция четырех аргументов z=F(x1,x2,x3,x4).
Совокупность двоичных функций, с использованием которых в
результате выполнения операций суперпозиции может быть
получена сколь угодно сложная двоичная функция любого
конечного числа двоичных аргументов, называется функционально
полной системой (ФПС) двоичных функций.
15

16. Функциональные полные системы двоичных функций

Функционально полная система функций, состоящая из трех
функций - дизъюнкции, конъюнкции и инверсии, называется
основной функционально полной системой (ОФПС) двоичных
функций
Набор простейших логических функций, позволяющих реализовать
любую другую функцию называется логическим базисом (ЛБ).
Функции И, ИЛИ, НЕ не являются минимальным ЛБ, т.к. сами
могут быть представлены через другие функции, например через
ИЛИ -НЕ или И - НЕ.
Следовательно базис "И - НЕ" или "ИЛИ - НЕ" является
минимальным логическим базисом.
16

17.

1.
2.
3.
4.
5.
ЗАКЛЮЧЕНИЕ:
Автоматом называют любое устройство, осуществляющее
преобразование информации.
Переменная, которая может принимать два значения (0 и 1),
называется двоичной переменной.
Двоичная переменная, значение которой зависит от значений
других двоичных переменных аргументов, называется
двоичной функцией (булевой функцией, переключательной
функцией или функцией алгебры логики).
Процесс определения значения двоичной функции по
значениям ее аргументов называется логической операцией.
Совокупность двоичных функций, с использованием которых в
результате выполнения операций суперпозиции может быть
получена сколь угодно сложная двоичная функция любого
конечного числа двоичных аргументов, получила название
функционально полной системы (ФПС) двоичных
функций.
17