Similar presentations:
Алгоритм Дейкстры. (Лекция 5)
1.
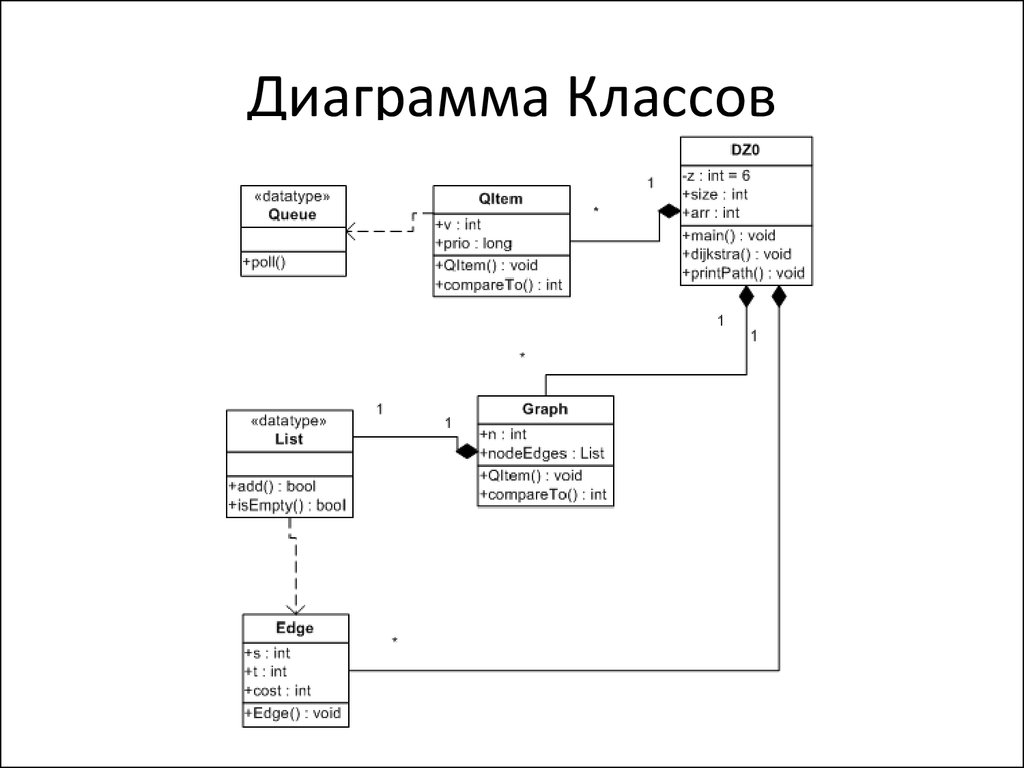
Алгоритм Дейкстры2. Диаграмма Классов
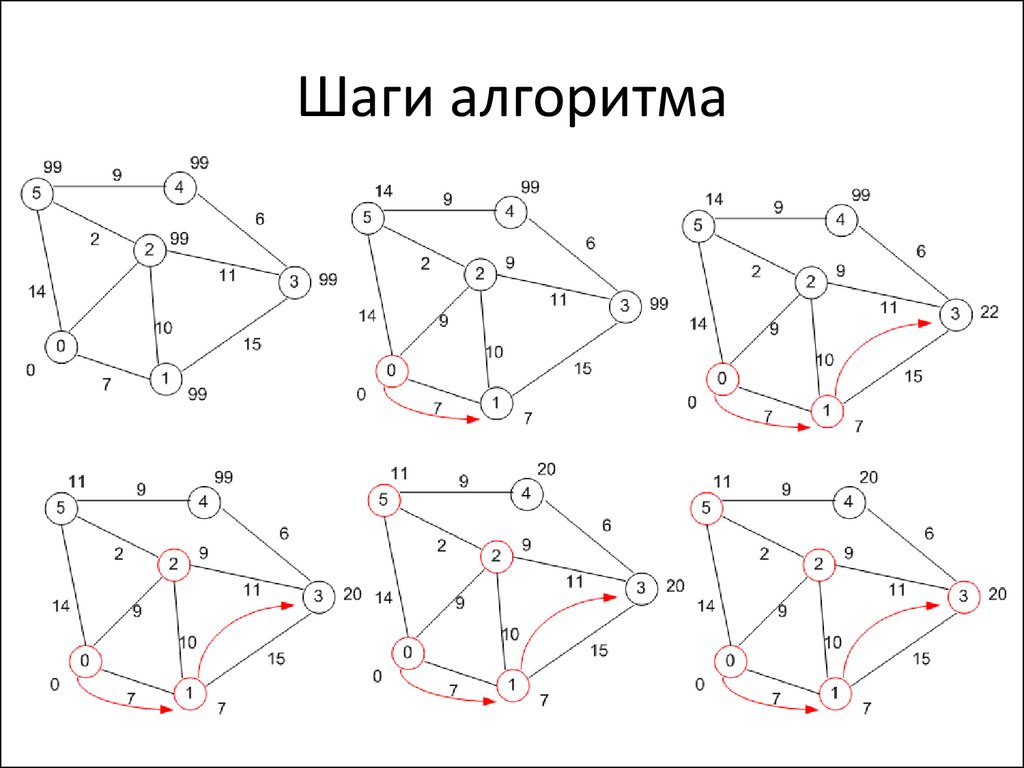
3. Шаги алгоритма
4.
static final int arr[][] = new int[][] {{0, 7, 9, 99, 99, 14},
{7, 0, 10, 15, 99, 99},
{9, 10, 0, 11, 99, 2},
{99, 15, 11, 0, 6, 99},
{99, 99, 99, 6, 0, 9},
{14, 99, 2, 99, 9, 0}
};
5.
public static final long INF = Long.MAX_VALUE / 10;Реализация Классов
public static class QItem implements Comparable<QItem> {
long prio; int v;
public QItem(long prio, int v) { this.prio = prio; this.v = v; }
public int compareTo(QItem q) { return prio < q.prio ? -1 : prio > q.prio ? 1 : 0; } },
В интерфейсе Comparable объявлен всего один метод compareTo(Object obj), предназначенный для
реализации упорядочивания объектов класса. Его удобно использовать при сортировке упорядоченных
списков
или
массивов
объектов.
Данный
метод
сравнивает
вызываемый
объект
с obj. compareTo возвращает:·
0, если значения равны;
Отрицательное значение, если
вызываемый объект меньше параметра;
Положительное значение , если вызываемый объект больше
параметра.
public static class Edge {
public int s, t, cost;
public Edge(int s, int t, int cost) { this.s = s; this.t = t; this.cost = cost; } }
nodeEdges
public static class Graph {
0
1
2
3
4
5
public final int n;
Edge
arrayList
public List<Edge>[] nodeEdges;
public Graph(int n) {
this.n = n;
nodeEdges = new List[n];
for (int i = 0; i < n; i++) { nodeEdges[i] = new ArrayList<Edge>(); } }
void addEdge(int s, int t, int cost) {
nodeEdges[s].add(new Edge(s, t, cost)); } }
6.
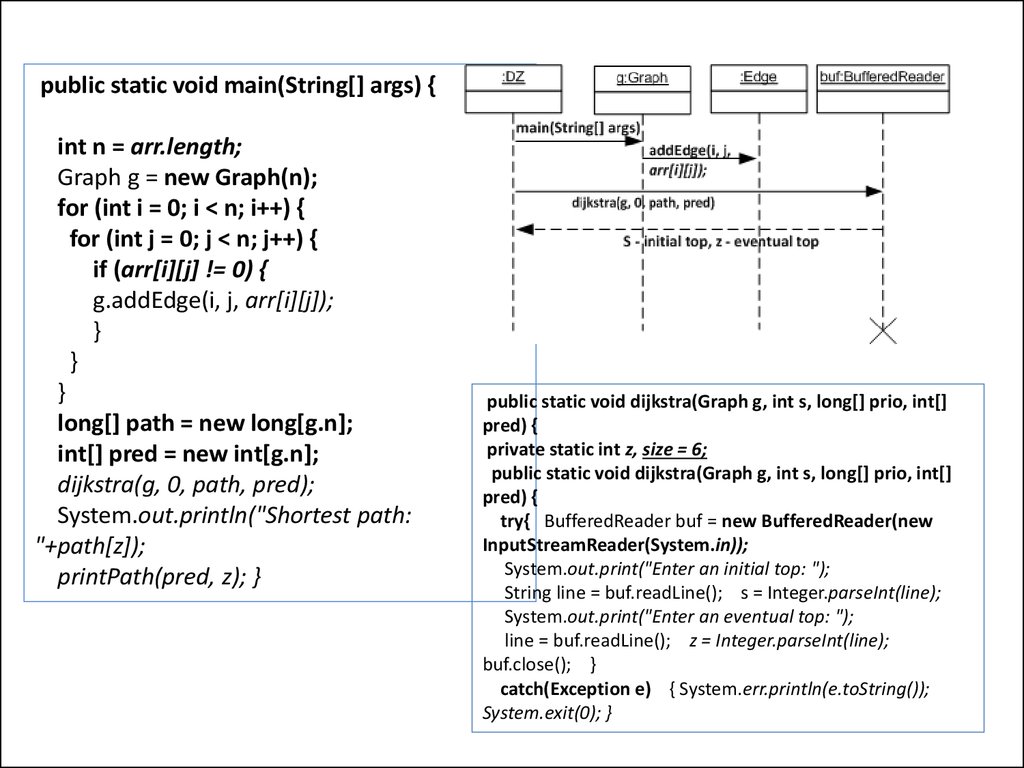
public static void main(String[] args) {int n = arr.length;
Graph g = new Graph(n);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (arr[i][j] != 0) {
g.addEdge(i, j, arr[i][j]);
}
}
}
long[] path = new long[g.n];
int[] pred = new int[g.n];
dijkstra(g, 0, path, pred);
System.out.println("Shortest path:
"+path[z]);
printPath(pred, z); }
public static void dijkstra(Graph g, int s, long[] prio, int[]
pred) {
private static int z, size = 6;
public static void dijkstra(Graph g, int s, long[] prio, int[]
pred) {
try{ BufferedReader buf = new BufferedReader(new
InputStreamReader(System.in));
System.out.print("Enter an initial top: ");
String line = buf.readLine(); s = Integer.parseInt(line);
System.out.print("Enter an eventual top: ");
line = buf.readLine(); z = Integer.parseInt(line);
buf.close(); }
catch(Exception e) { System.err.println(e.toString());
System.exit(0); }
7.
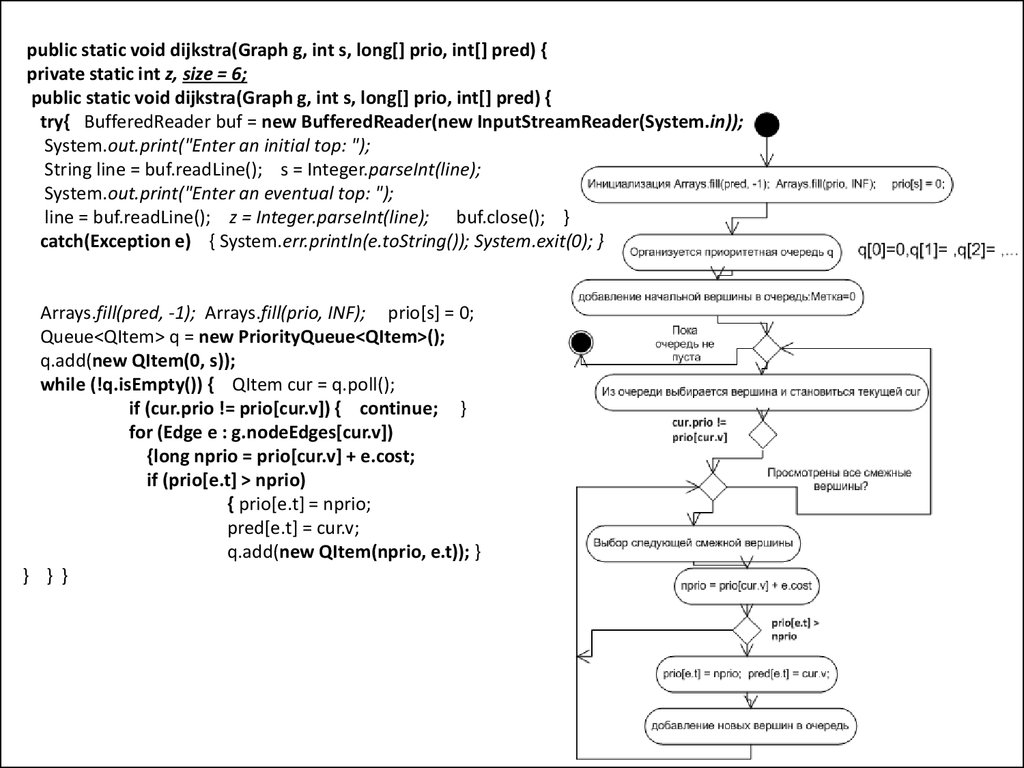
public static void dijkstra(Graph g, int s, long[] prio, int[] pred) {private static int z, size = 6;
public static void dijkstra(Graph g, int s, long[] prio, int[] pred) {
try{ BufferedReader buf = new BufferedReader(new InputStreamReader(System.in));
System.out.print("Enter an initial top: ");
String line = buf.readLine(); s = Integer.parseInt(line);
System.out.print("Enter an eventual top: ");
line = buf.readLine(); z = Integer.parseInt(line); buf.close(); }
catch(Exception e) { System.err.println(e.toString()); System.exit(0); }
Arrays.fill(pred, -1); Arrays.fill(prio, INF); prio[s] = 0;
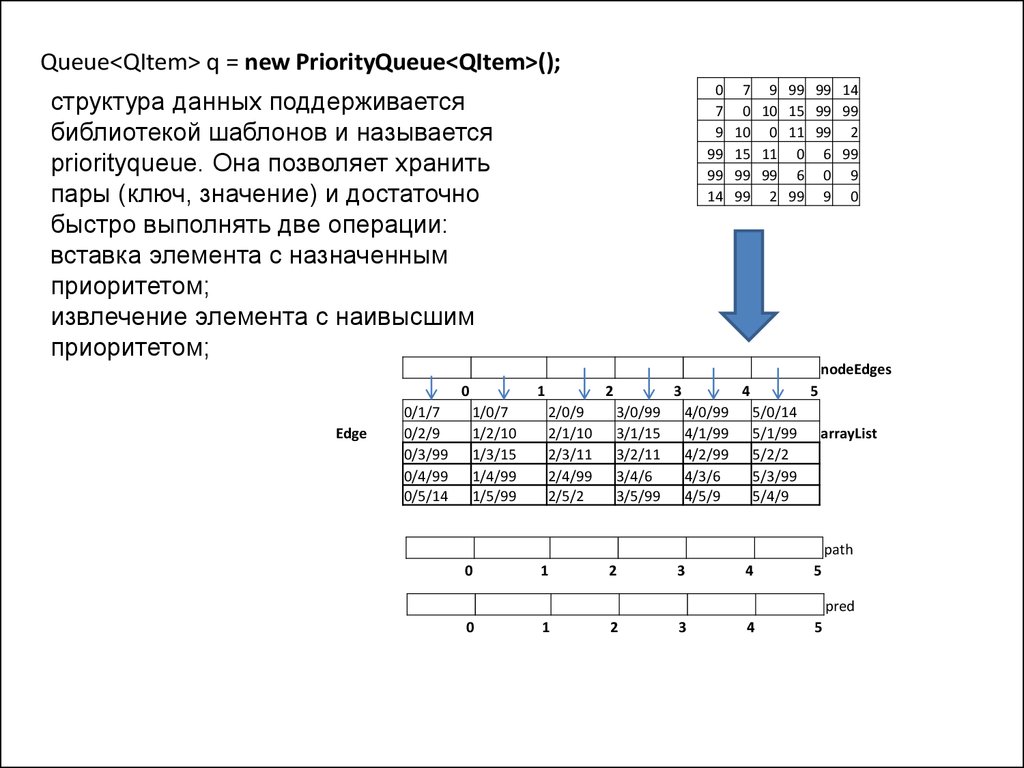
Queue<QItem> q = new PriorityQueue<QItem>();
q.add(new QItem(0, s));
while (!q.isEmpty()) { QItem cur = q.poll();
if (cur.prio != prio[cur.v]) { continue; }
for (Edge e : g.nodeEdges[cur.v])
{long nprio = prio[cur.v] + e.cost;
if (prio[e.t] > nprio)
{ prio[e.t] = nprio;
pred[e.t] = cur.v;
q.add(new QItem(nprio, e.t)); }
} } }
8.
Queue<QItem> q = new PriorityQueue<QItem>();0
7
9
99
99
14
структура данных поддерживается
библиотекой шаблонов и называется
priorityqueue. Она позволяет хранить
пары (ключ, значение) и достаточно
быстро выполнять две операции:
вставка элемента с назначенным
приоритетом;
извлечение элемента с наивысшим
приоритетом;
7 9 99 99 14
0 10 15 99 99
10 0 11 99 2
15 11 0 6 99
99 99 6 0 9
99 2 99 9 0
nodeEdges
0
Edge
0/1/7
0/2/9
0/3/99
0/4/99
0/5/14
1
1/0/7
1/2/10
1/3/15
1/4/99
1/5/99
2
2/0/9
2/1/10
2/3/11
2/4/99
2/5/2
3
3/0/99
3/1/15
3/2/11
3/4/6
3/5/99
4
4/0/99
4/1/99
4/2/99
4/3/6
4/5/9
5
5/0/14
5/1/99
5/2/2
5/3/99
5/4/9
arrayList
path
0
1
2
3
4
5
pred
0
1
2
3
4
5



 programming
programming








