Статистические показатели

1. Статистические показатели

• Абсолютные и относительные
• Средние и вариация
• Экономические индексы

2. Статистический показатель

R
Статистический показатель
- количественно-качественная
обобщающая характеристика
какого-либо свойства
группы единиц или
совокупности в целом

3. Типы показателей

R
Типы показателей
• Первичные (объемные, экстенсивные)
• Вторичные (производные, интенсивные)
• Индивидуальные
• Сводные
(единичные)
(групповые, суммарные)

4. Абсолютные показатели

• характеризуют абсолютные
размеры явлений (масса, площадь,
объем, количество)
• Имеют размерность (ед.изм.)
– натуральные (куб.м., КВт ч, тонна, км,…)
– условно-натуральные (усл.топливо,
эталонный трактор,…)
– стоимостные (денежные, сопоставимые)
– трудовые (чел-день, чел-час)
затраты труда, трудоемкость

5. Относительные показатели

6. Относительные показатели

- результат деления
двух абсолютных показателей =
текущий (сравниваемый)
база сравнения
Цели:
• сравнение двух абсолютных
• сравнение нескольких абсолютных
с одним базовым
• «цепное» сравнение ряда показателей

7. Относительные показатели

- сравнение двух одноименных
абсолютных показателей =
текущий (сравниваемый) * масштаб
база сравнения
Виды:
Масштаб базы: Размерность:
– коэффициент (1)
– процент
(100 %)
– промилле
(1000 %о)
– продецимилле (10000 %оо)
раз
%
%о
«на 10000…»

8. Относительные показатели

- сравнение двух разноименных
абсолютных показателей =
текущий (сравниваемый)
база сравнения
Сочетание наименований
– Затраты на хранение товара
[% от цены / год]

9. Относительные показатели

Виды относительных показателей
• Динамики (ОПД)
• Плана (ОПП)
• Выполнения плана (ОПВП)
• Структуры (ОПСт)
• Координации (ОПК)
• Интенсивности и уровня развития
• Сравнения (ОПСр)

10. ОП динамики

Для ряда динамики X1 … XN
ОПД = (тек.ур.) / (предыд.или баз.ур.)
• постоянная база (базисные ОПД)
– сравнение с началом периода
ОПД( i ) = Xi / X1 , i = 1..N, ОПД(1) = 1
• переменная база (цепные ОПД)
– сравнение с предыдущим периодом
(темп роста)
ОПД( i ) = Xi / Xi-1 , i = 2..N

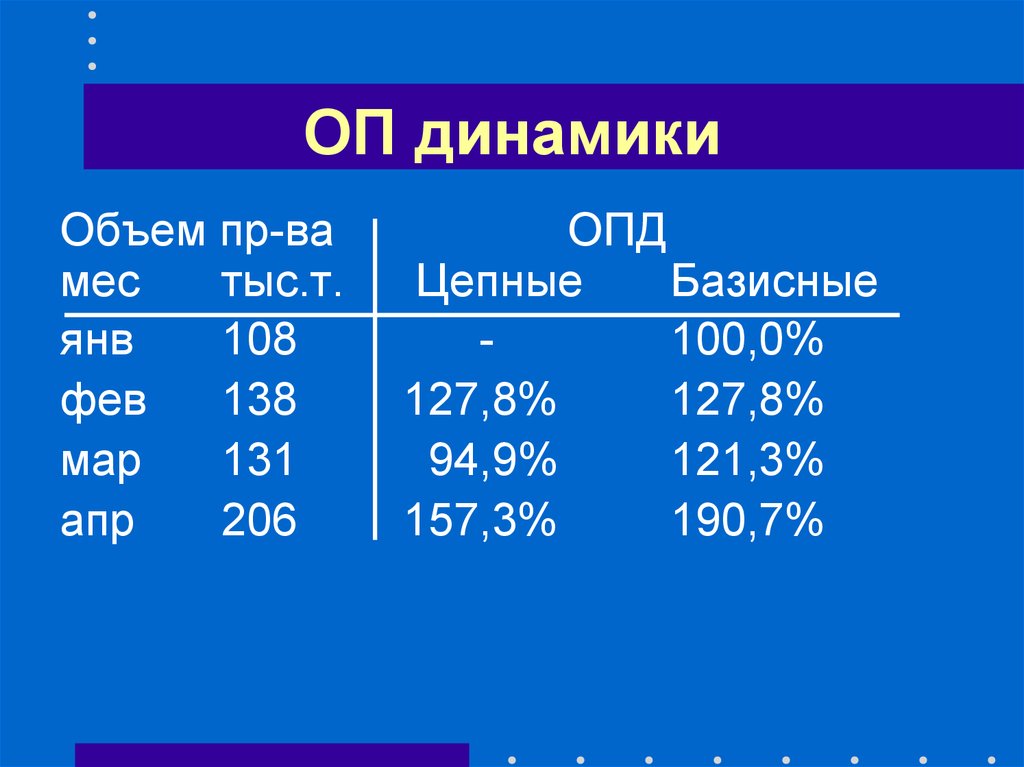
11. ОП динамики

Объем пр-ва
мес
тыс.т.
янв
108
фев
138
мар
131
апр
206
ОПД
Цепные
Базисные
100,0%
127,8%
127,8%
94,9%
121,3%
157,3%
190,7%

12. ОП плана и его выполнения

Для ряда плана
Y1 … YN
ОППY( i ) = Yi+1 / Yi
(предстоит на следующий период)
Для ряда выполнения плана X1 … XN
ОПВПXY( i ) = Xi / Yi

13. ОП структуры и координации

Для набора показателей Y1 … YN
Структура:
ОПC( i ) = Yi / ( Yi )
Координация:
ОПК( i ) = Yi / Y1
Y1 - база сравнения:
- max(Yi )
- наибольший интерес

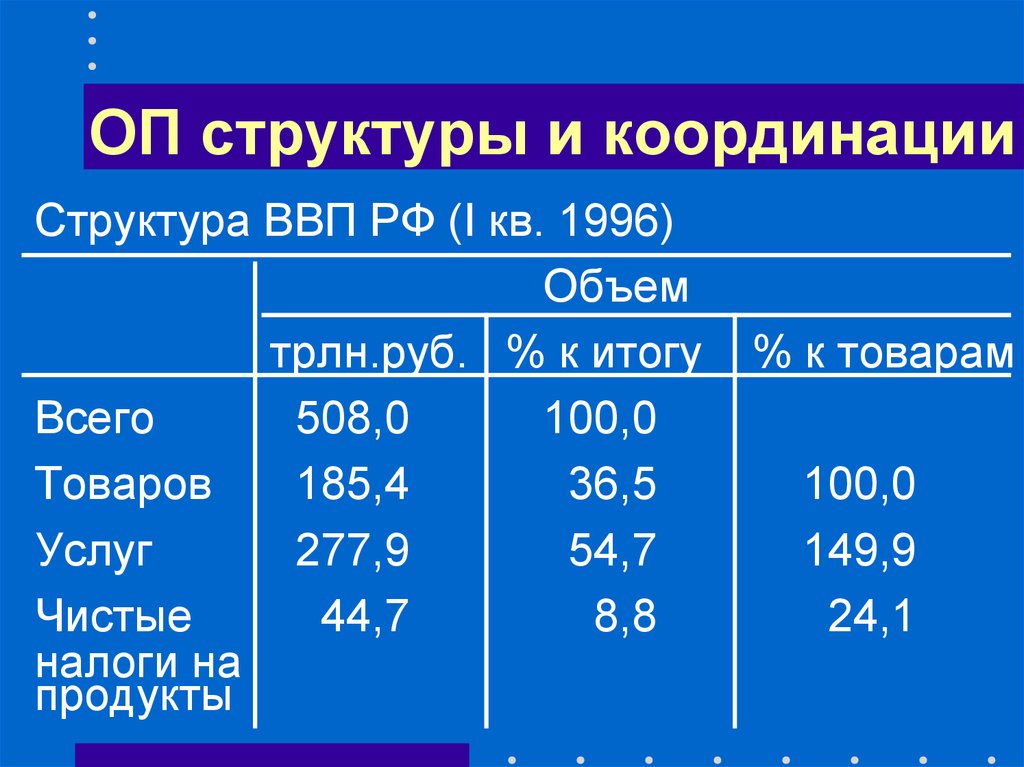
14. ОП структуры и координации

Структура ВВП РФ (I кв. 1996)
Объем
трлн.руб. % к итогу
Всего
508,0
100,0
Товаров
185,4
36,5
Услуг
277,9
54,7
Чистые
44,7
8,8
налоги на
продукты
% к товарам
100,0
149,9
24,1

15. ОП интенсивности

ОПИ = (характеристика явления А)
(распространенность А)
характеризует распространенность
явления (%, промилле, продецимилле)
– Уровень обеспеченности автомобилями
[число машин на 100 семей]
– Плотность населения
[число людей, приходящееся на 1 кв.км.]
– Уровень предложения на рынке труда
[число безработных на 1 вакансию]

16. ОП сравнения

• Отношение одноименных
абсолютных показателей,
характеризующих разные объекты
ОПCр = (характеристика объекта А)
(характеристика объекта B)
– В Москве дилеров в 12,1 раза больше,
чем в Новосибирске
– Объем продаж обуви в 7 раз больше
продаж одежды

17. Средние величины

18. Средняя величина

- обобщенный показатель,
характеризующий типический
уровень признака (средняя по типу)
Сравнение зарплат на 2-х предприятиях:
• по зарплатам 2-х работников (индив.)
• по фонду оплаты труда
(объемн.)
• по средней зарплате
(средн.)

19. Принципы применения

• Для погашения индив. различий
• Расчет по однородной совокупности
• Подкрепление общих средних
групповыми средними
• Учет качественного содержания,
взаимосвязи с другими признаками,
имеющимися данными

20. Виды средних величин

• Структурные
• Степенные
n
m
1
m
Xi
n i 1
– Гармоническая m = -1
– Геометрическая m 0
n
– Арифметическая m = 1
– Квадратичная
m=2 n
i
– Кубическая
m=3
i 1
Мажорируемость:
Xгарм Xгеом Xар Xкв Xкуб
X

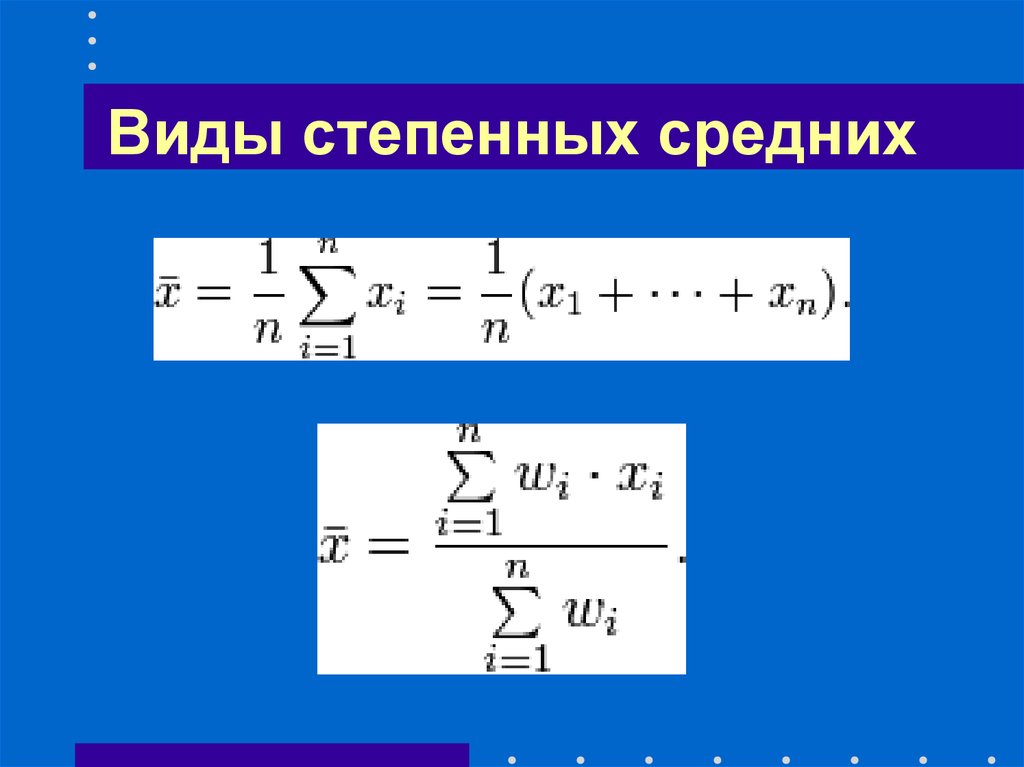
21. Виды степенных средних

Простые
Взвешенные
n
m
1
m
Xi
n i 1
n
n
X
i
i 1
n
m
fX
i
i 1
n
fi
m
i
X
i
i 1
fi
n
f
i 1
i

22. Виды степенных средних

23. Виды степенных средних

Пример. Имеются данные о заработной плате десяти работников предприятия:
Вычислить среднюю месячную зарплату рабочих:
Профессия
Количество рабочих
Заработная плата (руб.)
Токари
5
1700, 1208, 1620, 917, 1400
Фрезеровщики
2
1810, 1550
Слесари
3
1210, 1380, 870
n
х
х
i 1
n
i
1700 1208 917 1620 1400 1810 1550 1210 1380 870
1365,5 руб.
10

24. Виды степенных средних

Пример. Имеются данные о стаже рабочих на предприятии:
Определить средний стаж рабочих.
Стаж работы
(хi)
Количество
рабочих (fi)
До 5 лет
5-10 лет
2
6
10-15
лет
15
15 лет и
более
7
Итого
30
4
х
х f
i
i 1
4
f
i 1
i
i
2,5 2 7,5 6 12,5 15 17,5 7 360
12 лет.
2 6 15 7
30

25. Пример 1 (выбор типа средней)

Какова средняя урожайность?
Культура Вал.сбор
Посев.
(ц)
площ. (га)
Пшеница 32 500
1 540 У = ВСi
ППi
Рожь
1 620
120
Ячмень
13 640
460
Просо
1 650
80
Итого
49 410
2 200

26. Пример 2 (выбор типа средней)

Какова средняя урожайность?
Культура Посев.
Урожайность
площ. (га) (ц/га)
Пшеница 1 540
20
У = Уi ППi
ППi
Рожь
120
19
Ячмень
460
28
Просо
80
13
Итого
2 200
?

27. Пример 3 (выбор типа средней)

Какова средняя урожайность?
Культура Вал.сбор
Урожайность
(ц)
(ц/га)
Пшеница 32 500
25
У = ВСi__
ВСi/Уi
Рожь
1 620
18
Ячмень
13 640
22
Просо
1 650
15
Итого
49 410
?

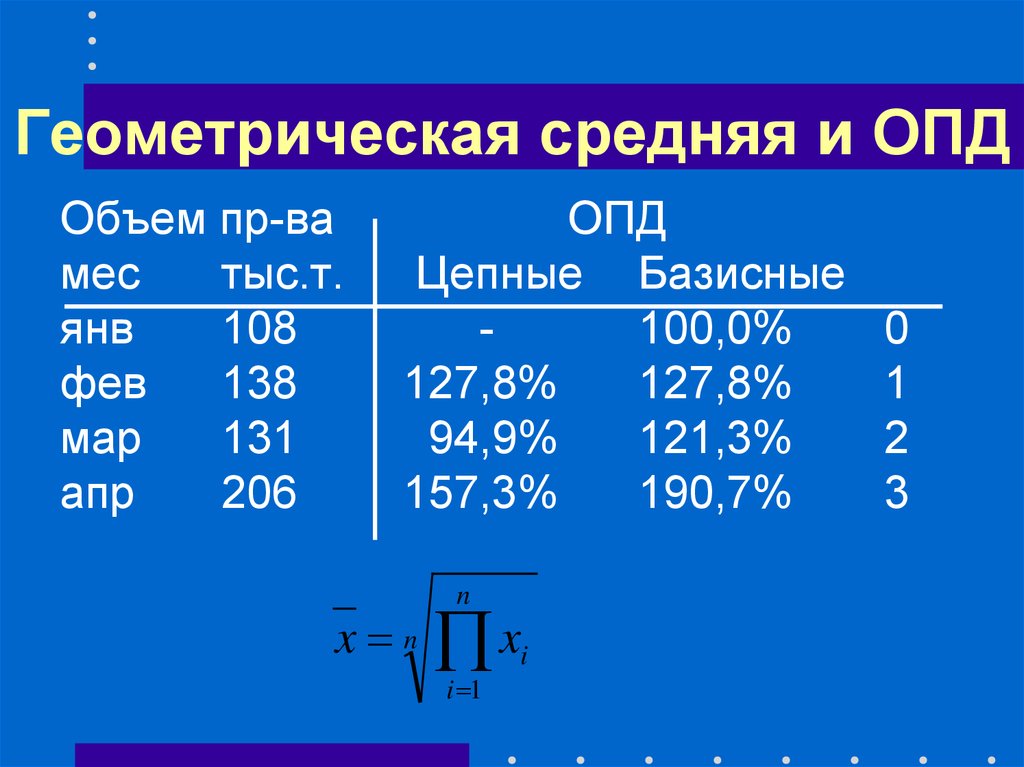
28. Геометрическая средняя и ОПД

Объем пр-ва
мес
тыс.т.
янв
108
фев
138
мар
131
апр
206
ОПД
Цепные Базисные
100,0%
127,8%
127,8%
94,9%
121,3%
157,3%
190,7%
x n
n
x
i
i 1
0
1
2
3

29. Структурные средние

• Мода (наиболее частое значение)
• Медиана (серединный объем)
Причины применения
• Выявление внутреннего строения
ряда распределения признака
• При невозможности определения
среднего в интервальном ряде
распределения

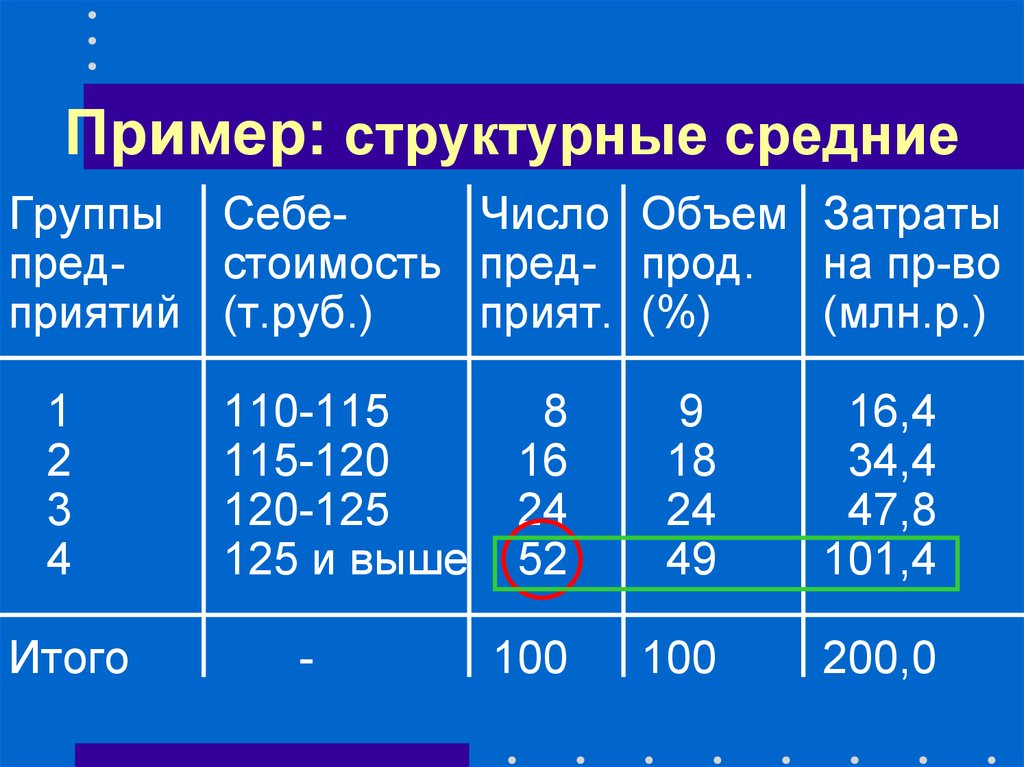
30. Пример: структурные средние

Группы СебеЧисло Объем Затраты
предстоимость пред- прод. на пр-во
приятий (т.руб.)
прият. (%)
(млн.р.)
1
2
3
4
Итого
110-115
115-120
120-125
125 и выше
-
8
16
24
52
9
18
24
49
16,4
34,4
47,8
101,4
100
100
200,0

31. Расчет моды

Мо = ХМо + hМо
[fMo-fMo-1] / [(fMo-fMo-1)+(fMo-fMo+1)]
ХМо
hМo
fМо
f Мо-1
f Мо+1
- нижняя гр. модального инт.
- ширина модального инт.
- объем в медианном интервале
- объем в предыдущем инт.
- объем в следующем инт.

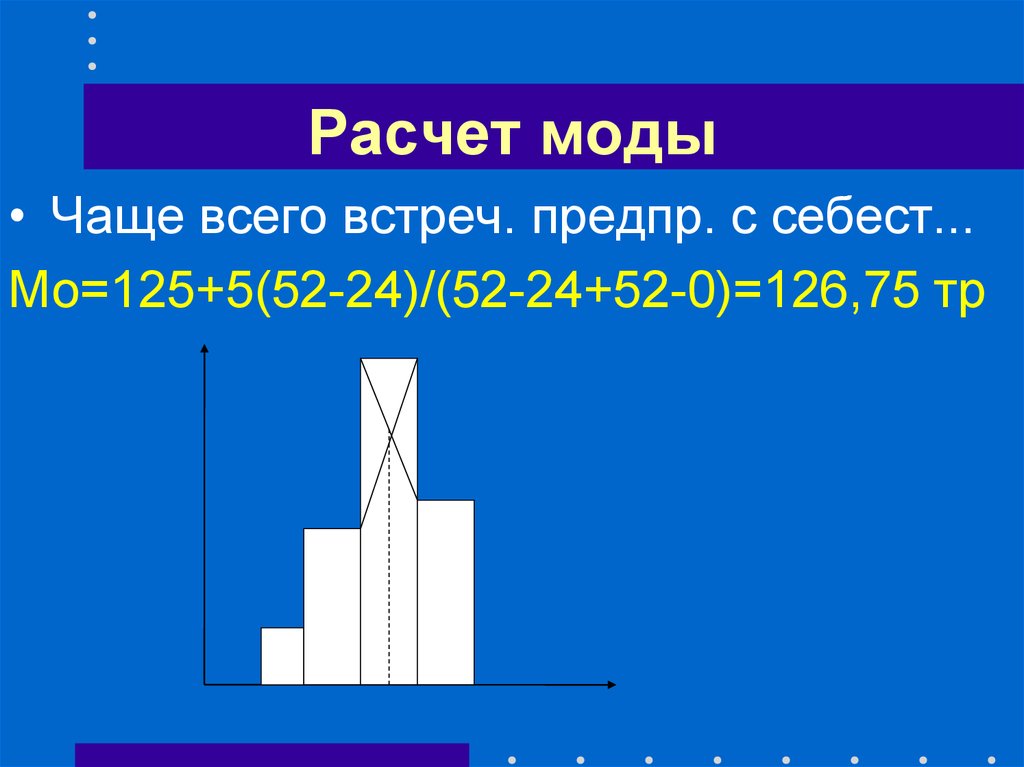
32. Расчет моды

• Чаще всего встреч. предпр. с себест...
Мо=125+5(52-24)/(52-24+52-0)=126,75 тр

33. Расчет медианы

Ме = ХМе + hМе [(n/2)-SМе-1]/ fМе
ХМе
hМе
n/2
SМе-1
fМе
- нижняя гр. медианного инт.
- ширина медианного инт.
- половина объема взвеш. показ.
- накопленный до мед.инт. объем
- объем в медианном интервале

34. Расчет медианы

• 1/2 объема пр-ва с ур. себест. выше...
Ме =120+5(50-27)/24=124,79 т.руб.

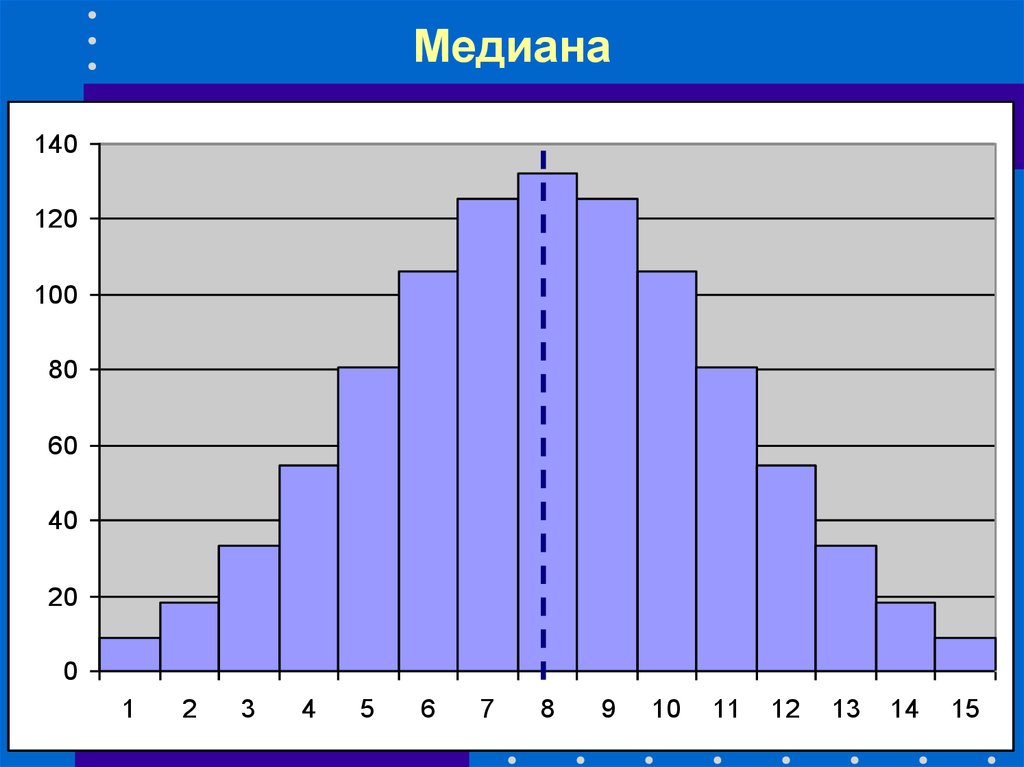
35. Медиана

140
120
100
80
60
40
20
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

36. Медиана

0,14
0,12
0,1
0,08
0,06
0,04
0,02
0
1 2 3 4
5 6 7
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Xme

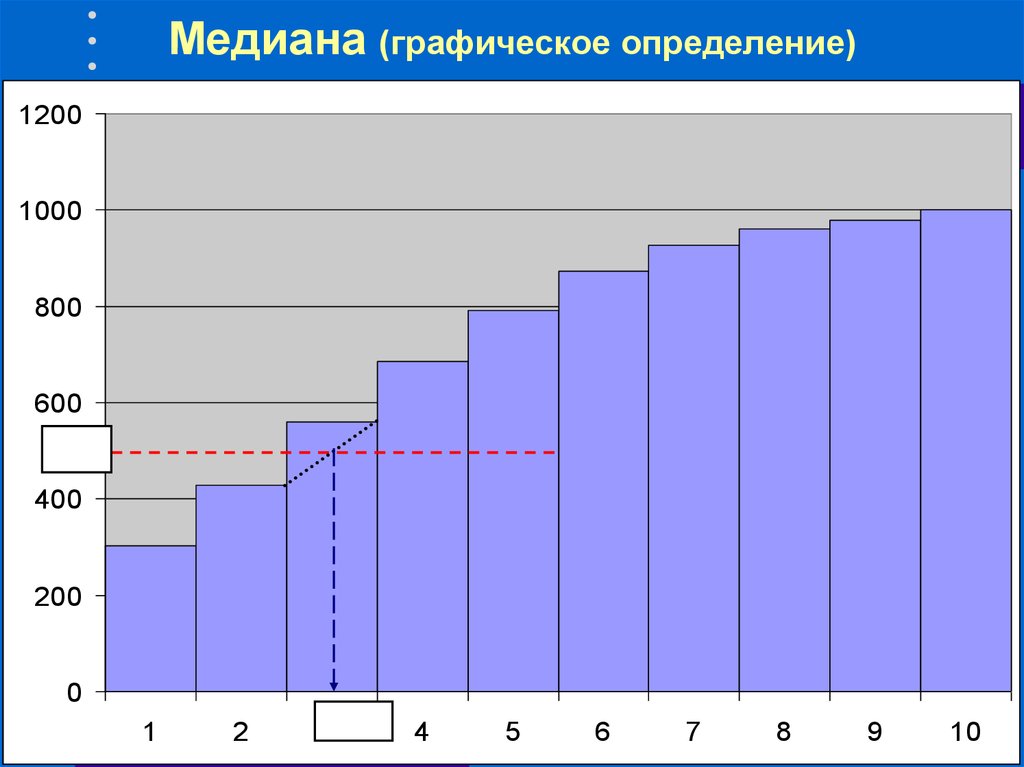
37. Медиана (графическое определение)

1200
1000
800
600
n/2
400
200
0
1
2
3XMe
4
5
6
7
8
9
10

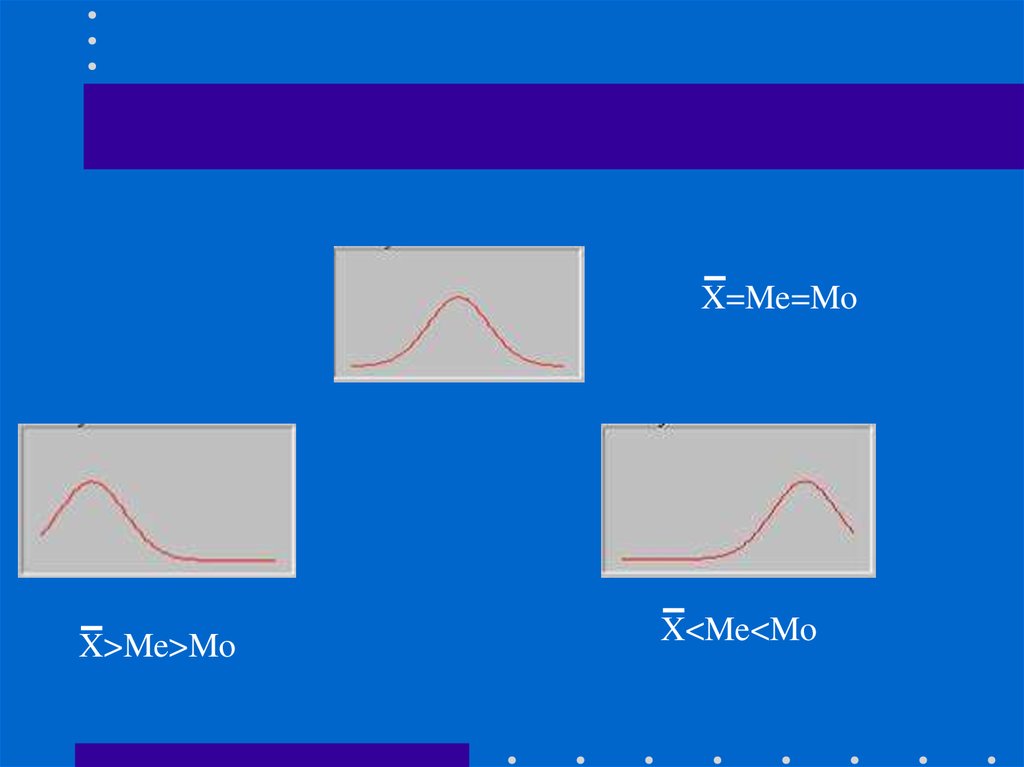
38.

X=Me=Mo
X>Me>Mo
X<Me<Mo

39. Симметричный ряд

0,14
0,12
0,1
0,08
0,06
0,04
0,02
0
1
3
5
7
9
11
13
15
17
19
21
23

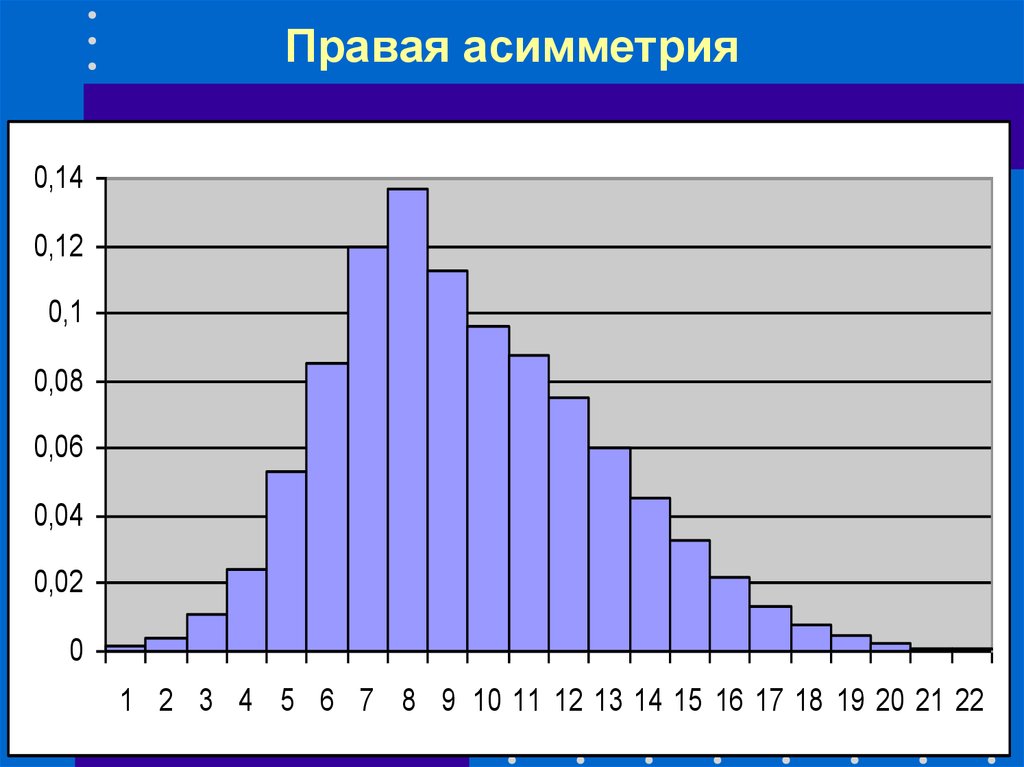
40. Правая асимметрия

0,14
0,12
0,1
0,08
0,06
0,04
0,02
0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

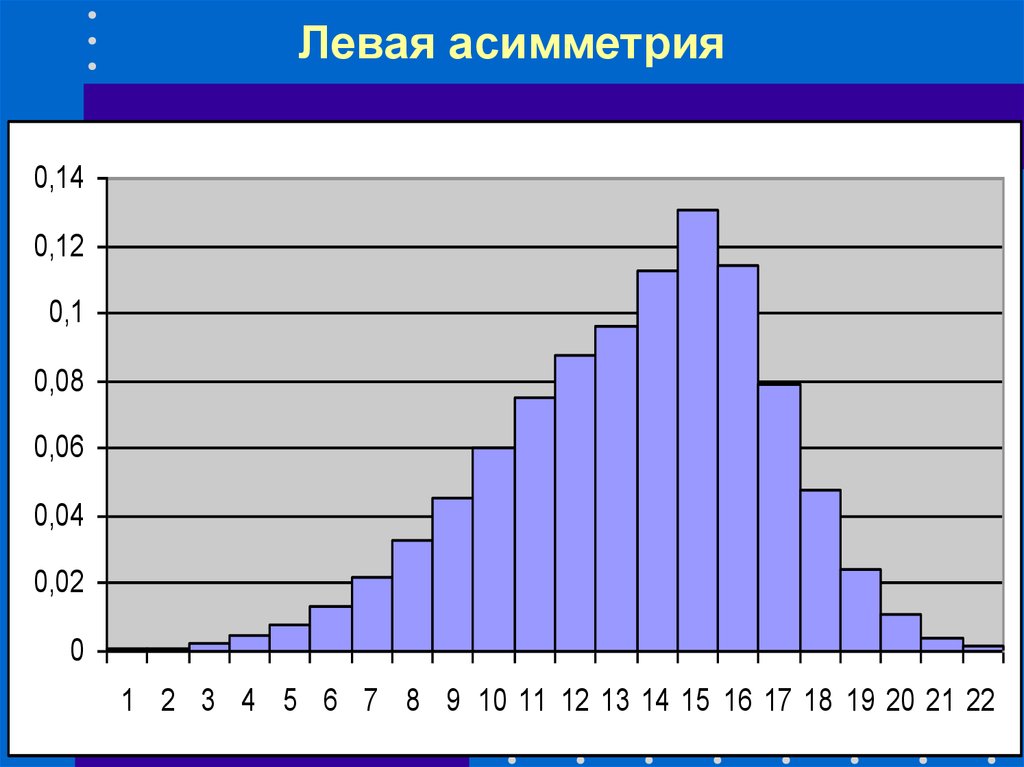
41. Левая асимметрия

0,14
0,12
0,1
0,08
0,06
0,04
0,02
0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

42. Показатели вариации

43. Вариация

- различие в значениях показателя у
разных единиц совокупности в один и
тот же период или момент времени
Показатель вариации характеризует:
• Структуру явления (степень
отклонения варианты от средней)
• Точность определения
средней величины

44. Показатели вариации

Размах вариации
Среднее линейное отклонение
Дисперсия
Среднее квадратическое отклонение
Коэффициент вариации

45. Размах вариации

R = Xmax - Xmin
• Характеристика возможных
резервов (в предположении, что
часть единиц может достичь
наилучшего показателя)

46. Среднее линейное отклонение

• Для несгруппированных данных
d = (1/N) i=1..N | Xi - X |
• Для вариационного ряда (сгруппир.)
d = i=1..m | Xi - X | fi / i=1..m fi

47. Дисперсия

• Простая дисперсия
для несгруппированных данных
2 = (1/N) i=1..N | Xi - X |2
• Взвешенная дисперсия
для вариационного ряда
2 = i=1..m | Xi - X |2 fi / i=1..m fi

48. Дисперсия

• Вычисление через моменты
2
=
2
_
X
X
2

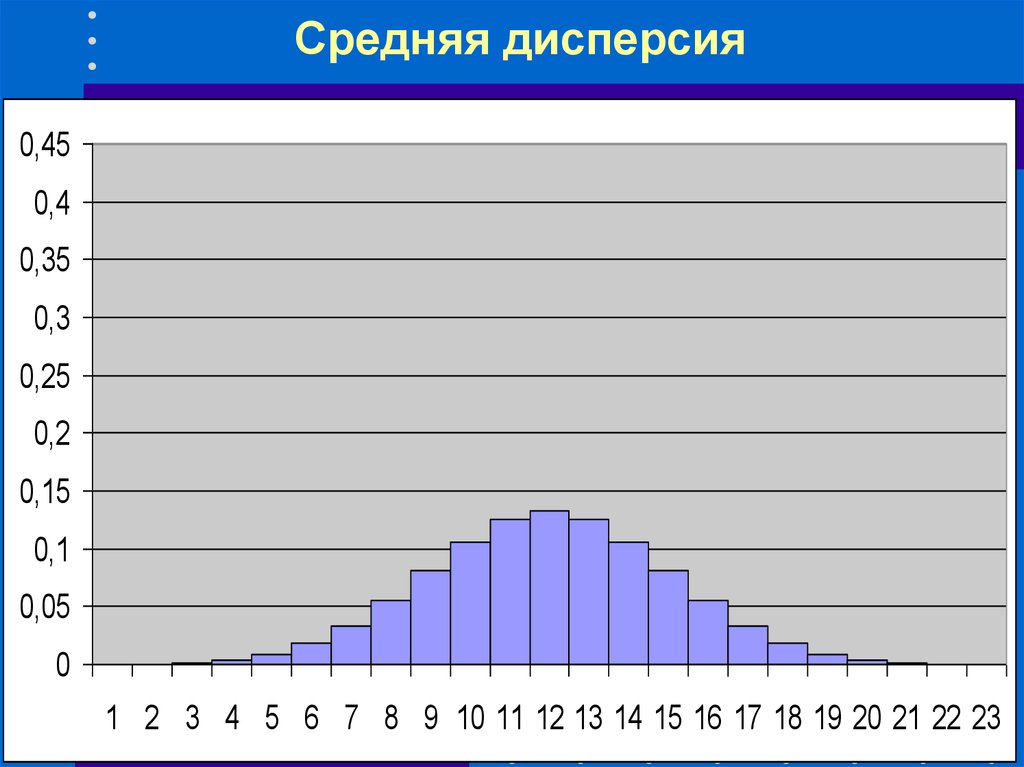
49. Средняя дисперсия

0,45
0,4
0,35
0,3
0,25
0,2
0,15
0,1
0,05
0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

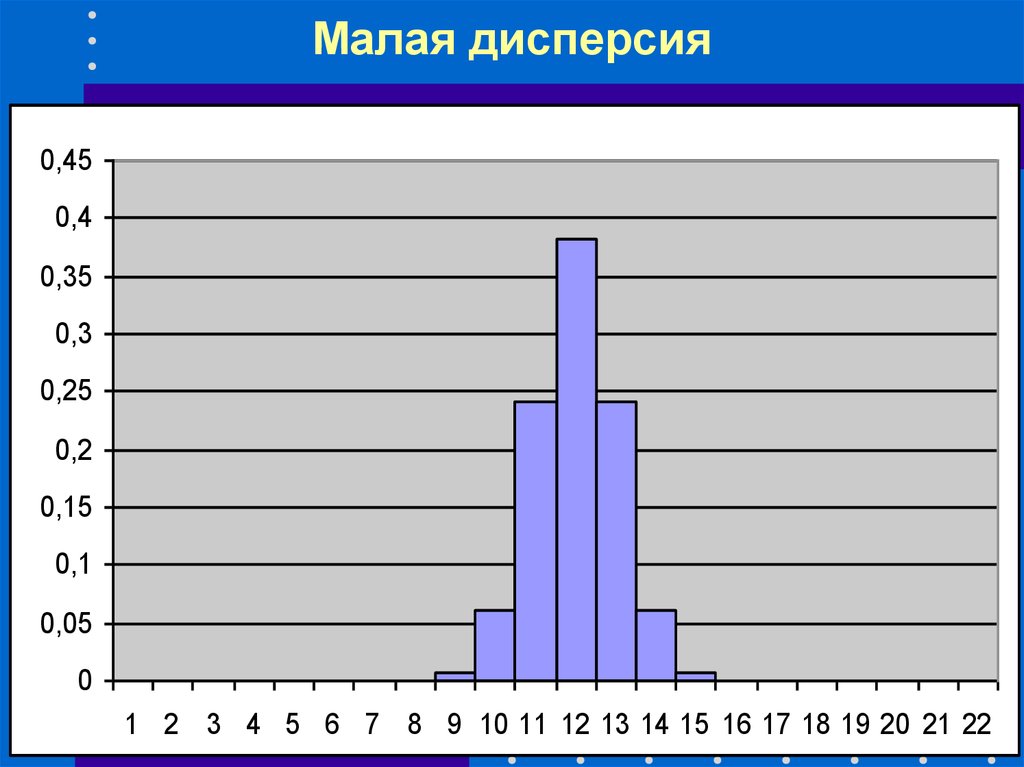
50. Малая дисперсия

0,45
0,4
0,35
0,3
0,25
0,2
0,15
0,1
0,05
0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

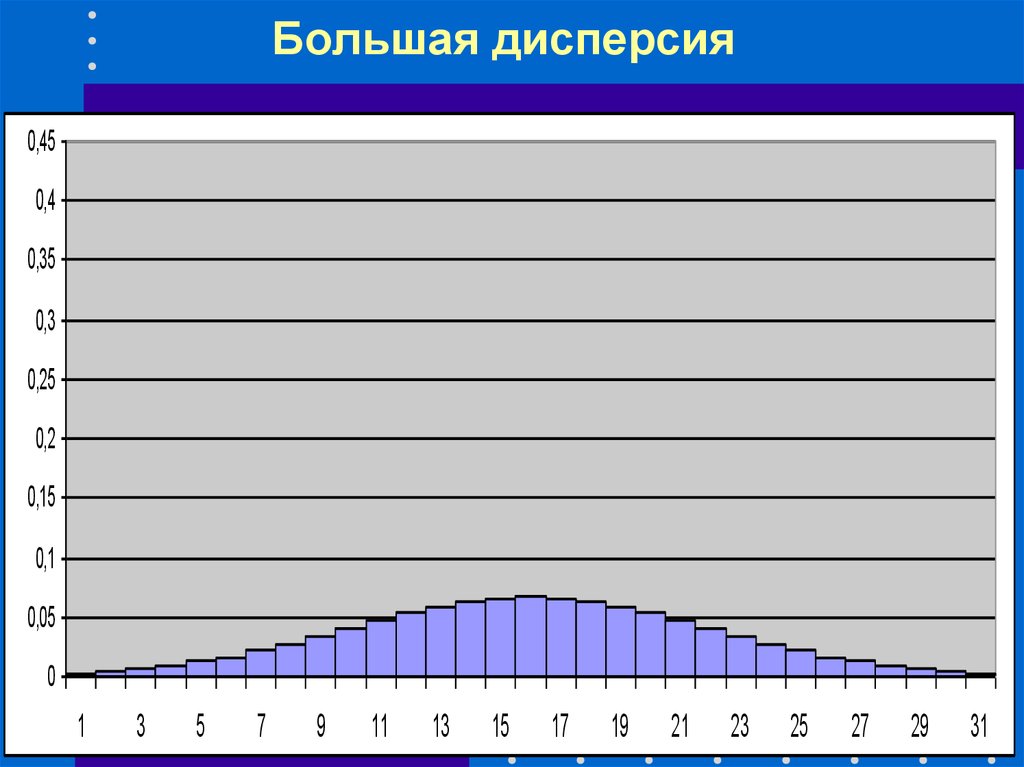
51. Большая дисперсия

0,45
0,4
0,35
0,3
0,25
0,2
0,15
0,1
0,05
0
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31

52. Среднее квадратическое откл.

=
2
1/2
( )
Преимущества:
• Измеряется в единицах варианты
• В предположении нормальности
варианты применимо правило k сигм
Удобно давать экономическую
интерпретацию

53. Коэффициент вариации

~
V = ( / X) 100%
• Только для положительных вариант
• Позволяет сравнивать степень
колеблемости показателей
• Совокупность считается
количественно однородной,
если V<33%