Similar presentations:
Однородная линия без потерь при гармонических напряжениях и токах
1. 15 лекция
Однородная линия без потерьпри гармонических
напряжениях и токах
2.
Однородная линия безпотерь при
гармонических
напряжениях и токах
2
3.
Линией без потерь считаетсялиния, у которой R0 << L0
и G0 << C0 , поэтому R0 0,
G0 0
3
4.
ТогдаZ 0 j L0
Z В ZВ
Y 0 j C0
Z0
Y0
L0
C0
Z 0 Y 0 j L0C0
4
5.
Таким образомL0C0
v 1
L0C0
0
2
2
L0C0
5
6.
Амплитуды падающей иотраженной волн напряжения
и тока вдоль линии меняться
не будут ( = 0)
6
7.
Будет изменяться фазанапряжения и тока вдоль
линии ( 0)
7
8.
Поскольку и v не зависятот , то линия без потерь
является линией без
искажений
8
9.
Так какch x ch j x cos x
sh x sh j x j sin x
9
10.
Тогда основные уравненияоднородной линии без потерь
при отсчете x от конца линии
будут следующими
10
11.
U x U 2 cos x jZ В I 2 sin xI x j U 2 sin x I cos x
2
ZВ
11
12. 14 лекция
Однородная линия без потерьпри гармонических
напряжениях и токах
13.
Если U 2 U 2 ej U 2
и
I 2 I2 e
j I 2
, то
мгновенные значения будут
следующими
13
14.
а) напряженияu x, t 2 U 2 cos x sin t U 2
2 I 2 Z В sin x sin t I 2 90
14
15.
б) токаi x, t
U2
2 sin x sin t U 2 90
ZВ
2 I 2 cos x sin t I 2
15
16.
Для любого момента временираспределение напряжения и
тока вдоль линии в функции x
является гармоническим
16
17.
а) t=t1u i
u( x, t1 )
i( x, t1 )
0
x
l
17
18.
а) t=t2u i u ( x , t2 )
0
i( x , t2 )
x
l
18
19.
Комплекс входногосопротивления линии
U1
Z H j Z В tg l
Z вх
ZВ
I1
Z В j Z Н tg l
U
где Z Н 2 - сопротивление
I2
нагрузки
19
20. Режимы однородной линии без потерь
2021.
Проанализируем длякомплексов действующих
значений напряжений и токов
с использованием основных
уравнений
21
22.
1 I1U1
1
I (x )
U (x )
l
I2 2
U2
x
ZН
2
22
23.
1. Режим холостого хода,когда
ZН = и I2 = 0
23
24.
U x U 2 cos xI x j U 2 sin x
ZВ
( хх )
Z вх j ZВ ctg l
24
25.
В линии стоячие волнынапряжения и тока
25
26.
Стоячие волны – эторезультат наложения
падающих и отраженных волн
с одинаковой амплитудой
26
27.
При стоячих волнах активнаямощность в любой точке
линии равна нулю
27
28.
При стоячих волнах пучностии узлы неподвижны и
сдвинуты друг относительно
друга на
4
28
29.
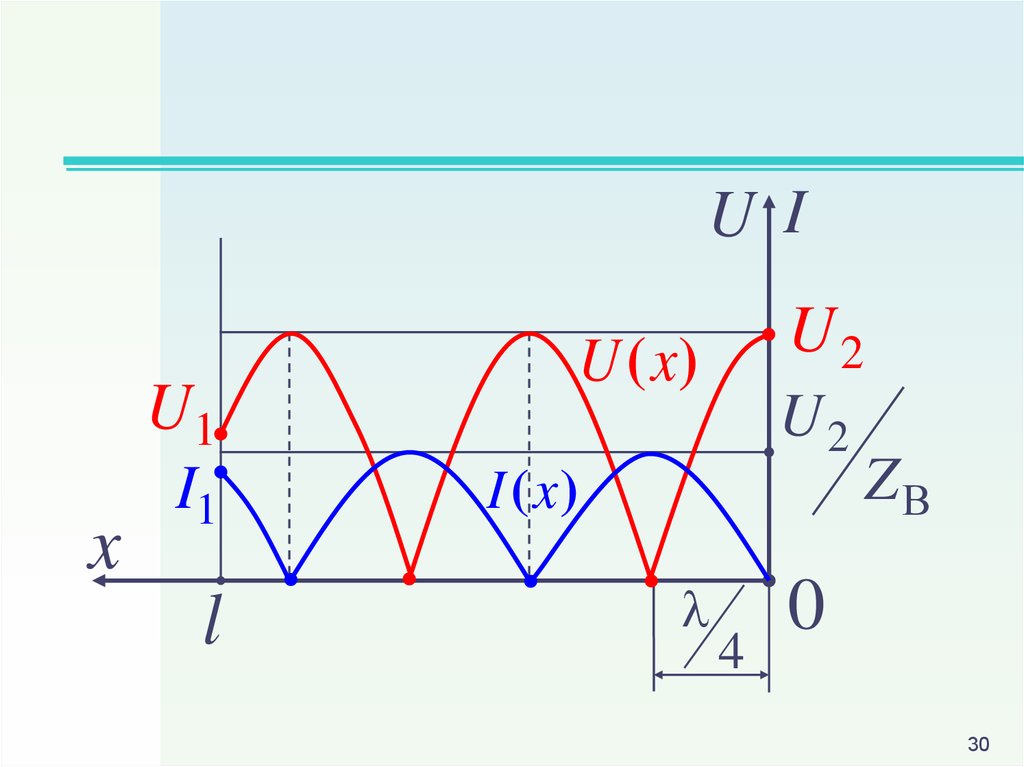
Построим графики длядействующих значений
U x U 2 cos x
U
I x 2 sin x
ZВ
29
30.
U IU1
x
I1
l
U2
U (x)
U2
I (x )
4
ZВ
0
30
31.
2. Режим короткогозамыкания, когда
ZН = 0
и U2 = 0
31
32.
U x j Z В I 2 sin xI x I 2 cos x
( кз )
Z вх
j ZВ tg l
32
33.
В линии – стоячие волныДействующие значения:
U x Z В I 2 sin x
I x I 2 cos x
33
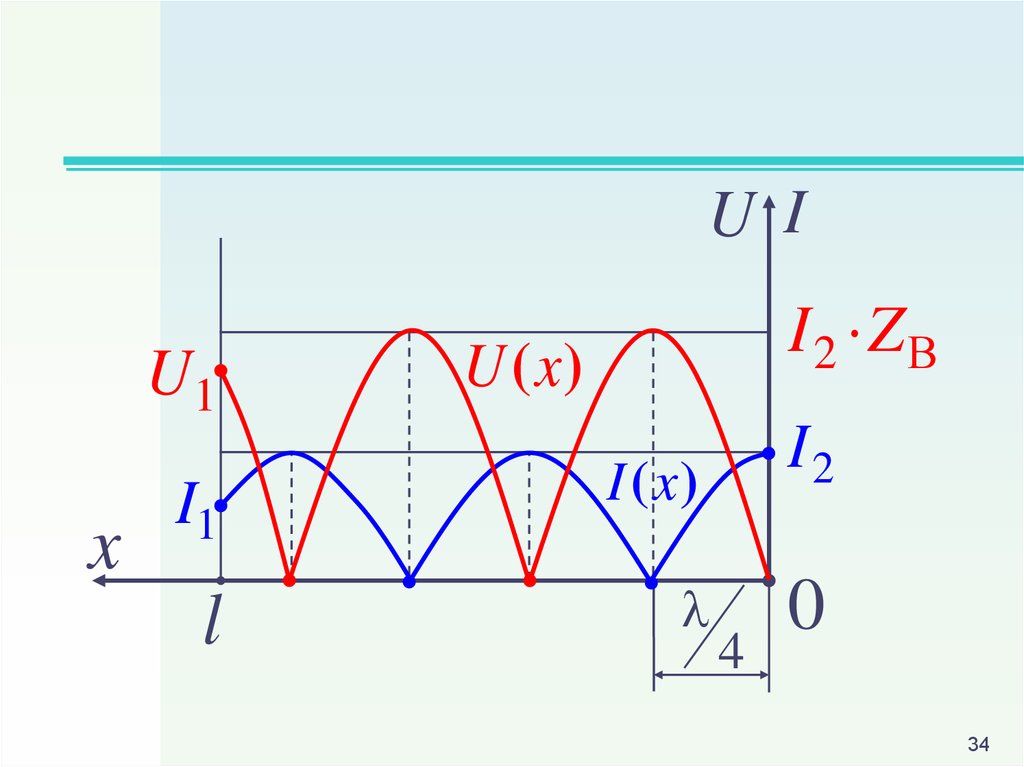
34.
U IU1
x
I2 ZВ
U (x)
I1
I (x )
I2
l
0
4
34
35.
3. Режим реактивнойнагрузки, когда ZН = j XH ,
U2 = j XH I2 , tg σ
XH
ZB
35
36.
sin xU
x
U
2
sin
cos
x
I x I 2
cos
36
37.
Входное сопротивление( р)
Z вх
tg l
j XH
tg
37
38.
В линии – стоячие волныДействующие значения:
sin x
U x U 2
sin
cos
x
I x I
2
cos
38
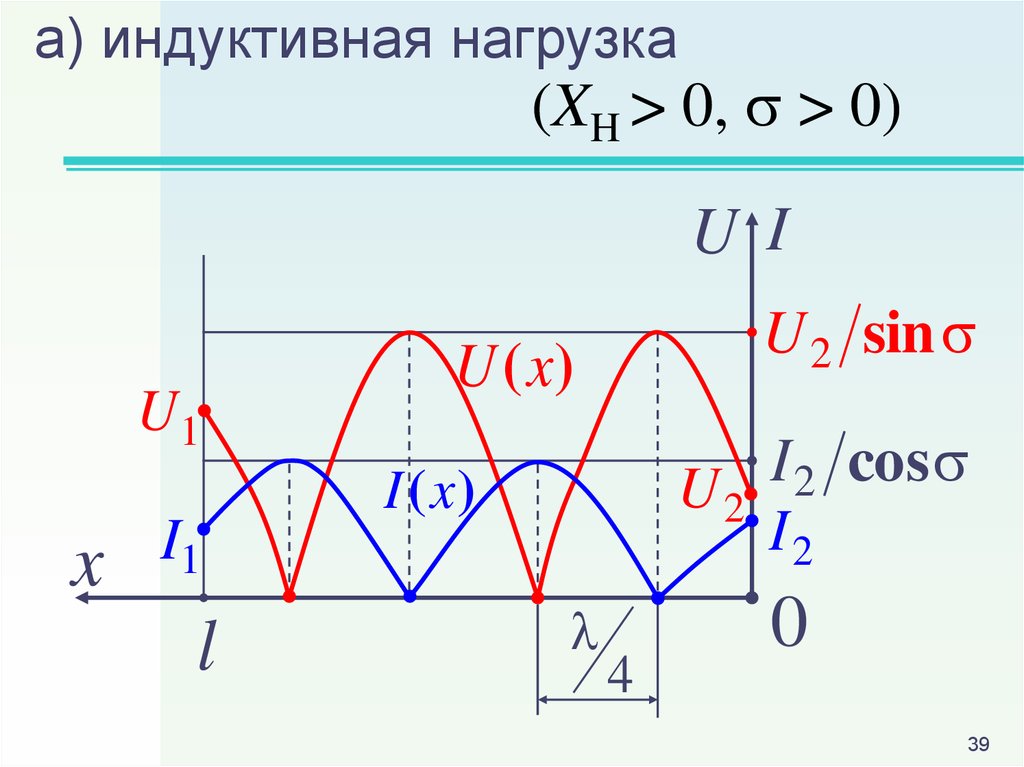
39.
а) индуктивная нагрузка(XH > 0, > 0)
U I
U1
x
I1
l
U 2 sin
U (x)
I
cos
2
U2
I (x )
I2
4
0
39
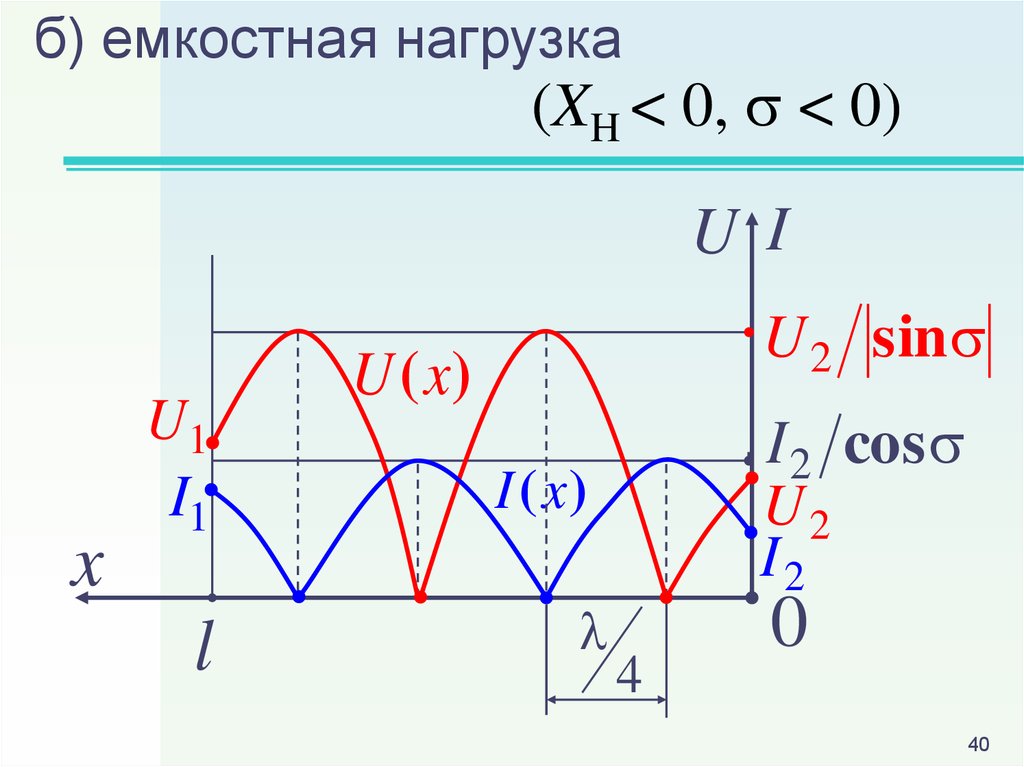
40.
б) емкостная нагрузка(XH < 0, < 0)
U I
x
U1
I1
l
U 2 sin
U (x)
I 2 cos
I (x )
U2
I2
4
0
40
41.
4. Режим согласованнойнагрузки, когда
Z H ZB
L0
C0
41
42.
U x U 2 e j xj x
I x I 2 e
(с)
Z вх ZВ
42
43.
Стоячих волн нетДействующие значения:
U x U 2
I x I 2
43
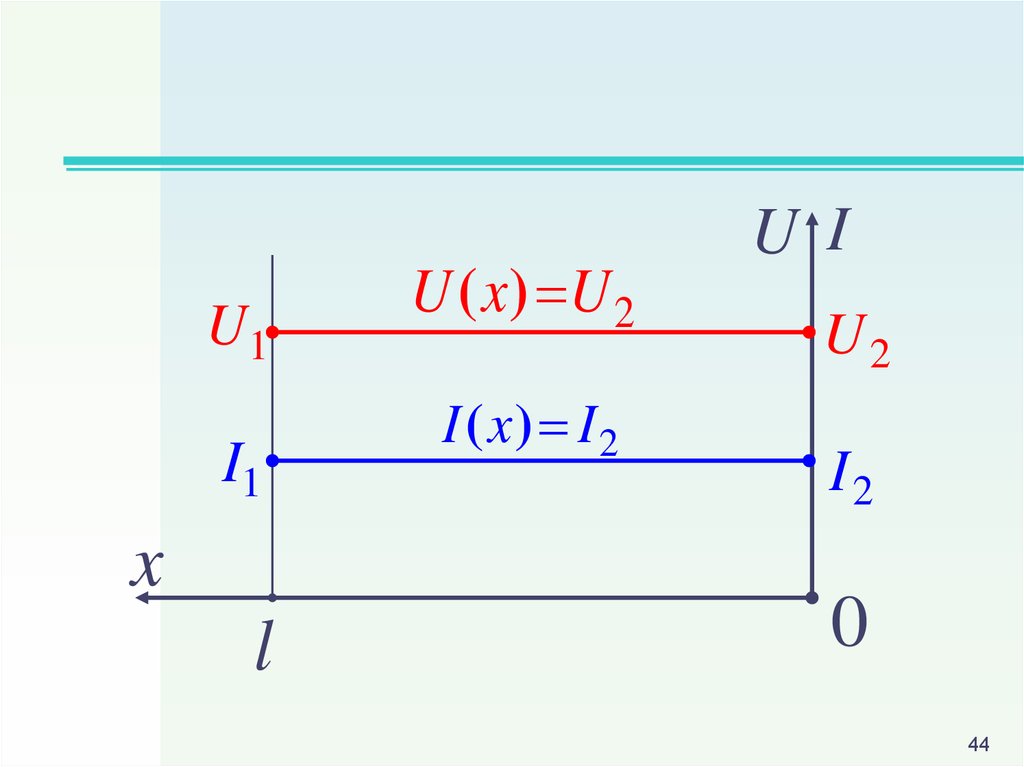
44.
U1I1
x
l
U ( x) U 2
I ( x) I 2
U I
U2
I2
0
44
45.
5. Режим активной нагрузки,когда
Z H RH Z B
45
46.
ZBsin x
U x U 2 cos x j
RH
R
I x I cos x j H sin x
2
ZB
46
47.
Стоячих волн нетДействующие значения:
2
ZB
2
2
U x U 2 cos x 2 sin x
RH
2
RH
2
2
I x I 2 cos x 2 sin x
Z
B
47
48.
а) RH < ZBU1
I1
x
l
U I
U (x)
U2
I2
I (x )
4
0
48
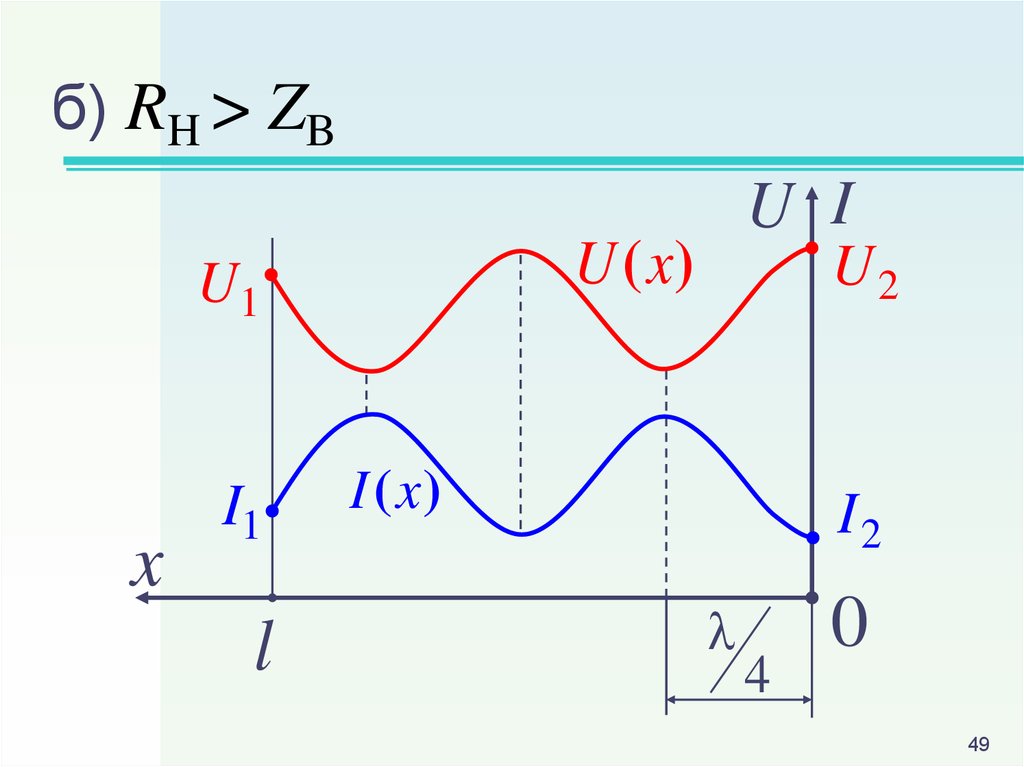
49.
б) RH > ZBU (x)
U1
x
I1
l
U I
U2
I (x )
I2
4
0
49
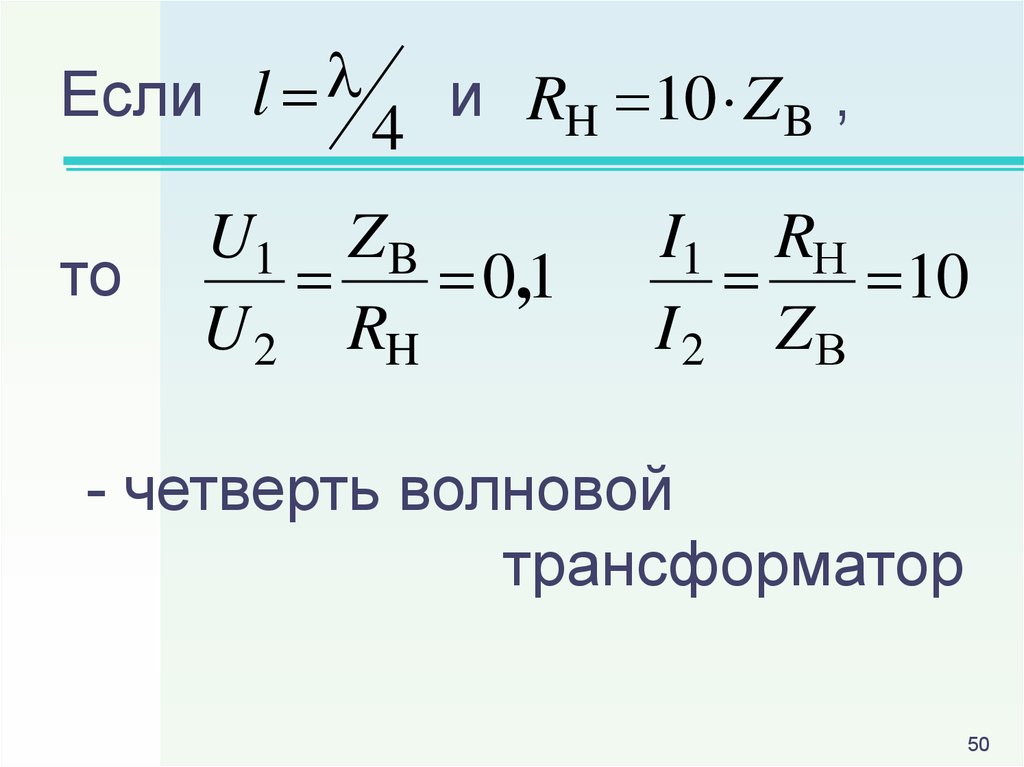
50.
Если lто
и RH 10 Z B ,
4
U1 Z B
0,1
U 2 RH
I1 RН
10
I2 ZВ
- четверть волновой
трансформатор
50










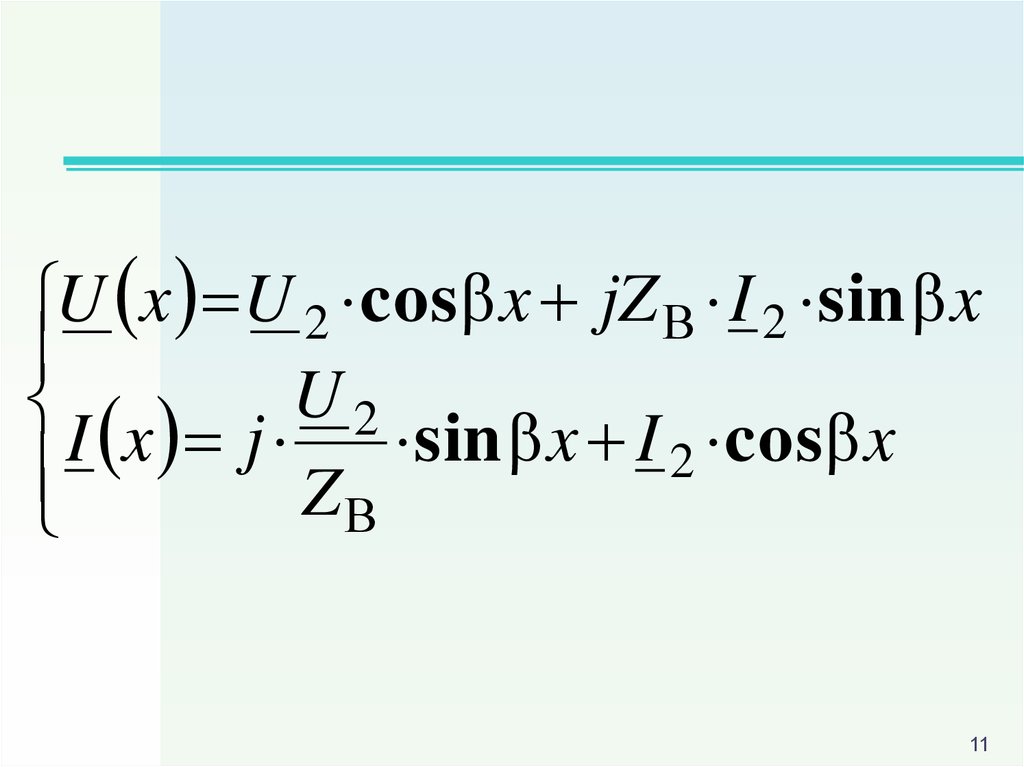












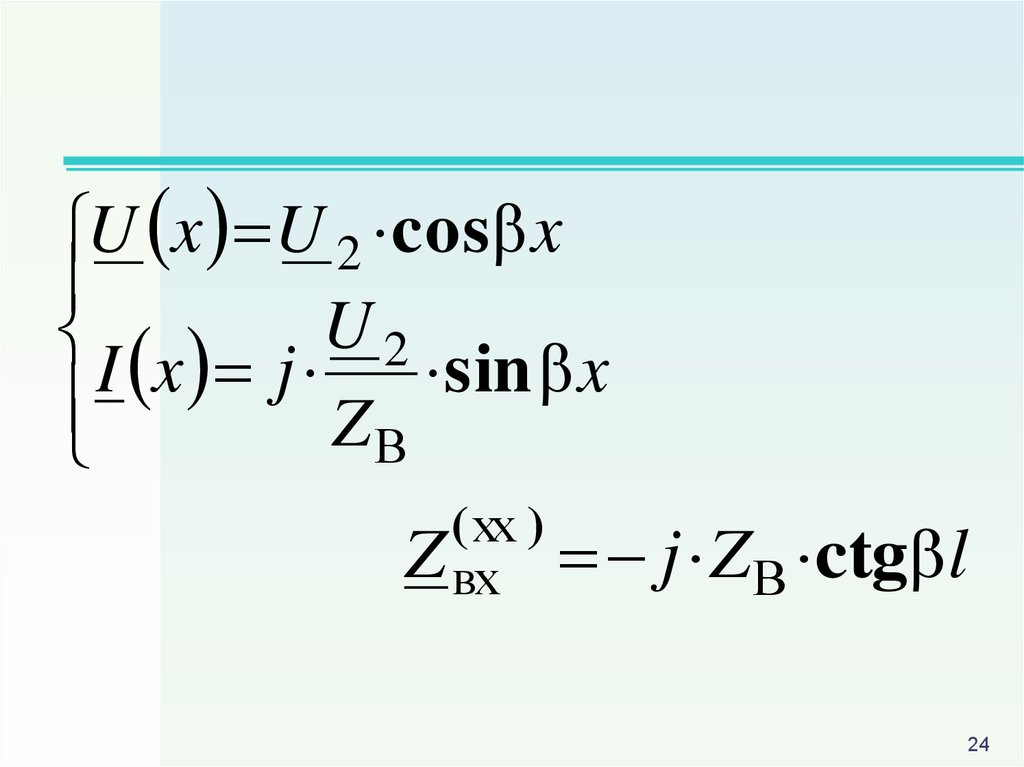






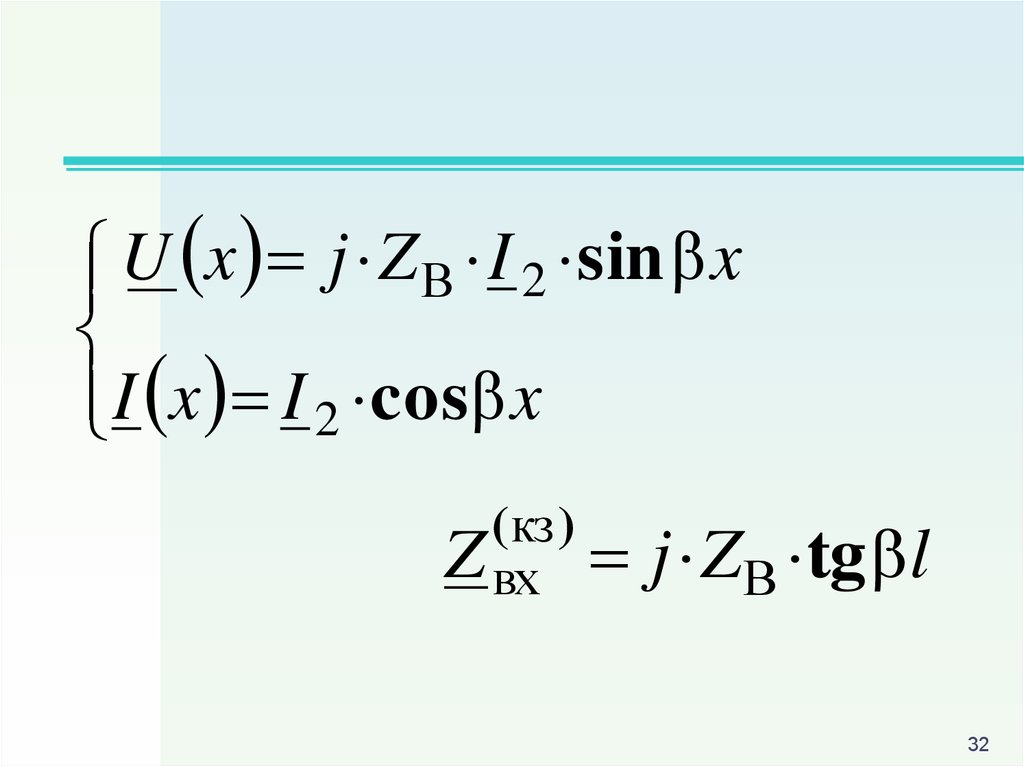


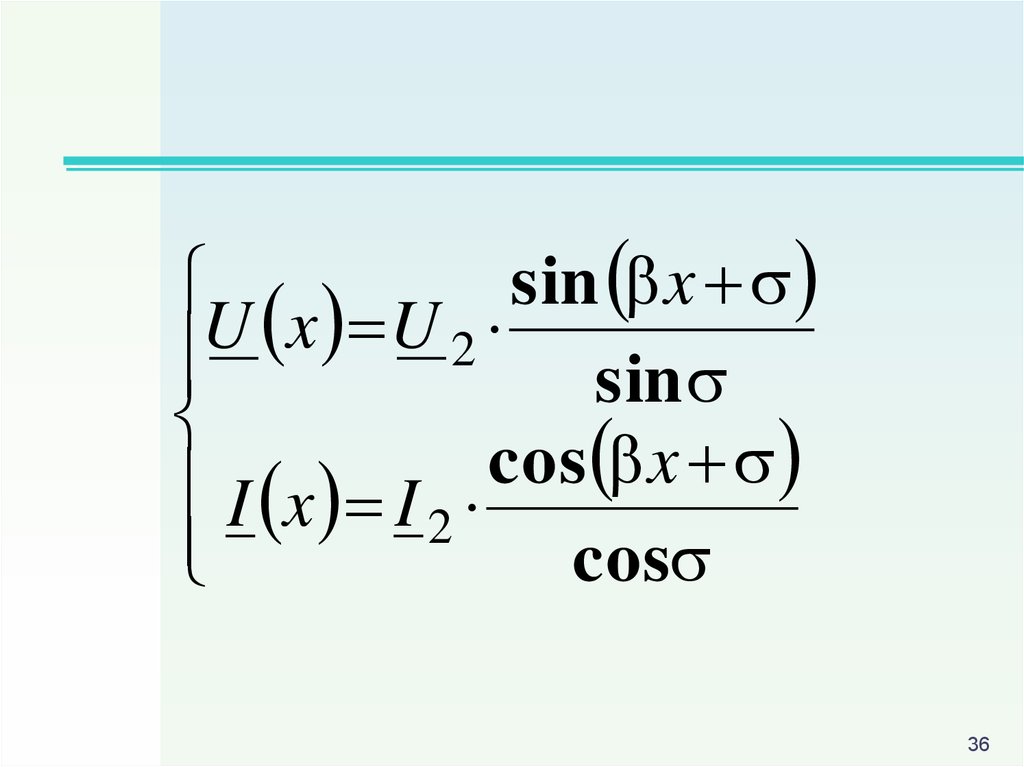



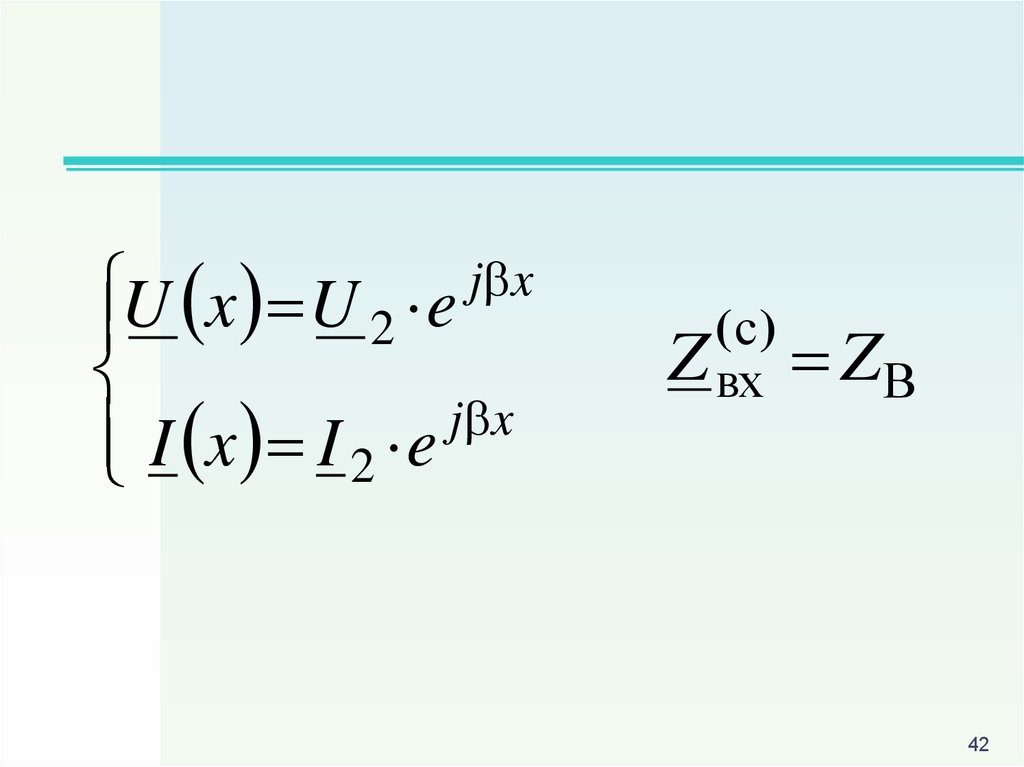


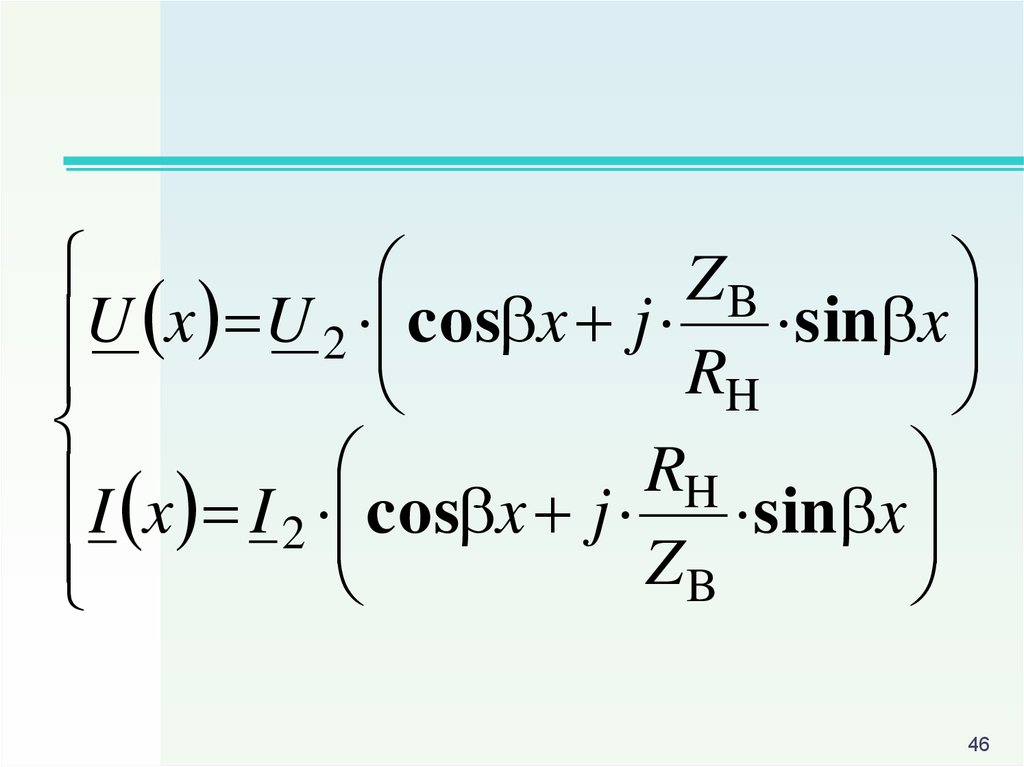


 electronics
electronics








