Similar presentations:
Гармонические токи и напряжения
1.
1. Атабеков Г.И. ТОЭ ч.1 §§ 2.1-2.3.2. Попов В.П. ОТЦ §§ 2.1.
2.
1. ВРЕМЕННОЕ ПРЕДСТАВЛЕНИЕГармонические токи и напряжения - это такие токи и
напряжения, которые изменяются во времени по
гармоническим законам
u (t ) U m cos( t u ) i(t ) I m cos( t i ),
(1)
где u(t ) - мгновенное значение напряжения; U m - амплитуда
напряжения (максимальное значение);
θ (t ) ωt ψu 2πt ψu - полная фаза напряжения;
2
= 2 f - круговая (угловая) частота, измеряет
T
скорость изменения фазы, рад/c;
1
f = - циклическая частота, Гц;
T
u - начальная фаза напряжения (фаза в начальный
момент времени t 0 ).
3.
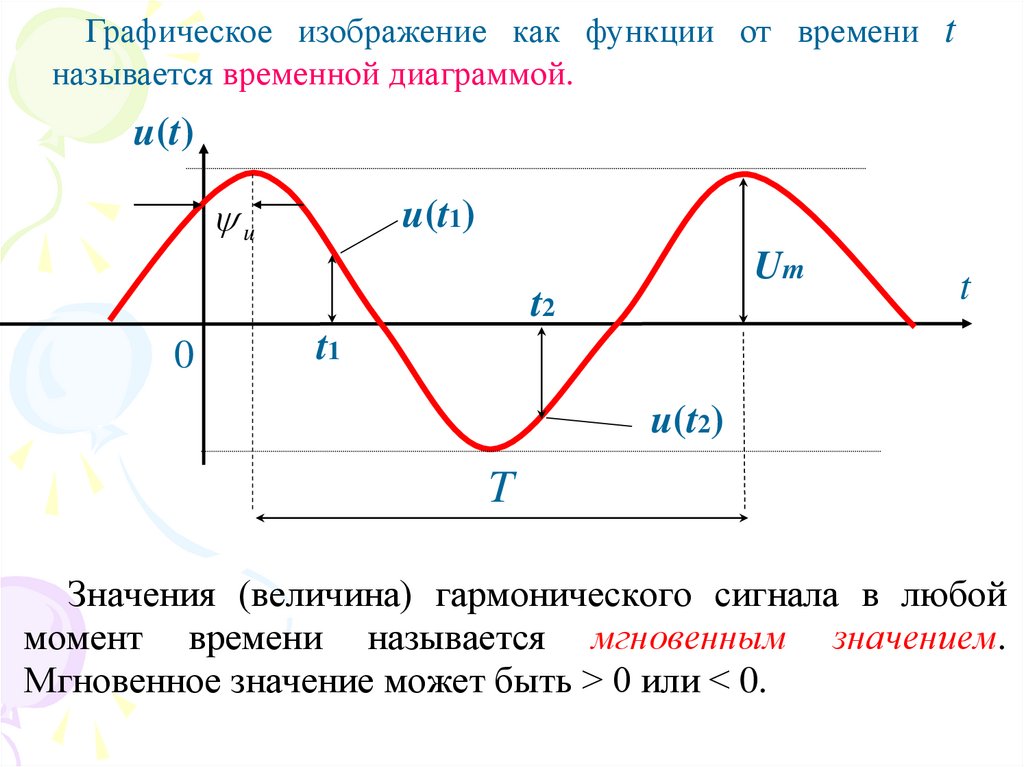
Графическое изображение как функции от времени tназывается временной диаграммой.
u(t)
u
u(t1)
Um
t2
0
t
t1
u(t2)
T
Значения (величина) гармонического сигнала в любой
момент времени называется мгновенным значением.
Мгновенное значение может быть > 0 или < 0.
4.
Гармоническийсигнал
характеризуется
3-мя
параметрами: - амплитудой Um, периодом повторения Т,
начальной фазой - u (величина определяющая значение
функции в t = 0, может быть > 0 или < 0.
Если первый положительный максимум расположен
левее оси ординат, то u > 0, если правее то u < 0.
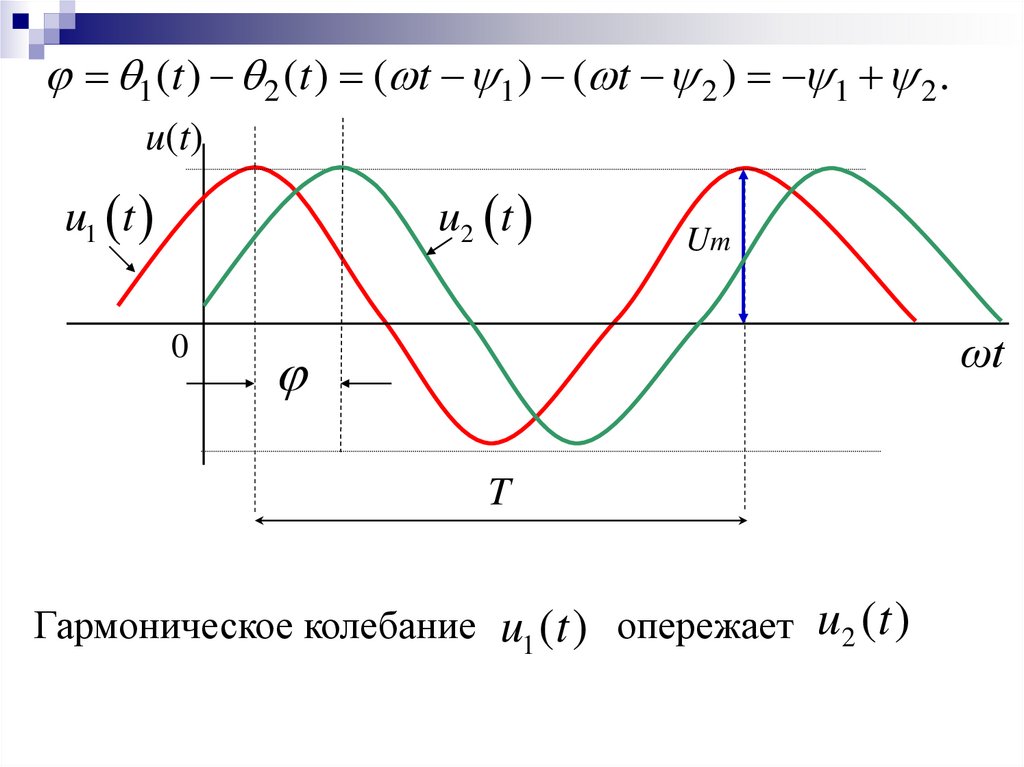
Если существуют два гармонических колебания, то
можно определить сдвиг фаз между ними.
φ θ1 (t ) θ2 (t )
Если сигналы изменяются с одной и той же
частотой, то равен разности начальных фаз и не
зависит от времени.
5.
1 (t ) 2 (t ) ( t 1 ) ( t 2 ) 1 2 .u(t)
u1 t
u2 t
0
Um
ωt
T
Гармоническое колебание u1 ( t ) опережает u2 ( t )
6.
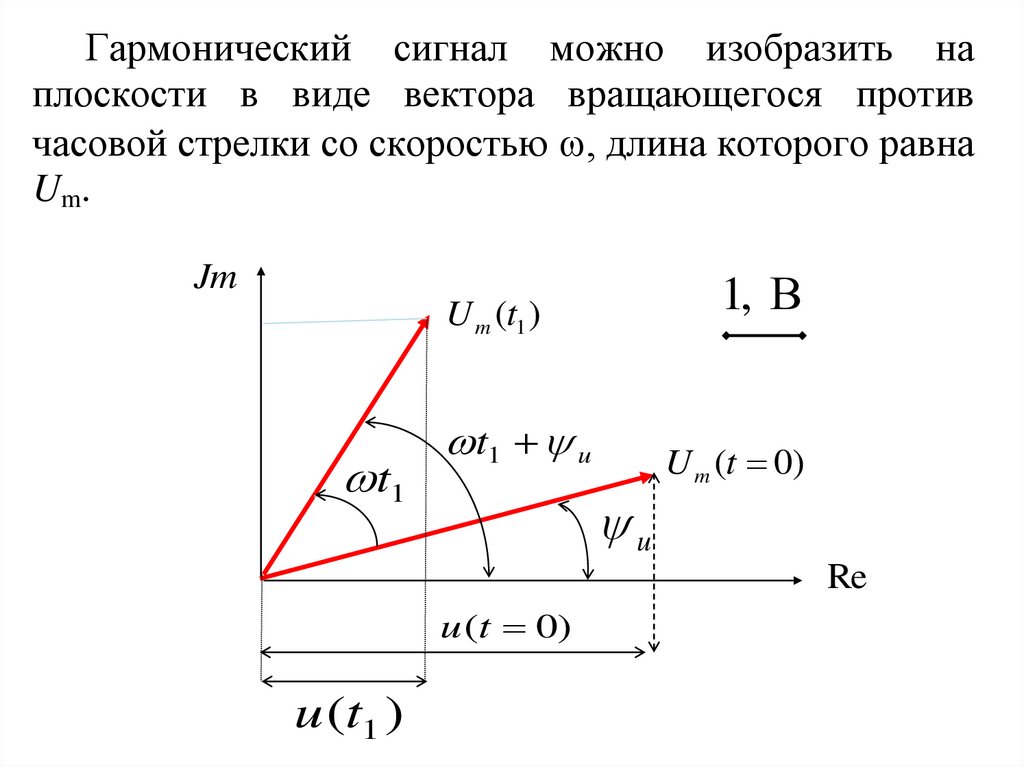
Гармонический сигнал можно изобразить наплоскости в виде вектора вращающегося против
часовой стрелки со скоростью , длина которого равна
Um.
Jm
1, В
U m (t1 )
t1
t1 u
U m (t 0)
u
Re
u (t 0)
u (t1 )
7.
Операции с гармоническими функциями прииспользовании
вращающегося
вектора
заменяются
операциями
над
векторами
(векторная алгебра).
При t = 0 вектор образует угол с положи-тельным
направлением оси абсцисс равный u . При u < 0
вектор вращается по часовой стрелке и наоборот.
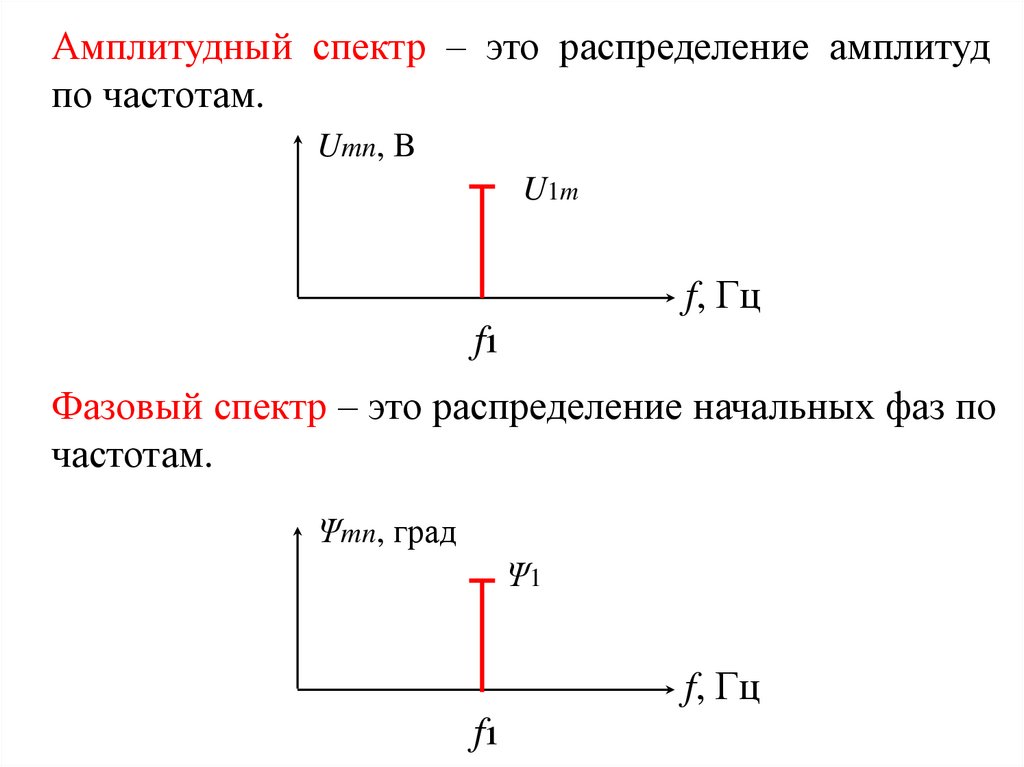
Гармонический сигнал можно изобразить как
функцию частоты в виде спектра гармонического
сигнала. В основе спектрального представления
сигнала лежат преобразования Фурье. Спектр
гармонического сигнала изображается в виде 2-х
диаграмм (спектров) амплитудного и фазового
спектров.
8.
Амплитудный спектр – это распределение амплитудпо частотам.
Umn, B
U1m
f, Гц
f1
Фазовый спектр – это распределение начальных фаз по
частотам.
Ψmn, град
Ψ1
f, Гц
f1
9.
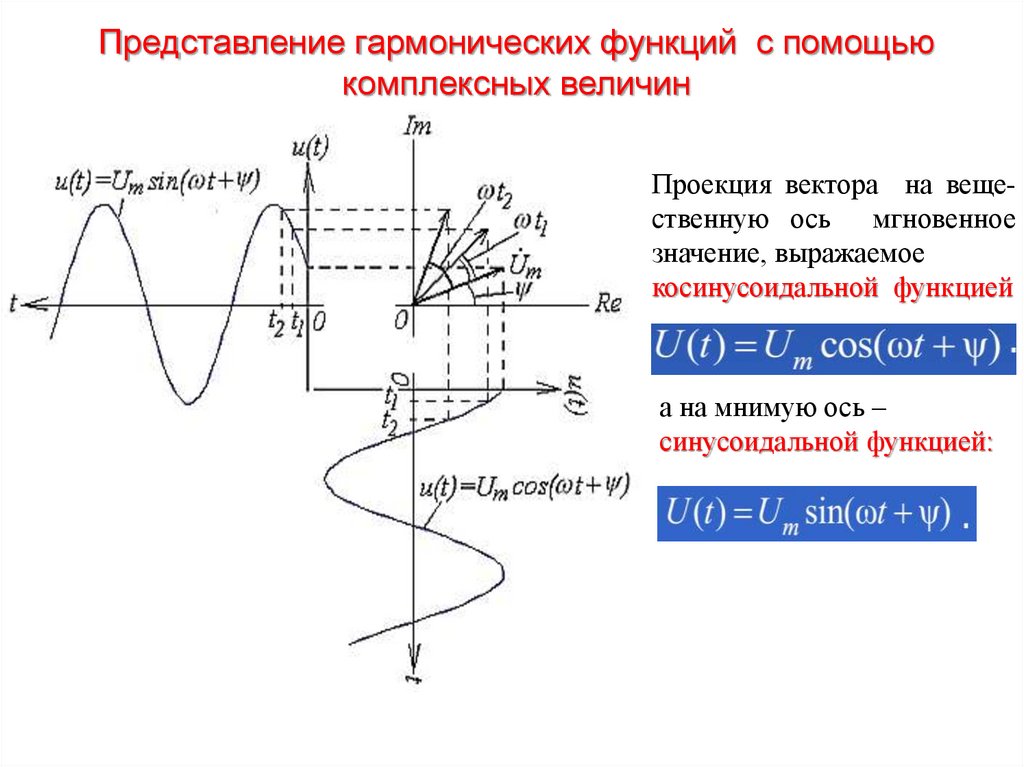
Представление гармонических функций с помощьюкомплексных величин
Проекция вектора на вещественную ось мгновенное
значение, выражаемое
косинусоидальной функцией
а на мнимую ось –
синусоидальной функцией:
10.
Символическийвектор
на
комплексной
плоскости
математически может быть представлен в трех формах:
алгебраической
показательной
тригонометрической
Модуль вектора
Аргумент
11.
Среднее и действующее значения гармоническогосигнала
Среднее значение любой периодической функции за период
определяется по формуле
T
1
Sср = S (t )dt.
Т0
Среднее значение гармонического сигнала за период Т равен 0.
Поэтому для гармонического сигнала среднее значение определяется
за Т/2 (или определяется среднее значение за период от функции
взятой по абсолютной величине).
T/2
T/4
1
2U m
U ср =
U mcosωt dt
sinωt dt =
T /2 0
Tω -T/4
2U m 2T 2
=
= U m 0,637U m .
T 2π
π
12.
Действующее(эффективное)
значение
среднеквадратичное значение переменного
-
это
T
I =
1
2
i
dt
.
T 0
Действующее значение характеризует
воздействие переменного тока.
T
RI T = R i di.
2
2
0
тепловое
13.
Найдем действующее значение гармоническоготока: i (t ) = I m sin(ωt ) .
I =
1T 2
2
I msin ωt dt =
T 0
2 T
Im
1 1
Im
.
( cos2ωt )dt =
T 0 2 2
2
Так
как
T
cos kωt dt = 0 ,
то
взяв
0
получим:
Im
I =
= 0,707 I m (A)
2
интеграл,
14.
Определим, как связаны амплитудное и среднее значение длягармонического тока.
T 2
2
2I m
I ср =
I msinωt =
0,637I m .
T 0
π
Среднее значение, обычно меньше действующего
Для характеристики кривых вводятся коэффициенты
Im
к амплитуды = к 0 =
= 2.
I
I mπ
π
к формы = к ф =
=
=
1,11.
I ср
2 2 Im
2 2
I
15.
Выводы:1. Гармоническое колебание может быть предс-тавлено в трёх
формах записи: в алгебраической, показательной
и
тригонометрической.
2. Гармоническое колебание может быть предс-тавлено
графически в виде временной, векторной и спектральной
диаграммах.
3. Значения гармонических токов и напряжений могут быть
амплитуднымиU m (I m ), среднимиUср (Iср ), действующими U(I).










 electronics
electronics








