Similar presentations:
Trigonometry. Angles add to 180°
1. Trigonometry
Executed: Bissarinova A.20-Aug-17
2. Angles add to 180°
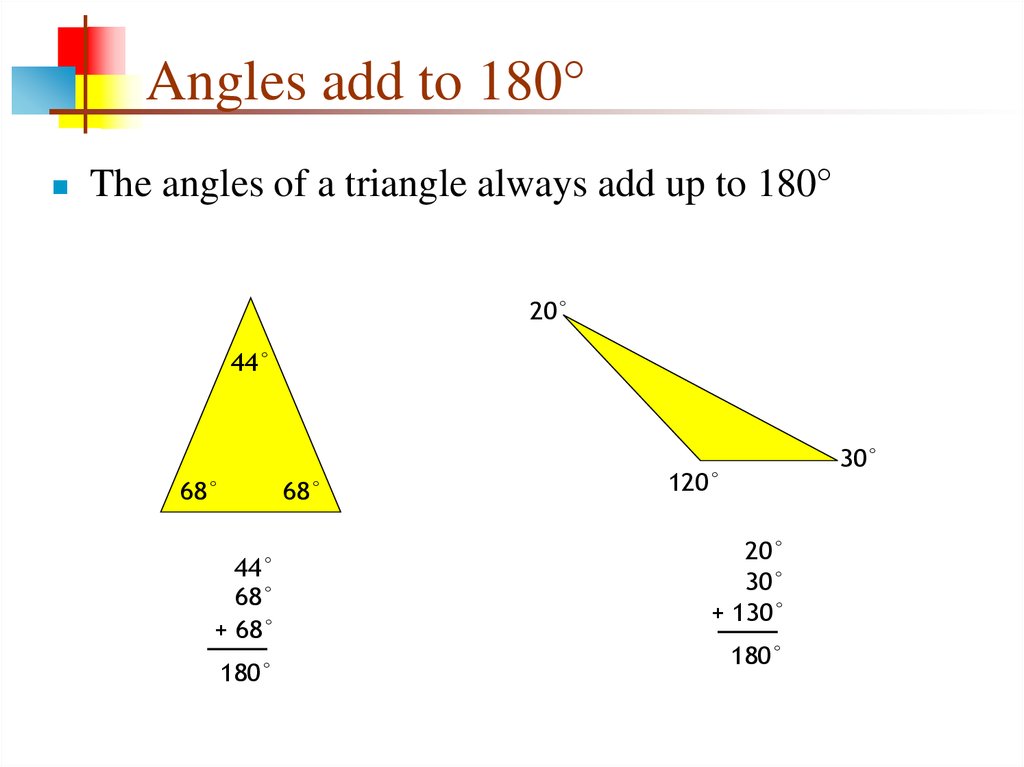
The angles of a triangle always add up to 180°20°
44°
68°
44°
68°
+ 68°
180°
68°
30°
120°
20°
30°
+ 130°
180°
3. Right triangles
We only care about right trianglesA right triangle is one in which one of the angles is 90°
Here’s a right triangle:
Here’s the angle
we are looking at
Here’s the
right angle
opposite
adjacent
We call the longest side the hypotenuse
We pick one of the other angles--not the right angle
We name the other two sides relative to that angle
4. Example.
Solve the equations:a) cos (x / 5) = 1
Decision: A) This time
we proceed directly to the
calculation of the roots of
the equation at once: x / 5
= ± arccos (1) + 2πk.
Then x / 5 = πk => x = 5πk
The answer is: x = 5πk,
where k is an integer.
b) tg (3x-π / 3) = √3
B) We write in the form:
3x-π / 3 = arctg (√3) +
πk. We know that: arctg
(√3) = π / 3 3x-π / 3 = π /
3 + πk => 3x = 2π / 3 +
πk => x = 2π / 9 + πk / 3
The answer is: x = 2π / 9
+ πk / 3, where k is an
integer.
5. The Pythagorean Theorem
If you square the length of thetwo shorter sides and add
them, you get the square of the
length of the hypotenuse
adj2 + opp2 = hyp2
32 + 42 = 52, or 9 + 16 = 25
hyp = sqrt(adj2 + opp2)
5 = sqrt(9 + 16)
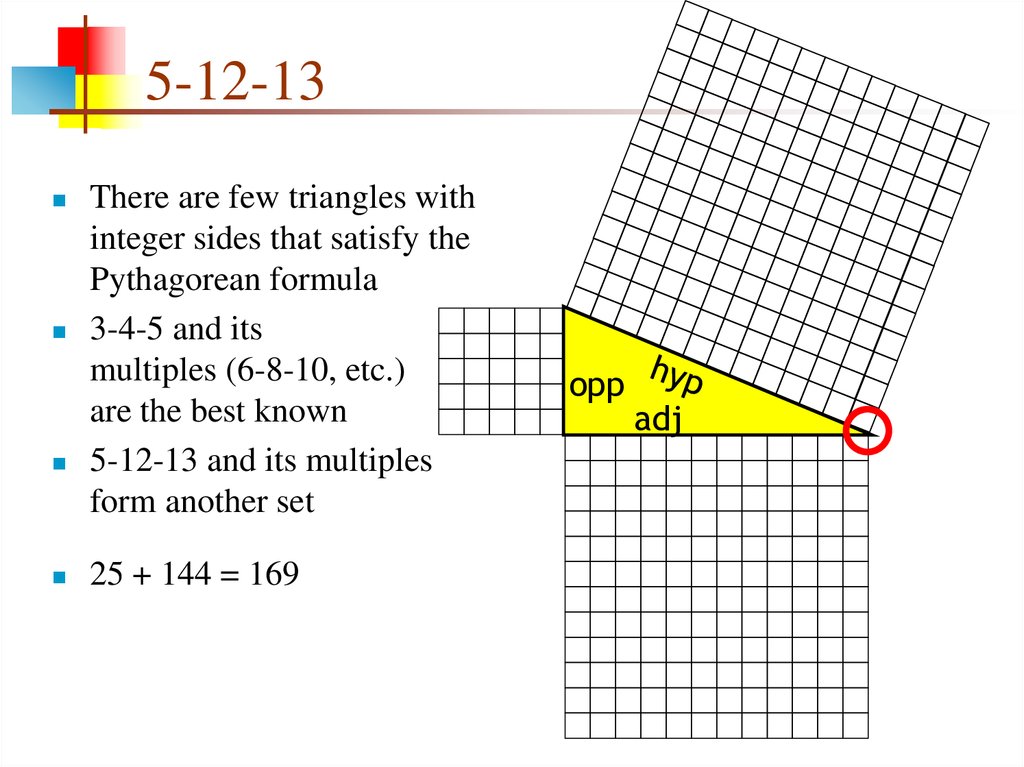
6. 5-12-13
There are few triangles withinteger sides that satisfy the
Pythagorean formula
3-4-5 and its
multiples (6-8-10, etc.)
are the best known
5-12-13 and its multiples
form another set
25 + 144 = 169
opp
adj
7. Ratios
Since a triangle has threesides, there are six ways to
divide the lengths of the sides
Each of these six ratios has a
name (and an abbreviation)
Three ratios are most used:
sine = sin = opp / hyp
cosine = cos = adj / hyp
tangent = tan = opp / adj
The other three ratios are
redundant with these and can
be ignored
opposite
opposite
Ratios
adjacent
The ratios depend on the
shape of the triangle (the
angles) but not on the size
adjacent
8. Example.
Solve the equations:cos (4x) = √2 / 2.
And find all the roots on the
interval [0; Π].
Decision: Let us solve our equation
in general form: 4x = ± arccos (√2 /
2) + 2πk 4x = ± π / 4 + 2πk;
X = ± π / 16 + πk / 2;
Now let's see what roots get into
our segment.
When k <0, the solution is also less
than zero, we do not fall into our
segment.
For k = 0, x = π / 16, we are in the
given interval [0; Π].
For k = 1, x = π / 16 + π / 2 = 9π / 16,
again we have got.
For k = 2, x = π / 16 + π = 17π / 16,
and here we are no longer there, and
therefore for large k we also will not
fall.
The answer is: x = π / 16, x = 9π / 16
9. Using the ratios
With these functions, if you know an angle (in addition to theright angle) and the length of a side, you can compute all other
angles and lengths of sides
opposite
adjacent
If you know the angle marked in red (call it A) and you know
the length of the adjacent side, then
tan A = opp / adj, so length of opposite side is given by
opp = adj * tan A
cos A = adj / hyp, so length of hypotenuse is given by
hyp = adj / cos A
10. Solve equations:
а) cos(x/5)=1The answer is: x = 5πk,
where k is an integer.
б)tg(3x- π/3)= √3
The answer is: x = 2π / 9
+ πk / 3, where k is an
integer.
11.
Decision: A) This time weproceed directly to the
calculation of the roots of the
equation at once:
x / 5 = ± arccos (1) + 2πk.
Then x / 5 = πk => x = 5πk
The answer is: x = 5πk,
where k is an integer.
B) We write in the form: 3x-π
/ 3 = arctg (√3) + πk.
We know that:
arctg (√3) = π / 3 3x-π / 3 = π
/ 3 + πk => 3x = 2π / 3 + πk
=> x = 2π / 9 + πk / 3
The answer is:
x = 2π / 9 + πk / 3, where k is
an integer
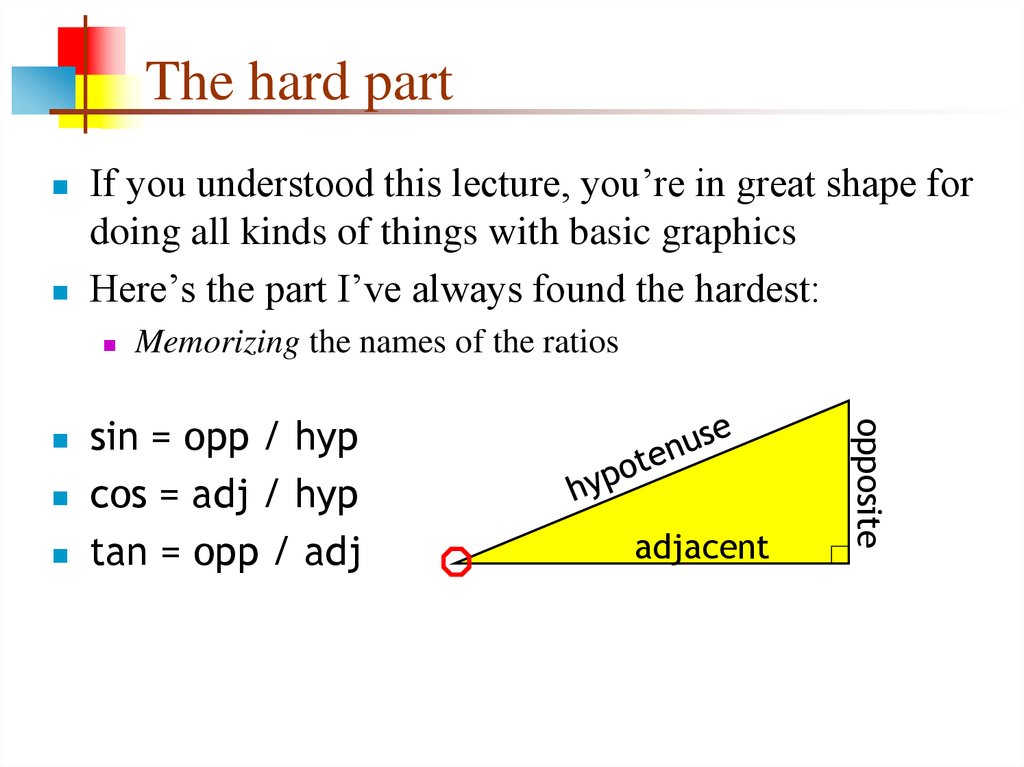
12. The hard part
If you understood this lecture, you’re in great shape fordoing all kinds of things with basic graphics
Here’s the part I’ve always found the hardest:
sin = opp / hyp
cos = adj / hyp
tan = opp / adj
adjacent
opposite
Memorizing the names of the ratios










 mathematics
mathematics








