Similar presentations:
Принцип возможных перемещений (§1 - §6)
1. Глава 4 Принцип возможных перемещений
§ 1. Классификация связей§ 2. Возможные перемещения системы
§ 3. Принцип возможных перемещений
§ 4. Решение задач с помощью ПВП
§ 5. Общие уравнения динамики
§ 6. Примеры решения задач
2.
§ 1. Классификация связейСвязями называются любого вида ограничения,
которые накладываются на положения и скорости точек
механической системы и выполняются независимо от
того, какие на систему действуют силы
Стационарные связи
Нестационарные связи
Геометрические связи
Кинематические связи
Интегрируемые связи
Неинтегрируемые связи
Голономные связи
Неголономные связи
(дифференциальные)
3.
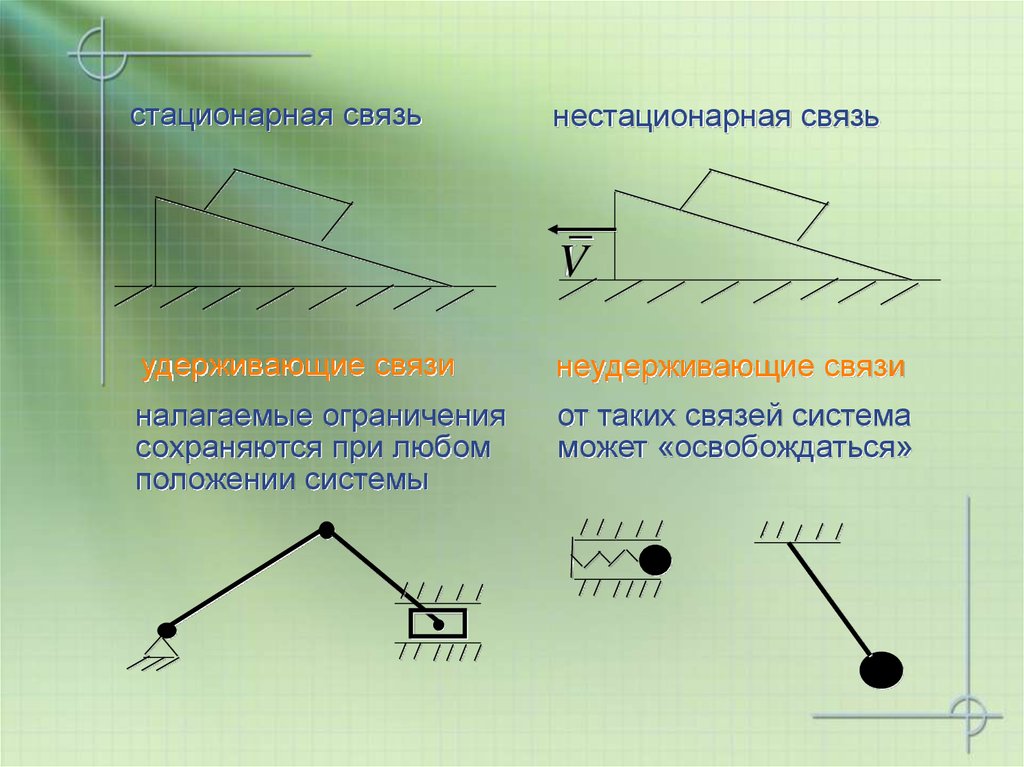
стационарная связьнестационарная связь
V
удерживающие связи
неудерживающие связи
налагаемые ограничения
сохраняются при любом
положении системы
от таких связей система
может «освобождаться»
4. § 2. Возможные перемещения системы
Влияние связей1. Появление сил реакции
2. Перемещения, которые могут иметь точки системы
Возможным перемещением механической системы
будем называть любую совокупность элементарных
перемещений точек этой системы из занимаемого в
данный момент времени положения, которые
допускаются всеми наложенными на систему связями
r x, y, z
Перемещения должны быть элементарными, чтобы вид
связи не изменился
Вид связи не должен измениться, даже при
элементарном перемещении
5. Возможные перемещения характеризуются тем, что
могут и не происходить (воображаемые)бесконечно малые
происходят с сохранением всех наложенных на
систему связей
не происходят во времени (δt = 0)
Действительные перемещения
dr
бесконечно малые
происходят с сохранением всех наложенных на
систему связей
происходят за некоторый промежуток времени
6.
В случае голономных, идеальных, стационарныхсвязей действительные перемещения являются частью
виртуальных
В случае нестационарных связей действительные
перемещения не совпадают ни с одним из виртуальных
перемещений
Движущийся лифт
V
δφ=dφ
δу
δs=ds
dr
δх
7. Механическая система одновременно может иметь несколько возможных перемещений
Число независимых между собой возможныхперемещений механической системы называется
числом степеней свободы этой системы
У механической системы с геометрическими связями
число независимых координат, определяющих
положение системы, совпадает с числом ее степеней
свободы
Чтобы определить число степеней свободы, нужно
последовательно предотвращать возможные
перемещения
8.
угол тангажаугол крена
угол рыскания
δφ=dφ
δу
δs=ds
δr
δх
9.
§ 3. Принцип возможных перемещенийУстанавливает общее условие равновесия
механической системы в целом
При идеальных связях позволяет исключить из
рассмотрения все наперед неизвестные реакции связей
Выполняется в инерциальных системах отсчета
Все точки системы под действием приложенных сил
находятся в покое по отношению к инерциальной
системе отсчета («абсолютное равновесие»)
10. Все связи будем считать стационарными
Возможная работа – это элементарная работа,которую действующая на материальную точку сила
могла бы совершить на перемещении, совпадающем с
возможным перемещением этой точки ( δ A = F ∙ δ r )
δ Aa = Fa ∙ δ r
− возможная работа активных сил
δ Ar = N ∙ δ r
− возможная работа реакций
связей
Связь называется идеальной, если работа реакций
этих связей на любых возможных перемещениях
равнялась нулю или была бы больше нуля (Σδ Ar ≥ 0)
11.
Постулат идеальных связей в 1806 году сформулировалАндре Мари Ампер
Андре-Мари Ампер
(фр. Andre Marie Ampere;
22 января 1775 —
10 июня 1836) — знаменитый
французский математик и
естествоиспытатель
12.
Принцип возможных перемещений (ПВП) первым бездоказательства сформулировал Иоганн Бернулли
Иоганн Бернулли
(нем. Johann Bernoulli,
27 июля 1667, Базель,
Швейцария —
1 января 1748, там же) —
один из величайших
математиков своего времени
13.
Принцип возможных перемещений (ПВП)Первым доказал и сформулировал в общем виде в
1788 году Жозеф Луи Лагранж
Для удерживающих связей
A
r
k
0
k
Обобщил на случай неудерживающих связей в
1838−1842 годах Михаил Васильевич Остроградский
Для освобождающихся связей
A
r
k
k
0
14. Жозеф Луи Лагранж (фр. Joseph Louis Lagrange 25 января 1736, Турин – 10 апреля 1813, Париж) – французский математик и механик
15.
Михаил Васильевич Остроградский(12(24) сентября 1801−20 декабря 1861(1 января 1862)
− российский и украинский математик и механик,
признанный лидер математиков Российской империи
середины XIX века
16.
Для равновесия механической системы с идеальнымисвязями необходимо и достаточно, чтобы сумма
элементарных работ всех действующих на неё
активных сил при любом возможном перемещении
системы была равна нулю в случае удерживающих
связей и меньше нуля в случае неудерживающих связей
A
a
k
0
− уравнение возможных работ
k
Уравнение возможных работ в аналитической форме
a
a
a
F
x
F
y
F
kx k ky k kz zk 0
k
17.
Необходимость:Пусть механическая система находится под действием
внешних сил, главный вектор которых R
F
k
k
На неё наложены голономные, стационарные связи
N Nk
k
Тогда для каждой точки системы уравнения равновесия
Fk Nk 0 rk Fk rk Nk rk 0
Просуммируем по всем точкам системы
F r
k
k
N k rk 0 Fk rk N k rk 0
k
k
По постулату идеальных связей
Fk rk 0 или
k
k
N r
A 0
k
k
a
k
k
k
0,
18.
Достаточность:Пусть механическая система с идеальными связями,
удовлетворяющая неравенству
Aka 0 (*),
k
drk , тогда
dT dAka Fka drk 0
совершает действительное перемещение
k
k
При стационарных связях действительные
перемещения совпадают с какими-либо возможными и
a
a
dA
A
k k 0
k
k
Но это противоречит условию (*)
Когда приложенные силы к системе удовлетворяют
условию (*), система из состояния покоя выйти не может,
следовательно, это условие является достаточным
условием равновесия системы
19. Если не все связи, наложенные на систему, являются идеальными, например, негладкие опорные поверхности, то к задаваемым силам следует добав
Если не все связи, наложенные на систему, являютсяидеальными,
например,
негладкие
опорные
поверхности, то к задаваемым силам следует добавлять
силы трения. Тогда уравнение ПВП будет определять
зависимость между задаваемыми силами и силами
трения.
Если требуется определить какую-либо силу реакции
идеальной связи, для которой R∙δr = 0, то следует,
применяя принцип освобождаемости от связей,
отбросить связь и заменить её искомой силой реакции.
При составлении уравнения равновесия надо к
задаваемым силам добавить эту силу реакции связи.
Искомую величину определить из составленного
уравнения равновесия.
ПВП устанавливает общее условие равновесия
механической системы и позволяет при идеальных
связях исключать из рассмотрения все наперед
неизвестные реакции связей
20. § 4. Решение задач с помощью ПВП
а) определяют степени свободыДля этого останавливают поступательное или
вращательное движение одного звена механической
системы, если она становится неподвижной, то, значит,
имеет лишь одну степень свободы.
Если система не становится неподвижной после
остановки
первого
звена,
то
останавливают
поступательное или вращательное движение второго
звена механической системы. Если она становится
неподвижной, то имеет две степени свободы. И так
далее…
б) решают задачу аналитически или геометрически
21. План решения геометрическим способом в случае, когда система обладает одной степенью свободы
1. Изобразить все активные силы2. Показать на чертеже всем звеньям системы
возможные перемещения δφk и δsk
3. Вычислить элементарные работы:
Aka Fka dsk cos k ,
Aka M ka d k
4. Графически выразить все перемещения δφk и δsk
через одно
a
A
k 0
5. Составить уравнение ПВП:
k
6. Определить искомую величину
22. План решения аналитическим способом в случае, когда система обладает одной степенью свободы
1. Оси координат связать с телом, которое при любыхвозможных перемещениях остается неподвижным.
Изобразить все заданные силы
2. В случае неидеальных связей добавить
соответствующие силы реакций связи
3. Задать возможное перемещение одной из точек
системы (δφk или δsk) и выразить возможные
перемещения точек приложения сил в зависимости от
выбранного δφk или δsk
4. Вычислить элементарные работы:
Aka Fka dsk cos k ,
Aka M ka d k
a
A
5. Составить уравнение ПВП: k 0
k
6. Определить искомую величину
23. Пример 1
ВF
δs
В
Пример 1
В механизме (рычажный
подъемник) найти зависимость
между силами F и Q при равновесии
Решение
1. У системы 1 степень свободы
δs
А
А
Q
О
3. Возможные перемещения δsА и δsВ
Так как ОВ = 3 ОА, после
дифференцирования δsВ = 3 δsА
4. δА(F) = F ∙ δsB и δА(Q) = Q ∙ δsА
5. F ∙ δsB − Q ∙ δsА = 0,
sB
3F
6. Q F
s A
24. Пример 2
Вес бревна Q, вес каждого из двух цилиндрическихкатков, на которые оно положено, – Р. Определить,
какую силу F надо приложить к бревну, чтобы удержать
его в равновесии на наклонной плоскости при заданном
угле наклона α. Трение катка о плоскость и бревно
обеспечивает отсутствие скольжения
Решение
F
δs
БQ
α
Р
δsК
Р
1. У системы 1 степень свободы
3. Возможные перемещения δsК и δsБ
Так как VБ = 2 VК, то δsБ = 2 δsК
4. δА(F) = F ∙ δsБ и
δА(Q) = −Q ∙ δsБ∙ sinα ,
δА(Р) = −Р ∙ δsК∙ sinα
5. F ∙ δsБ − Q ∙ δsБ sinα −
− 2P ∙ δsК sinα = 0,
6. F Q P sin
25. Пример 3
По заданным активным силам найти неизвестнуюреакцию NВ
Решение
РД
С
В
А
1. У системы 1 степень свободы
b1
А
ℓ1
NB
b2
C
ℓ2
Р
Д
δsВ δsС δsР
4. δА(NB ) = − NB ∙ δsB
2. Отбросим опору В, заменим NВ
3. Возможные перемещения δsС
и δsВ, δsР
Т.к. δφА = δsС /ℓ1, а δφД = δsС/ℓ2,
то δsВ = δφА∙b1= δsС∙b1 /ℓ1 и
δsР = δφД∙b2= δsС∙b2 /ℓ2
и δА(P) = P ∙ δsР
5. Р ∙ δsР − NB ∙ δsB = 0,
b2
6. N B P
b1
1
2
26.
§ 5. Общее уравнение динамикиПрименяя одновременно п-п Даламбера и ПВП, можно
определить общий метод решения задач динамики
Рассмотрим систему материальных точек, на которую
наложены идеальные связи. Если ко всем точкам, кроме
активных сил Fak и сил реакции Nk, добавить силы
инерции Fинk = −mkak, то, по принципу Даламбера,
Fka Nk Fkин 0 rk
A A A 0
a
k
ин
k
r
k
=0
A A A
a
k
k
ин
k
r
k
k
k
0
27. Получим п-п Даламбера-Лагранжа
aин
A
A
k k 0 ( )
k
k
При движении механической системы с идеальными
связями в каждый момент времени сумма
элементарных работ всех приложенных активных сил
и всех сил инерции на любом возможном перемещении
системы равна нулю
a
ин
a
ин
a
ин
F
F
x
F
F
y
F
F
k kx kx k ky ky k kz kz zk 0 ( ')
Общее уравнение динамики в аналитической форме
28. Жа́н Леро́н Д’Аламбе́р (фр. Jean Le Rond d'Alembert; 16 ноября 1717 – 29 октября 1783) – французский философ, механик и математик
29.
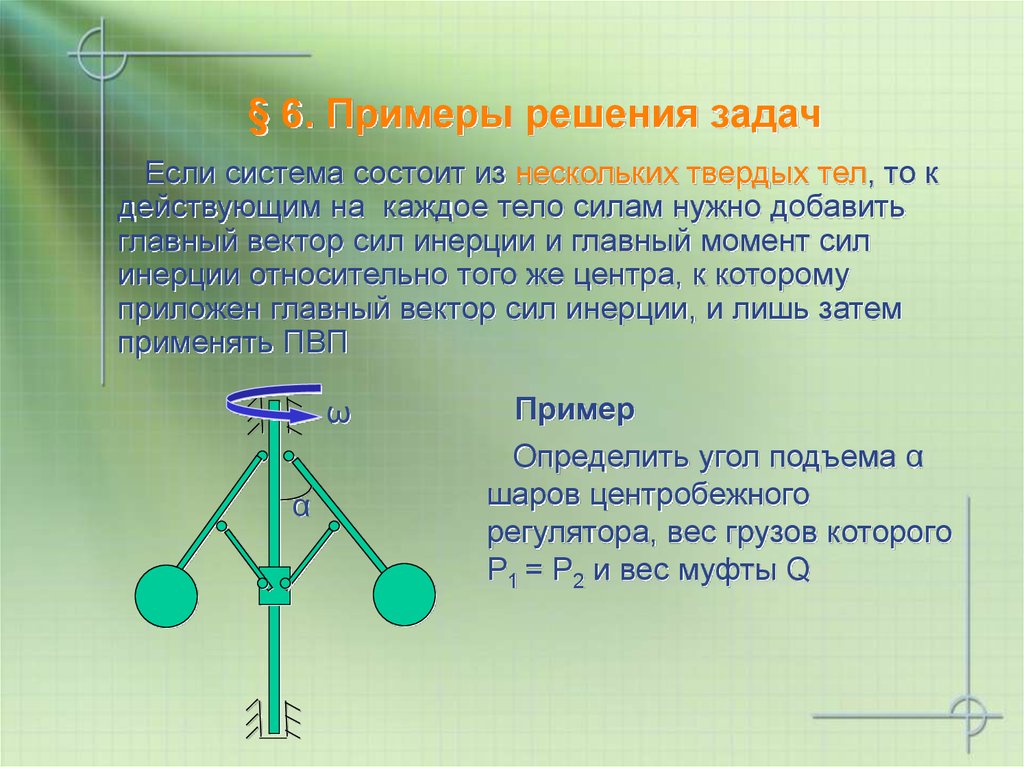
§ 6. Примеры решения задачЕсли система состоит из нескольких твердых тел, то к
действующим на каждое тело силам нужно добавить
главный вектор сил инерции и главный момент сил
инерции относительно того же центра, к которому
приложен главный вектор сил инерции, и лишь затем
применять ПВП
ω
α
Пример
Определить угол подъема α
шаров центробежного
регулятора, вес грузов которого
Р1 = Р2 и вес муфты Q
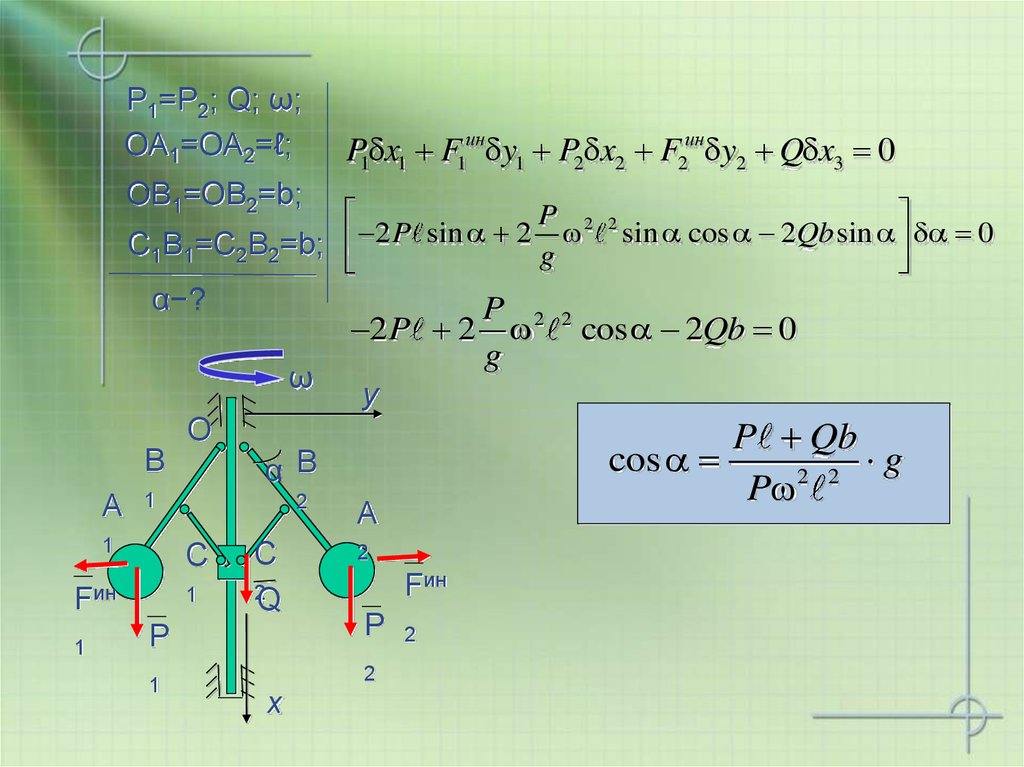
30. Р1=Р2; Q; ω;
ОА1=ОА2=ℓ;При определенном соотношении сил
наступает равновесие
2
при const
ОВ1=ОВ2=b;
V
an
sin
2 2
2
sin
C1В1=C2В2=b;
2 sin
an
sin
α−?
P1 2
ин
ин
F1 F2 sin
ω
g
у
О
P1 x1 F1ин y1 P2 x2 F2ин y2 Q x3 0
В1
В2
α
x1 x2 cos ; y1 y2 sin ;
А1
А2
x3 2 b cos
С1
Fин1
Р1
С2
Q
х
Fин2 Продифференцируем координаты
Р2
x1 x2 sin ;
y1 y2 cos ;
x3 2 b sin
31. Р1=Р2; Q; ω;
ОА1=ОА2=ℓ;P1 x1 F1ин y1 P2 x2 F2ин y2 Q x3 0
ОВ1=ОВ2=b;
P 2
2
P
sin
2
C1В1=C2В2=b;
g
α−?
2 P 2
ω
В
А
2
С
Fин
1
С
2Q
Р
1
х
2
sin cos 2Qb sin 0
cos 2Qb 0
у
P Qb
cos
g
2 2
P
α В
1
1
1
О
P 2
g
2
А
2
Fин
Р
2
2
32.
Пример 2Р1, Р2, Q, М
r1, r2, r, ρ1, ρ2
агр−?
εII
II
Определить ускорение груза подъемника
при постоянном вращающем моменте М
P1 2
M J1 1 1 1
g
P
M 2ин J 2 2 2 22 2
g
М1ин
Q
ин
Fгр aгр
g
I
ин
1
εI
М2ин
агр
Q
Fгрин
M 2ин
1 r2 2
r1
r1
2 1 и 2 1
r2
r2
Т.к. r
1
М
r1
r1
V3 r 2 1 r и a3 1 r
r2
r2
P2 2
r1
Q
r1
ин
2 1
и Fгр 1 r
g
r2
g
r2
=>
33.
Пример 2Определим возможные перемещения:
1 ,
r1
2 1 ,
r2
Р1, Р2, Q, М
r1, r2, r, ρ1, ρ2 Тогда по ПВП
агр−?
εII
δφ2
II
агр δs3
Q
Fгрин
r1
s3 1 r .
r2
Q F3ин s3 M 2ин 2 M M 1ин 1 0
М1ин
Q
r1 r1
Q 1 r r 1
g
r2 r2
I
εI
δφ1 P2 2
r1 r1
2 1
1
=>
g
r2 r2
P1 2
M 1 1 1 0
g
r1
M Qr
r2
r1
1
и a3 1 r
2
2
Q 2 r1
P
r
P
r2
r 2 2 2 2 1 2 1 12
g r2
g
r2
g
М2ин
М






























 physics
physics








