Нахождение квадратных корней

1.

Мы урок сегодня с вами вместе
проведем,
Уравнения порешаем и ответ
найдем,
Урок недлинный, но время
растяжимо,
Оно зависит от того, какого рода
Содержимым вы наполните его.
Что ж, урок начнем сейчас!
Всем удачи, в добрый час!

2.

Hайдите корни уравнения
(x-3)2- 4 = 0
x =1 и x = 5
1)
2)
X2+3 = 8,3
x = … 2,3 ?

3. Цели урока:

Вывод
Графический способ
не является
универсальным :
не всегда позволяет
найти
точные значения
неизвестной

4. Hайдите корни уравнения

Работа с учебником
Пункт 24 стр. 133 – 134
определение 1
определение 2
определение 3
определение 4

5. Вывод

СТОП- МОМЕНТ
a, b и c – некоторые числа, причём а
0
≠
a x2 + b x + c = 0
Первый
коэффициент
Второй
коэффициент
Свободный
член

6. Работа с учебником

1. Выберите из уравнений квадратные
2. Определите коэффициенты a, b, c.
1) 3,5 x 2 6 x 9 0;
4) 4 x 3 5 x 2 0;
2) 6 x x 0;
5) 2,5 x 1 0;
3) 9 x 5 0;
6) 8 x 0;
2
2
3
7) 2 x 2 0.
x
2

7.

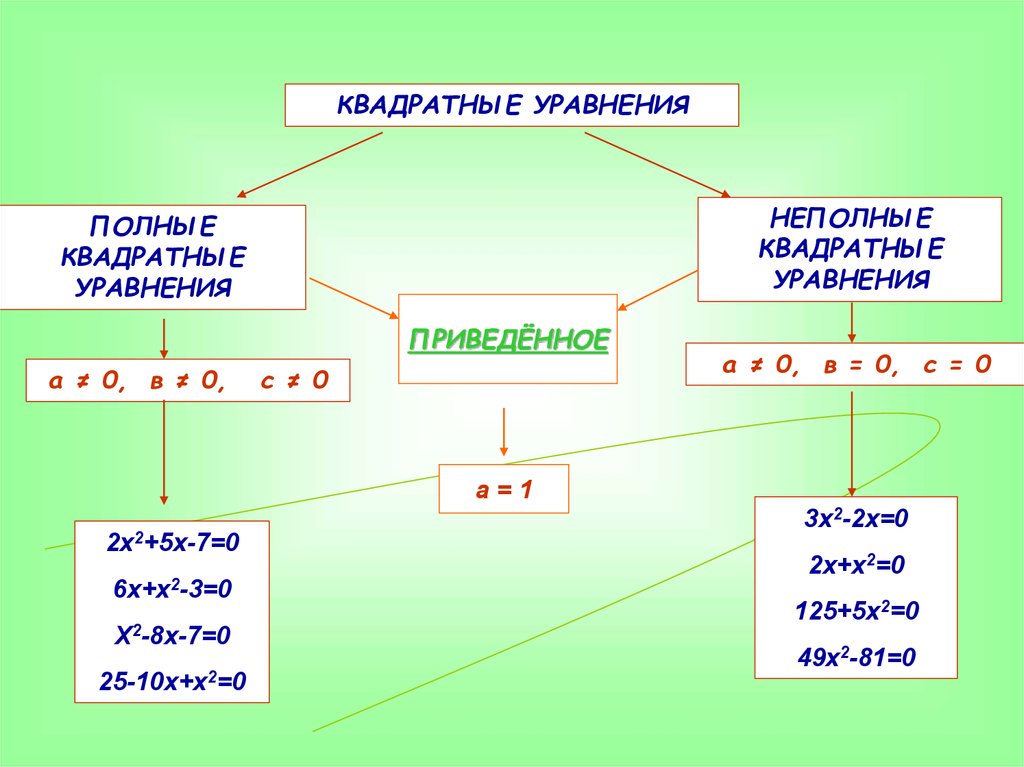
КВАДРАТНЫЕ УРАВНЕНИЯ
НЕПОЛНЫЕ
КВАДРАТНЫЕ
УРАВНЕНИЯ
ПОЛНЫЕ
КВАДРАТНЫЕ
УРАВНЕНИЯ
ПРИВЕДЁННОЕ
а ≠ 0, в ≠ 0,
с ≠ 0
а=1
2х2+5х-7=0
6х+х2-3=0
Х2-8х-7=0
25-10х+х2=0
а ≠ 0, в = 0, с = 0
3х2-2х=0
2х+х2=0
125+5х2=0
49х2-81=0

8. 1. Выберите из уравнений квадратные 2. Определите коэффициенты a, b, c.

Проверь себя
Уравнение
х 2 5х 3 0
6х 2 5 0
2х 2 4х 0
5х 7 х 2 2 0
2х 2 0
Полное
Неполное
Приведен
ное
Неприведенное

9.

Здесь вы видите уравнения, определённые по
какому-то признаку. Как вы думаете, какое из
уравнений этой группы является лишним?
1. x2 – 9x = 0,
2. 4x2 – х – 3 = 0,
3. 16 – x2 = 0,
4. 4x2 = 0.
1. 5x2 – 2x – 3 = 0,
2. x2 + 2x – 35 = 0,
3. 2x2 + 9x – 11 = 0,
4. -4x2 – 6x + 5 = 0.
1. x2 – 5x + 1 = 0,
2. x2 + 3x – 5 = 0,
3. 2x2 – 7x – 4 = 0,
4. x2 + 2x = 1 = 0.

10. Проверь себя

«Ушки
на макушке»

11.

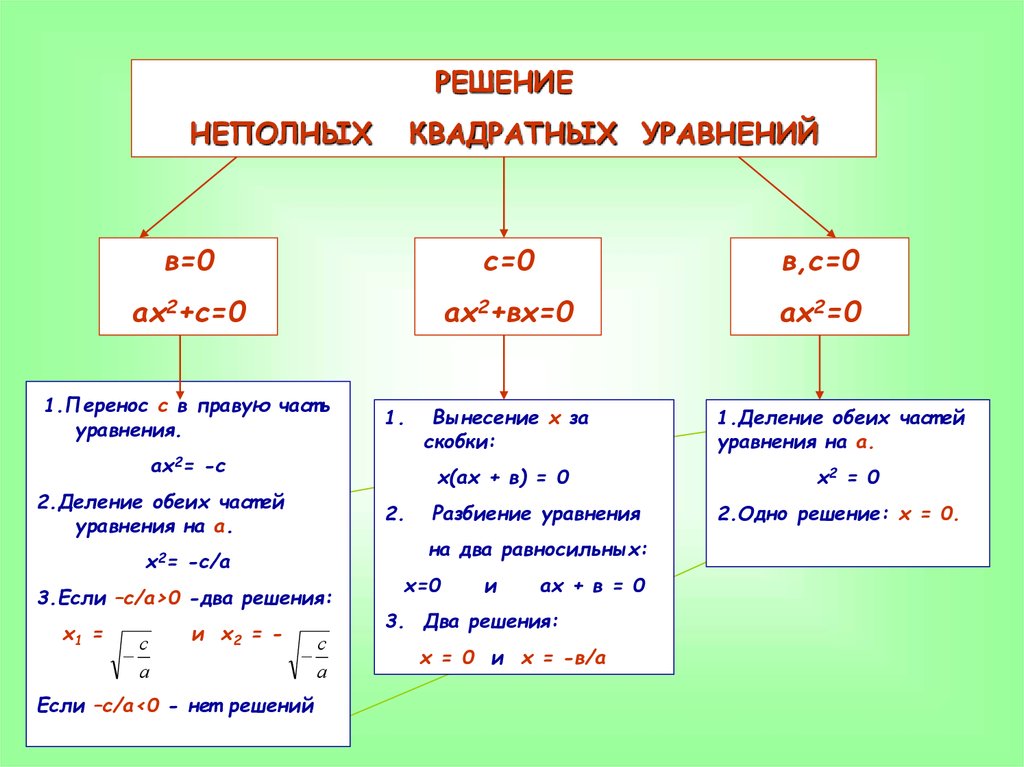
РЕШЕНИЕ
НЕПОЛНЫХ
КВАДРАТНЫХ УРАВНЕНИЙ
в=0
с=0
в,с=0
ах2+с=0
ах2+вх=0
ах2=0
1.Перенос с в правую част ь
уравнения.
1.
ах2= -с
х(ах + в) = 0
2.Деление обеих част ей
уравнения на а.
2.
3.Если –с/а>0 -два решения:
с
а
и х2 = -
Разбиение уравнения
на два равносильных:
х2= -с/а
х1 =
Вынесение х за
скобки:
Если –с/а<0 - нет решений
с
а
х=0
и
ах + в = 0
3. Два решения:
х = 0 и х = -в/а
1.Деление обеих част ей
уравнения на а.
х2 = 0
2.Одно решение: х = 0.

12.

Решение неполных квадратных
уравнений (с = 0)
5х2 – 12х = 0
х(5х – 12) = 0
х1 = 0 или
Ответ: 0; 2,5
5х – 12 = 0,
5х = 12,
х2 = 2,5.

13.

Решение неполных квадратных уравнений
b=0
9х2 – 16 = 0,
9х2 = 16,
х2 = 16
9
х = 16
9
х1 = 4 х2 = 4
3
3
1 1
Ответ: 1 ; 1
3 3
3х2 + 27 = 0,
3х2 = - 27,
х2 = - 9.
т.к. - 9 < 0, то уравнение
корней не имеет.
Ответ: корней нет

14.

Самостоятельная работа
Вариант 1
Вариант 2
а
в
16
17
16
18
20
17
18
20

15.

Задача знаменитого индийского
математика Бхаскары
Обезьянок резвых стая
Всласть поевши, развлекаясь,
Их в квадрате часть восьмая
На поляне забавлялась.
А двенадцать по лианам
Стали прыгать, повисая.
Сколько было обезьянок
Ты скажи мне в этой стае?

16. Самостоятельная работа

Уравнение к задаче
Бхаскары:
2
x
+ 12 = х
8

17. Историческая справка.

Задача по геометрии, приводящая
к квадратному уравнению
Дано: АВС- прямоугольный равнобедренный,
АВ=ВС , АС = 8
Найти: АВ
Решение:
• Пусть х – длина катета.
• По теореме Пифагора:
AC AB BC
2
2x
2
2
8
2
A
х
2
B
C

18. Задача знаменитого индийского математика Бхаскары

Домашняя работа: