Игры (геометрия). Статические игры

1. Игры (геометрия) Статические игры

2.

Геометрический способ решения игры(2x2)
V (a11 a21) p1 a21
V’
1 уравнение
a p a (1 p ) V
21
1
11 1
a p a (1 p ) V
22
1
12 1
V
2 уравнение
1
P1
P
Варианты решений:
V’
V’
V’
V’
V
V
P
P
V’
V
P
V’
V’
V
V
V
P
P
P
V
P

3.

Геометрическое решение игры (2xN) и (Mx2)
0 0 q3 q4
2
4
2 3 1
3 2
6
p1
p2 1 p1
2 p 4(1 p ) V
1
1
2 p1 3(1 p1 ) V
3 p1 2(1 p1 ) V
p 6(1 p ) V
1
1
p1 2 7 p1 6
8 p1 4
1
1
p1* , p2*
2
2
V 2,5
2 p 4 V
1
p 3 V
1
p1 2 V
7 p 6 V
1
3q3 q4 2,5
3q3 1 q3 2,5
4q3 3,5
7
1
q3* , q*4
8
8

4.

Приведение игры к ЗЛП
m
aij pi V
i 1
m
pi 1,
i 1
p 0 (i 1,m)
i
p
x i
i V
m
aij xi 1
i 1
(i 1,m)
n
aij q j V
j 1
n
q j 1, q j 0 ( j 1,n)
j 1
q
y j
j V
n
aij y j 1
j 1
( j 1,n)
1
x x x min
1 2
m V
1
y y y max
1 2
m V
x 0 (i 1,m)
i
y 0 ( j 1,n)
j

5.

Статические игры (игры с “природой”)
П ......................П поведение природы
1
n
A a11........................a1n
1
A a ........................a
2 21
2n
..................................
A a ..........................a
m m1
mn
q ...........................q
1
n
Существуют два класса игр с природой:
1. Первый класс, когда к каждому состоянию природы можно
приписать некоторую вероятность.
• Второй класс, когда к каждому состоянию природы не
можем приписать некоторую вероятность.

6.

Принципы и критерии для выбора решения
1. Критерий Байеса
Оптимальной стратегией будет стратегия, в которой достигается
max a
i
n
a a q
i
ij j
j 1
2. Принцип недостаточного основания Лапласа
Если мы не знаем вероятности, то положим состояние природы
1
равновероятными:
q
j n
3. Максиминный критерий Вальда
min aij .
Оптимальна та стратегия, в которой лежит элемент max
j
i
Это пессимистический критерий (рассчитан на самый хороший
вариант в самом плохом случае).

7.

4. Критерий минимального риска Сэвиджа
r a риск игрока А
ij
j ij
β max a
j
ij
(r )
матрица риска
ij mxn
Риск – плата за отсутствие информации.
Оптимальна та стратегия, в которой лежит минимальный из
максимальных рисков:
w min max r .
ij
i
j

8.

5. Критерий оптимизма – пессимизма Гурвица
max[ min (a ) (1 ) max(a )], где 0 1
ij
ij
j
i
j
коэффициент оптимизма
1 крайний пессимизм критерий Вальда
0 крайний оптимизм
0,6

9.

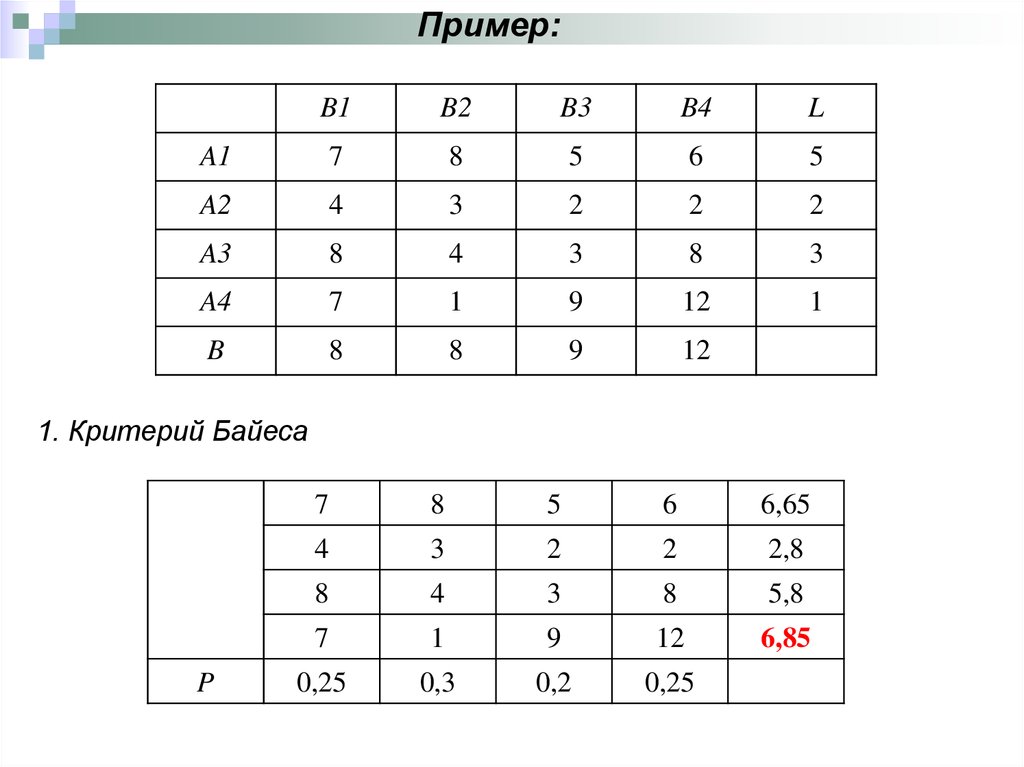
Пример:
B1
B2
B3
B4
L
A1
7
8
5
6
5
A2
4
3
2
2
2
A3
8
4
3
8
3
A4
7
1
9
12
1
B
8
8
9
12
1. Критерий Байеса
P
7
8
5
6
6,65
4
3
2
2
2,8
8
4
3
8
5,8
7
1
9
12
6,85
0,25
0,3
0,2
0,25

10.

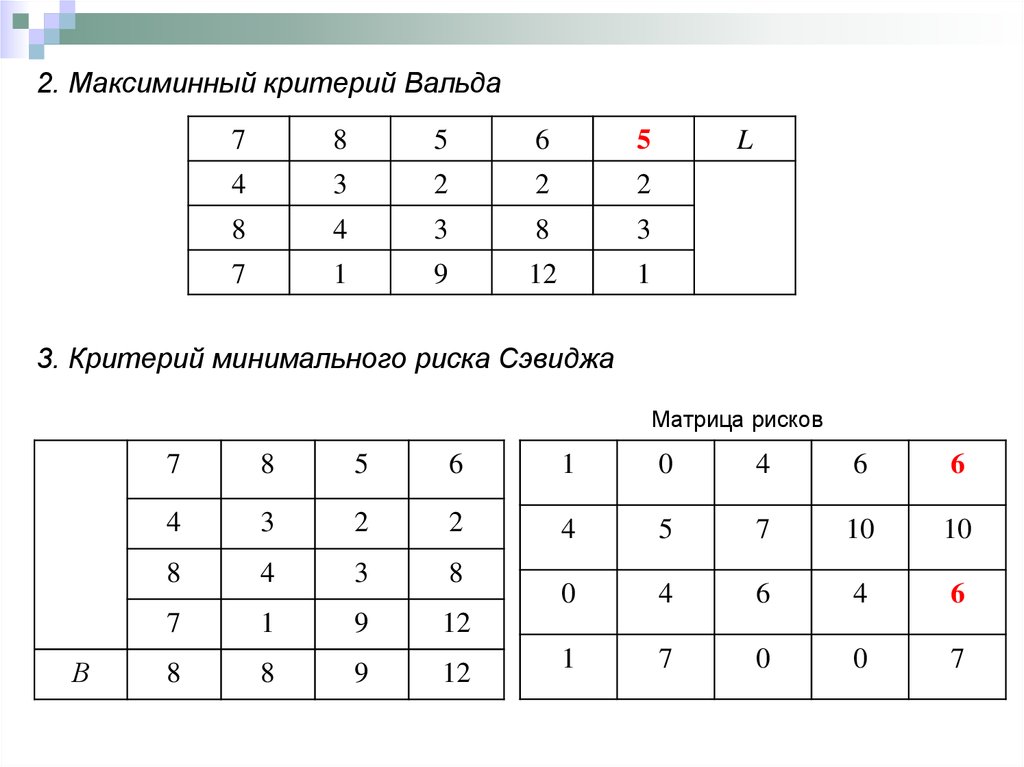
2. Максиминный критерий Вальда
7
8
5
6
5
4
3
2
2
2
8
4
3
8
3
7
1
9
12
1
L
3. Критерий минимального риска Сэвиджа
Матрица рисков
В
7
8
5
6
1
0
4
6
6
4
3
2
2
4
5
7
10
10
8
4
3
8
0
4
6
4
6
7
1
9
12
8
8
9
12
1
7
0
0
7

11.

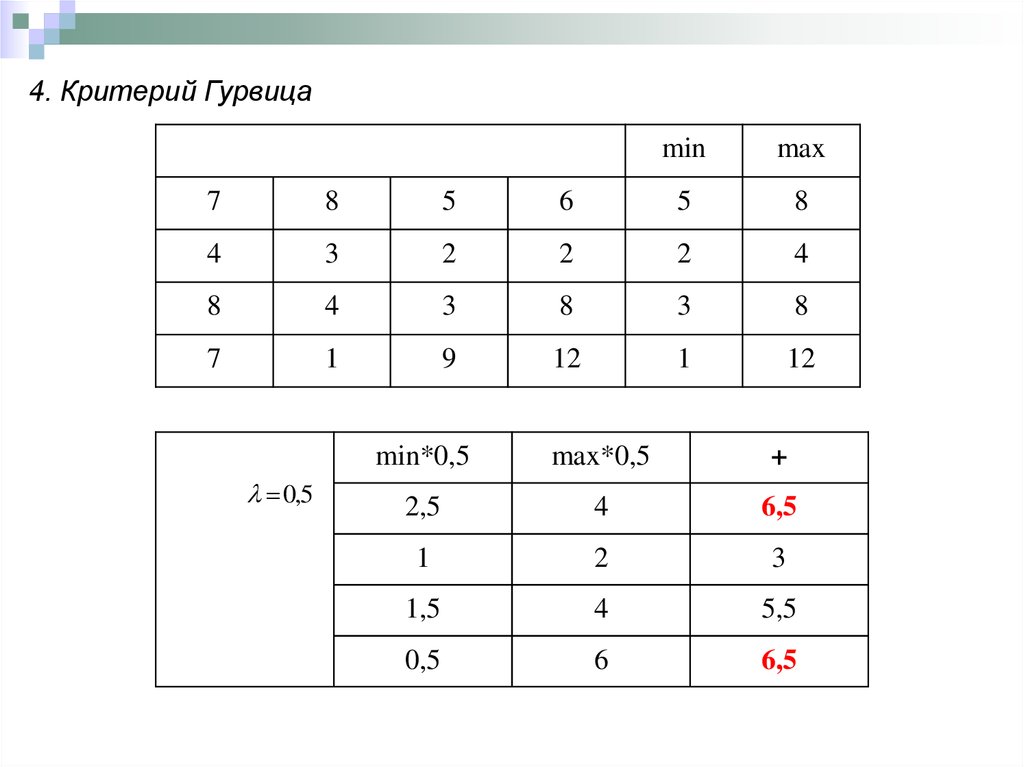
4. Критерий Гурвица
min
max
7
8
5
6
5
8
4
3
2
2
2
4
8
4
3
8
3
8
7
1
9
12
1
12
0,5
min*0,5
max*0,5
+
2,5
4
6,5
1
2
3
1,5
4
5,5
0,5
6
6,5