Применение формулы Ньютона-Лейбница

1.

Применение формулы Ньютона-Лейбница
бывает
сложным,
так
как
бывает
трудно
найти
первообразную функции.
Поэтому
используются
численные
методы,
позволяющие
найти
приближенное
значение
определенного интеграла с заданной точностью.

2.

Основной принцип построения формул
приближенного вычисления определенного
интеграла состоит в замене частичных
криволинейных трапеций, образующихся при
разбиении отрезка интегрирования, на более
простые фигуры.

3.

Пусть на отрезке [a,b] задана
неотрицательная функция y=f(x).
Тогда интеграл
непрерывная
b
f ( x)dx
a
равен площади под кривой y=f(x) на отрезке [a,b].
Мы получим приближенное значение этого интеграла,
если вместо площади под кривой возьмем
площадь под ломаной, подходящей достаточно
близко к этой кривой.

4.

Для этого разобьем [a,b] на n равных частей длиной
b a
h
n
и на каждом из отрезков разбиения
[ xi 1 , xi ]
где
i 1,2,..., n
заменим участок кривой y=f(x) хордой, стягивающей
концевые точки.

5.

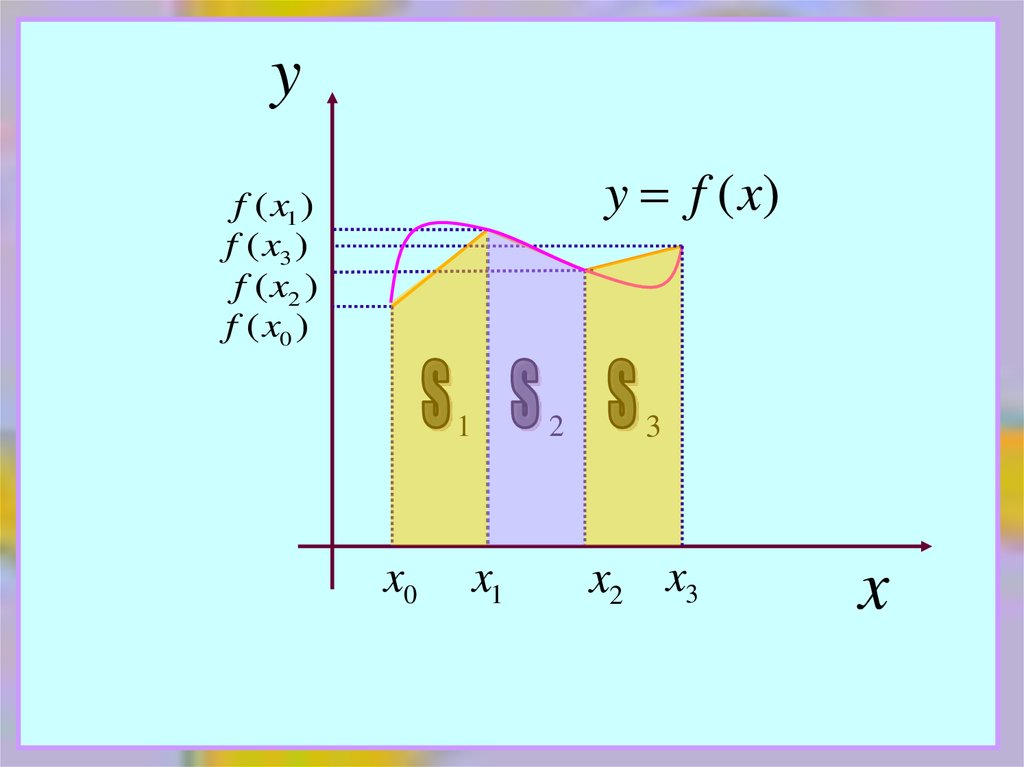
y
y f (x)
f ( x1 )
f ( x3 )
f ( x2 )
f ( x0 )
1
x0
2
x1
3
x2 x3
x

6.

b
f ( x)dx S
1
S2 ... Sn
a
где каждое слагаемое представляет собой площадь
трапеции:
f ( x0 ) f ( x1 )
S1
h
2
f ( x1 ) f ( x2 )
S2
h
2
f ( xn 1 ) f ( xn )
Sn
h
2
...

7.

Тогда
b
a
f ( x0 ) f ( x1 )
f ( x1 ) f ( x2 )
f ( x)dx
h
h
2
2
f ( xn 1 ) f ( xn )
...
h
2
f ( xn )
f ( x0 ) f ( x1 ) f ( x1 ) f ( x2 )
h
...
2
2
2
2
2
Все слагаемые, кроме первого и последнего
повторяются дважды.

8.

Учитывая, что
b
a
b a
h
получаем
n
b a f ( x0 ) f ( xn )
f ( x)dx
f ( x1 ) f ( x2 ) ...
n
2

9.

Обозначим выражение в правой части как S(n). Тогда
абсолютная погрешность от применения формулы
трапеций составит
b
f ( x)dx S (n)
a
Пусть М2 - максимальное значение модуля второй
производной подынтегральной функции на [a,b]:
M 2 max f ( x)
x a ,b

10.

Доказано, что
(b a)
M2
2
12n
3

11.

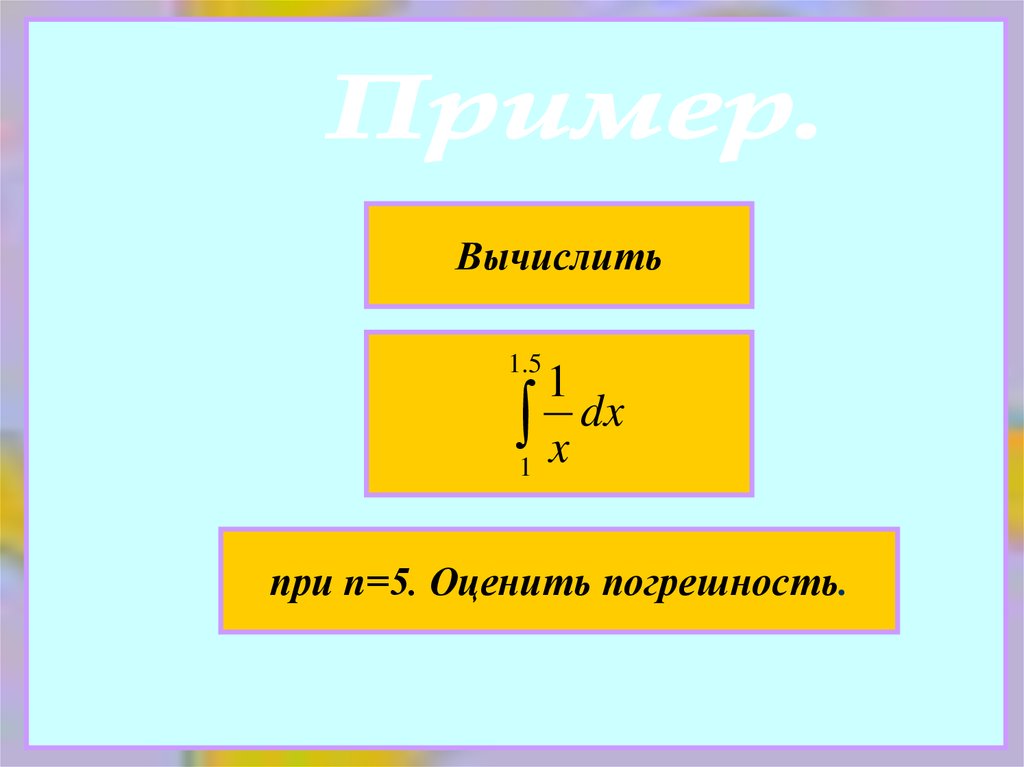
Вычислить
1 .5
1
1 x dx
при n=5. Оценить погрешность.

12.

n=5, следовательно длина отрезков разбиения
b a 1.5 1
h
0.1
n
5
x0 a 1,
x3 1.3,
x1 1.1,
x4 1.4,
x2 1.2,
x5 b 1.5
1
1
1 1
1
1
1
1 x dx 0.1 2 1 1.5 1.1 1.2 1.3 1.4 0.4059
1.5

13.

Найдем погрешность:
1
f ( x) 2
x
2
f ( x ) 3
x
Эта функция монотонно убывает на данном отрезке,
следовательно она достигает своего максимального
значения в крайней левой точке при х=1.
2
M 2 f (1) 3 2
1
0.53
3
2 0.84 10
2
12 5

14.

В основе формулы Симпсона лежит замена двух
соседних частичных криволинейных трапеций,
ограниченных
сверху
функцией
y=f(x)
на
криволинейную трапецию, ограниченную сверху
параболой вида
y Ax Bx C
2
Поэтому формулу Симпсона
формулой парабол.
часто
называют

15.

Разобьем [a,b] на 2n равных частей. Тогда кривая
разобьется прямыми
x xi
на 2n частей точками М0, М1,...М2n.
Через каждую тройку точек М0, М1, М2… проведем
параболу. Коэффициенты А,В,С находятся из
условия ее прохождения через тройку точек.
Таким
образом,
криволинейная
трапеция,
ограниченная сверху функцией y=f(x), заменяется
составной фигурой, ограниченной сверху n
параболами.

16.

y
M2
M3
M1
x0
x1
x2
x3
y f (x)
x

17.

b
a
b a n 1
f ( x)dx
( f ( x2i ) 4 f ( x2i 1 ) f ( x2i 2 ))
6n i 0

18.

Пусть М4 - максимальное значение модуля четвертой
производной подынтегральной функции на [a,b]:
M 4 max f
( 4)
x a ,b
Тогда погрешность вычислений
Симпсона оценивается как:
( x)
по
(b a)
M4
4
2880n
5
формуле

19.

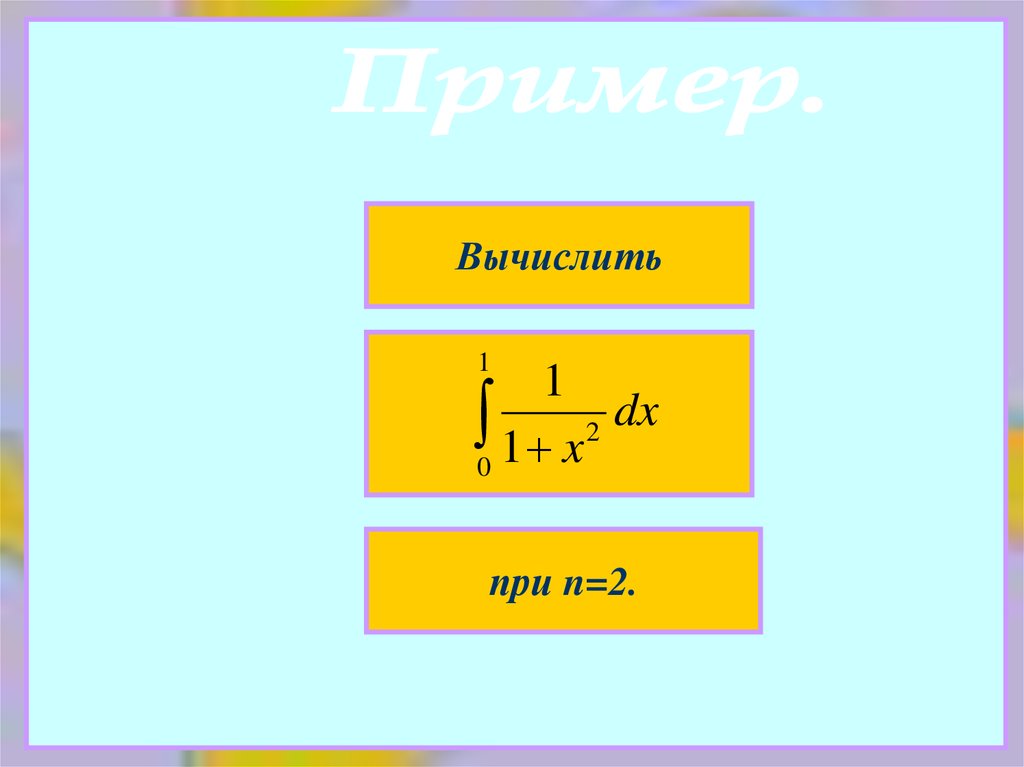
Вычислить
1
1
0 1 x 2 dx
при n=2.

20.

n=2, следовательно полное число узлов равно 5.
i
0
1
2
3
4
xi
0
0.25
0.5
0.75
1
yi
1
0.941176
0.8
0.64
0.5
Тогда
1
1
0 1 x 2 dx
1
1 0.5 2 0.8 4 (0.941176 0.64) 0.785392
12