Семiнар практикум по підготовці питань до екзамену з дисципліни методика формування елементарних математичних уявлень

1.

по підготовці питань до екзамену
з дисципліни
методика формування елементарних
математичних уявлень
Викладач Камінська О. А.

2.

Перелік питань:
1. Розкрийте суть теоретико-множинного підходу до
навчання лічби. Складіть фрагмент заняття з ФЕМУ
2. Послідовність формування знань про геометричні
фігури. Обгрунтуйте особливості ознайомлення з ГФ в
кожній віковій групі
3. Логіко-математичні ігри
4. Охарактеризуйте послідовність навчання дітей
вимірювання довжини умовною міркою. Розкрийте
важливість використання дітьми дошкільного віку
вимірювання в різних видах діяльності.
5. Методика формування часових уявлень у дітей
дошкільного віку

3.

Алгоритм відповіді
студента:
1. Актуальність даного питання
2. Психолого-педагогічні обґрунтування
3. Внесок видатних науковців у розвиток
даного питання
4. Методика та прийоми навчання
дошкільників
5. Розробка фрагментів логікоматематичних ігор з вказаною метою і
наочністю
6. Проведення дидактичної гри або
фрагменту

4.

5.

Ганна Михалівна
Лєушина
розробила
теоретико –
множинний підхід
до навчання дітей
лічби. Це означає,
що при навчанні
лічби ми
використовуємо
дві множини
предметів (
ялинки та
зайчики) . Вона
розробила
теоретико –
множинний підхід
у 1956 році,але він
актуальний і до
сьогодні.

6.

Теоретико-множинний підхід став
надзвичайно важливою розробкою у
роботі з методики ФЕМУ. За його
допомогою вихователь формує поняття
“багато”, “порівну”, “більше”, “менше”,
“наскільки більше чи менше”. Крім того,
множина дає можливість застосувати у
практиці знання дітей про цифри і лічбу,
вони вчаться рахувати предмети і
співвідносити їх кількість.
При використанні теоретико-множинного
підходу варто також сказати про

7.

8.

9.

10.

11.

12.

13.

14.

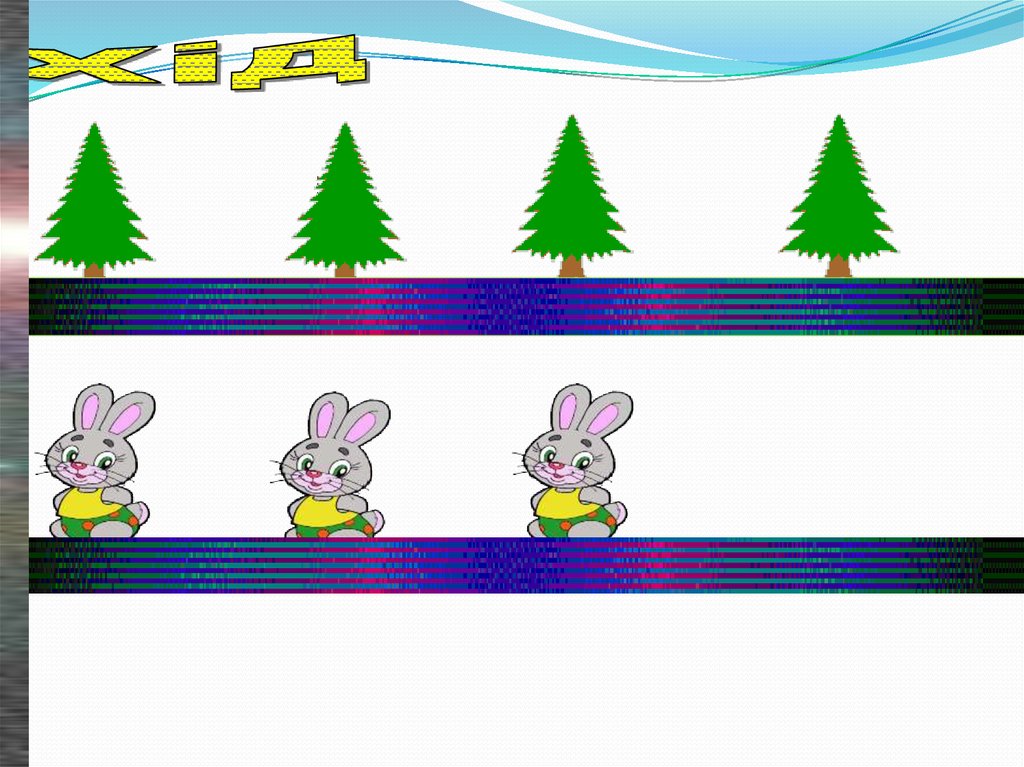
- Діти в лісі виросла поляна,а на ній багато
ялинок,давайте перелічимо,скільки
їх?(виставляємо на верхню смужку 4
ялинки і при цьому перелічуємо)
-під кожну ялинку прискакав
зайчик,скільки їх?(перелічуємо
- А скільки ялинок?(порівну
-А скільки зайчиків ?( порівну
-- А ось і виросло ще одне дерево,і це
ялинка,скільки ялинок?(більше
-- А скільки зайчиків?(менше
-- А на скільки більше ялинок?( на одну
-- А на скільки менше зайчиків? (на одну
-- А що потрібно зробити,щоб і зайчиків і
ялинок стало порівну?
- А ось і прискакав ще один зайчик,то
скільки їх?(порівну

15. Послідовність формування знань про геометричні фігури. Обгрунтуйте особливості ознайомлення з ГФ в кожній віковій групі

16. Сенсорний розвиток

Сенсорний (лат. sensorium — орган чуттів)
розвиток дитини — розвиток її відчуттів і
сприймання, формування уявлень про
властивості предметів (форму, колір, розмір,
положення у просторі тощо).
У ранньому віці на сенсорній основі базуються
всі лінії розвитку дитини.

17.

Завдання вихователя не просто дати дітям знання,
а й навчити малюків:
міркувати;
грамотно обґрунтовувати свою позицію;
самостійно приймати рішення;
не уникати завдань із багатьма
варіантами розв’язання.
Одним із засобів введення
дітей у світ
логіко-математичних
уявлень є дидактичні ігри
та інтелектуальні ігри.

18.

Знайомство з геометричними фігурами
Знайомство з властивостями геометричних фігур (кольором, формою,
розміром, розташуванням на площині тощо) у порівнянні з різними
предметами навколишнього світу допомагає глибше пізнати оточуюче
середовище, встановлювати зв’язки між ними. Порівнюючи істотні
ознаки та об’єднуючи предмети в групи чи класи, діти оволодівають
способами логічного мислення.

19.

Ознайомлення дітей молодшого дошкільного віку з геометричними
фігурами.
Перші відомості про геометричні фігури діти отримують в іграх. На початку навчального року в
групу вносять набір куль, будівельні матеріали, геометричну мозаїку і ін. Граючи з дітьми, педагог
з самого початку вживає правильні назви геометричних фігур, але не прагне до того, щоб діти їх
запам'ятовували.
У цей період важливо розвивати сприйняття дітей, накопичити у них уявлення про різноманітні
форми. У групах раннього віку дітей вчили розрізняти кулю і куб. Однак деякі діти приходять у
другу молодшу групу вперше, тому доцільно почати роботу зі знайомства з цими фігурами.
Займаючись з підгрупою малюків, педагог показує і називає кулю і виробляє різноманітні дії з
нею: катає її по столу, між долонями, перекочує з руки в руку. В процесі дій він промовляє: "Куля
котиться. Я перекотиполе куля з руки в руку".
Аналогічним чином дітей знайомлять з кубом. Але так як у них вже є досвід обстеження форми
предметів, то їм відразу показують моделі кубів різних розмірів. Педагог спочатку показує і
називає куб. А потім, пред'являючи 2 куба контрастних розмірів, запитує: "Що це? Якого кольору
куби? Який куб більше (менше)?" Діти обмацують куб, обводять пальчиком його грані,
обхоплюють руками, пробують котити і переконуються в його стійкості. Вони ставлять маленький
куб на великий, вибирають куби з інших предметів, роблять з них найпростіші споруди і т. п.
Суттєве значення надається навчанню малюків прийомам обведення контурів моделей
геометричних фігур і простежування поглядом за рухом руки. Вихователь показує фігуру, називає
її, просить дітей показати таку ж, а далі неодноразово обводить контур фігури вказівним пальцем,
залучаючи дітей до спільної дії "в повітрі". Рух пальця по контуру завершується проведенням
рукою по всій поверхні фігури. Діти стежать за рухом руки педагога, а після самі обводять модель
фігури і називають її.

20.

Молодший дошкільний вік
Геометричні фігури діти візуально
розпізнають, хоча не знають їх назв. Вони можуть
показати, що сонечко,
бублик, кермо, колесо – круглі,
а стіл – квадратний, не називаючи геометричні
фігури круг, квадрат, куля, куб.
ГФ Вчити розрізняти і
називати гф:площинні – круг,
квадрат, трикутник та
об’ємні – куля,куб.
Навчати їх обстежувати
дотиково-руховим і зоровим способами.
Вчити впізнавати і називати гф та форми в
навколишніх предметах.

21. Дидактичні ігри

Дидактичні ігри - один із універсальних
способів розвитку, виховання і навчання дітей.
Вони приносять в життя дитини радість,
інтерес, упевненість у собі і своїх можливостях.
Головна особливість дидактичних ігор полягає в
тому, що завдання дітям пропонуються в ігровій
формі.

22. Кубики-вкладиши

Цікавими для малят є ігри з кубиками-вкладишами, які
сприяють розвиткові логічного мислення,уяві, дрібній
моториці рук.
Такі іграшки допомагають малюкові познайомитися із
геометричними фігурами, а також пізнавати їх у довколишніх
предметах.

23.

Діти залюбки граються такими іграми.
Сприяє розвитку логічного мислення.

24.

Ознайомлення дітей середнього дошкільного віку з геометричними фігурами.
Дітей середнього дошкільного віку потрібно ознайомити з трикутником, прямокутником та
циліндром.
З новими геометричними фігурами діти знайомляться на основі їх порівняння з уже знайомими.
Так, ознайомити з трикутником можна на основі закріплення знань про квадрат і, порівнюючи їх
один з одним. Покажіть дитині квадрат, вирізаний з паперу. На ваше запитання: «Що це таке?»дитина відповість, що це квадрат. А тепер зігніть квадрат по діагоналі і розріжте його - вийде два
трикутника. Один трикутник залиште у себе, а інший - віддайте дитині. Ви демонструєте перед
дитиною нову фігуру і називаєте її: «Це трикутник. У цієї фігури є кути і сторони». Запропонуйте
дитині вказівним пальцем правої руки обвести по контуру фігуру, доторкнутися до кутів. Зробіть
це разом з нею. Ці дії сприятимуть більш глибокому і активному обстеженню фігури. Кілька разів
запитайте у дитини, як називається фігура. Отримані знання потрібно закріпити в різних формах
дитячої діяльності: ігровій, побутовій, конструктивній. Можна запропонувати дитині гру «Знайди
предмет трикутної форми». Дитина в навколишньому середовищі знаходить і називає предмети:
підставка для сковороди, формочки для печива тощо.
Ознайомлення дітей з прямокутником можливе також на основі порівняння його з квадратом.
При цьому слід розділити квадрат на дві частини. Зверніть увагу дитини на те, що вийшли дві нові
фігури, у яких, як і у квадрата, є сторони і кути. Ці фігури називаються прямокутниками.
«Порахуй, скільки сторін у прямокутника. А скільки у нього кутів? Сторін і кутів порівну, їх по
чотири. Порівняй сторони прямокутника між собою - вони рівні попарно). А що ми говорили про
сторони квадрата? (Вони рівні між собою). Обведи пальчиком сторони прямокутника. Покажи
пальчиком кути прямокутника. Тепер знайдемо в кімнаті предмети, за формою схожі на
прямокутник». Дитина називає картину, раму вікна, двері тощо.
Знайомство з циліндром можна організувати, порівнюючи його з кубом. Дитина розглядає куб,
погладжує окремі його сторони-грані. Потім дорослий звертає його увагу на нову фігуру, яка
називається циліндром. У цієї фігури є верхня і нижня основи, а також бічна поверхня. У циліндра
немає кутів, його можна покотити, можна поставити на основу, і він буде стійко стояти. Дитина
виділяє циліндричну форму у склянки, палиці, олівця і т. д.

25.

Середній дошкільний вік
Дитина розрізняє і називає відомі їй гф, їх характерні
ознаки; відшуку у навколишніх предметах подібність за
формою зі знайомими гф.
ГФ Закріплювати назви гф: круг, квадрат, трикутник,
прямокутник та просторових геометричних форм:
куля,куб,знаходячи їх у предметах навколишнього
середовища. Вчити визначати складові гф та просторових
геометричних форм за допомогою зорового і тактильного
аналізаторів. Давати уявлення, що гф можуть бути різної
величини,вправляти їх у визначенні їх величин.
Ознайомлювати з гф «прямокутник» та просторовою
геометричною формою «Циліндр».Пояснювати,у чому
схожість та відмінність прямокутника і квадрата.

26. Дидактична гра “ Чарівні фігурки”

Ознайомлюючись з геометричними фігурами,діти порівнюють
їх,сортують,досліджують ознаки. Можна запропонувати
вихованцям скласти з геометричних фігур будиночок,машину
тощо.

27.

У процесі гри діти закріплюють виділені ознаки,
вправляються в описі фігур(величина,колір, форма)

28.

“Яка геометрична фігура”
Логічні завдання на прикладі “Яка геометрична фігура” спонукають
дитину уважно складати геометричні фігури в отвори .

29. Дидактична гра «Підбери фігуру»

Дидактична гра
«Підбери фігуру»
«Кишеньки з секретом
Мета: ця гра допоможе запам'ятати назви геометричних фігур, а також
розвинути пам'ять добирати геометричну фігуру до її зображення на
малюнку;уміти
за контуром визначати зображені фігури, сприяти
розвитку логічного мислення, уміння узагальнювати,розмірковувати.

30.

«Кишеньки з секретом»

31. Дидактична гра «Відгадайте казку»

32.

Старший дошкільний вік
Дошкільники добре засвоюють матеріал про гф, вміють застосовувати
набути знання на практиці, тобто знайти у побуті предмет відповідної
форми
(круглої,прямокутної тощо).
Вони активно шукають відмінне
і подібне у гф,групують їх.
Важчим є завдання є назвати
просторові геометричні форми:куля,циліндр.
ГФ Вправляти у розрізненні та називанні
гф:квадрат,круг,трикутник,прямокутник.
Ознайомлювати з овалом і ромбом. Вправляти у з
ображенні гф за допомогою паличок, малювати
олівцем,пензликом,крейдою. Закріплювати
вміння розрізняти і називати просторові
та
геомпетричні форми:
куля,куб,циліндр,конус;
називати структурні елементи:
вершина,сторона,кут.

33.

Гра «Якої фігури не стало».
На фланелеграфі викладаються
геометричні фігури в певному порядку.
Діти називають їх і запам’ятовують
розташування. За сигналом вихователя
діти заплющують очі, вихователь
забирає одну або дві фігури.
Розплющивши очі, діти мають
визначити, яких фігур не вистачає. Гра
повторюється два-три рази.

34.

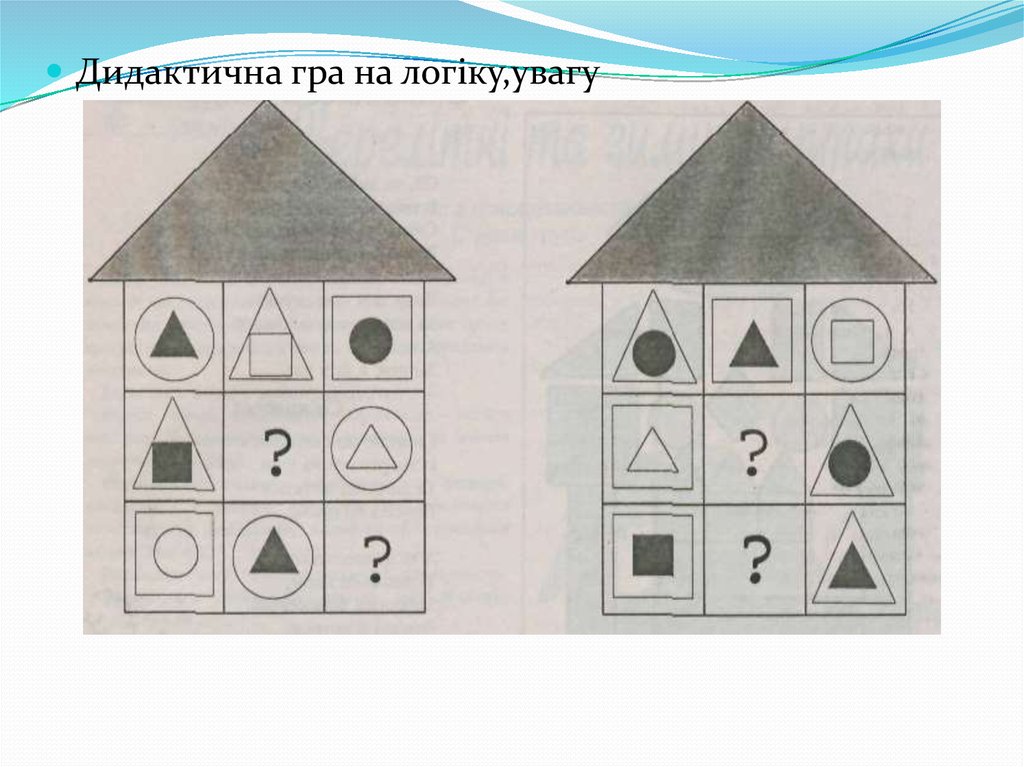
Дидактична гра на логіку,увагу

35.

36.

Які красиві квіти виросли на галявині! Розкажи, якої
форми в них пелюстки.
24.07.2017
36

37.

Які цікаві рибки! На які фігури вони схожі?
24.07.2017
37

38.

З яких фігур миші побудували казкове місто?
24.07.2017
38

39.

З яких фігур складена ця картинка?
24.07.2017
39

40.

Послідовність ознайомлення дошкільників з формою предметів
1)Демонстранція і називання
2)Обстеження шляхом практичних дій
3)Порівняння ГФ за формою,кольором величиною,прийомами
накладання і прикладання
4)Серіація,класифікація ГФ
5)Визначення форми оточуючих предметів
6)Аналіз геометричної фігури
7)застосування знань про ГФ на інших заняттях та у повсякденному
житті
8)Зображення ГФ, складання ГФ шляхом конструювання з двох інших
9)Розвиток термінологічного словника
10)Використання методичних прийомів навчання:
-дид\ігор,дид\вправ
-ігрових прийомів навчання
-цікавої наочності по ознайомленню з ГФ
-худ слово про ГФ
-обовязкові практичні дії з ГФ
11)вимірювання умовною міркою
12)моделювання казок за допомогою ГФ
13)Зорові диктанти з ГФ
40

41. Логіко-математичні ігри

Підготувала студентка 4-А курсу
Бердичівського педагогічного
коледжу
Хворостяна Ольга Юріївна

42. Логіко-математичні ігри-це ігри,в яких змодельовані математичні відносини,закономірності,що припускають виконання логічних операцій і ді

Логіко-математичні ігри-це ігри,в яких змодельовані
математичні відносини,закономірності,що припускають
виконання логічних операцій і дій.

43. «Палички Кюїзенера» Палички Кюїзенера являють собою кольорові пластмасові брусочки (призми) різної довжини. Плоский варіант паличок – см

«Палички Кюїзенера»
Палички Кюїзенера являють собою кольорові пластмасові
брусочки (призми) різної довжини. Плоский варіант паличок –
смужки – можна виготовити власноруч з двохстороннього
картону.
Розмір,
см.
Колір
Умовне
Число
Колір
Кількість
позначення
1
Білий
25
2
Рожевий
20
3
Блакитний
16
4
Червоний
12
2Х2
Біла
1
2Х4
Рожева
2
2Х6
Блакитна
3
2Х8
Червона
4
2Х10
Жовта
5
5
Жовтий
10
2Х12
Фіолетова
6
6
Фіолетовий
9
2Х14
Чорна
7
7
Чорний
8
2Х16
2Х18
Бордова
Синя
8
9
8
бордовий
7
9
Синій
5
2Х20
Оранжева
10
10
оранжевий
4

44. Використання чисел в кольорі дозволяє розвинути у дошкільнят уявлення про число на основі рахунку та вимірювання. Виділення кольору та до

Використання чисел в кольорі дозволяє розвинути у дошкільнят уявлення про число на
основі рахунку та вимірювання. Виділення кольору та довжини паличок допоможе
дошкільникам засвоїти ключові для їх віку засоби пізнання – сенсорні еталони і такі
способи пізнання, як порівняння, зіставлення предметів за деякими ознаками.
Від елементарної гри з кольоровими паличками діти поступово просуваються до
поняття просторово-кількісних характеристик, які засвоюються в спільній діяльності
дитини та дорослого. Важко не обмежувати показом готових будов. Необхідно дати
можливість обирати дії дитині самій, тоді гра стане радісним відкриттям нового. Діти
швидко вчаться переводити гру фарб в числові відношення. Перш ніж почати заняття з
дітьми, дайте їм можливість роздивитися палички. Спостерігайте за тим, як діти грають
з паличками: викладають узори, конструюють, розвивають сюжетно-рольову або
самостійну гру тощо. Можливо, уже в ході цих ігор дітям вдасться зробити власні
відкриття:
Смужок багато, вони різного кольору;
Є смужки однакових кольорів, є - різного;
Одні смужки довші, інші коротші.

45. Варіативність використання паличок Дж. Кюїзенера для розвитку логіко-математичних здібностей дошкільників Орієнтування на площині Побуд

Варіативність використання паличок Дж. Кюїзенера для розвитку логікоматематичних здібностей дошкільників
Орієнтування на площині
Побудувавши числову пряму (східці, потяг, гірку), діти можуть відповісти на такі
запитання:
- Яка паличка знаходиться праворуч від жовтої?
- Яка паличка знаходиться ліворуч від синьої?
- Які палички знаходяться праворуч (ліворуч) фіолетової?
Геометричні фігури
З паличок Дж. Кюїзенера можна викласти такі геометричні фігури як квадрат, ромб,
прямокутник, трикутник.
Можна викласти дві однакові фігури з різних паличок та порівняти їх. Наприклад,
викласти один квадрат з трійок (блакитних паличок), а інший – з пʼятірок (жовтих). Діти
порівнюють розміри квадратів. Який більше (менше)? Чому? Який квадрат буде більше:
з вісімок чи з десяток? Чому?
Лічба
На числовій прямій, що побудована з паличок діти можуть не лише рахувати їх у
прямому та зворотному порядку, але й виконувати інші види лічби. Це порядкова лічба,
лічба від будь-якого числа до заданого, лічба двійками, трійками. Тут також добре
видно суміжні числа або, як називають їх діти, «числа-сусіди». Суміжними є ті два
числа-палички, які стоять ліворуч та праворуч від заданого.

46. Логічне мислення Палички є чудовим матеріалом для розвитку логічного мислення. Дидактична гра для вправляння у розрізненні і групуванні п

Логічне мислення
Палички є чудовим матеріалом для розвитку логічного мислення.
Дидактична гра для вправляння у розрізненні і групуванні паличок (смужок) за
кольором, засвоєння назв кольорів
Гра «Квіти»
Матеріал: палички Дж. Кюїзенера, картки з трьома кружечками різних кольорів.
Хід: зла чаклунка перетворила квіти та кольорові круглі камінчики. Врятувати квіти
можуть кольорові палички. Діти викладають навколо круга-камінчика палички такого ж
кольору, як і він сам.

47. Дидактична гра на ознайомлення дітей з тим, що палички (смужки) одного кольору мають однакову довжину, формування вміння порівнювати їх за

Дидактична гра на ознайомлення дітей з тим, що палички (смужки) одного
кольору мають однакову довжину, формування вміння порівнювати їх за
довжиною та засвоєння їх послідовної залежності по довжині; вправляння у
порівнянні за висотою шириною та довжиною.
Гра «Будуємо плоти»
Матеріал: палички Дж. Кюїзенера, картки із зображенням вузької і широкої річок.
Хід: для подорожі потрібно збудувати 2 плоти: широкий і вузький. Усі дощечки у
кожному плоту мають бути однакової довжини. Діти будують два плоти, розміщують їх
на річці відповідної ширини.

48. Дидактична гра для формування у дітей вміння співвідносити колір та довжину палички (смужки) з числом і число з кольором та довжиною. Гра «В

Дидактична гра для формування у дітей вміння співвідносити
колір та довжину палички (смужки) з числом і число з кольором та довжиною.
Гра «Весела подорож на потязі»
Матеріал: палички Дж. Кюїзенера, картонний потяг.
Хід: дітям пропонується відправитись у подорож на потязі. Для цього вони викладають
вагони потяга з паличок від найкоротшої до найдовшої. Після цього розповідають про
свої потяги, даючи відповіді на запитання: Яким по порядку стоїть фіолетовий вагон?
Якого кольору третій вагон?...

49. Дидактична гра на ознайомлення дітей зі складом чисел, засвоєння ними кількісних відношень між числами. Гра «Килимок» Матеріал: палички Дж

Дидактична гра на ознайомлення дітей зі складом чисел, засвоєння ними кількісних
відношень між числами.
Гра «Килимок»
Матеріал: палички Дж. Кюїзенера, цифри.
Хід: дітям дається завдання сплести килимки з різних ниток-паличок. Ширина килимка
повинна дорівнювати числу, заданому вихователем. Діти «сплітають» килимки та
позначають їх ширину цифрою.

50. Дидактична гра для розвитку логічного мислення Гра «Розстав палички» Матеріал: палички Дж. Кюїзенера. Хід: діти беруть 4 палички, та розстав

Дидактична гра для розвитку логічного мислення
Гра «Розстав палички»
Матеріал: палички Дж. Кюїзенера.
Хід: діти беруть 4 палички, та розставляють їх за вказівкою вихователя. Вказівка може
бути такою: Рожева паличка повинна бути між жовтою і чорною, а чорна поряд із
синьою.

51. Конструювання Палочки та смужки Дж. Кюїзенера є чудовий матеріал для конструювання. З паличок можна конструювати безліч предметів або віз

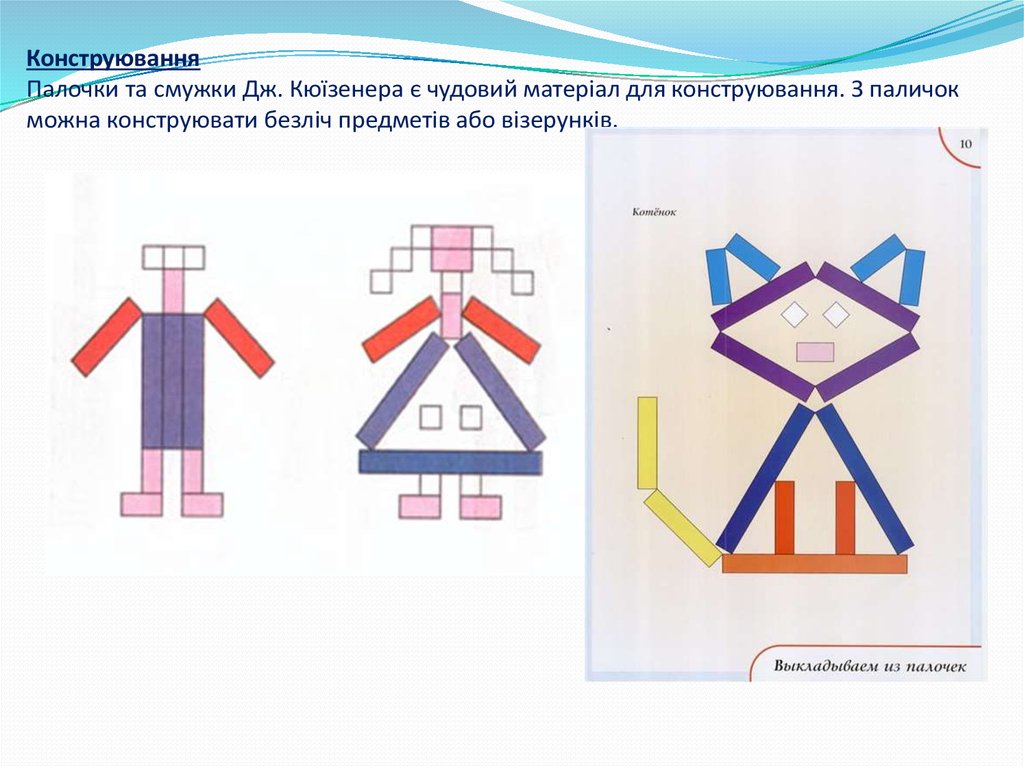
Конструювання
Палочки та смужки Дж. Кюїзенера є чудовий матеріал для конструювання. З паличок
можна конструювати безліч предметів або візерунків.

52. Гра-головоломка «Танграм» Танграм (з кит. «сім дощечок майстерності») — це головоломка, яка складається з семи гральних кісток — пласких

Гра-головоломка «Танграм»
Танграм (з кит. «сім дощечок майстерності») — це головоломка, яка складається з семи
гральних кісток — пласких геометричних фігур, які називають танами, що складаються
у різні форми. Завдання головоломки — створити задану форму (на підставі лише
обрису силуету) з використанням всіх семи танів, які заборонено накладати один на
один. Це одна з найбільш популярних головоломок такого типу у світі.
За допомогою танграму можна складати не тільки фігури тварин і предметів, але й
букви і цифри.

53. Чим же так танграм захоплює увесь світ вже більше двох тисяч років? Сприяє: вивченню простих геометричних фігур і їх ознак; розвиває уяву, л

Чим же так танграм захоплює увесь світ вже більше двох тисяч років?
Сприяє:
вивченню простих геометричних фігур і їх ознак;
розвиває уяву, логіку, спостережливість;
розвиває образне та просторове мислення;
вчить сприйняттю форми, розміру та кольору;
активній і практичній діяльності під час створення малюнку;
розвиває вміння аналізувати прості зображення.

54. Гра дуже проста у виготовленні. Квадрат 8х8 см з картону, пластику, однаково розфарбований з двох сторін розрізають на 7 частин. У результаті

Гра дуже проста у виготовленні. Квадрат 8х8 см з картону, пластику, однаково
розфарбований з двох сторін розрізають на 7 частин. У результаті виходить 2
великих, 1 середній і 2 маленьких трикутник, квадрат і паралелограм.
Використовуючи всі 7 частин, щільно приєднуючи їх один до одного, можна
скласти дуже багато різних зображень за зразками і за власним задумом.
В результаті вправ і завдань до цієї гри дитина навчиться аналізувати прості
зображення, виділяти в них геометричні фігури, навчиться візуально розбивати
цілий об'єкт на частини і навпаки складати з елементів задану модель.

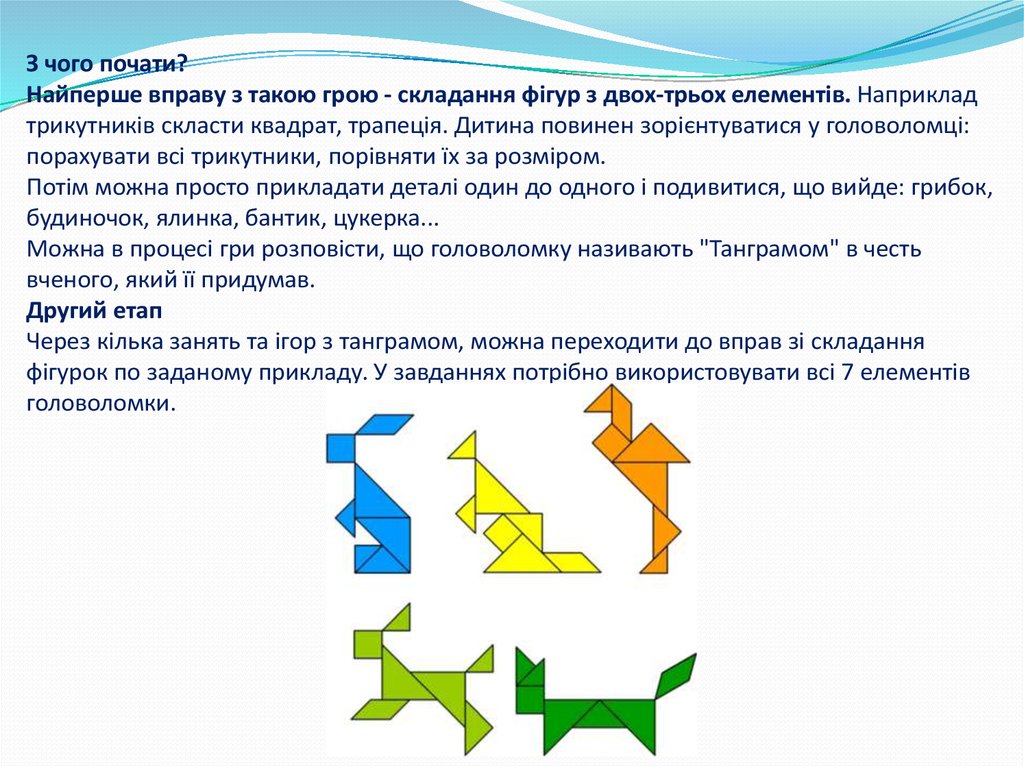
55. З чого почати? Найперше вправу з такою грою - складання фігур з двох-трьох елементів. Наприклад трикутників скласти квадрат, трапеція. Дитин

З чого почати?
Найперше вправу з такою грою - складання фігур з двох-трьох елементів. Наприклад
трикутників скласти квадрат, трапеція. Дитина повинен зорієнтуватися у головоломці:
порахувати всі трикутники, порівняти їх за розміром.
Потім можна просто прикладати деталі один до одного і подивитися, що вийде: грибок,
будиночок, ялинка, бантик, цукерка...
Можна в процесі гри розповісти, що головоломку називають "Танграмом" в честь
вченого, який її придумав.
Другий етап
Через кілька занять та ігор з танграмом, можна переходити до вправ зі складання
фігурок по заданому прикладу. У завданнях потрібно використовувати всі 7 елементів
головоломки.

56. Третій етап Більш складною і цікавою для дітей є відтворення фігур за зразками-контурами. Це третій етап освоєння гри. Відтворення фігур по

контурах вимагає зорового членування
форми на складові частини, тобто на
геометричні фігури. Такі завдання у дитячих садках рекомендують пропонувати дітям з
6-7 років .
Одне з перших завдань на цьому етапі - біжить гусак, почніть краще з нього. Спочатку,
проаналізуйте разом з дитиною, їх яких частин може складатися голова, шия, лапи
гусака. Можна їх зробити їх інших деталей...
Довше можна прикладати різні елементи головоломки, шукаючи правильний результат.

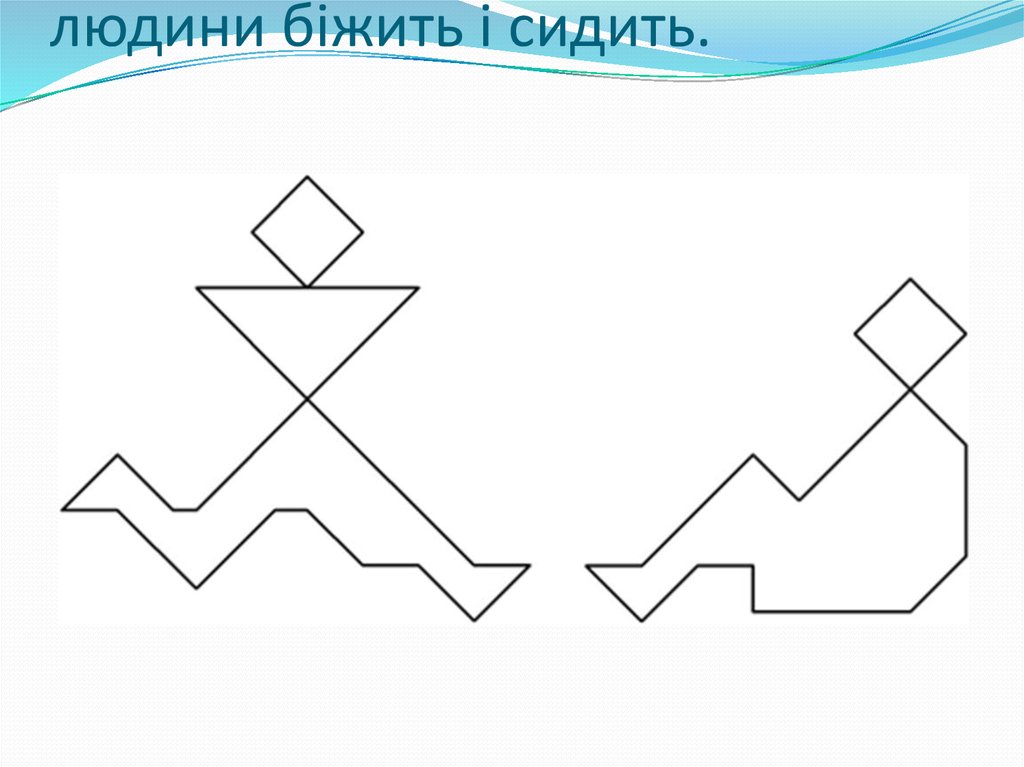
57. Це вже складніше - фігури людини біжить і сидить.    

людини біжить і сидить.

58. Червертий етап Тут вже діти можуть збирати зображення за своїм задумом. Картинку спочатку замислюють подумки, потім збирають окремі част

Червертий етап
Тут вже діти можуть збирати зображення за своїм задумом. Картинку спочатку
замислюють подумки, потім збирають окремі частини, після цього створюється
вся картинка.

59. Блоки Дьенеша - універсальна розвиваюча гра У багатьох країнах світу успішно використовується дидактичний матеріал "Логічні блоки", розро

Блоки Дьенеша - універсальна розвиваюча гра
У багатьох країнах світу успішно використовується дидактичний матеріал "Логічні
блоки", розроблений угорським психологом і математиком Дьенеша для розвитку
логічного мислення у дітей.
Останнє десятиріччя цей матеріал завойовує все більше визнання у педагогів і батьків
нашої країни.
Логічні блоки Дьенеша представляють собою набір з 48 геометричних фігур:
а) чотирьох форм (коло, трикутник, квадрат, прямокутник);
б) чотирьох кольорів (червоний, синій, жовтий);
в) двох розмірів (великий, маленький);
г) двох видів товщини (товстий, тонкий).
Кожна геометрична фігура характеризується чотирма ознаками: формою, кольором ,
розміром, товщиною. У наборі немає жодної однакової фігури.

60. Дидактична гра «Ланцюжок» Мета:Навчити викладати блоки з певною послідовністю: синій, червоний, синій, червоний. Або коло, трикутник, коло,

Дидактична гра «Ланцюжок»
Мета:Навчити викладати блоки з певною послідовністю: синій, червоний, синій,
червоний. Або коло, трикутник, коло, трикутник. Додайте третю фігуру. Можна
ускладнити завдання - викласти ланцюжок, але пропустити середину. Запропонувати
зібрати доріжку, щоб кожна наступна фігура відрізнялася від попередньої однією
ознакою.
Коли дитина засвоїть найпростіші логічні операції - переходьте до більш складного
завдання.
Сховайте одну фігуру. Дитина повинна вгадати, який саме блок захований, вихователь
задає навідні запитання, відповідь на які тільки «так» або «ні». Наприклад, дитина
питає - ця фігура квадратна? Ні. Разом прибирає всі круглі форми. - Вона червона? Ні.
Прибирає червоні.

61. Дидактична гра "Скільки?" Матеріал: логічні блоки. Мета гри: розвивати вміння ставити запитання і розвивати вміння виділяти властивості. Хі

Дидактична гра "Скільки?"
Матеріал: логічні блоки.
Мета гри: розвивати вміння ставити запитання і розвивати вміння виділяти властивості.
Хід гри: Діти діляться на дві команди. Вихователь розкладає логічні фігури в будь-якому
порядку і пропонує дітям придумати питання, що починаються зі слів "... Скільки"
За кожну правильне питання фішка. Виграє команда, яка набрала більшу кількість
фішок.
Варіанти питань: "Скільки великих фігур?" "Скільки червоних фігур в першому ряду?"
(По горизонталі), "Скільки кіл?" і т.д.

62. Дидактична гра «Що змінилося» Мета:удосконалювати знання дітей про геометричні фігури, їх кольорі, величину, товщину;розвивати мислення. М

Дидактична гра «Що змінилося»
Мета:удосконалювати знання дітей про геометричні фігури, їх кольорі, величину,
товщину;розвивати мислення.
Матеріал: Набір Блоків Дьенеша.
Хід гри: Перед дитиною на стіл викладається кілька фігур, які потрібно запам'ятати, а
потім одна з фігур зникає або замінюється на нову, або дві фігури міняються місцями.
Дитина повинна помітити зміни.

63. Охарактеризуйте послідовність навчання дітей вимірювання довжини умовною міркою. Розкрийте важливість використання дітьми дошкільного

Охарактеризуйте послідовність
навчання дітей вимірювання
довжини умовною міркою.
Розкрийте важливість
використання дітьми дошкільного
віку вимірювання в різних видах
діяльності.

64. Охарактеризуйте послідовність навчання дітей вимірювання довжини умовною міркою. Розкрийте важливість використання дітьми дошкільного

Охарактеризуйте послідовність навчання дітей вимірювання довжини
умовною міркою. Розкрийте важливість використання дітьми дошкільного
віку вимірювання в різних видах діяльності.
Діти дошкільного віку ми вчимо сприймати
величину предметів на чуттєвій основі: за
допомогою аналізаторів (зорового, рухового,
слухового).
Внаслідок дій з предметами та цілеспрямованого
навчання діти вчаться розрізняти величини
шляхом порівняння. За допомогою слова діти
визначають і розрізняють ознаки величини
(коротша-давша)

65.

Поступово дітей підводять до необхідності
точнішого опосередкованого порівняння величини
вимірюванням. Дітей ознайомлюють з
вимірюванням умовними мірками.
Навчання вимірюванню довжини умовними
мірками. Умовними мірками при вимірюванні
довжини можуть бути: смужки паперу, мотузки,
стрічки, палички, відстань – кроками, пальцями,
ліктями, руками.

66.

Міри та вимірюваний предмет вихователь заздалегідь заготовлює так,
щоб умовна міра помістилась у вимірюваному предметі кілька разів.
Вихователь показує і розповідає дітям, як накладати міри: щільно
тримаючи, приставляючи одну до одної, щоб між ними не залишалось
простору і щоб одна міра не накладалась на другу.

67. Навчання дітей вимірюванню проходить поетапно

І етап – навчання дітей вимірювання за допомогою
багатьох умовних мірок.
Умовні мірки рахуються в кінці вимірювання

68.

ІІ етап – вимірювання за допомогою однієї умовної мірки та
відставлення риски позначки. В кінці вимірювання рахується кількість
скільки разів мірка помістилась в довжину.

69.

ІІІ етап – використання однієї умовної мірки та відставлення фішки. В кінці
вимірювання рахується кількість фішок.

70.

IV етап – поєднання лічби і вимірювання.

71. Методика формування часових уявлень у дітей дошкільного віку

Виконала:
Крупинська Ірина Дмитрівна
4-А курс

72. Орієнтування в часі 2-3х річних дітей ( ранній вік).

Діти дошкільного віку починають сприймати час і
пізнавати, в основному чуттєво. Дитину привчають
вночі більше спати, а в день – гратися, у визначний час
дня вчитися. Спілкуючись з дорослим дитина
поповнює свій словниковий запас такими словами як (
незабаром, зараз, потім), частини доби ( день, ніч), а
також слова які відображають плинність часу (
сьогодні, завтра). В ранньому віці діти вже розрізняють
і правильно називають дієслова теперішнього,
минулого та майбутнього часу ( ми ходили, підемо,
йдемо). Проте часові уявлення мають значно
індивідуальні відмінності, зумовлені навчанням і
вихованням дитини.

73. Орієнтування в часі дітей молодшого дошкільного віку.

Спочатку молодші дошкільнята характеризують час
за подіями, що відбулися безпосередньо з кожним
іх них за день, і викликали сильні емоції,
поступово вони відходять від такого розуміння часу
і починають пов'язувати його з подіями.
Дітей 4р. Життя вчать розуміти і правильно
вживати слова, що вказують на час дії: було, буде, є.
Розрізняють і називають частини доби ( ранок,
день, вечір, ніч).
Формується насамперед чіткіше розпорядок дня.

74. Орієнтування в часі дітей 5-го року життя( середнього дошкільного віку)

У цій віковій групі уточнюються уявлення дітей про деякі відрізки часу,
частини доби. Дітей навчають послідовно оцінювати дії: була, є, буде.
Вихователь з'ясовує з дітьми, що роблять вранці, вдень, ввечері та вночі.
Як прийом навчання широко використовуються – спостереження, розгляд
картин, ілюстрацій, читання, бесіди, рідні дидактичні ігри. Як словесний
матеріал можна використовувати оповідання, вірші, загадки про частини
доби.
Закріплюється поняття “доба”.
Під впливом навчання діти усвідомлюють, що доба завжди змінює одна
одну.
На основі формування просторових і часових уявлень у дітей 5-го року
життя можна починати формувати в них початкові єдині просторовічасові уявлення і поняття про швидкість. ( швидко, повільно).
Для цього можна використовувати зображення транспортів, а для
порівняння, рух пішоходів, черепахи.

75. Орієнтування в часі дітей старшого дошкільного віку:

У дітей 6р. життя поглиблюються і закріплюються знання. Діти
ознайомлюються з порами року, днями тижня. Для того щоб краще
запам'ятати - дітям пояснюють походження назв днів тижня. Вихователь
зосереджує увагу на том скільки днів люди працюють і скільки
відпочивають. Також використовують картинки-символи із зображенням
усіх днів тижня.
У старшій групі вихователь формує у дітей “відчуття часу”, розуміння
значення його в житті людей.

76.

Демонстраційний дидактичний
матіріал

77.

78.

У старшому дошкільному віці необхідно закріплювати
знання дітей про добу і продовжувати знайомити дітей
за допомогою календаря з: тижнем, місяцями, роком.

79.

А також – у старшому дошкільному віці
паралельно у дітей необхідно розвивати
почуття часу, почати знайомити з тривалістю
таких заходів часу, як 1 хвилина, 3, 5, 10 хвилин,
півгодини і година.