Similar presentations:
Правильные многогранники
1. Правильные многогранники
2. Правильный многогранник -это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной си
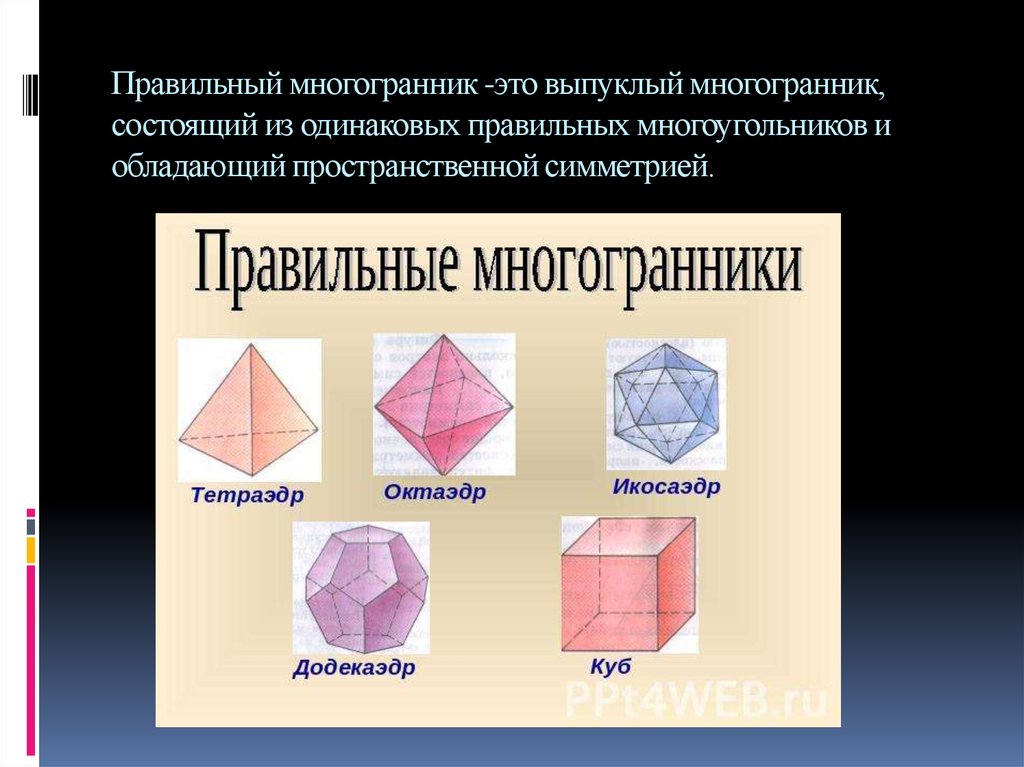
Правильный многогранник -это выпуклый многогранник,состоящий из одинаковых правильных многоугольников и
обладающий пространственной симметрией.
3. Тетраэдр – простейший многогранник, гранями которого являются четыре треугольника, треугольная пирамида. У тетраэдра 4 грани, 4 вершины и 6
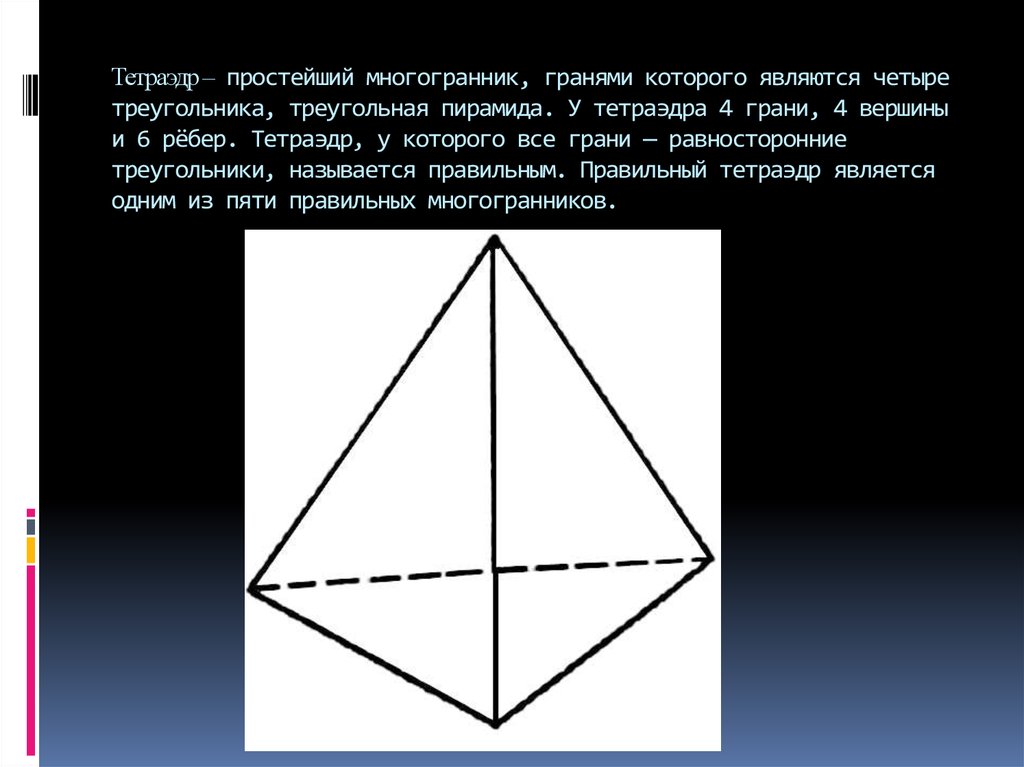
Тетраэдр – простейший многогранник, гранями которого являются четыретреугольника, треугольная пирамида. У тетраэдра 4 грани, 4 вершины
и 6 рёбер. Тетраэдр, у которого все грани — равносторонние
треугольники, называется правильным. Правильный тетраэдр является
одним из пяти правильных многогранников.
4. Октаэдр — многогранник с восемью гранями. Правильный октаэдр является одним из пяти выпуклых правильных многогранников, так называемых
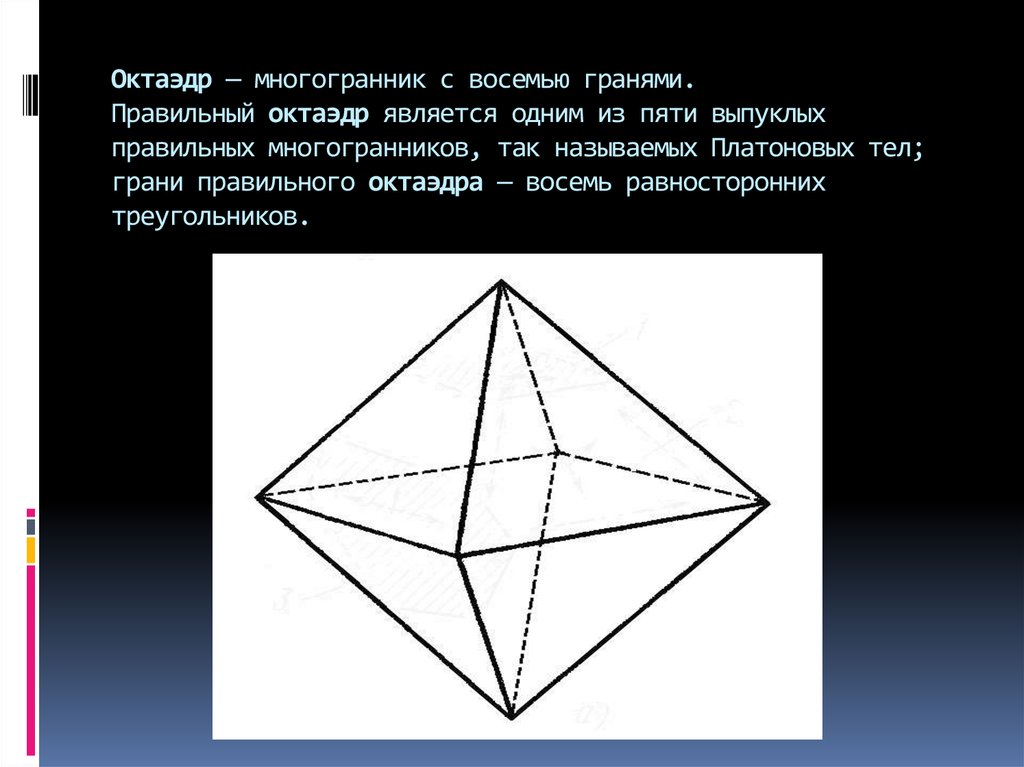
Октаэдр — многогранник с восемью гранями.Правильный октаэдр является одним из пяти выпуклых
правильных многогранников, так называемых Платоновых тел;
грани правильного октаэдра — восемь равносторонних
треугольников.
5. Икосаэдр — правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел. Каждая из 20 граней представляет собой равносторонн
Икосаэдр — правильный выпуклый многогранник, двадцатигранник, одно изПлатоновых тел. Каждая из 20 граней представляет собой равносторонний
треугольник. Число ребер равно 30, число вершин — 12.
6. Додекаэдр — один из пяти возможных правильных многогранников. Додекаэдр составлен из двенадцати правильных пятиугольников, являющихся
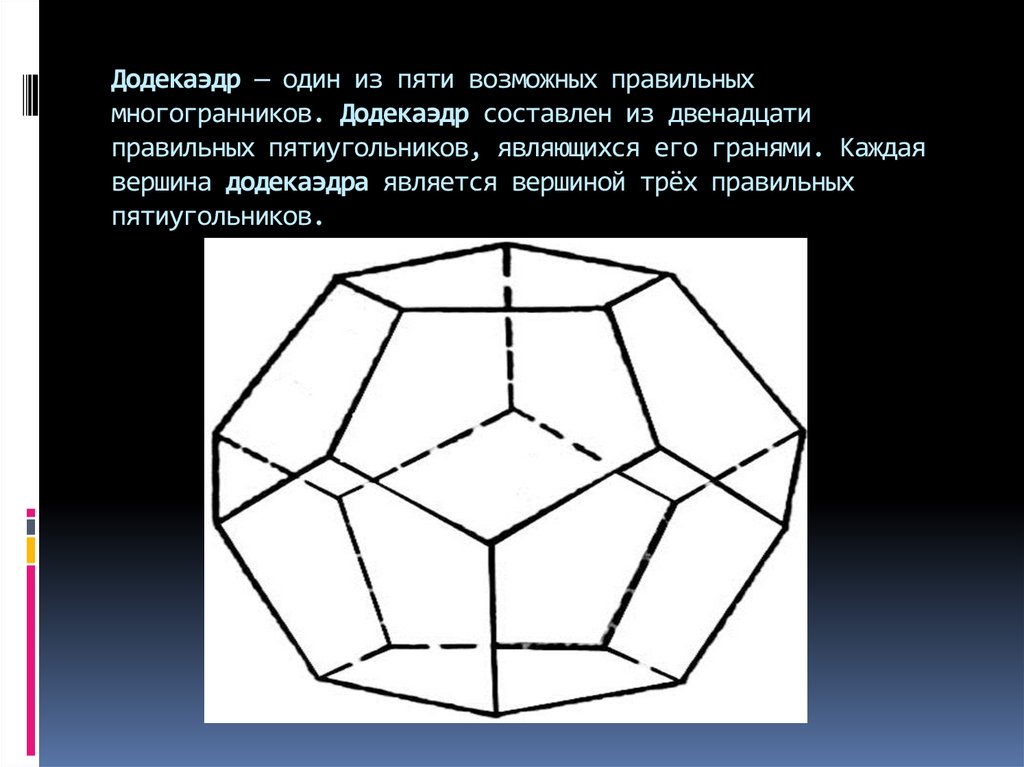
Додекаэдр — один из пяти возможных правильныхмногогранников. Додекаэдр составлен из двенадцати
правильных пятиугольников, являющихся его гранями. Каждая
вершина додекаэдра является вершиной трёх правильных
пятиугольников.
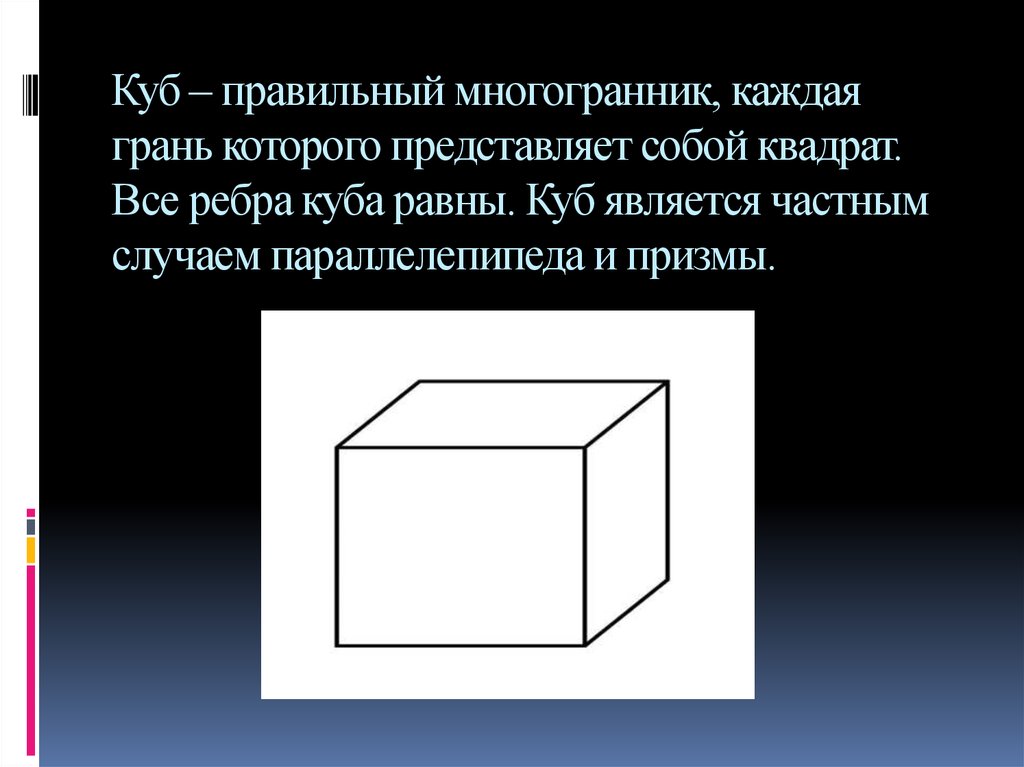
7. Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны. Куб является частным случаем парал
Куб – правильный многогранник, каждаягрань которого представляет собой квадрат.
Все ребра куба равны. Куб является частным
случаем параллелепипеда и призмы.
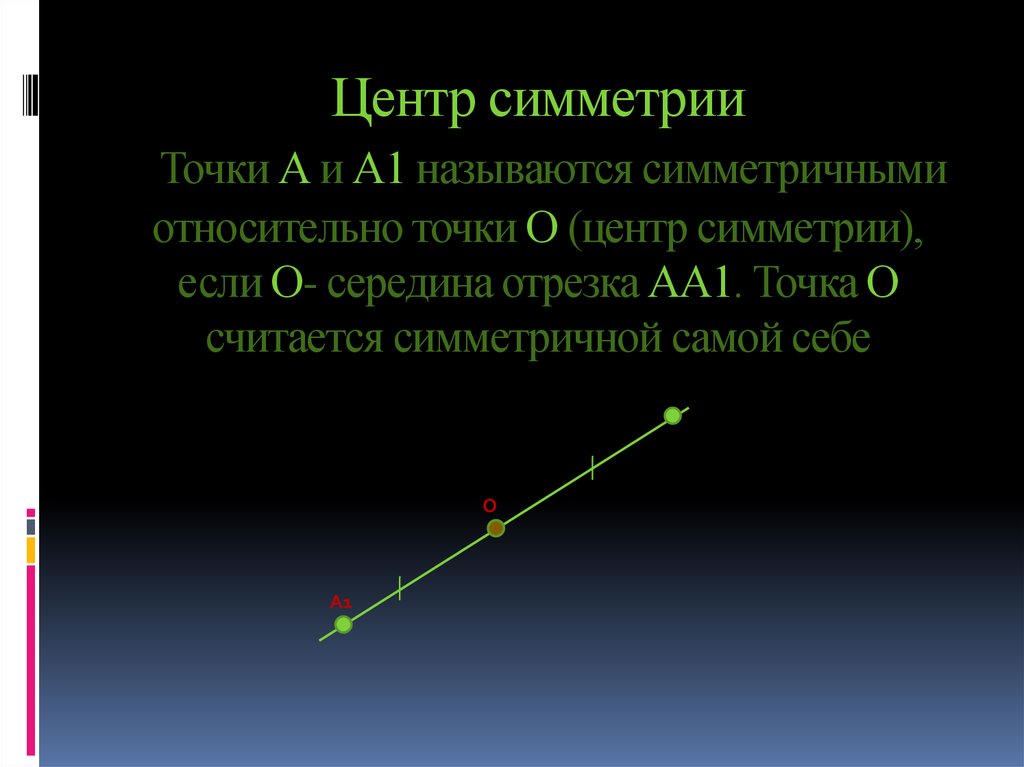
8. Центр симметрии Точки А и А1 называются симметричными относительно точки О (центр симметрии), если О- середина отрезка АА1. Точка О считается
симметричной самой себеО
А1
9. Ось симметрии Точки А и А1 называются симметричными относительно прямой а(ось симметрии), если прямая а проходит через середину отрезка АА1
Ось симметрииТочки А и А1 называются симметричными
относительно прямой а(ось симметрии), если
прямая а проходит через середину отрезка
АА1 и перпендикулярна к этому. Каждая точка
прямой а считается симметричной самой себе
10. Плоскость симметрии Точки А и А1 называются симметричными относительно плоскости α(плоскость Симметрии),если плоскость α проходит через с
Плоскость симметрииТочки А и А1 называются симметричными
относительно плоскости α(плоскость
Симметрии),если плоскость α проходит через
середину отрезка АА1 и перпендикулярна к
этому отрезку. Каждая точка плоскости α
считается симметричной самой себе.




 mathematics
mathematics








