Минимизация стоимости выполнения работ при ограничении на время их выполнения

1. Оптимальные назначения, использующие вектор неоднородных критериев

Лекция 4

2. Задача 1: минимизация стоимости выполнения работ при ограничении на время их выполнения

2
Задача 1: минимизация стоимости
выполнения работ при ограничении на
время их выполнения
Задача отличается от ранее рассмотренной тем,
что кроме стоимости известно время
выполнения каждым рабочим каждой работы.
Если i-й рабочий не может выполнять j-ю
работу, то:
r
(
i
,
j
)
r
(
i
,
j
)
,
1
2
где:
r1(i,j) – стоимость выполнения i-ым рабочим j-ой
работы.
r2(i,j) – время выполнения i-ым рабочим j-ой
работы
Т – плановый период.

3. Формальная постановка задачи 1

3
Формальная постановка задачи 1
n n
r1 (i, j ) y (i, j ) min; - целевая функция - минимизация затрат
i 1 j 1
max max r2 (i, j ) y (i, j ) T ; - ограничение на время выполненя плана Т
j
i
n
y (i, j ) 1; j 1,2,..., n; - каждая работа должна быть выполнена
i 1
n
j (i, j ) 1; i 1,2,..., n; - каждый рабочий должен иметь работу
j 1
y (i, j ) 1,0; i 1,2,..., n. j 1,2,..., n; - булевы переменные

4. Решение задачи 1

(i, j) U : r2 (i, j) T
r1 (i, j)
Решение задачи 1
• Решение задачи 1 сводится к решению
«классической» задачи о назначениях, если
исходную матрицу М преобразовать в M’
следующим образом:
(i, j) U : r2 (i, j) T r1 (i, j) .
• Иными словами считаем, что если время
выполнения i-м рабочим j-й работы больше Т, то
i-й рабочий не может делать j-ю работу.
• После этого матрица М’, содержащая лишь r1(i,j),
используется для решения «классической» задачи
о назначениях.
4

5. ПРИМЕР 1

5
ПРИМЕР 1
Решить задачу с вектором
критериев на бихроматическом
графе, заданном (n x n) матрицей
М, если n = 4, в верхней части
каждой ячейки (i,j) матрицы М
приведены величины r1(i,j), а в
нижней – r2(i,j). Верхняя граница
времени выполнения всех работ Т
= 12.

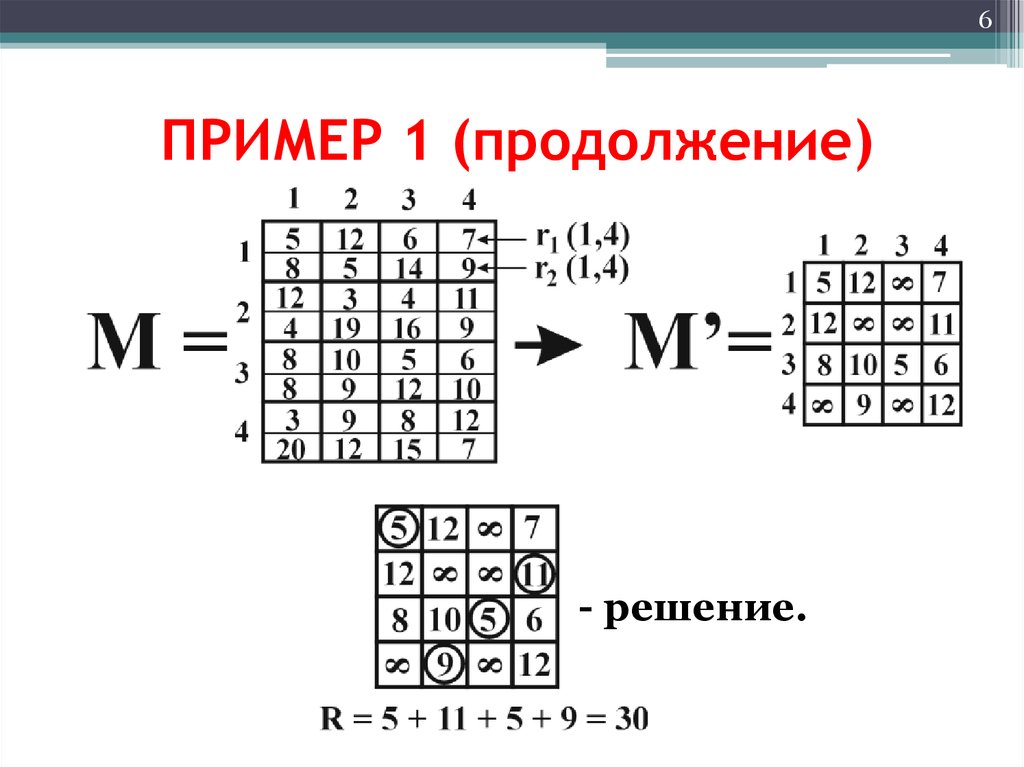
6. ПРИМЕР 1 (продолжение)

6
ПРИМЕР 1 (продолжение)
- решение.

7. РЕШИТЬ САМОСТОЯТЕЛЬНО

7
РЕШИТЬ САМОСТОЯТЕЛЬНО
24
12
30
6
14
22
10
26
18
18
20
16
15
21
28
18
11
24
17
19
16
19
27
10
9
20
12
24
5
30
28
8
T 20;
C min .

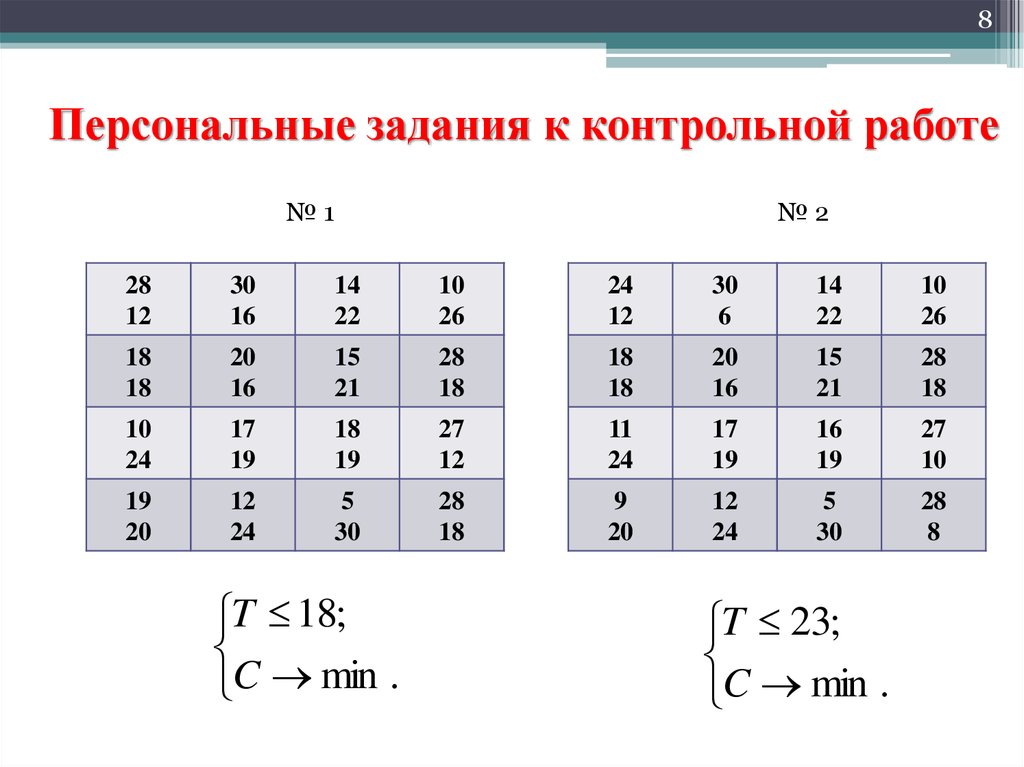
8. Персональные задания к контрольной работе

8
Персональные задания к контрольной работе
№1
№2
28
12
30
16
14
22
10
26
24
12
30
6
14
22
10
26
18
18
20
16
15
21
28
18
18
18
20
16
15
21
28
18
10
24
17
19
18
19
27
12
11
24
17
19
16
19
27
10
19
20
12
24
5
30
28
18
9
20
12
24
5
30
28
8
T 18;
C min .
T 23;
C min .

9. Персональные задания к контрольной работе

9
Персональные задания к контрольной работе
№3
№4
28
11
30
16
14
12
10
26
24
12
30
6
14
22
10
26
18
15
20
16
15
21
28
18
18
18
20
16
15
21
28
18
10
24
17
19
18
19
27
12
11
24
17
19
16
19
27
10
19
20
12
24
5
30
28
18
9
20
12
24
5
30
28
8
T 19;
C min .
T 24;
C min .

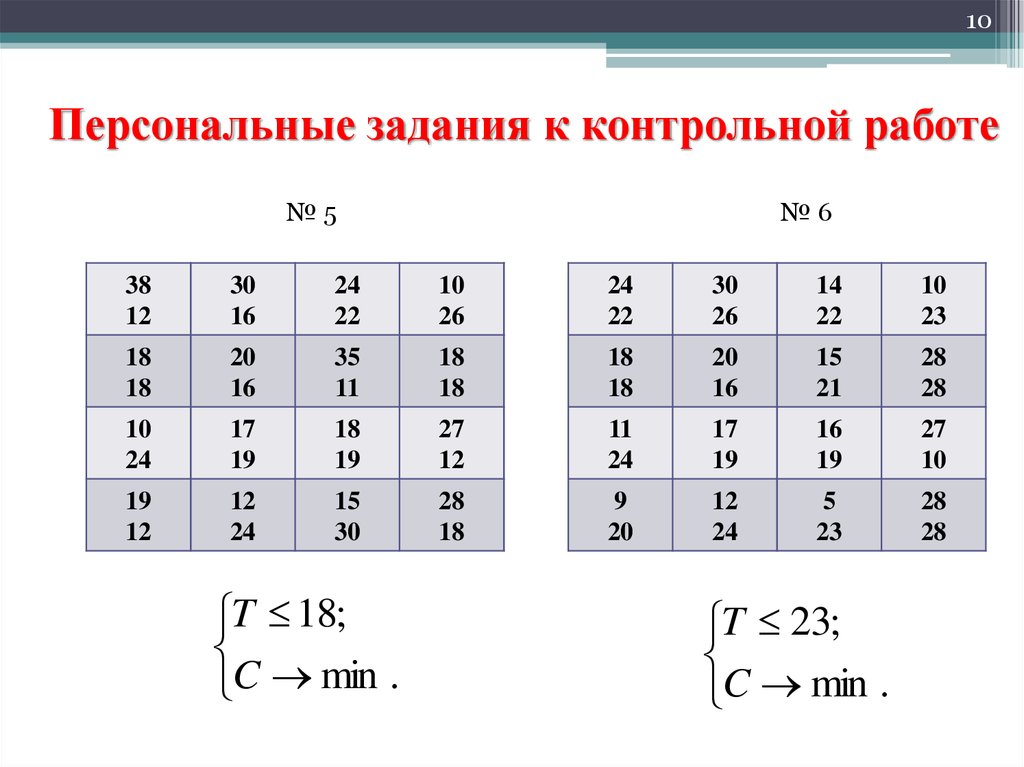
10. Персональные задания к контрольной работе

10
Персональные задания к контрольной работе
№5
№6
38
12
30
16
24
22
10
26
24
22
30
26
14
22
10
23
18
18
20
16
35
11
18
18
18
18
20
16
15
21
28
28
10
24
17
19
18
19
27
12
11
24
17
19
16
19
27
10
19
12
12
24
15
30
28
18
9
20
12
24
5
23
28
28
T 18;
C min .
T 23;
C min .

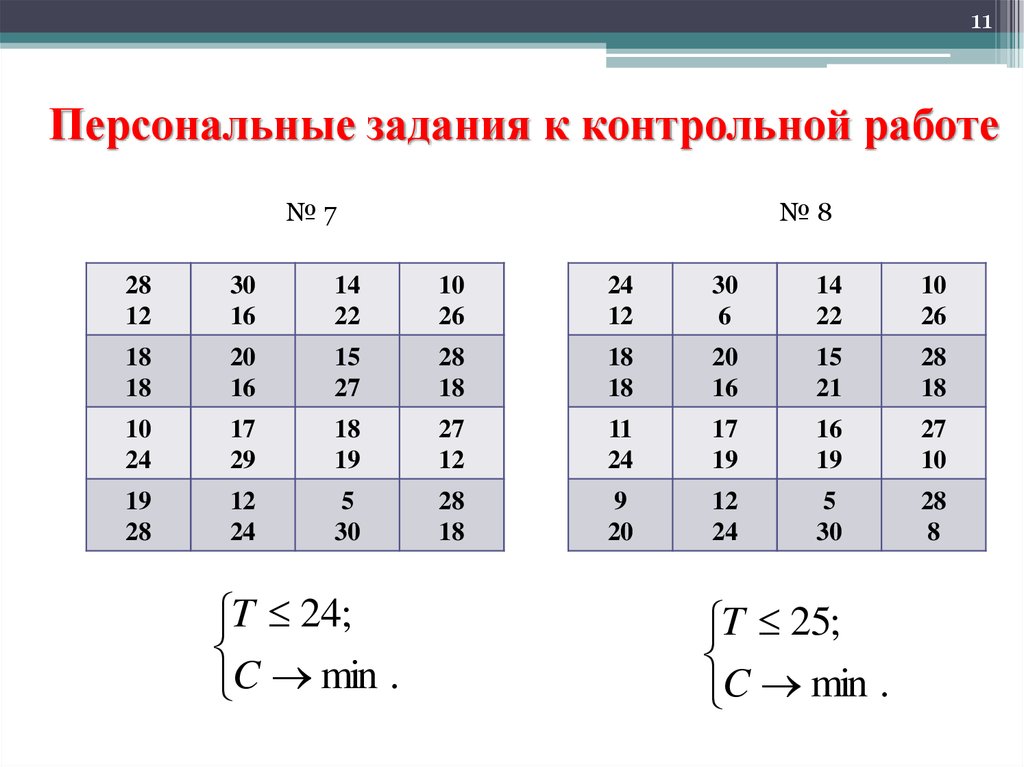
11. Персональные задания к контрольной работе

11
Персональные задания к контрольной работе
№7
№8
28
12
30
16
14
22
10
26
24
12
30
6
14
22
10
26
18
18
20
16
15
27
28
18
18
18
20
16
15
21
28
18
10
24
17
29
18
19
27
12
11
24
17
19
16
19
27
10
19
28
12
24
5
30
28
18
9
20
12
24
5
30
28
8
T 24;
C min .
T 25;
C min .

12. Персональные задания к контрольной работе

12
Персональные задания к контрольной работе
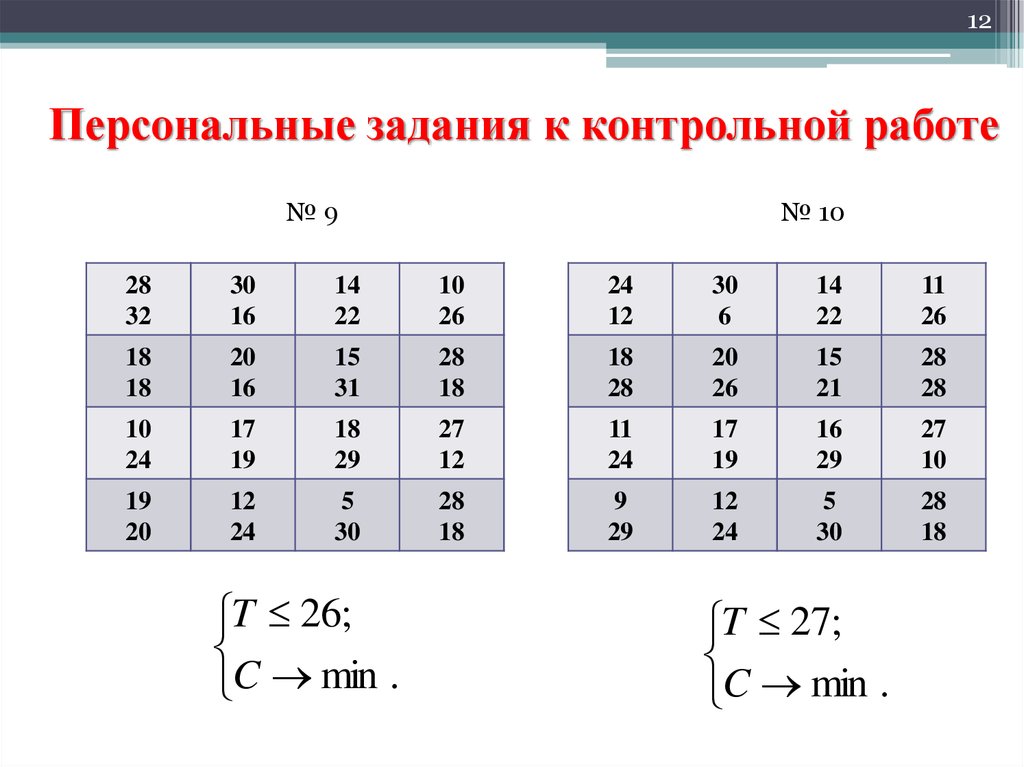
№9
№ 10
28
32
30
16
14
22
10
26
24
12
30
6
14
22
11
26
18
18
20
16
15
31
28
18
18
28
20
26
15
21
28
28
10
24
17
19
18
29
27
12
11
24
17
19
16
29
27
10
19
20
12
24
5
30
28
18
9
29
12
24
5
30
28
18
T 26;
C min .
T 27;
C min .

13. Персональные задания к контрольной работе

13
Персональные задания к контрольной работе
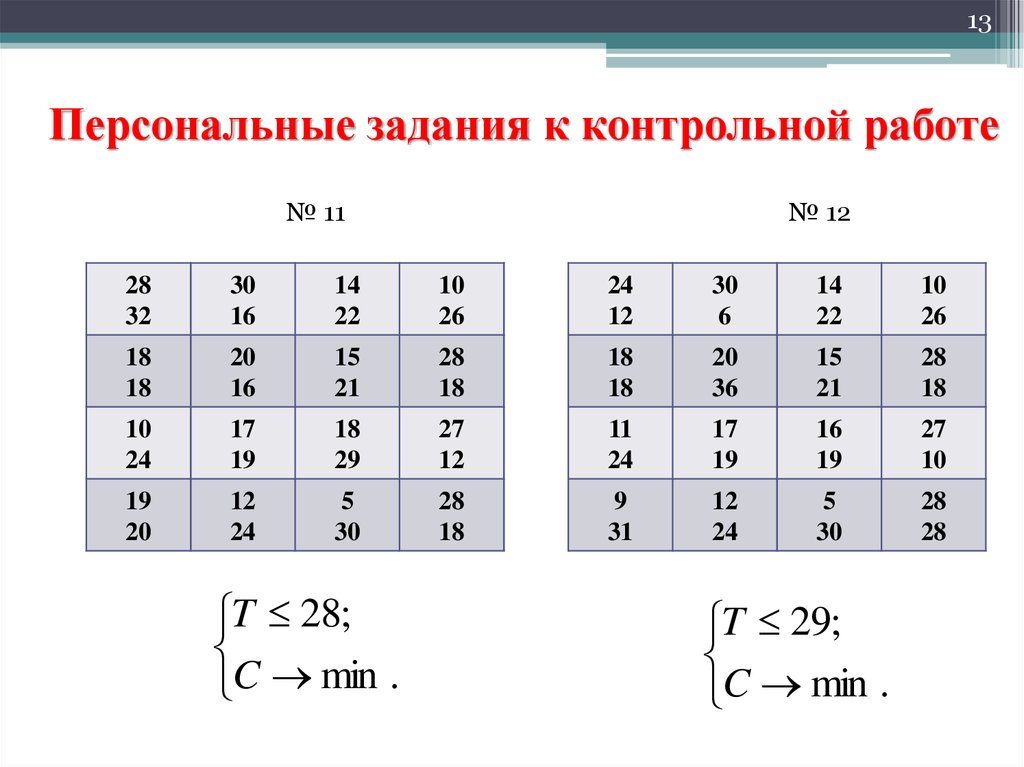
№ 11
№ 12
28
32
30
16
14
22
10
26
24
12
30
6
14
22
10
26
18
18
20
16
15
21
28
18
18
18
20
36
15
21
28
18
10
24
17
19
18
29
27
12
11
24
17
19
16
19
27
10
19
20
12
24
5
30
28
18
9
31
12
24
5
30
28
28
T 28;
C min .
T 29;
C min .

14. Персональные задания к контрольной работе

14
Персональные задания к контрольной работе
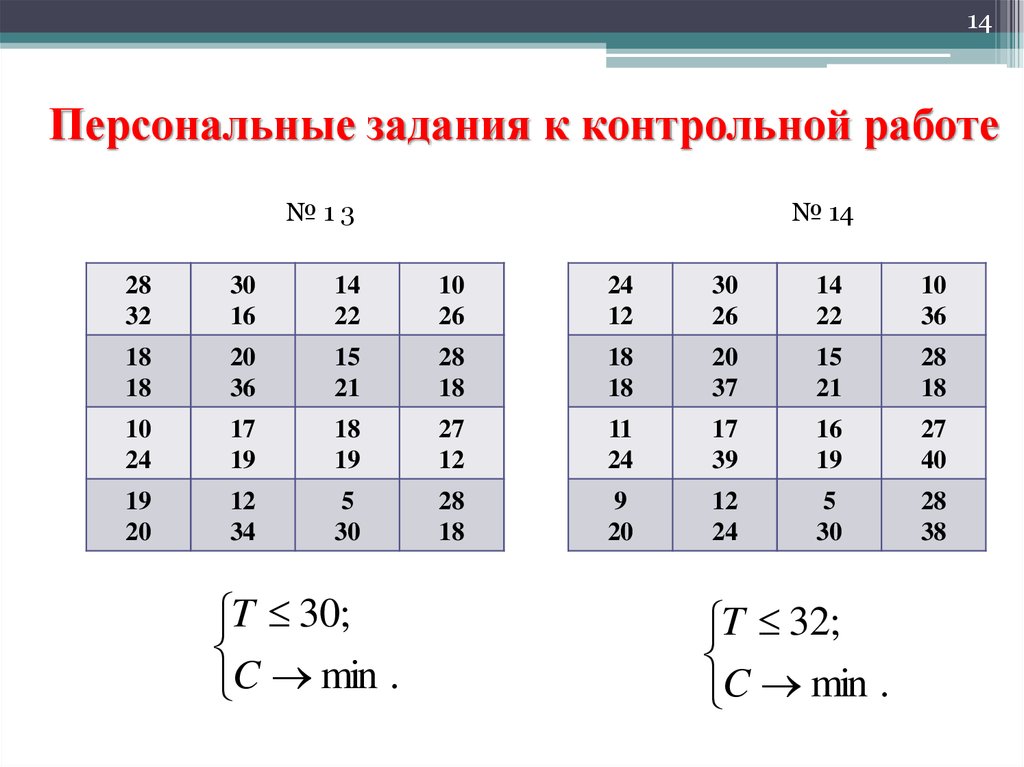
№13
№ 14
28
32
30
16
14
22
10
26
24
12
30
26
14
22
10
36
18
18
20
36
15
21
28
18
18
18
20
37
15
21
28
18
10
24
17
19
18
19
27
12
11
24
17
39
16
19
27
40
19
20
12
34
5
30
28
18
9
20
12
24
5
30
28
38
T 30;
C min .
T 32;
C min .

15. Персональные задания к контрольной работе

15
Персональные задания к контрольной работе
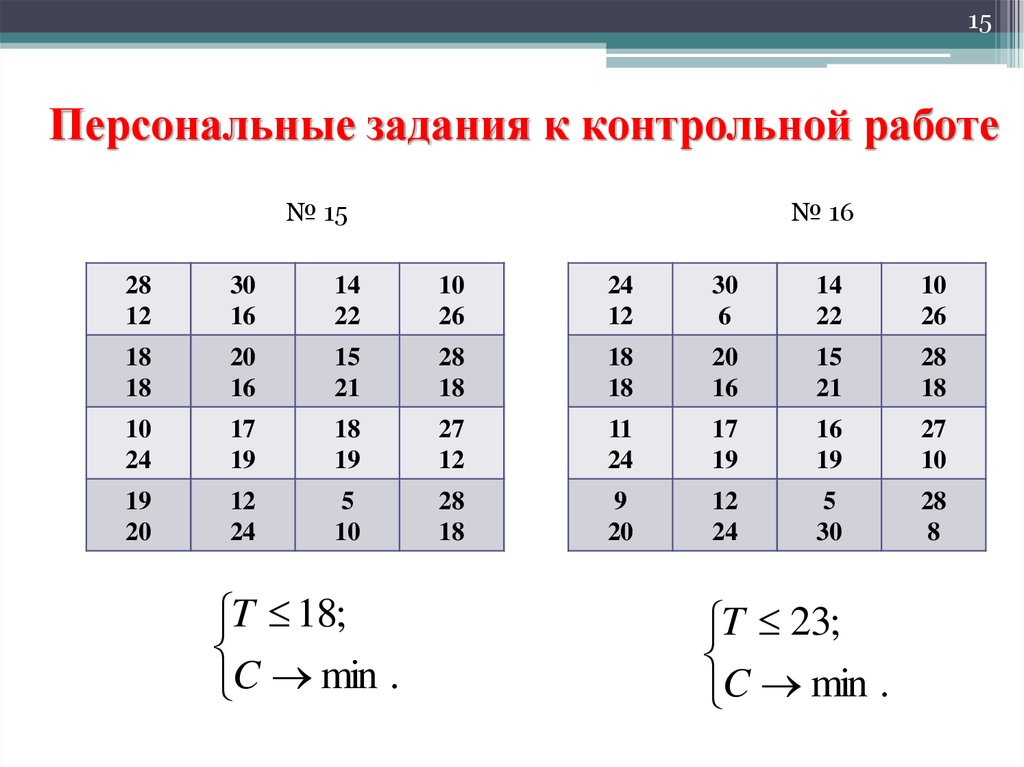
№ 15
№ 16
28
12
30
16
14
22
10
26
24
12
30
6
14
22
10
26
18
18
20
16
15
21
28
18
18
18
20
16
15
21
28
18
10
24
17
19
18
19
27
12
11
24
17
19
16
19
27
10
19
20
12
24
5
10
28
18
9
20
12
24
5
30
28
8
T 18;
C min .
T 23;
C min .

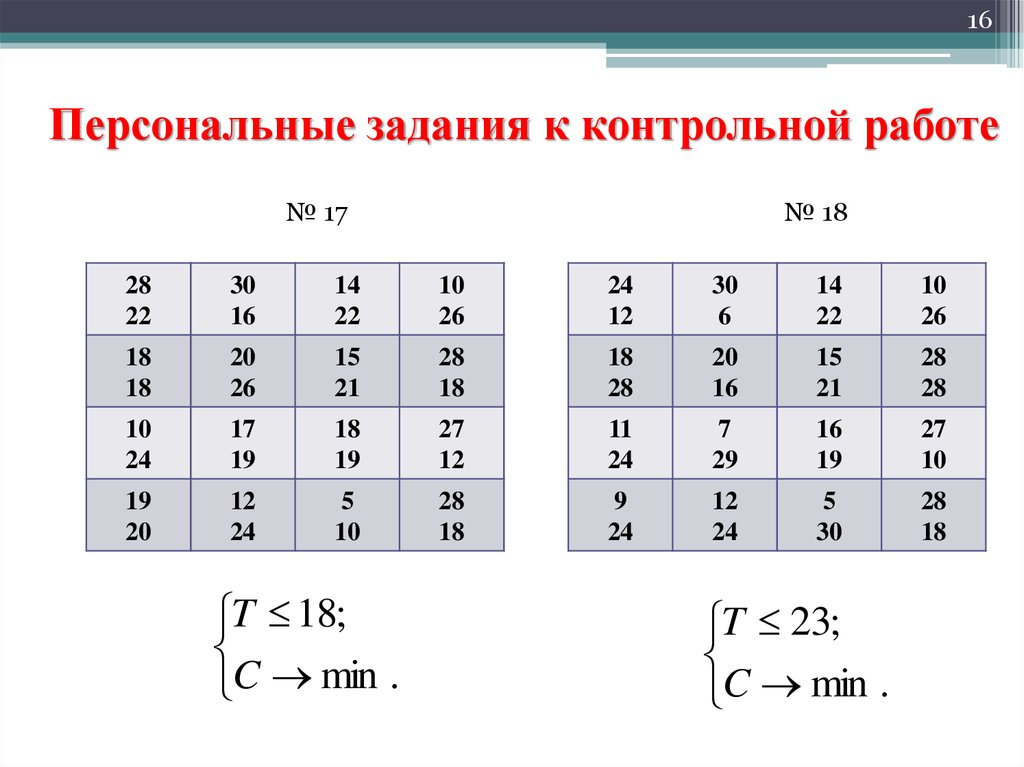
16. Персональные задания к контрольной работе

16
Персональные задания к контрольной работе
№ 17
№ 18
28
22
30
16
14
22
10
26
24
12
30
6
14
22
10
26
18
18
20
26
15
21
28
18
18
28
20
16
15
21
28
28
10
24
17
19
18
19
27
12
11
24
7
29
16
19
27
10
19
20
12
24
5
10
28
18
9
24
12
24
5
30
28
18
T 18;
C min .
T 23;
C min .

17. Персональные задания к контрольной работе

17
Персональные задания к контрольной работе
№ 19
№ 20
28
18
30
16
14
12
10
26
24
12
30
26
14
22
10
26
18
18
20
26
15
21
28
18
18
18
20
16
15
21
28
18
10
24
17
17
18
19
27
12
11
24
17
19
16
29
27
10
19
16
12
24
5
20
28
18
9
20
12
24
5
30
28
38
T 18;
C min .
T 23;
C min .

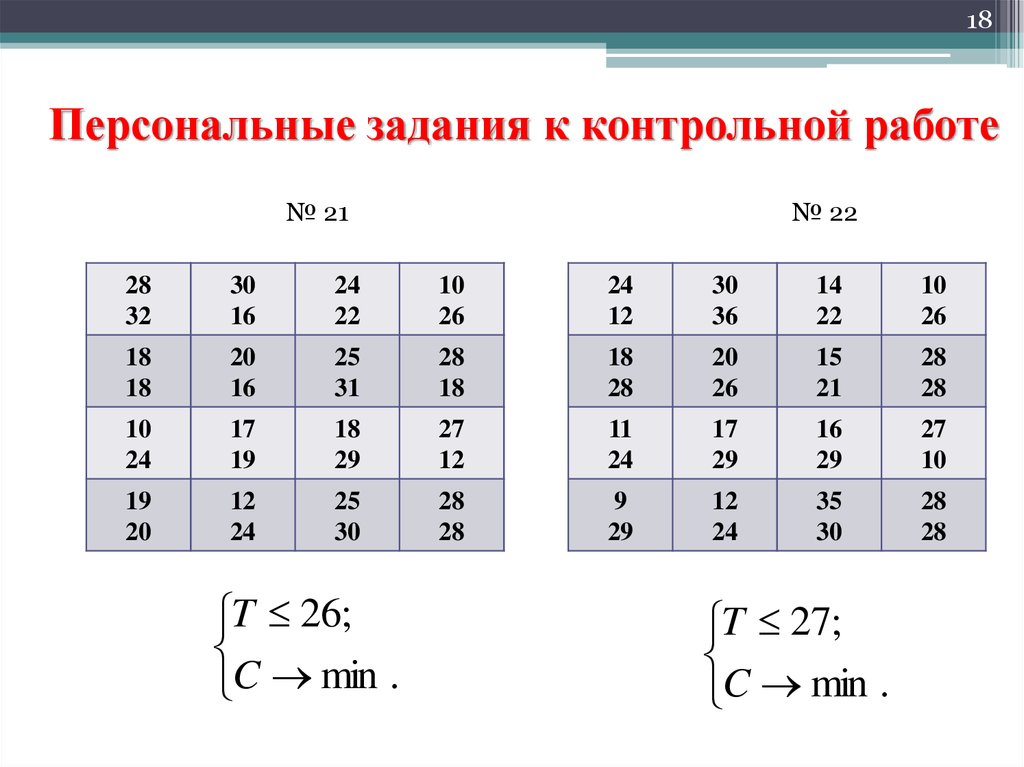
18. Персональные задания к контрольной работе

18
Персональные задания к контрольной работе
№ 21
№ 22
28
32
30
16
24
22
10
26
24
12
30
36
14
22
10
26
18
18
20
16
25
31
28
18
18
28
20
26
15
21
28
28
10
24
17
19
18
29
27
12
11
24
17
29
16
29
27
10
19
20
12
24
25
30
28
28
9
29
12
24
35
30
28
28
T 26;
C min .
T 27;
C min .

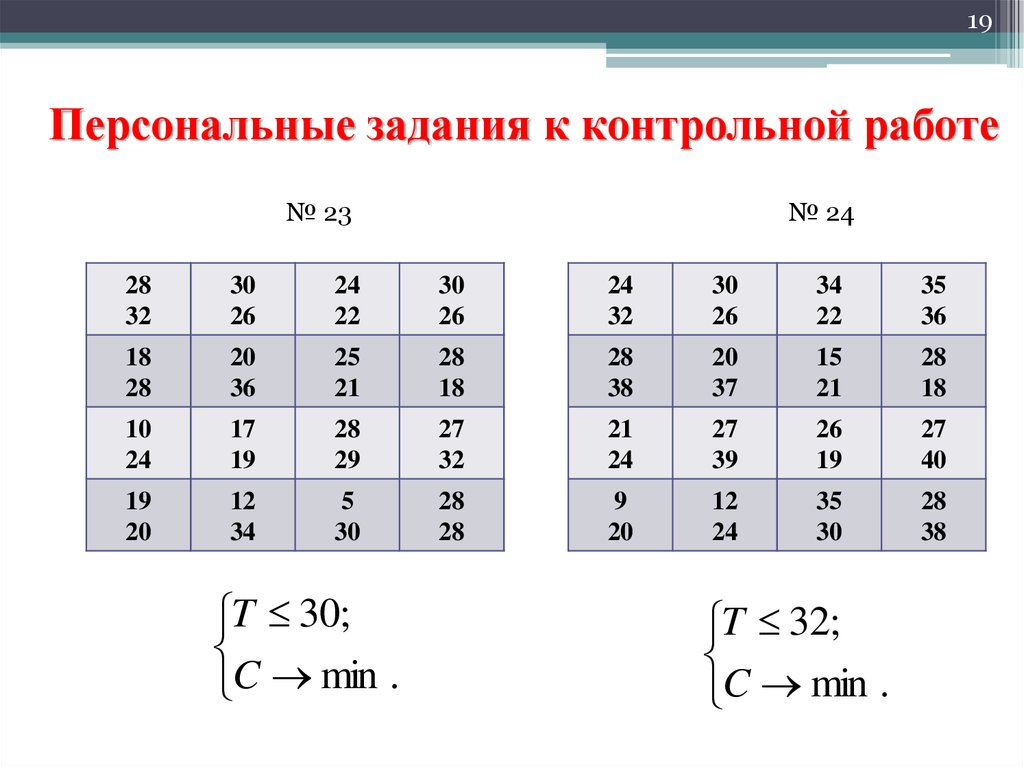
19. Персональные задания к контрольной работе

19
Персональные задания к контрольной работе
№ 23
№ 24
28
32
30
26
24
22
30
26
24
32
30
26
34
22
35
36
18
28
20
36
25
21
28
18
28
38
20
37
15
21
28
18
10
24
17
19
28
29
27
32
21
24
27
39
26
19
27
40
19
20
12
34
5
30
28
28
9
20
12
24
35
30
28
38
T 30;
C min .
T 32;
C min .

20. ЗАДАЧА 2: Минимизация времени выполнения плана при ограничениях на затраты

20
ЗАДАЧА 2: Минимизация времени
выполнения плана при
ограничениях на затраты
Пусть С – верхняя граница затрат на выполнение
плана. Остальные обозначения совпадают с
принятыми для задачи 1. Требуется таким образом
распределить работу между исполнителями, чтобы:
а) суммарные затраты не превысили величины С;
б) все исполнители были заняты;
в) все работы были выполнены;
г) время выполнения работ должно быть
минимально.

21. ФОРМАЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ 2

21
ФОРМАЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ 2
max max r2 (i, j ) y (i, j ) min; - целевая функция
j
i
n n
r1 (i, j ) y (i, j ) C ; - ограничение на суммарные затраты
i 1 j 1
n
y (i, j ) 1; j 1,2,..., n; - каждая работа должна быть выполнена
i 1
n
y (i, j ) 1; i 1,2,..., n; - каждый рабочий должен быть занят
j 1
y (i, j ) 1,0; i 1,2,..., n; j 1,2,..., n.

22. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ 2

r2 (i, j ) k r2 (i, j ) k 1 , где k 2,3,..., q 1; q число дуг графа
22
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ 2
Решение задачи 2 сводится к многократному решению
«классической» задачи о назначениях, для чего можно
воспользоваться следующим алгоритмом:
Шаг 1. Из исходного графа удаляются все ребра.
Шаг 2. Ищется такое упорядочение ребер (i, j )1 , (i, j ) 2 ,..., (i, j ) q ,
для которого справедливо:
r2 (i, j ) k r2 (i, j ) k 1 , где k 1,2,3,..., q 1; q число ребер графа.
Шаг 3. t = 1.
Шаг 4. В граф возвращаются первые t ребер упорядочения π.
Шаг 5. На полученном графе ищется решение «классической»
задачи о назначениях.

23. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ 2 (ПРОДОЛЖЕНИЕ)

23
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ 2
(ПРОДОЛЖЕНИЕ)
• Шаг 6. Если значение целевой функции
больше, чем С, то перейти к Шагу 7, нет – к
Шагу 10.
• Шаг 7. t = t + 1.
• Шаг 8. Если t<q+1, то перейти к Шагу 4, если же
t > q, - то к Шагу 9.
• Шаг 9. Печать «Нет решения», перейти к Шагу
11.
• Шаг 10. Время выполнения плана равно r2(i,j)t.
• Шаг 11. Конец алгоритма.

24. ПРИМЕР 2

24
ПРИМЕР 2
Решить задачу 2 для графа G(X, U) при С = 26. Исходные
данные представлены на рисунке и в таблице ниже.

25. ПРИМЕР 2 (продолжение)

25
ПРИМЕР 2 (продолжение)
• Перестановка π, полученная на шаге 2, имеет
вид: π= {(2,1); (3,3); (1,2); (2,2); (1,1); (2,3);
(3,2); (1,3); (3,1)} .

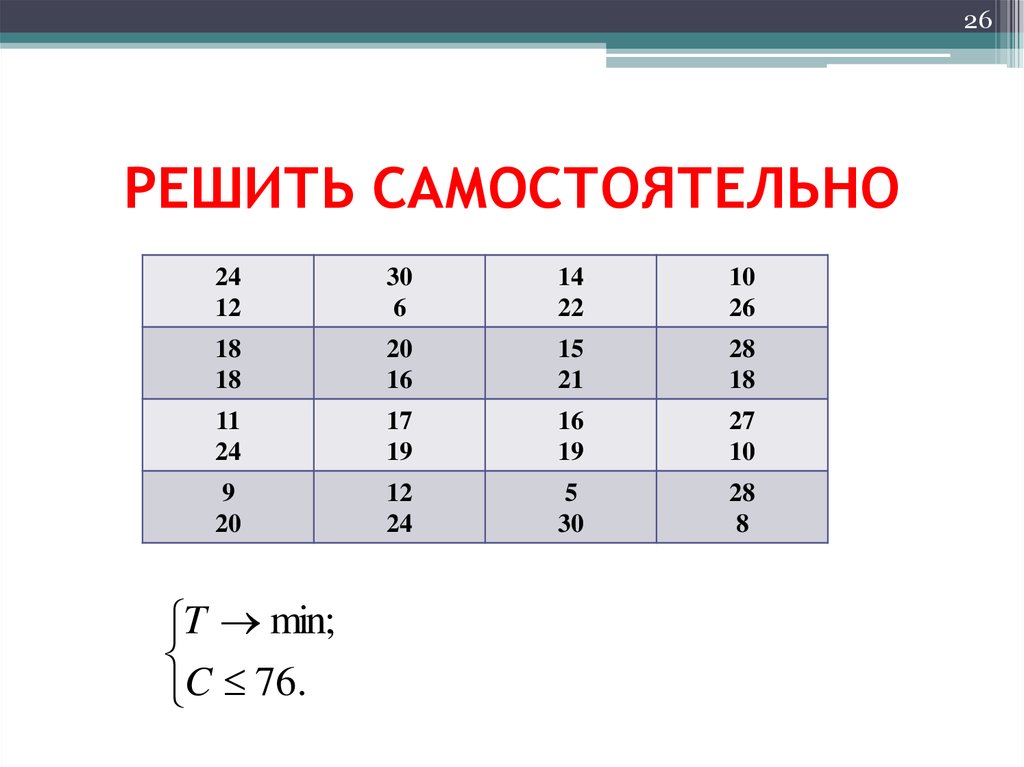
26. РЕШИТЬ САМОСТОЯТЕЛЬНО

26
РЕШИТЬ САМОСТОЯТЕЛЬНО
24
12
30
6
14
22
10
26
18
18
20
16
15
21
28
18
11
24
17
19
16
19
27
10
9
20
12
24
5
30
28
8
T min;
C 76.

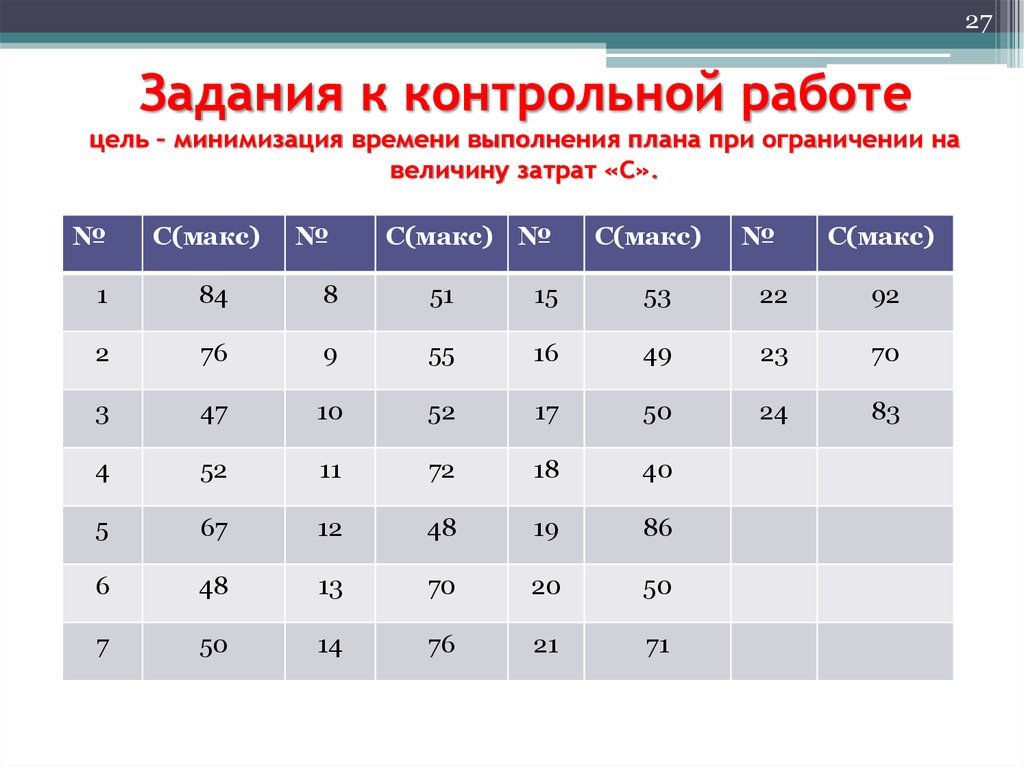
27. Задания к контрольной работе цель – минимизация времени выполнения плана при ограничении на величину затрат «С».

27
Задания к контрольной работе
цель – минимизация времени выполнения плана при ограничении на
величину затрат «С».
№
С(макс)
№
С(макс) №
С(макс)
№
С(макс)
1
84
8
51
15
53
22
92
2
76
9
55
16
49
23
70
3
47
10
52
17
50
24
83
4
52
11
72
18
40
5
67
12
48
19
86
6
48
13
70
20
50
7
50
14
76
21
71