Электромагнитные гармонические колебания и их математическое обоснование

1. «Самая лучшая физика – это хорошая математика».

«Самая лучшая физика – эт о хорошая
мат емат ика».
«Элект ромагнит ные гармонические
колебания и их мат емат ическое
обоснование».
Урок изучения нового мат ериала,
инт егрированный урок: физика и
мат емат ика.
СПБ ГБПОУ «Колледж «Красносельский"
Выполнил(а) учащиеся группы 11 РМ
Проверил преподават ель по мат емат ики:
Викулина Е.В.

2.

Цель учебная:
Сформировать у студентов понятие «гармоническое
колебание» и научить определять параметры колебаний
математическими способами.
Задачи урока:
1. Показать аналогию между параметрами, характеризующими
механические и электромагнитные колебания.
2. Раскрыть сущность определения параметров по уравнениям
гармонических колебаний и их графикам.
3. Раскрыть принцип построения графиков гармонических
колебаний по их уравнениям.
Развивающая цель:
Показать студентам роль межпредметных связей при
изучении курсов математики и физики; раскрыть сущность
аналогии как метода научного познания.
Воспитательная цель:
Воспитания устойчивого интереса студентов к достижению
результатов своей работы.

3. Формы и методы обучения

• беседа;
рассказ;
объяснит ельно-иллюст рационный:
проблемные сит уации:
мет од суждения.

4. Структура занятия:

Акт уализация знаний.
Мот ивация учебной деят ельност и.
Пост ановка цели.
Формирование новых знаний.
Конт роль полученных знаний.
Подведение ит огов.

5. Актуализация раннее усвоенных знаний.

Акт уализация раннее усвоенных знаний.
• Преподаватель физики задает вопросы
студентам:
• Чт о собой предст авляют колебания?
• В каких разделах физики мы о них
говорили? Приведит е примеры.
• Студенты отвечают на поставленные вопросы

6. Аналогия между механическими и электромагнитными колебаниями.

-Какие условия необходимо создат ь для получения
механических колебаний?
-Как получают элект ромагнит ные колебания?
Аналогия между механическими и элект ромагнит ными
колебаниями.

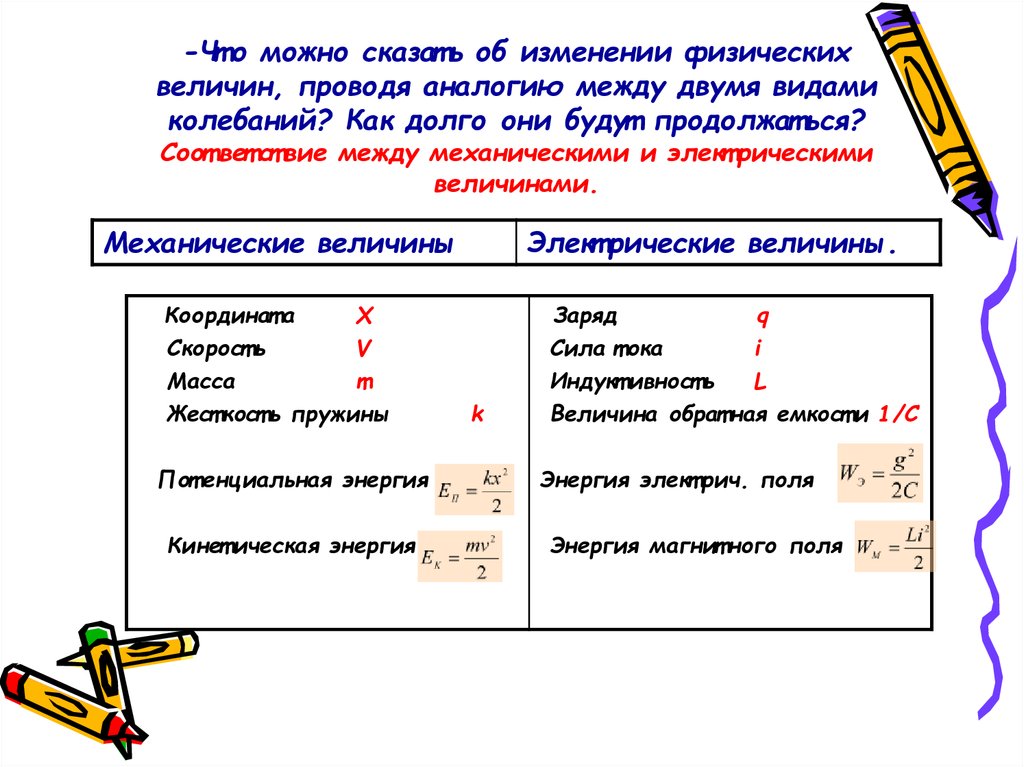
7. -Что можно сказать об изменении физических величин, проводя аналогию между двумя видами колебаний? Как долго они будут продолжаться? Соотв

-Чт о можно сказат ь об изменении физических
величин, проводя аналогию между двумя видами
колебаний? Как долго они будут продолжат ься?
Соот вет ст вие между механическими и элект рическими
величинами.
Механические величины
Координат а
Х
Скорост ь
V
Масса
m
Жест кост ь пружины
Пот енциальная энергия
Кинет ическая энергия
Элект рические величины.
k
Заряд
q
Сила т ока
i
Индукт ивност ь
L
Величина обрат ная емкост и 1/С
Энергия элект рич. поля
Энергия магнит ного поля

8. Мотивация учебной деятельности

• Преподаватель физики отмечает, что колебания
свойственны всем явлениям природы: пульсируют
звезды, вращаются планеты, внутри организма бьется
сердце и т. д. Вам известна природа возникновения
механических и электромагнитных колебаний.
• Вопрос: Как вы думает е, какими же
парамет рами будут характ еризоват ься
рассмот ренные нами колебат ельные
процессы?
• (Студенты правильного ответа на вопрос не
дают, т.к. у них не хватает знаний)

9. Постановка цели урока

Пост ановка цели урока
• Правильно ответить на поставленный вопрос
вам поможет изучение явлений
«гармонические колебания в физике».
Изучение данного явления невозможно без
знаний, полученных из курса математики.
Сегодня вам предстоит познакомиться:
• во –первых, с основными понят иями и
терминами т еории колебания;
• во–вт орых, с мат емат ическими
соот ношениями, описывающими колебания.
• И первое, и второе очень важно для понимания
всего последующего курса физики.

10. Изучение нового материала.

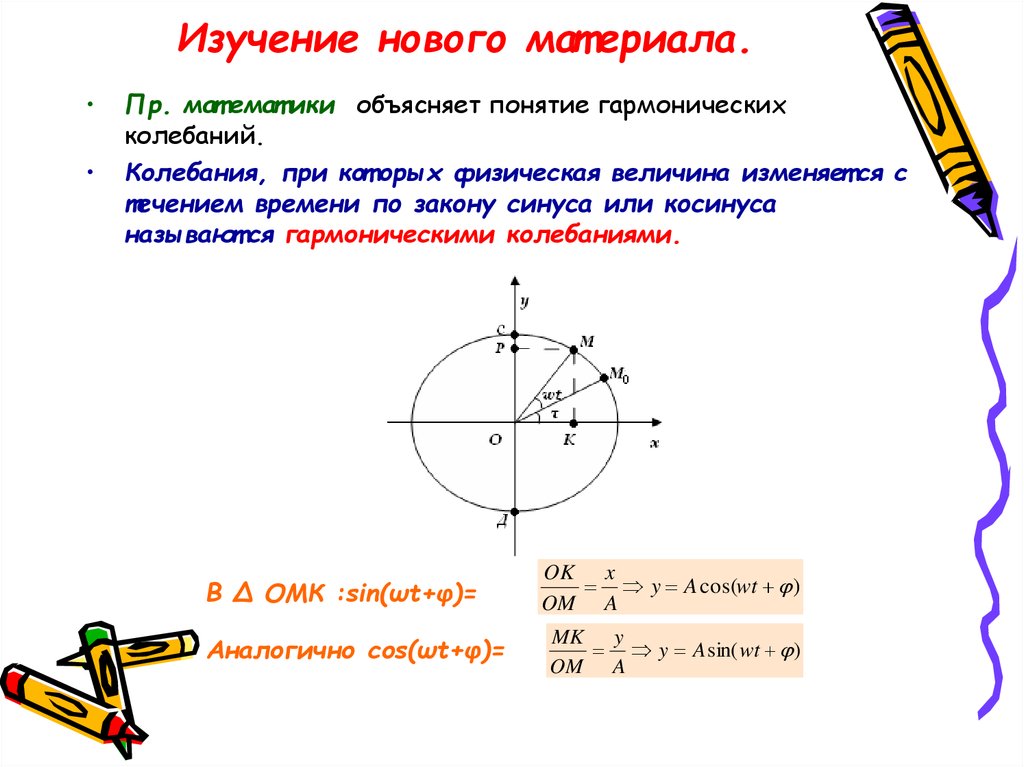
Изучение нового мат ериала.
Пр. мат емат ики объясняет понятие гармонических
колебаний.
Колебания, при кот орых физическая величина изменяет ся с
течением времени по закону синуса или косинуса
называют ся гармоническими колебаниями.
В ∆ ОМК :sin(ωt+φ)=
Аналогично cos(ωt+φ)=
OK x
y A cos(wt )
OM A
MK y
y A sin( wt )
OM A

11. Графически гармонические колебания изображаются синусоидами График синусоиды.

Графически гармонические колебания
изображают ся синусоидами
График
синусоиды.

12.

• Пр. физики предлагает студентам
объяснить :
• «Почему колебания груза на
пружине и свободные колебания в
закрытом контуре можно
представить с помощью
гармонического закона косинуса?»

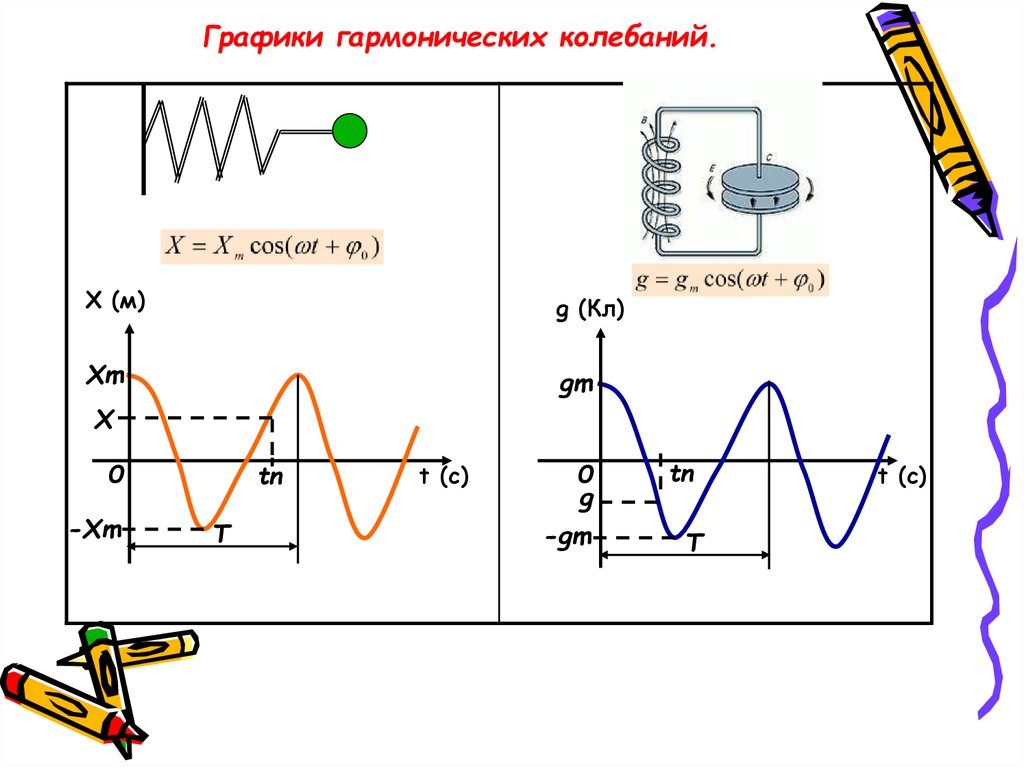
13. Графики гармонических колебаний.

Х (м)
g (Кл)
Хm
gm
Х
0
-Хm
tn
Т
t (c)
0
g
-gm
tn
Т
t (c)

14. Пр. математики, используя уравнения гармонических колебаний и их графики, вводит понятие гармонических колебаний. , Параметры гармоническ

Пр. мат емат ики, используя уравнения гармонических
колебаний и их графики, вводит понятие гармонических
колебаний.
, Парамет ры гармонических колебаний.
• 1. Модуль наибольшего значения колеблющейся
величины называет ся амплит удным значением.
Хm(м) – амплит уда механического колебания;
gm(Кл) – амплит уда заряда конденсат ора;
Im(A) – амплит уда силы т ока;
Um(B) – амплит уда напряжения .
• 2. Значение колеблющейся величины в любой
момент времени называет ся мгновенным значением.
Хm(м) – амплит уда механического колебания;
gm(Кл) – амплит уда заряда конденсат ора;
Im(A) – амплит уда силы т ока;
Um(B) – амплит уда напряжения

15. Первичная проверка понимания и обсуждение результатов.

Первичная проверка понимания и обсуждение результ ат ов.
• Задание №1.
Указать моменты времени, когда значение колеблющихся
величин на представленных графиках приобретают:
А). Амплитудные значения.
Б). Мгновенные значения.
g (Кл)
Х (м)
0
2
6
9 12 16
Рис.1 График механического
колебания.
t (c)
0
2 3
7
10
t (c)
Рис.2 График электромагнитного
колебания.

16. Изучение нового материала. Параметры гармонических колебаний.

Изучение нового мат ериала.
Парамет ры гармонических колебаний.
Пр. мат емат ики:
3. Минимальный промежут ок времени, в т ечении кот орого
значение колеблющейся величины полност ью повт оряет ся
называет ся периодом колебания.
Т (с) – период колебания.
Пр. физики :
Период собст венных незат ухающих колебаний конт ура, когда
его сопрот ивление равно нулю, определяет ся по формуле
английского физика Томсона:
T 2 LC
Период колебаний в реальном конт уре напрямую зависит
от его сопрот ивления R. Чем больше сопрот ивление R
закрыт ого колебат ельного конт ура, т ем больше период его
колебаний.

17. Параметры гармонических колебаний.

Парамет ры гармонических колебаний.
• Пр. мат емат ики:
• 4. Величина обрат ная периоду называет ся част от ой
колебания.
Герц, Гц - част от а колебания.
1
Т
Пр. физики:
• Част от у свободных колебаний, возникающих в замкнут ом
колебат ельном конт уре, называют собст венной част от ой
колебат ельной сист емы.
• Част от а собст венных незат ухающих колебаний конт ура
вычисляет ся по формуле:
1
2 LC

18. Первичная проверка понимания и обсуждение результата.

Первичная проверка понимания и обсуждение результ ат а.
• Задание №2.
Указать периоды колебаний на представленных
графиках и рассчитать частоты колебания.
Х (м)
0
g (Кл)
t (c)
Т1
0
2 4 6 8 10 12 14 t (c)
Т2
Т3
Т4
Рис.1 График механического
колебания.
Рис.2 График электромагнитного
колебания.

19. Изучение нового материала.

Изучение нового мат ериала.
Пр. мат емат ики: Из курса мат емат ики извест но, чт о
наименьшим периодом функции косинуса и синуса
являет ся величина 2П.
• 5. Если рассмат риват ь число колебаний не за 1с, а за
2Пс, т о полученную част от у называют циклической или
круговой част от ой.
2
2
Т
рад. с
- циклическая или круговая част от а колебаний
Пр. физики:Циклическая част от а колебаний для
закрыт ого колебат ельного конт ура вычисляет ся по
формуле:
1
LC

20. Пр. математики:

Пр. мат емат ики:
• 6. Выражениение, кот орое ст оит под знаком синуса или
косинуса в уравнении гармонического колебания,
называет ся фазой колебания.
• φ [рад]- фаза колебания
• Значение фазы в момент времени, равной нулю,
называют начальной фазой колебания.
φ0 [рад] – начальная фаза колебания.
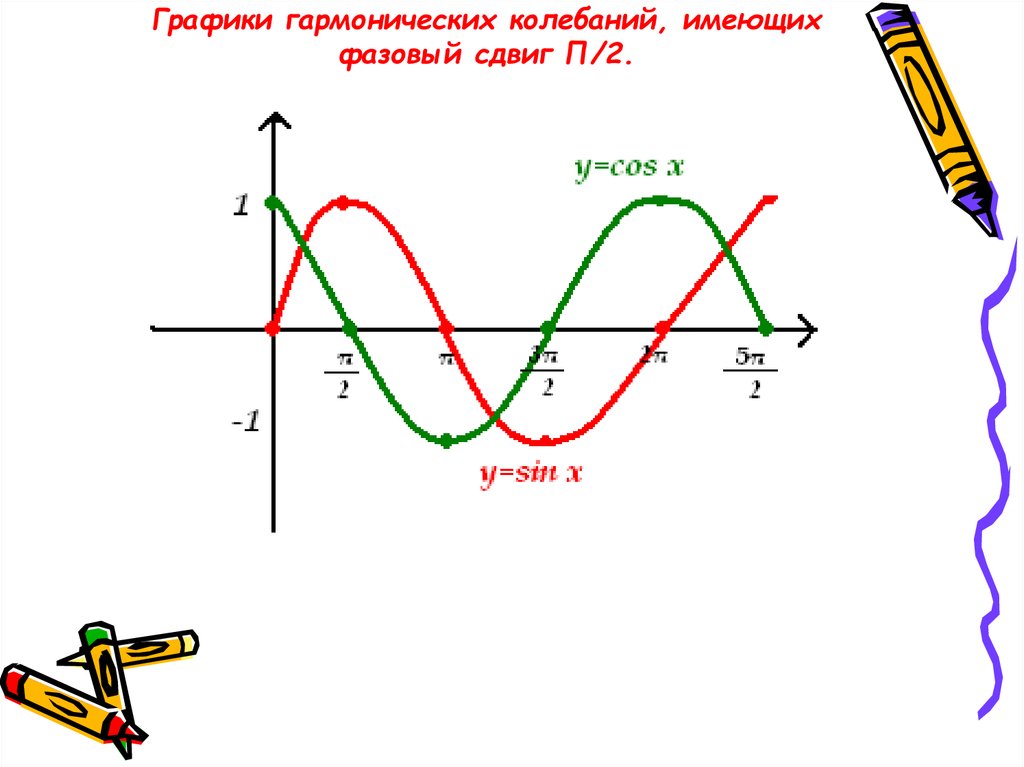
Функции у = cosx и у=sinx от личают ся друг от друга
фазами колебаний
cosφ = sin(φ + π/2)
Разност ь между фазами колеблющихся величин
называют фазовым сдвигом.
∆φ = φ2 - φ1 [рад]
.

21. Пример расчета разности фаз.

Пример расчет а разност и фаз.
Уравнение изменения заряда конденсат ора по закону
косинуса:
cos t рад
Уравнение изменения заряда конденсат ора по закону
синуса:
sin ( t ) рад
2
Фазовый сдвиг между уравнениями:
sin cos ( t
2
t)
2
рад

22. Графики гармонических колебаний, имеющих фазовый сдвиг П/2.

23. Пр. математики.

Пр. мат емат ики.

24.

25. Подведение итогов занятия.

Подведение ит огов занят ия.
• Пр. физики.
• У ст удент ов сформировалось понят ие
элект ромагнит ного гармонического колебания, они
убедилась в наличии мат емат ического обоснования
данного процесса, уяснили сущност ь парамет ров
гармонических колебаний и способы вычисления их
мат емат ическим и физическим пут ем , они смогли
полученные знания использовали при выполнении
проверочного задания. Запись конспект а занят ия
проводилась в рабочие т ет ради ст удент ов, они
проявляли инициат иву при работ е, т ак как
заинт ересованы в ее результ ат ах.