Тепломассообмен. Вынужденная конвекция

1. Тепломассообмен 12

Вынужденная конвекция

2. Моделирование процессов конвективного теплообмена

После проектирования и перед изготовлением энергетической
установки ее работу проверяют на модели, потом делают
опытный экземпляр. Чтобы можно было перенести результаты
испытаний на модели на натурную установку, надо выдержать
условия подобия: геометрические, физические, граничные.
Для геометрического подобия модель должна быть точной
копией натуры в масштабе
c мод / нат .
Для физического подобия
нат c мод; нат c мод .
необходимо условие
Подобие граничных условий выдержать сложно, поэтому
ограничиваются соблюдением условий подобия на входе
жидкости в модель и натуру, то есть определяющие числа
подобия на входе должны быть равными.

3. Условия моделирования процессов

Reн wн
wм
Re м
Значит скорость жидкости на входе
н
м
в модель должна быть:
Если жидкость одна и та же, то м / н 1 ,
wм wн н м .
то есть при
/ м 10 wм 10wн .
м н
н
Необходимо также равенство чисел Прандтля Prм Prн .
Для разных жидкостей это трудно выдержать, например,
Prвод Prвозд при :tвод 150...3000 C, что соответствует давлению
насыщения воды p 5 . Если учитывать еще и влияние
н
температуры на физические свойства жидкости, то точное
моделирование обеспечить сложно. Поэтому прибегают к
методам приближенного моделирования, например, используют
автомодельность (независимость) процесса от какого то
критерия. Тогда его влияние на процесс не учитывается.
н
м

4. «Вырождение» критериев подобия

Число Рейнольдса – это соотношение сил инерции и трения.
Если одна из этих сил бесконечно велика или мала, то число
Рейнольдса очень большое или очень малое, то есть
происходит его «вырождение» – оно выпадает из числа
определяющих критериев подобия.
Например, при рассмотрении дифференциального уравнения
движения Навье-Стокса мы считали жидкость несжимаемой.
Но из
0 следует, что 0 (1 ) и в уравнении
0 движения должен быть член g 0 g 0 g ,
но он был упрощен ( g 0). Если же не упрощать, то кроме
0
числа Грасгофа появится еще критерий Галилея
g 30
Ga 2 ,
то есть при выводе уравнения движения мы
считали его вырожденным.

5. Обработка и обобщение результатов экспериментов

Часто вместо точного используется локальное моделирование.
Например, при поперечном обтекании трубного пучка ставится
только одна рабочая трубка (
калориметр), остальные
просто имитируют гидродинамику процесса. Это упрощает
моделирование и дает достаточно точные результаты.
Во время эксперимента должны быть измерены все величины,
входящие в числа подобия: тепловой поток, коэффициент
теплоотдачи, температуры жидкости и стенки, скорость жидкости.
При определении среднего по поверхности коэффициента
теплоотдачи из уравнения подобия можно исключить координаты.
Тогда зависимость примет вид:
Nu f (Re,Gr,Pr).
(1)

6. Измерение средних температур стенки и жидкости

бок (tc )
верх
низ
t
tж

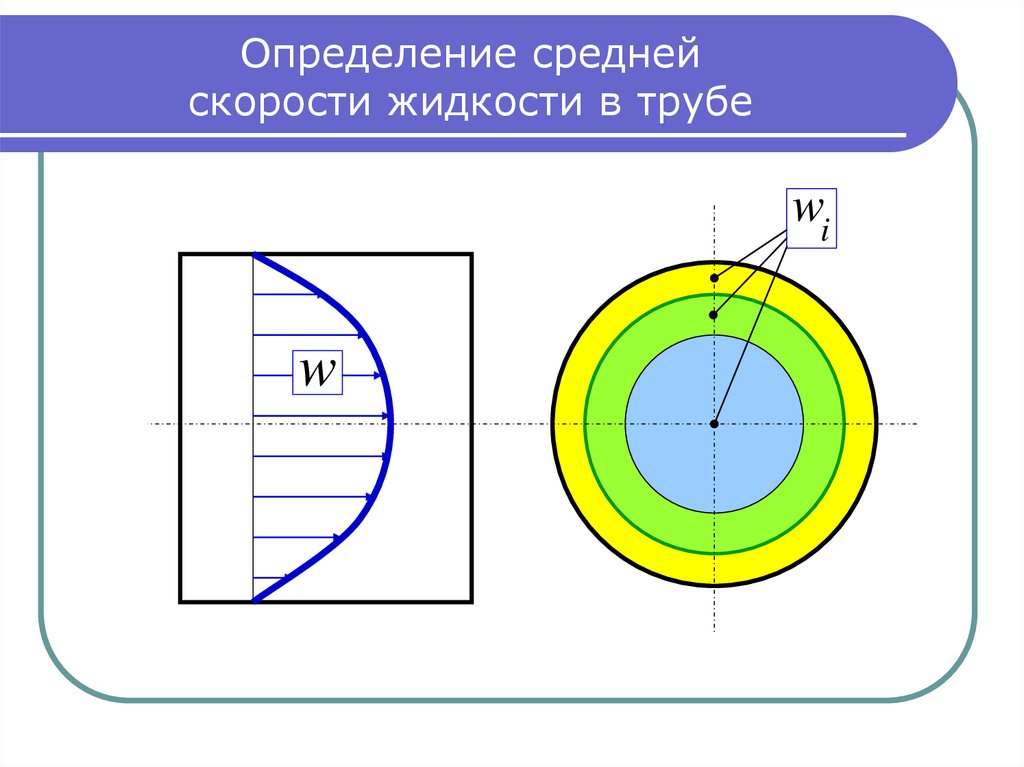
7. Определение средней скорости жидкости в трубе

wi
w

8. Уравнения подобия для вынужденной конвекции

С помощью трубки Пито в равновеликих сечениях f1 f 2 f 3
измеряются динамические напоры потока, по которым находятся
скорости жидкости в этих сечениях w 2 pд / . Тогда средняя
i
скорость жидкости в трубе равна средне-арифметической:
n
Для вынужденной конвекции число Грасгофа не
wж wi / n.
является определяющим, то есть вместо
1
уравнения (1) будет выражение Nu f (Re,Pr).
(2)
Обычно это степенная зависимость Nu c Rem Pr n .
(3)
Для одной жидкости, без учета влияния температуры,
можно считать Pr Const, то есть Nu c Rem ,
(4)
или в логарифмических координатах gNu gc m g Re.
(5)
Таким образом, выражение (5) представляет собой уравнение
прямой линии (см. следующий слайд).

9. Экспериментальное определение постоянных «с» и «m»

gNu
Nu c Rem
0
gc
*
*
m tg
*
*
* *
g Re

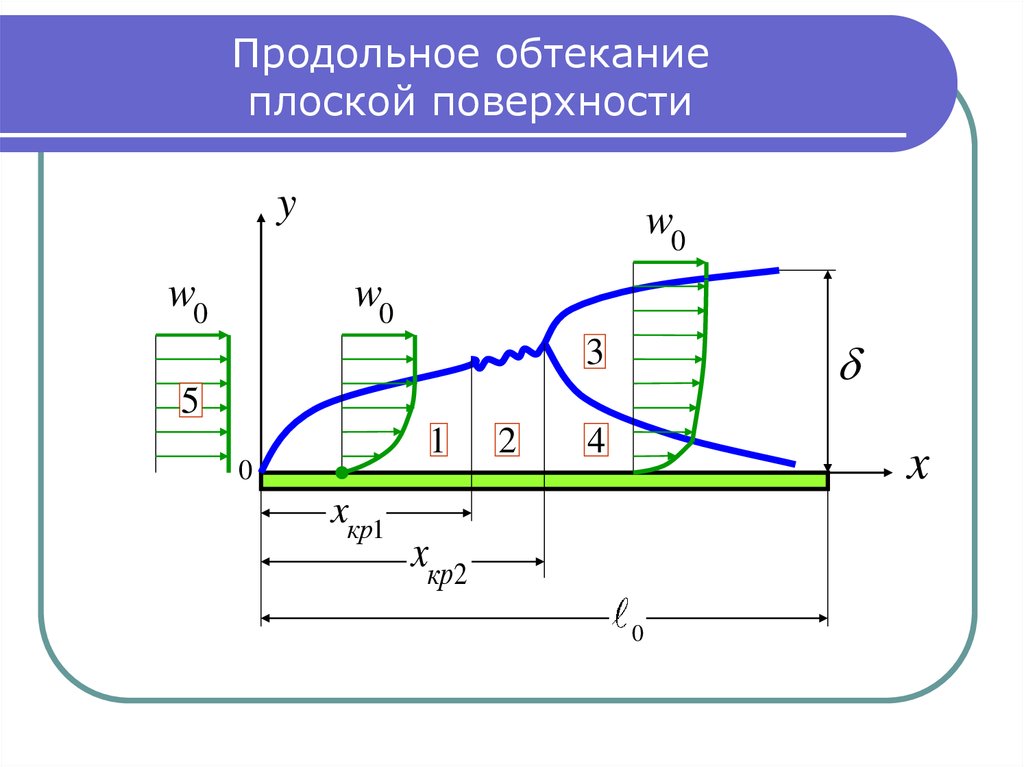
10. Продольное обтекание плоской поверхности

y
w0
w0
w0
3
5
1
0
xкр1
2
4
x
xкр2
0

11. Теплоотдача при продольном обтекании горизонтальной поверхности

1 – ламинарный пограничный слой; 2 – переходный режим;
3 – турбулентный пограничный слой; 4 – ламинарный
подслой; 5 - невозмущенная жидкость.
Обычно для простоты принимают xкр1 xкр2 xкр .
Тогда критическое значение числа Рейнольдса для перехода
от ламинарного пограничного
слоя к турбулентному:
Reкр
w0 xкр
.
(1)
В ламинарном пограничном слое скорость жидкости
изменяется по закону
wx
y
y
1,5( ) 0,5( )3,
кубической параболы:
w0
где толщина гидродинамического 4,64
.
пограничного слоя:
x Re x
(2)
(3)

12. Соотношение между толщинами пограничных слоев

Внутри ламинарного пограничного слоя движение жидкости
слоистое, перемешивания нет, поэтому теплота передается только
теплопроводностью, в этом случае распределение температур в
тепловом пограничном слое аналогично распределению скоростей
в гидродинамическом пограничном слое:
где k – толщина теплового
k
пограничного слоя:
Для газов Pr ≈ 1, поэтому k =
Подставив
1
.
3
Pr (5)
y
y
1,5( ) 0,5( )3, (4)
0
k
k
.
из (3) в (5), получим
толщину теплового пограничного слоя:
k
4,64x
.
3
Re x Pr
(6)
При постоянной температуре плоскости локальный коэффициент
теплоотдачи можно найти по уравнению подобия Михеева:

13. Уравнения подобия для теплоотдачи в ламинарном пограничном слое

0,33 (
Nuж, x 0,33Re0,5
Pr
ж, x
ж
где
Prж 0,25
) ,
Prc
(7)
tж средняя температура жидкости;
х – характерный линейный размер.
Если температура поверхности переменная. Обычно это
степенная зависимость вида:
c Axm ,
(8)
где А и m – постоянные, независимые от х.
Для этого случая справедливо критериальное уравнение:
0,33 (
Nuж, x 0,33 Re0,5
Pr
ж, x
ж
Поправки
Prж 0,25
) .
Prc
на переменную температуру поверхности
приведены на следующем слайде.
(9)

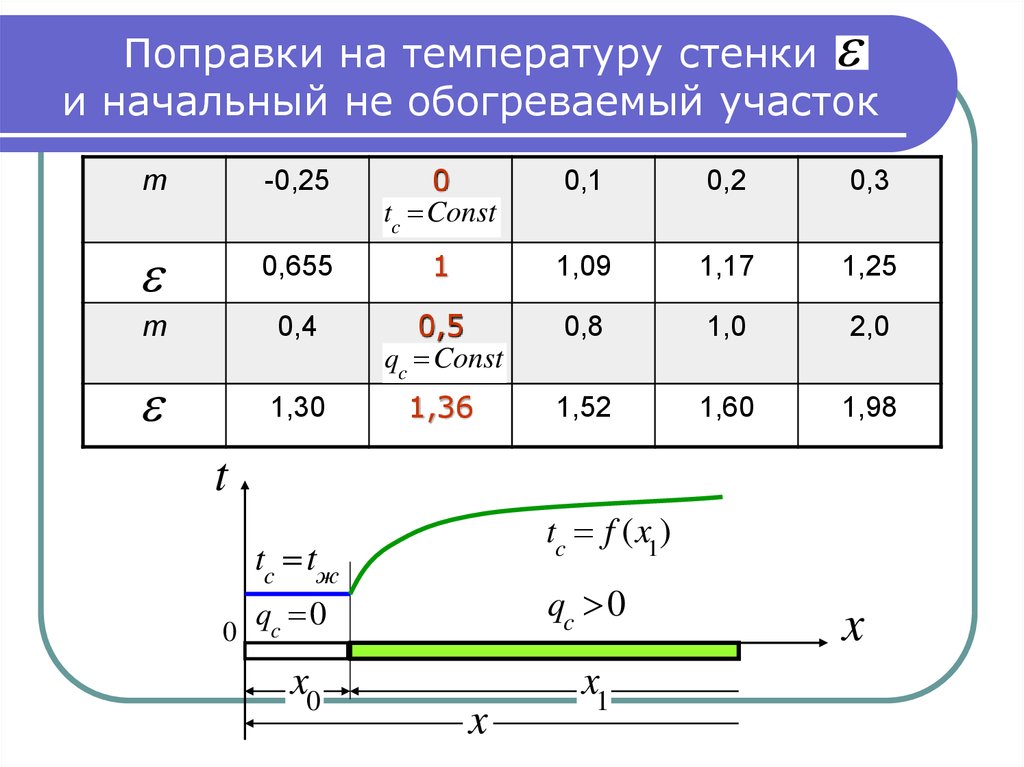
14. Поправки на температуру стенки и начальный не обогреваемый участок

m
-0,25
0,1
0,2
0,3
0
tc Const
0,655
1
1,09
1,17
1,25
m
0,4
0,8
1,0
2,0
0,5
qc Const
1,30
1,36
1,52
1,60
1,98
t
tc f ( x1)
tc tж
0
qc 0
qc 0
x0
x
x1
x

15. Уравнения подобия для теплоотдачи при продольном обтекании пластины

Если в начале плоскости есть не обогреваемый участок длиной
x0 , то уравнение подобия для этого случая имеет вид:
x
0,33 ( Prж )0,25.
Nuж, x 0,33 ( 1 )0,2 Re0,5
Pr
ж, x
ж
x
Prc
При
x0 0
(10)
x1
1,
x
формула (10) превращается в (9), а
при t Const - в (7).
c
Для турбулентного пограничного слоя
применимо уравнение подобия Михеева – Петухова:
0,43 ( Prж )0,25.
Nuж, x 0,0296Re0,8
Pr
ж, x
ж
Prc
На следующем слайде
представлено изменение
локального коэффициента теплоотдачи вдоль пластины.
(11)

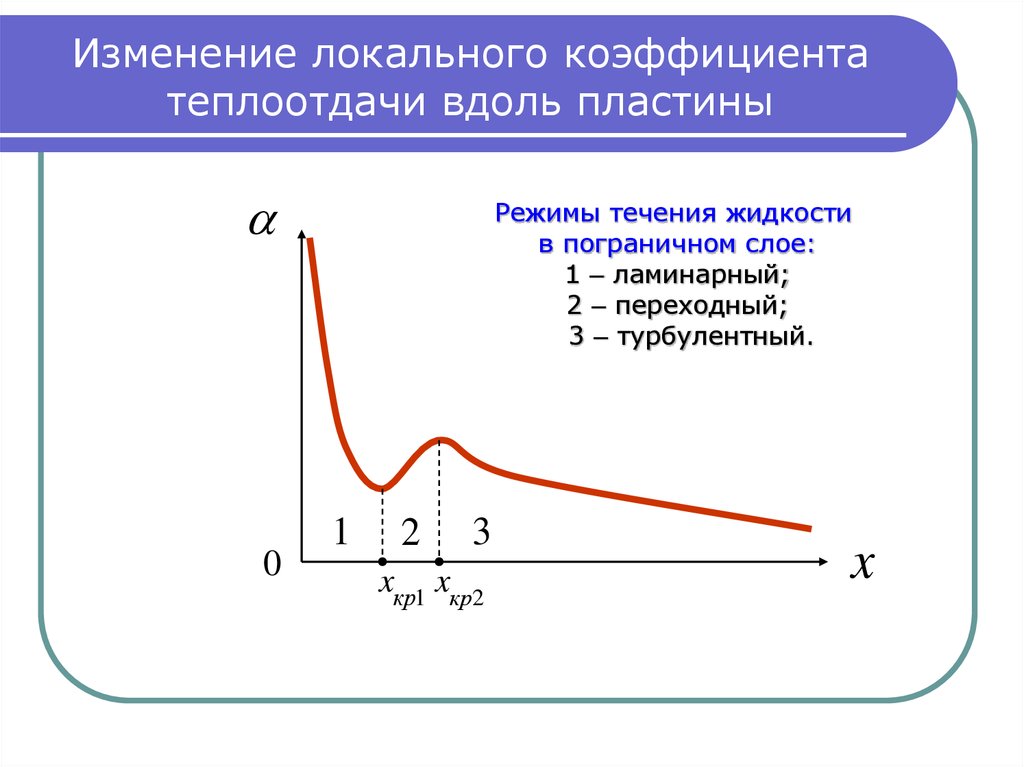
16. Изменение локального коэффициента теплоотдачи вдоль пластины

0
Режимы течения жидкости
в пограничном слое:
1 – ламинарный;
2 – переходный;
3 – турбулентный.
1
2
3
xкр1 xкр2
x