Similar presentations:
Девятая Всероссийская командная олимпиада школьников по программированию
1. Девятая Всероссийская командная олимпиада школьников по программированию
Разбор задач23 ноября 2008 года
Санкт-Петербург
2. A. Место у прохода, пожалуйста
Автор задачи – Андрей СтанкевичУсловие – Андрей Станкевич
Подготовка тестов – Владимир Ульянцев
Разбор – Владимир Ульянцев
3. Обозначения
n – количество креселl – длина салона
w – ширина салона
x – длина кресла
y – ширина кресла
a – ширина прохода
4. Расположение кресел по длине
Максимальное количество кресел вряду rowSize = l / x
Случай rowSize = 0
5. Расположение кресел по ширине
Необходимое количество рядовrows = (n + rowSize - 1) / rowSize
Допустимое количество проходов
aisles = (w - rows * y) / a
Условие на количество проходов
6. Ответ на задачу
Расположение проходов посленечетных рядов
2 * aisles * rowSize – максимальное
количество кресел, которое можно
поставить у прохода
Ответ - min(n, 2 * aisles * rowSize)
7. B. Мост
Автор задачи – Андрей СтанкевичУсловие – Андрей Станкевич
Подготовка тестов – Антон Феськов
Разбор – Антон Феськов
8. Река
Берега реки –ломаные, бесконечные
в обе стороны
Требуется построить
мост через реку
минимальной длины
9. Мост
Если ответ – L, то всегдасуществует мост длины L,
построенный через вершину
ломаной, образующей один из
берегов реки
Достаточно для каждой
вершины каждой ломаной
проверить расстояние до
каждого отрезка и луча второй
ломаной
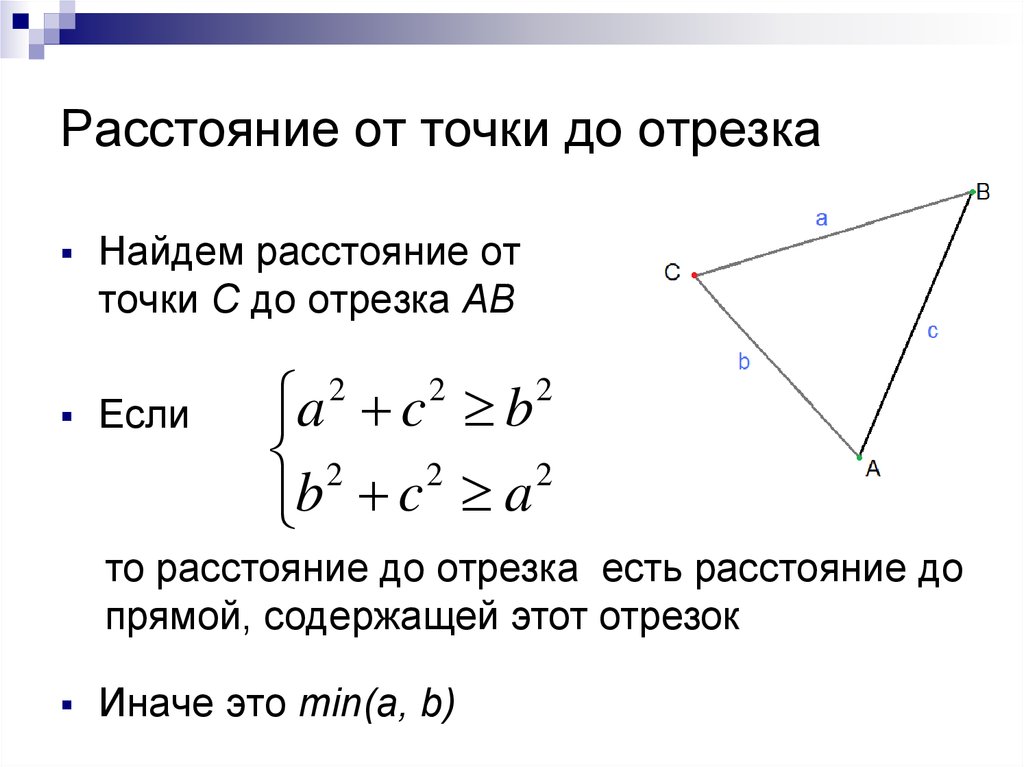
10. Расстояние от точки до отрезка
Найдем расстояние отточки C до отрезка AB
Если
a c b
2 2
2
b c a
2
2
2
то расстояние до отрезка есть расстояние до
прямой, содержащей этот отрезок
Иначе это min(a, b)
11. C. Почти беспрефиксные коды
Автор задачи – Антон ФеськовУсловие – Андрей Станкевич
Подготовка тестов – Сергей Поромов
Разбор – Сергей Поромов
12. Определение
Почти беспрефиксный код уровня k –набор слов, у которых наибольший
общий префикс имеет длину не более k
13. Решение с сортировкой
Отсортируемвсе
строки
в
лексикографическом порядке
Будем добавлять в искомый набор
слово, если его общий префикс с
предыдущим не превышает по длине k
14. Решение бором
Добавим все слова в борБудем
выводить
всевозможными
способами префиксы длины (k+1),
далее только одно их продолжение
Требует много памяти
15. Пример бора
Для строк: aaa, aab, ac, ba, bb, ca16. Решение хешами
Вычислим значения хеш-функции дляпрефиксов длины (k+1) всех строк
Отсортируем значения хеш-функции
Для каждого значения хеш-функции
выведем одного представителя
17. D. Обход в глубину
Автор задачи – Елена Андреева, ВикторМатюхин
Условие – Андрей Станкевич
Подготовка тестов – Олег Давыдов
Разбор – Антон Феськов
18. Исходный код
Если функция dfs вызвана для вершиныu, то среди программа находит
минимальную по номеру непосещенную
вершину v, такую что в графе есть ребро
(u, v) и вызывает dfs(v)
19. Будем называть:
Непосещенныевершины – белыми
Полностью
обработанные
вершины – черными
Те вершины, которые
находятся в стеке
вызовов (остальные) –
серыми
20. Если мы в вершине v:
В черные вершины нетдополнительных ребер
Ребро (u, v) можно
добавить только если
w<v
Рассмотрены все пары
вершин
21. E. Драгоценные камни
Автор задачи – Федор ЦаревУсловие – Федор Царев
Подготовка тестов – Антон Феськов
Разбор – Антон Феськов
22. Какие пары считать?
Строка SОпределены упорядоченные пары типов
камней: (a1, b1), (a2, b2), . . . , (ak, bk)
Найти количество пар индексов (i, j)
таких что 1 ≤ i < j ≤ n и существует такое
число q (1 ≤ q ≤ k), что Si = aq и Sj = bq
23. Как решать?
Представим пары таблицей логического типаM[a,b] = true если пара (a, b) красивая и false
иначе
Прибавляем по символу в конец текущей
строки. Храним количество символов каждого
типа в текущей строке (cnt[c])
Пересчет: для j-го символа:
for c = ‘a’ .. ‘z’
if (M[c, Sj]) then inc(result, cnt[c]);
24. F. Интересные числа
Автор задачи – Федор ЦаревУсловие – Федор Царев
Подготовка тестов – Сергей Поромов
Разбор – Федор Царев
25. Какие числа интересны?
Число x является интересным, еслимаксимальная степень k, на которое x
делится, нечетна
110002 = 2410 делится на 8=23, но не
делится на 16=24
26. Легко найти
Количествоинтересных чисел,
не превышающих
некоторое число y
Принцип включенияисключения
f ( y)
y
c ( m) m
k
km y
( 1)
m 1
m 1
c(m)
27. Двоичный поиск
Необходимо найти минимальное y, чтоf(y)=n
Инвариант f(hi) ≥ n, f(low) < n
while (low + 1 < hi) {
long middle = (low + hi) / 2;
if (calc(middle, k) >= n) {
hi = middle;
} else {
low = middle;
}
}
out.println(hi);
28. Альтернативный подход
Строим число, подбирая цифры со старшихразрядов
f(L) – количество чисел длины L, в которых
первая и последняя цифры – не нули
f ( L) (k 1) k
2
L 2
29. Альтернативный подход
Определим длину искомого числаКоличество интересных чисел заданной
длины g(L)
При восстановлении важно хранить позицию
последней ненулевой цифры
g ( L)
2 l 1 L
f ( L 2l 1)
l 0
30. G. Оптимизация
Автор задачи – Сергей КопелиовичУсловие – Роман Сатюков
Подготовка тестов – Роман Сатюков
Разбор – Роман Сатюков
31. Обозначения
M – число частей проектаmi – время выполнения i-ой части
проекта
pi
– номер работника, которому
назначена i-ая часть проекта
wi – время выполнения всех работ,
назначенных
работнику
номер
pi
(i=1..M).
32. Критерий оптимизирующей операции
Каждуюоперацию
можно
задать
номерами частей проекта, которые
меняются местами – (i, j).
Пара (i, j) – оптимизирующая, если и
только если выполняются условия:
mi m j
w
m
w
m
i
i
j
j
33. Сведение к задаче о количестве инверсий в последовательности
Отсортируем части проекта в порядкевозрастания величины mi.
Пусть pi = –(wi – mi).
Тогда
надо
найти
количество
инверсий в полученном массиве p.
Эта задача решается за O(MlogM).
34. H. Шкафы
Автор задачи – Владимир ГуровицУсловие – Андрей Станкевич
Подготовка тестов – Федор Царев
Разбор – Федор Царев
35. Динамическое программирование
f(h) – максимальное число полок,находящихся не выше высоты h, которые
можно открыть
Интересных высот мало – рассматривать
высоты внутри полок нет смысла
f (h) max( f (h a) 1, f (h b) 1, f (h 1))
36. Жадный алгоритм
Из двух самых нижних полок разумновыдвинуть ту, которая ниже
Дальше – аналогично
37. I. Архимедова спираль
Автор задачи – Владимир УльянцевУсловие – Федор Царев
Подготовка тестов – Владимир Ульянцев
Разбор – Роман Сатюков
38. Уравнения движения
α(t) = ω∙tρ(t) = R + V∙t
x(t)= ρ(t) ∙ cos(α(t))
y(t)= ρ(t) ∙ sin(α(t))
x(t)= (R + V∙t) ∙ cos(ω∙t)
y(t)= (R + V∙t) ∙ sin(ω∙t)
Найти минимум и максимум каждой функции
при 0 ≤ t ≤ T
39. Преобразование уравнений
Несложными преобразованиями задачасводится к задаче поиска максимума
функции
f (t ) (a t ) cos(t )
при условии
t [tmin ; tmax ]
Замечание:
tmax – tmin<2
можно
считать
что
40. График f(t) при a=2
41. Варианты решения
1. Для поиска максимума выпуклойфункции можно применить тернарный
поиск.
2. Максимумы функции находятся в
корнях
ее
производной.
Корни
производной можно найти с помощью
двоичного поиска.
42. Варианты решения
3. Перебрать все t из диапазона [tmin;tmax]с некоторым шагом ε и найти значение
t1 с наибольшим значением f(t1). После
этого перебрать все t в некоторой
окрестности t1 с некоторым шагом ε2
(уточнить найденное t1).
43. Тернарный поиск
Задача: Дана функция f(t), выпуклаявверх на отрезке [a, b]. Требуется найти
её максимум.
Инвариант:
максимум
функции
достигается где-то на отрезке [a, b]
Разделим отрезок на три равные части:
[a, x1], [x1, x2], [x2, b].
44. Тернарный поиск
Возможны два случая:≤ f(x2)
f(x1) > f(x2)
f(x1)
В первом случае максимум не может
достигаться на отрезке [a, x1]. Переходим к
отрезку [x1, b].
Во втором случае максимум не может
достигаться на отрезке [x2, b]. Переходим к
отрезку [a, x2].
Длина отрезка [a, b] каждый раз уменьшается
в полтора раза.
45. Тернарный поиск: Код
while (a + ε < b) {double x1 = (2·a + b) / 3;
double x2 = (a + 2·b) / 3;
if (f(x1) ≤ f(x2))
a = x1;
else
b = x2;
}
46. J. Сумма
Автор задачи – Роман СатюковУсловие – Роман Сатюков
Подготовка тестов – Роман Сатюков
Разбор – Роман Сатюков
47.
Представим числа A, B и C в следующемвиде:
A 10 A
a
B 10 B
b
C 10 C
c
Числа A’, B’ и C’ не делятся на 10
Утверждение: Задача для чисел A, B, C
имеет решение задача для чисел A’, B’, C’
имеет решение
48.
Найдем натуральные x, y и z, такие что:A 10 B 10 C 10
x
y
z
Тогда исходная задача имеет решение:
b c x
A 10
B 10
a c y
C 10
a b z
49. Случай когда A,B,C не делятся на 10
A 10 B 10 C 10n
m
k
Можно считать, что не более двух чисел из
n, m, k больше нуля (если нет – уменьшим
n, m и k на единицу).
Утверждение: Максимум одно из чисел из
n, m, k больше нуля.
Получается три случая: n=m=0, n=k=0 и
m=k=0.
50.
Случай n=m=0:Получается
уравнение A+B=C·10k.
Поскольку числа A, B и C заданы в
десятичной системе исчисления, то найти
такое
k
можно
за
время,
пропорциональное числу цифр в числах A,
B, C.
Случай n=k=0:
Получается
уравнение A+B·10m=C, которое
преобразуется к уравнению C–A=B·10m.
Это уравнение аналогично уравнению,
полученному в случае n=m=0.
Случай m=k=0: Аналогично
предыдущему случаю.


















































 education
education








