Основы метода сетевого планирования и управления

1. Логистика

Тема: Основы метода сетевого
планирования и управления (СПУ)
КТН, доцент
Манкевич
Александр Валерьевич

2. Учебные вопросы:

1. Основные понятия
2. Принципы и правила построения
сетевой модели
3. Алгоритм разработки сетевой модели

3. Первый учебный вопрос:

Основные понятия

4. 1.1 Сущность и методы применения сетевого планирования и управления

Сетевое планирование и управление – графоаналитический метод, который опирается на теорию
графов.
Граф – множество вершин и соединяющих их дуг.
Сетевой график – схема на которой в строго
определённой технологической взаимосвязи наглядно
показаны все работы планируемого процесса от его
начала до полного его выполнения.

5. 1.1 Сущность и методы применения сетевого планирования и управления

Области применения:
планирование и осуществление строительных работ;
планирование трудовой деятельности;
составление бухгалтерских отчётов;
разработка торгового и финансового плана и т.д.
Достоинства метода:
концентрация внимания на важных работах;
установление
чёткой
взаимосвязи
между
исполнителями;
возможность
рационального
маневрирования
ресурсами;
экономия времени, средств и других ресурсов;
возможность алгоритмизации и решения на ЭВМ.

6. 1.2 Основные элементы сетевого графика

I. Работа
II. Событие
III.Путь
Работа - любой трудовой процесс или действие,
которое сопровождается затратами ресурсов и
времени. Обозначается
Пример:
Погрузка товара (А)
Оформление отчёта (Б)
6 чел., 3 маш.
2 чел., 7 дней
В понятие работа входят:
- ожидание
(пассивный
процесс,
когда
затрачивается только время);
- фиктивная работа (зависимость, когда нет затрат
ресурсов и времени). Обозначается

7. 1.2 Основные элементы сетевого графика

Событие – результат выполнения
нескольких предшествующих работ.
одной
или
Обозначается
Разновидности событий:
исходное событие (начало работы);
завершающее событие (конец работы).
Нумеруются целыми положительными числами от
исходного до завершающего в порядке возрастания.

8. 1.2 Основные элементы сетевого графика

Путь
–
событиями.
последовательность
работ
между
Разновидности:
полный путь (между исходным и завершающим
событиями);
критический путь (самый продолжительный из них).
Критическое время (ТКР) –
критического пути по времени.
продолжительность
Критические работы – работы, которые составляют
критический путь и не имеющие резервов времени
(узкие места сетевого графика). По опыту составляют
4-12% от общего числа работ.

9. Второй учебный вопрос:

Принципы и правила
построения сетевой модели

10. 2.1 Принципы

1. Принцип централизации (построение сверху вниз);
2. Принцип децентрализации (построение снизу вверх);
3. Комбинированный
вверх).
принцип
(сверху
вниз;
снизу
Принцип централизации используется в сетевых
графиках небольшого объёме (в строительстве, ремонт
цехов).
Принципы децентрализации и комбинированный
используется при сложных разработках в масштабах
отрасли или предприятия.

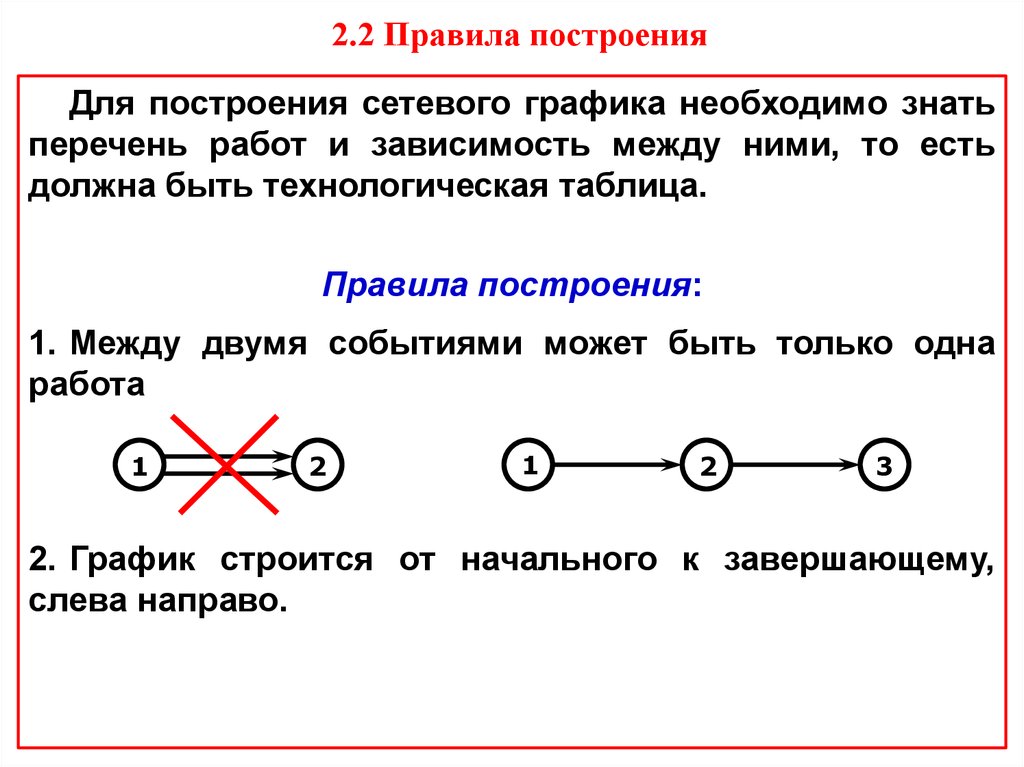
11. 2.2 Правила построения

Для построения сетевого графика необходимо знать
перечень работ и зависимость между ними, то есть
должна быть технологическая таблица.
Правила построения:
1. Между двумя событиями может быть только одна
работа
1
2
1
2
3
2. График строится от начального к завершающему,
слева направо.

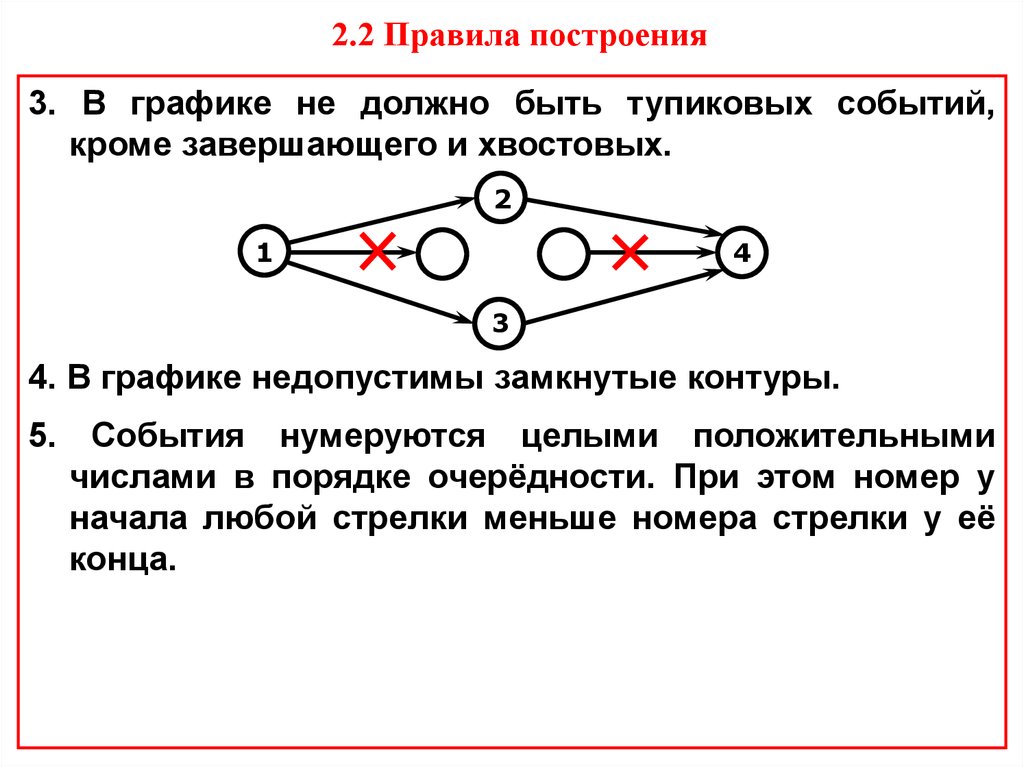
12. 2.2 Правила построения

3. В графике не должно быть тупиковых событий,
кроме завершающего и хвостовых.
2
1
4
3
4. В графике недопустимы замкнутые контуры.
5.
События нумеруются целыми положительными
числами в порядке очерёдности. При этом номер у
начала любой стрелки меньше номера стрелки у её
конца.

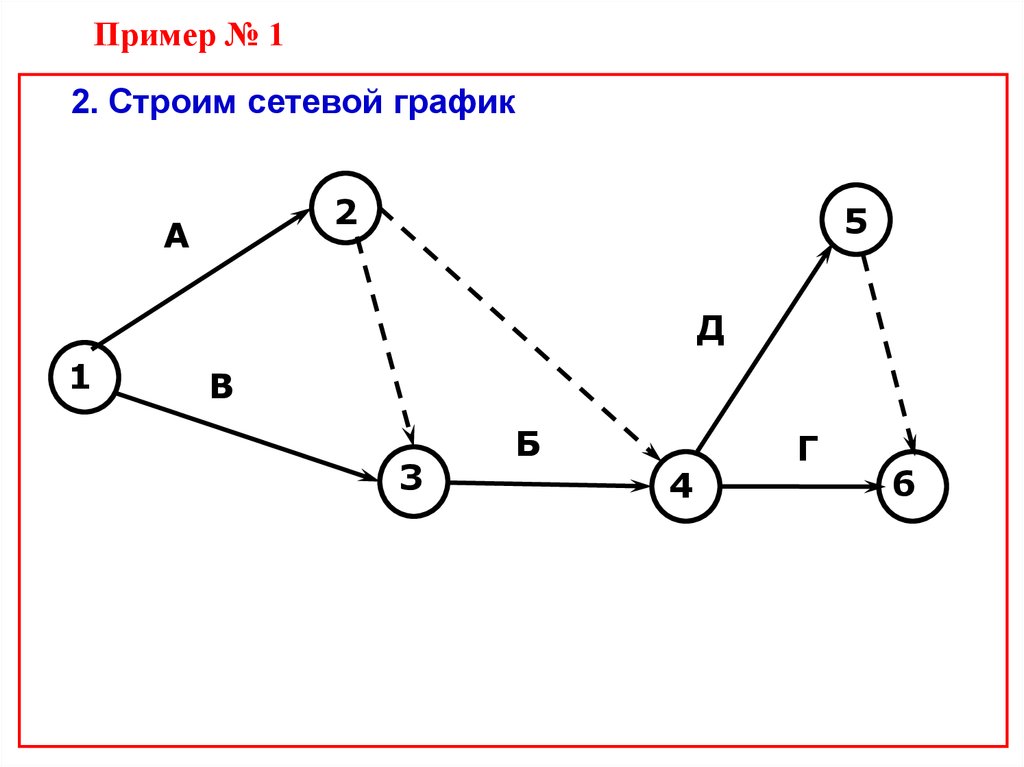
13. Пример № 1

Составить график из 5 работ: А; Б; В; Г; Д. Работы А
и
В
выполняются
параллельно,
после
чего
выполняется Б. Работы Г и Д выполняются
параллельно после выполнения работ А, Б.
1. Составляем технологическую таблицу
Предшествующие
работы
Последующие
работы
АВ
АБ
АБ
АВ
Б
Г
Д

14. Пример № 1

2. Строим сетевой график
2
А
5
Д
1
В
3
Б
4
Г
6

15. Третий учебный вопрос:

Алгоритм разработки сетевой
модели

16. 3.1 Основные этапы

1.
Составление
технологической
(расчленение процесса на отдельные
определение взаимосвязи)
таблицы
работы и
2. Определение продолжительности выполнения
работ и других числовых характеристик.
3. Составление исходного сетевого графика, его
проверка, устранение ошибок и упрощение.
4. Расчёт исходного сетевого графика.
5. Оптимизация (улучшение).
6. Построение масштабного сетевого графика.

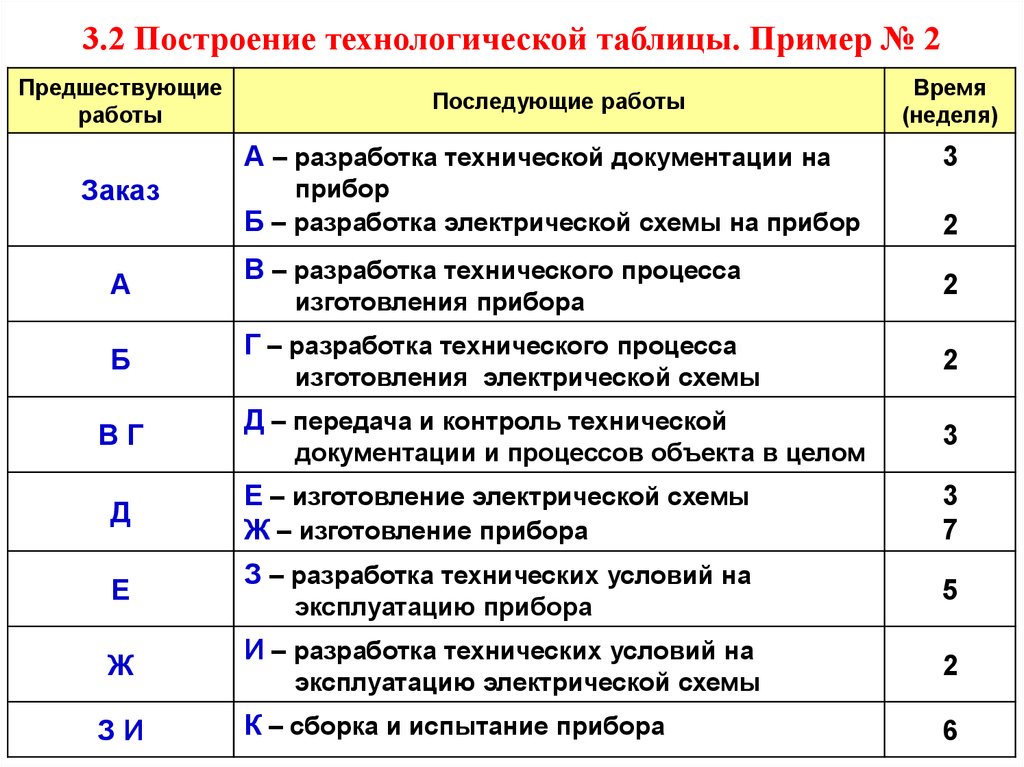
17. 3.2 Построение технологической таблицы. Пример № 2

Предшествующие
работы
Заказ
А
Б
ВГ
Д
Е
Ж
ЗИ
Последующие работы
Время
(неделя)
А – разработка технической документации на
3
прибор
Б – разработка электрической схемы на прибор
2
В – разработка технического процесса
изготовления прибора
Г – разработка технического процесса
изготовления электрической схемы
Д – передача и контроль технической
документации и процессов объекта в целом
Е – изготовление электрической схемы
Ж – изготовление прибора
З – разработка технических условий на
эксплуатацию прибора
И – разработка технических условий на
эксплуатацию электрической схемы
К – сборка и испытание прибора
2
2
3
3
7
5
2
6

18. 3.3 Определение продолжительности выполнения работы и других числовых характеристик

Числовые характеристики
числовыми способами:
могут
определяться
1. Использование научно обоснованных нормативов,
приказов, инструкций, наставлений, и т.д.
2. Выполнение соответствующих расчётов.
3. Статистическая
опыта.
обработка
4. Метод экспертных оценок.
результатов
прошлого

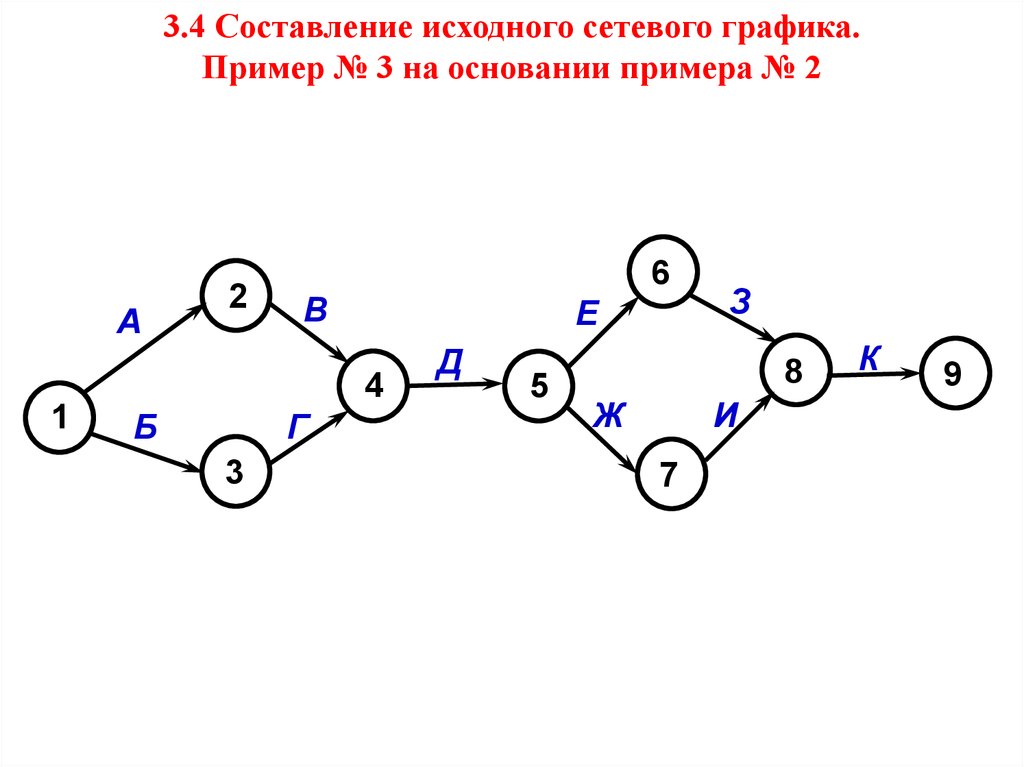
19. 3.4 Составление исходного сетевого графика. Пример № 3 на основании примера № 2

А
2
6
В
Е
4
1
Б
Г
3
Д
5
З
8
Ж
И
7
К
9

20. 3.5 Порядок расчёта сетевого графика (по критерию времени)

Расчёт сетевого графика
по времени
по расходу средств
Основные показатели:
t(i,j) – продолжительность любой работы i,j;
tp(i) – ранний срок совершения события;
Ткр – критическое время;
tn(i) – поздний срок совершения события;
Р(i) – резерв времени события i;
Р(i) = tn(i) - tp(i) [1]
Рn(i,j) – полный резерв времени работы i,j;
Рn(i,j) = tn(j) - tp(i) - t(i,j) [2]
Рс(i,j) – свободный резерв времени работы i,j;
Рс(i,j) = tр(j) - tp(i) - t(i,j) [3]
На практике используют табличный (с помощью ЭВМ) и 4х
секторный (ручной) способы.

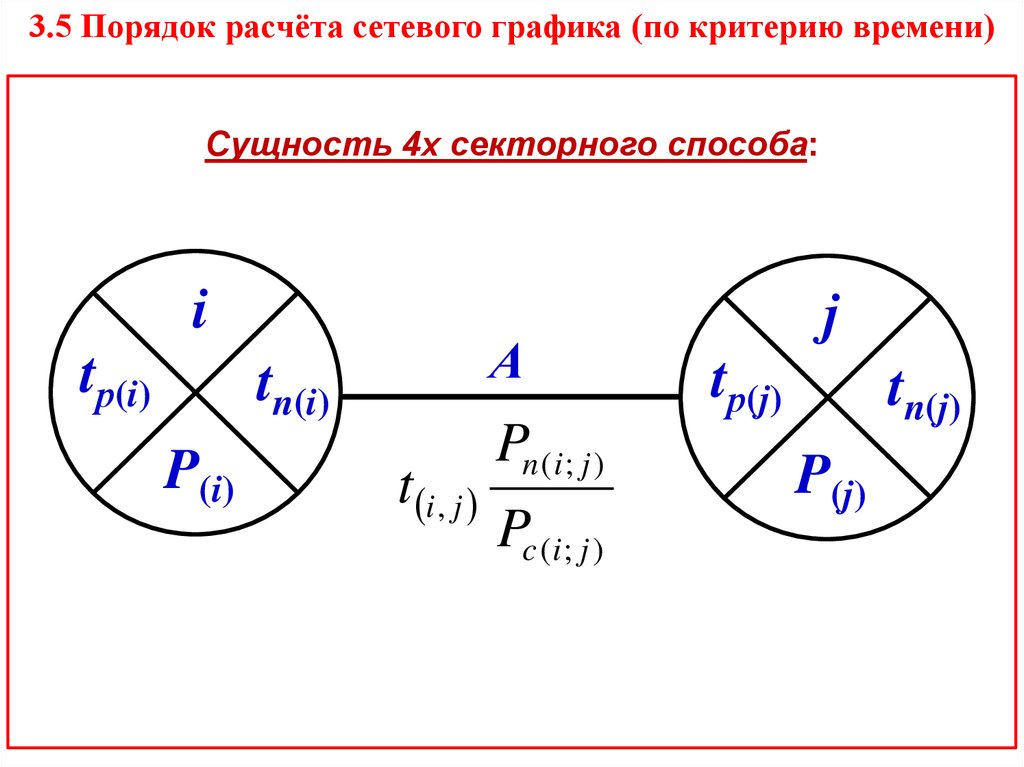
21. 3.5 Порядок расчёта сетевого графика (по критерию времени)

Сущность 4х секторного способа:
i
tр(i)
А
tn(i)
P(i)
t i , j
Pn ( i ; j )
Pc ( i ; j )
j
tр(j)
tn(j)
P(j)

22. 3.5 Порядок расчёта сетевого графика (по критерию времени)

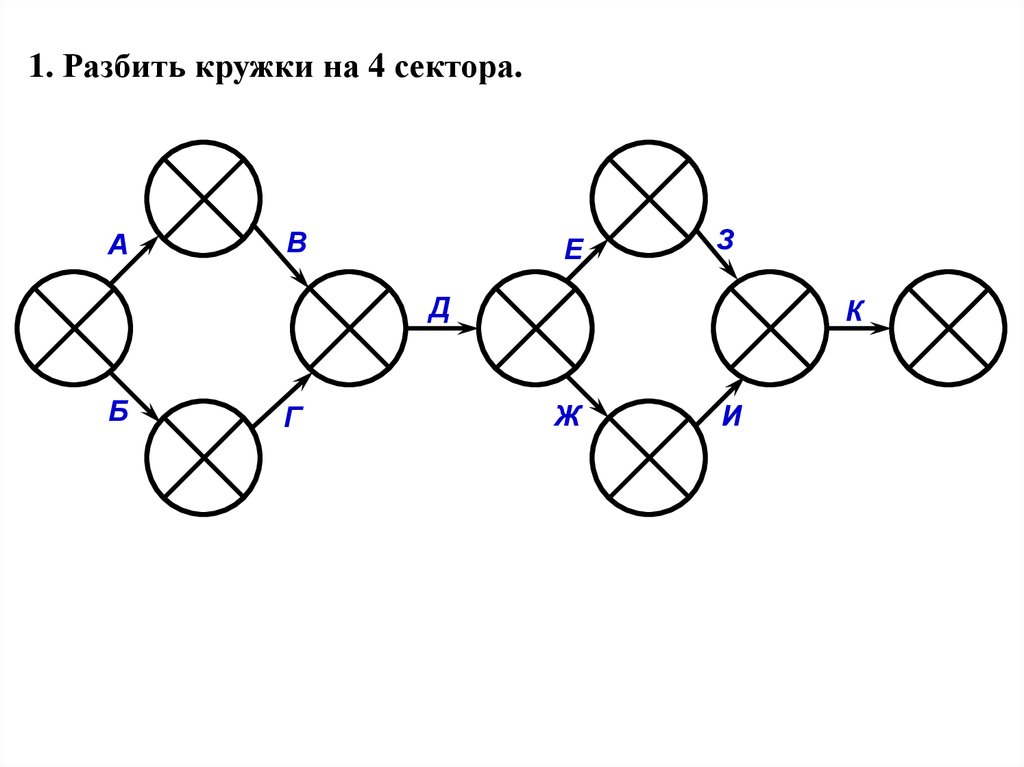
Алгоритм способа расчёта 4х секторным способом:
I. Подготовка сетевого графика к расчёту
1. Разбить кружки на 4 сектора.
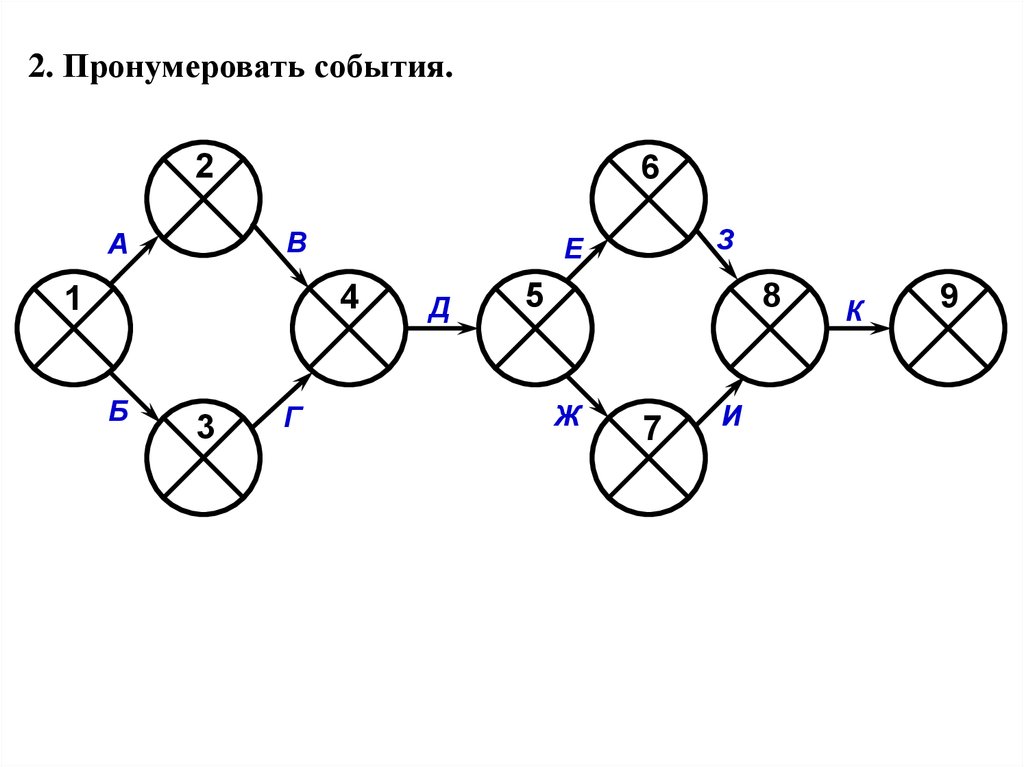
2. Пронумеровать события.
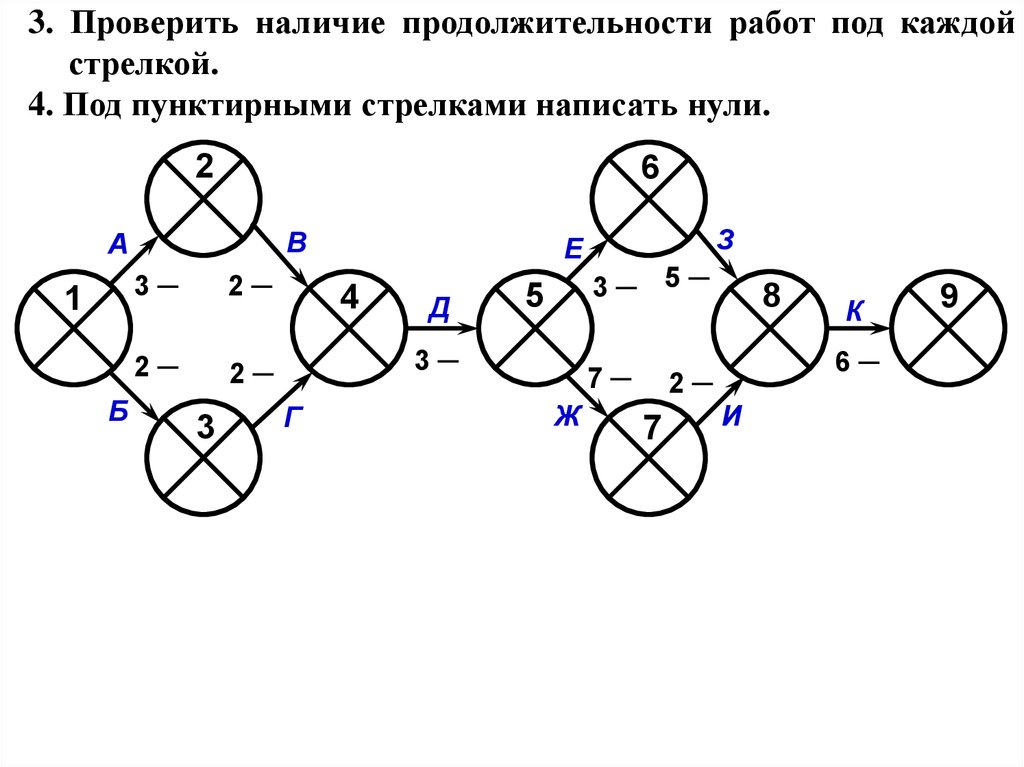
3. Проверить наличие продолжительности работ под каждой
стрелкой.
4. Под пунктирными стрелками написать нули.
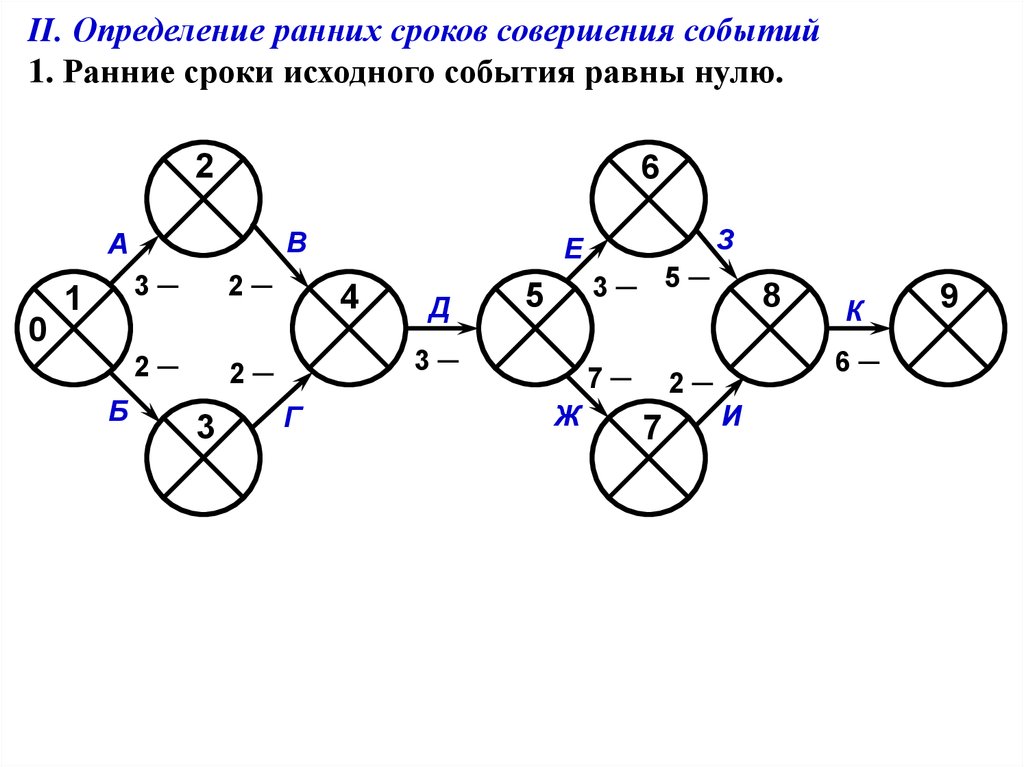
II. Определение ранних сроков совершения событий
1. Ранние сроки исходного события равны нулю.
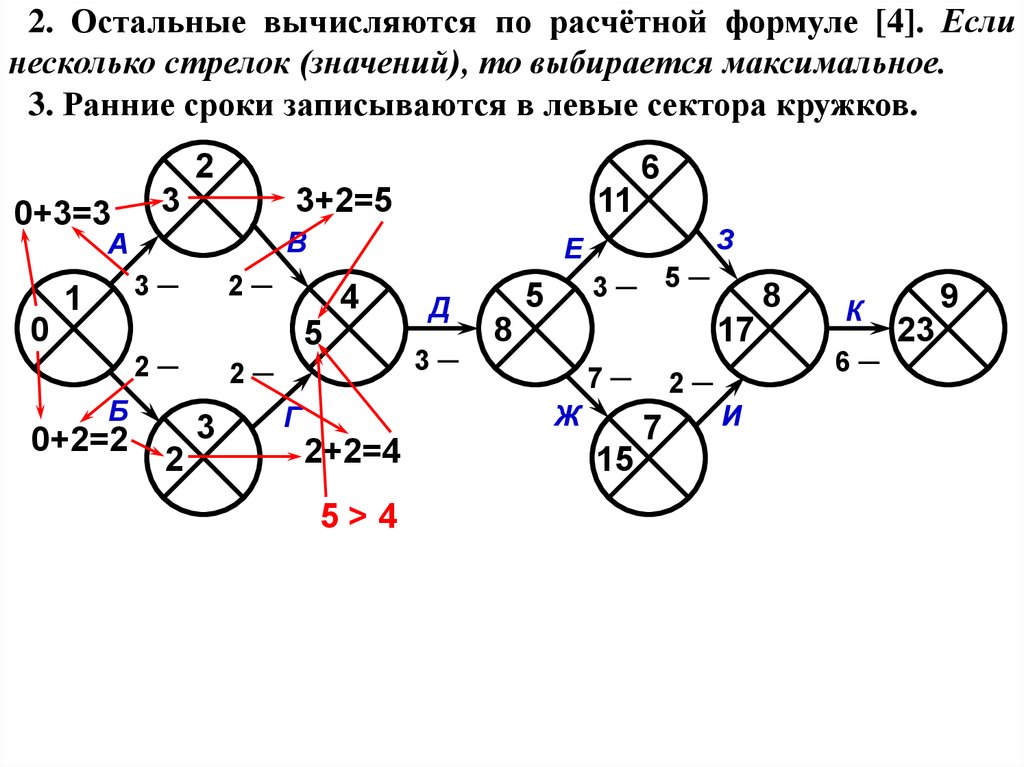
2. Остальные вычисляются по расчётной формуле
tp(j) = max [tp(i) + t(i,j)]
[4]
ij
Если несколько стрелок (значений), то выбирается
максимальное.
3. Ранние сроки записываются в левые сектора кружков.

23.

Алгоритм способа расчёта 4х секторным способом
(продолжение):
III.
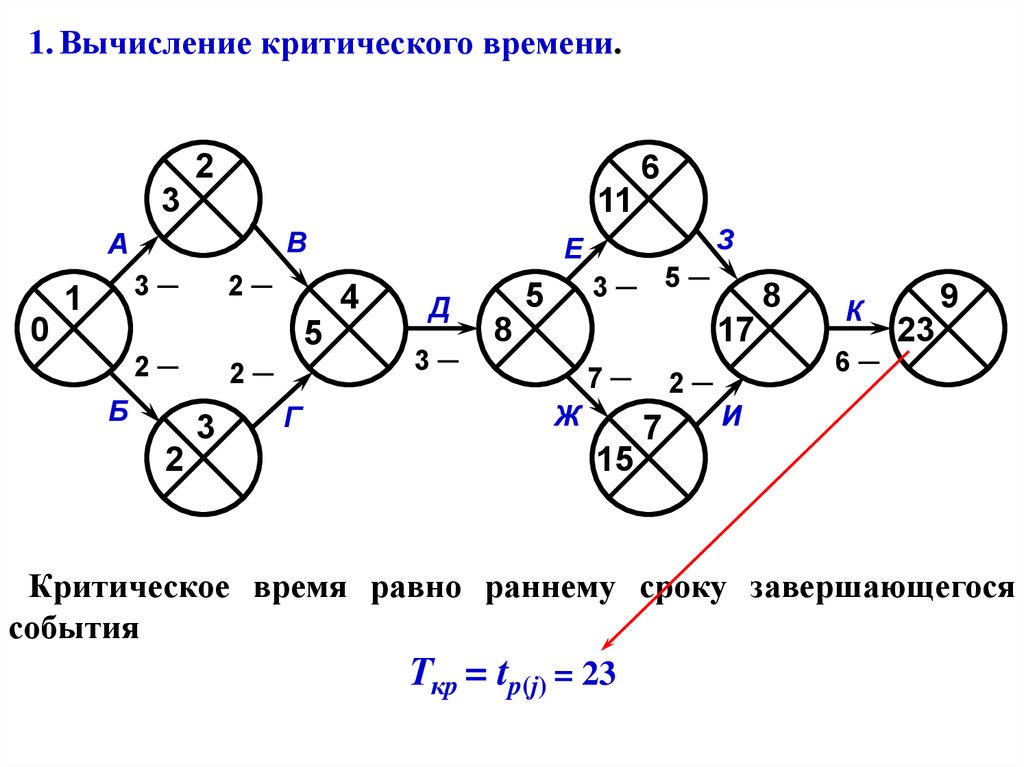
1. Вычисление критического времени, которое равно раннему
сроку завершающегося события
Ткp = tp(j)
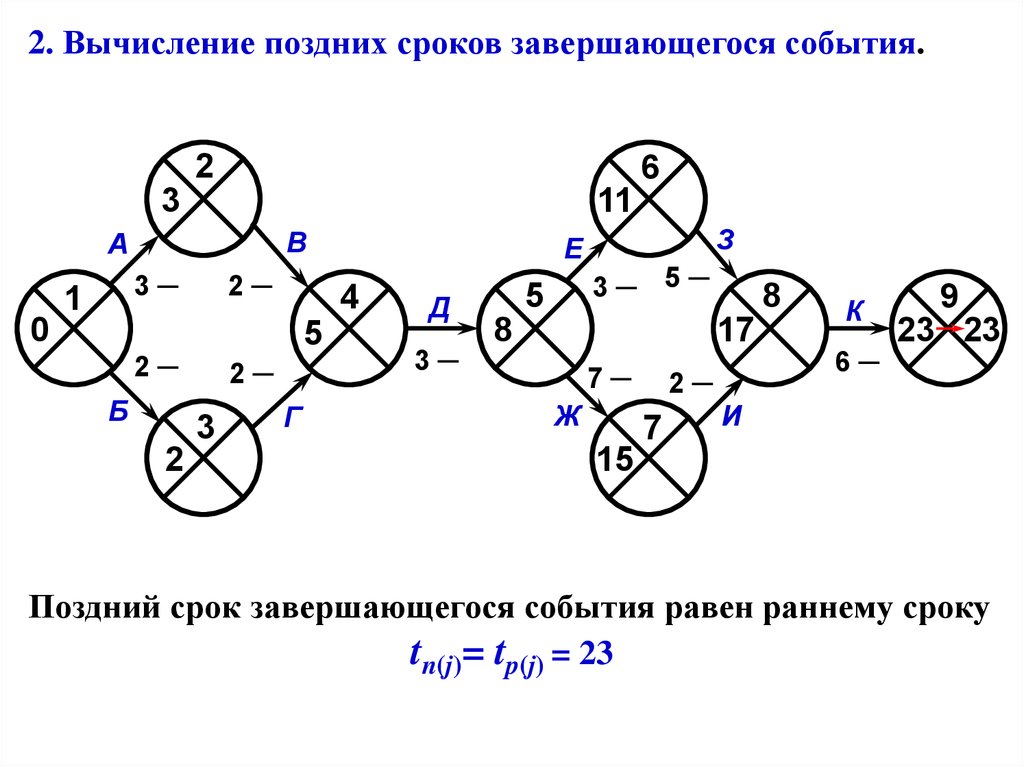
2. Вычисление поздних сроков завершающегося события.
Поздний срок завершающегося события равен раннему сроку
tn(j)= tp(j)
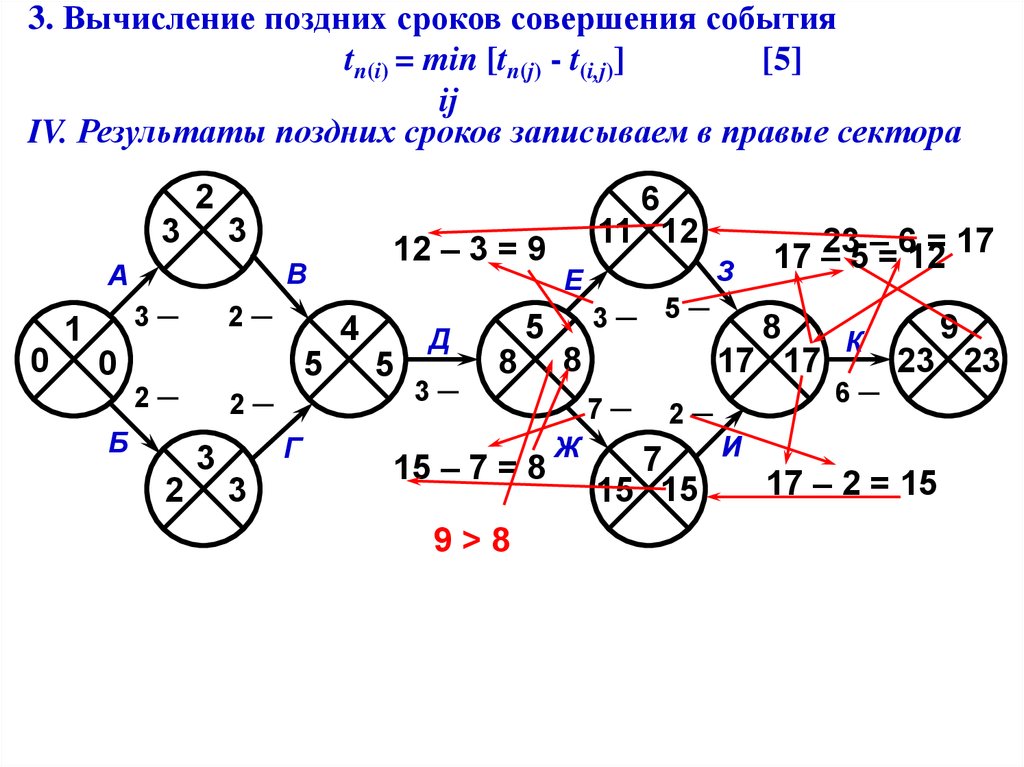
3. Вычисление поздних сроков совершения события
tn(i) = min [tn(j) - t(i,j)]
ij
[5]

24.

Алгоритм способа расчёта 4х секторным способом
(продолжение):
IV. Результаты поздних сроков записываем в правые сектора
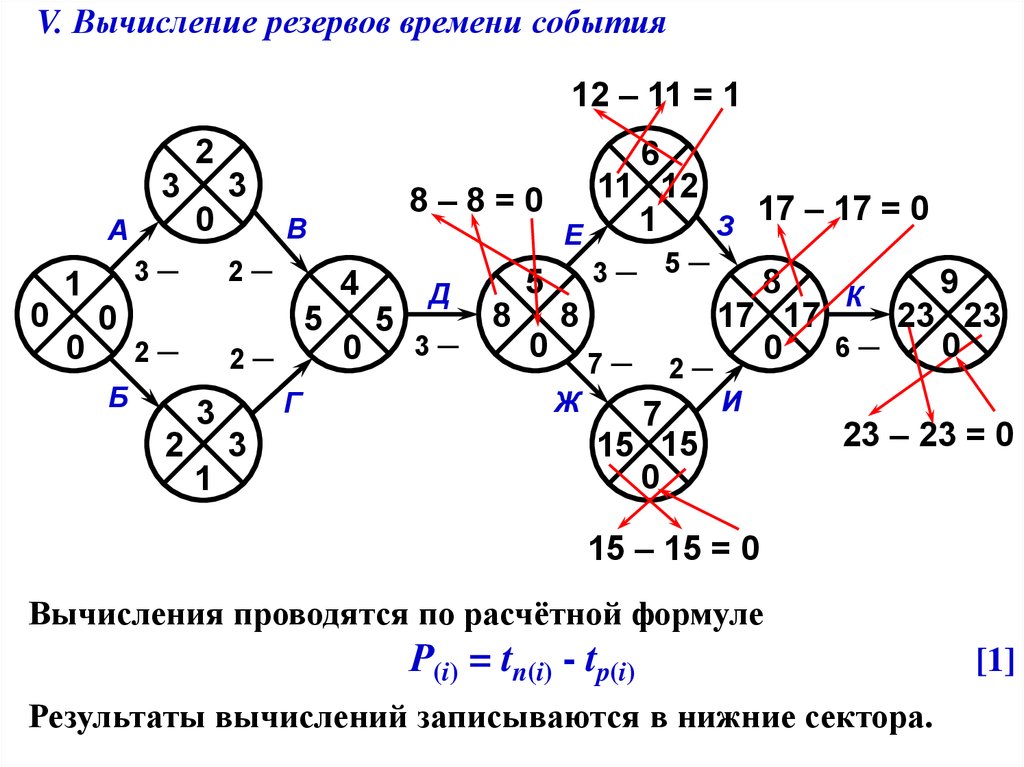
V. Вычисление резервов времени события
Вычисления проводятся по расчётной формуле № 1
Р(i) = tn(i) - tp(i)
Результаты вычислений записываются в нижние сектора.
[1]

25.

Алгоритм способа расчёта 4х секторным способом
(продолжение):
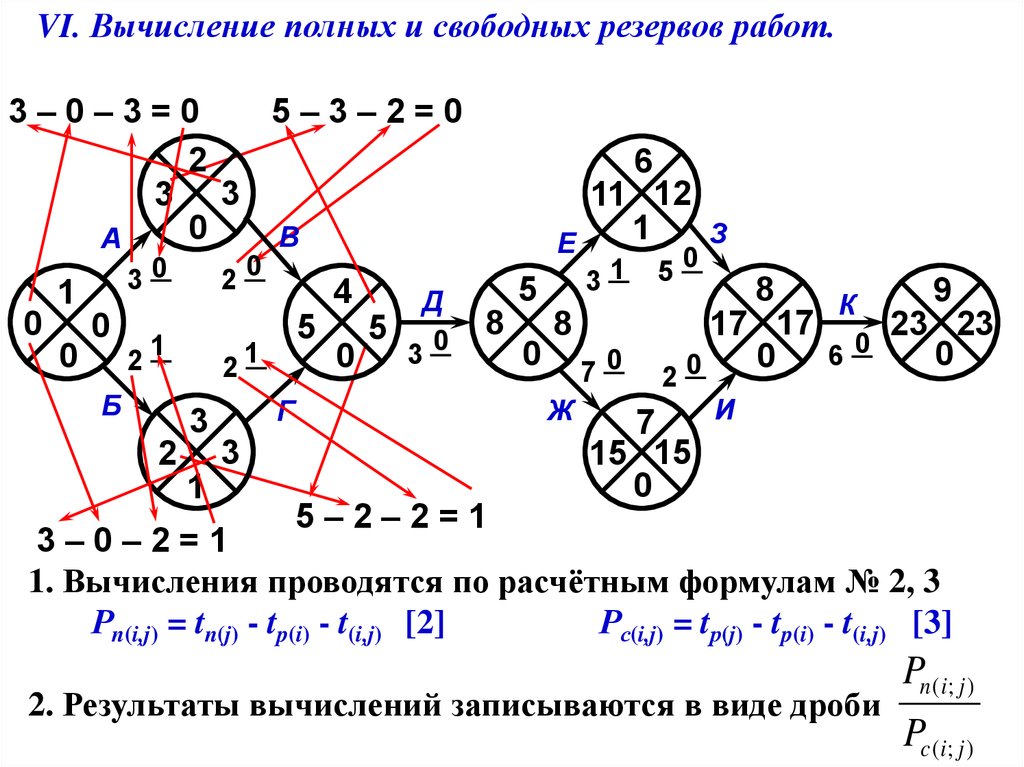
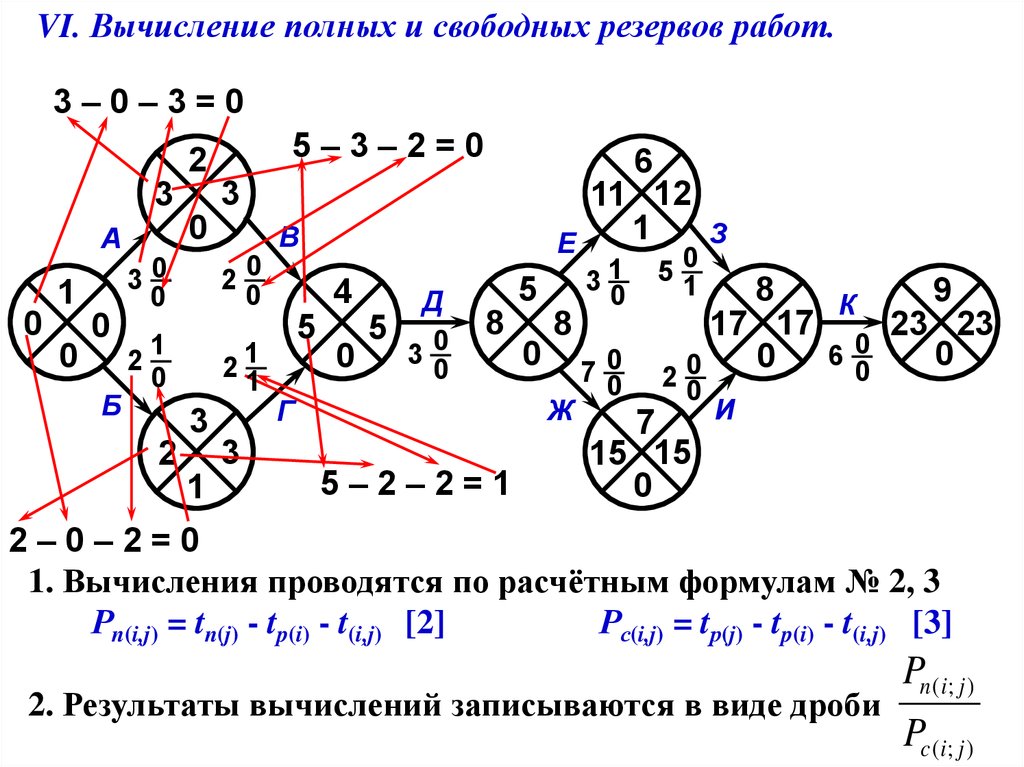
VI. Вычисление полных и свободных резервов работ.
1. Вычисления проводятся по расчётным формулам № 2, 3
Рn(i,j) = tn(j) - tp(i) - t(i,j)
[2]
Рс(i,j) = tр(j) - tp(i) - t(i,j)
[3]
2. Результаты вычислений записываются в виде дроби
Pn (i ; j )
Pc (i ; j )

26.

Алгоритм способа расчёта 4х секторным способом
(продолжение):
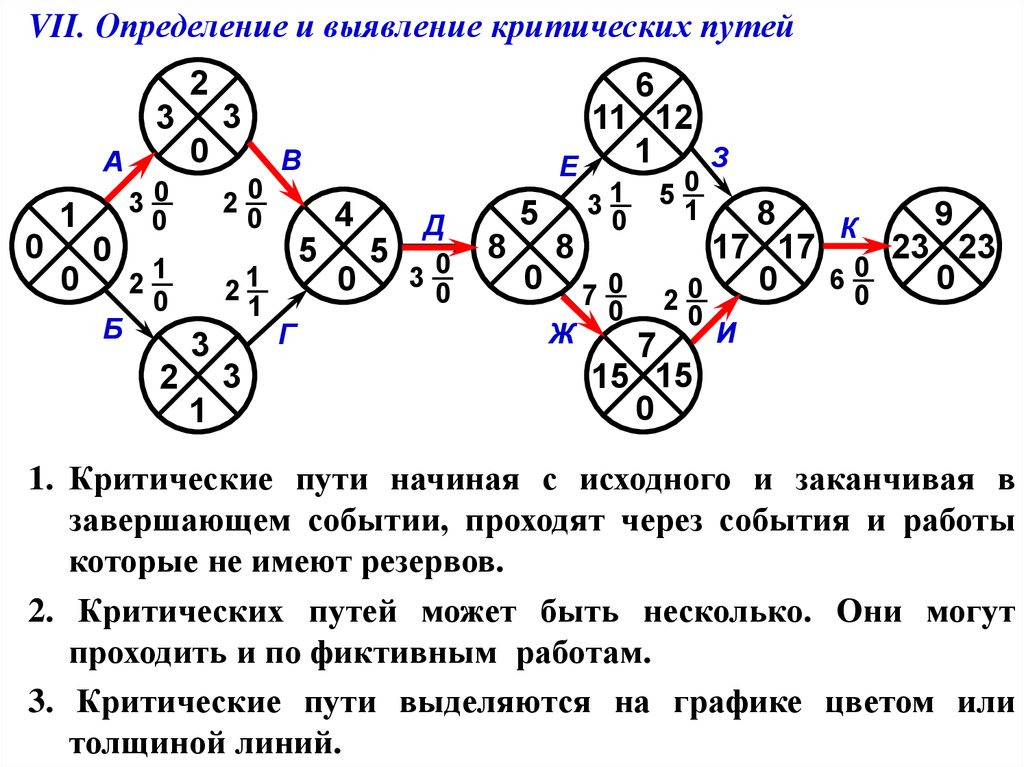
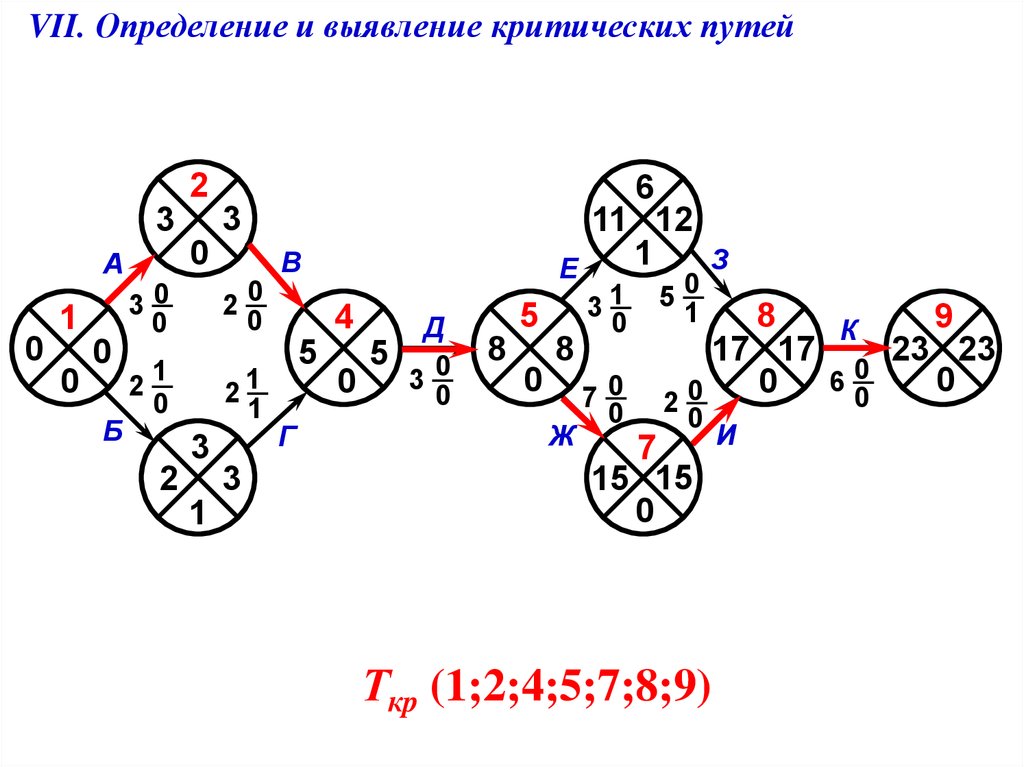
VII. Определение и выявление критических путей
1. Критические пути начиная с исходного и заканчивая в
завершающем событии, проходят через события и работы
которые не имеют резервов.
2. Критических путей может быть несколько. Они могут
проходить и по фиктивным работам.
3. Критические пути выделяются на графике цветом или
толщиной линий.

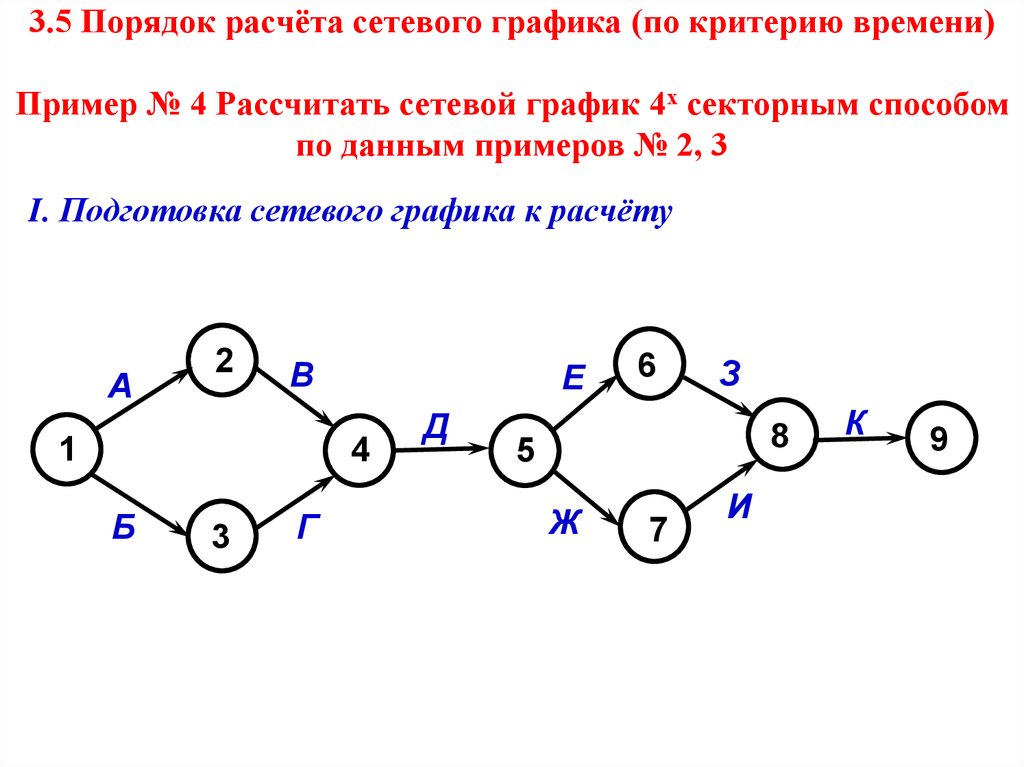
27. 3.5 Порядок расчёта сетевого графика (по критерию времени) Пример № 4 Рассчитать сетевой график 4х секторным способом по данным примеров № 2,

3.5 Порядок расчёта сетевого графика (по критерию времени)
Пример № 4 Рассчитать сетевой график 4х секторным способом
по данным примеров № 2, 3
I. Подготовка сетевого графика к расчёту
А
2
В
1
Е
4
Б
3
Г
Д
6
З
8
5
Ж
7
И
К
9

28.

1. Разбить кружки на 4 сектора.
А
В
Е
З
Д
Б
Г
К
Ж
И

29.

2. Пронумеровать события.
2
6
В
А
4
1
Б
3
Г
З
Е
Д
5
8
Ж
7
И
К
9

30.

3. Проверить наличие продолжительности работ под каждой
стрелкой.
4. Под пунктирными стрелками написать нули.
2
6
В
А
1
Б
3─
2─
2─
2─
3
4
Д
5─
3─
5
3─
Г
З
Е
7─
Ж
8
6─
2─
7
К
И
9

31.

II. Определение ранних сроков совершения событий
1. Ранние сроки исходного события равны нулю.
2
6
В
А
0
1
Б
3─
2─
2─
2─
3
4
Д
5─
3─
5
3─
Г
З
Е
7─
Ж
8
6─
2─
7
К
И
9

32.

2. Остальные вычисляются по расчётной формуле [4]. Если
несколько стрелок (значений), то выбирается максимальное.
3. Ранние сроки записываются в левые сектора кружков.
2
0+3=3
6
3
3+2=5
В
А
0
3─
1
Б
2
4
5
2─
3
З
Е
2─
2─
0+2=2
11
Д
3─
5
8
2+2=4
5>4
8
17
7─
Ж
Г
5─
3─
15
2─
7
И
К
6─
9
23

33.

1. Вычисление критического времени.
2
6
3
11
В
А
0
3─
1
2─
2─
Б
2─
3
2
4
5
Г
З
Е
Д
3─
5─
3─
5
8
8
17
7─
Ж
15
2─
7
К
6─
9
23
И
Критическое время равно раннему сроку завершающегося
события
Ткp = tp(j) = 23

34.

2. Вычисление поздних сроков завершающегося события.
2
6
3
11
В
А
0
3─
1
2─
2─
Б
2─
3
2
4
5
Г
З
Е
Д
3─
5─
3─
5
8
8
17
7─
Ж
15
2─
7
К
6─
9
23 23
И
Поздний срок завершающегося события равен раннему сроку
tn(j)= tp(j) = 23

35.

3. Вычисление поздних сроков совершения события
tn(i) = min [tn(j) - t(i,j)]
[5]
ij
IV. Результаты поздних сроков записываем в правые сектора
2
3
3
0
3─
0
12 – 3 = 9
В
А
1
6
2─
5
2─
Б
2─
3
2
4
Г
3
5
Д
3─
11 12
3─
5
8
15 – 7 = 8
9>8
З
Е
5─
8
8
17 17
7─
Ж
235–=612
= 17
17 –
2─
К
6─
9
23 23
И
7
17 – 2 = 15
15 15

36.

V. Вычисление резервов времени события
12 – 11 = 1
2
3
3
0
А
0
3─
1
0
0
4
5
2─
3
2
1
Г
3
11 12
17 – 17 = 0
1
З
Е
5─
5 3─
8
9
К
8 8
23 23
17 17
0 7─
0
6─
0
8–8=0
В
2─
2─
Б
6
0
5
Д
3─
2─
Ж
И
7
15 15
0
23 – 23 = 0
15 – 15 = 0
Вычисления проводятся по расчётной формуле
Р(i) = tn(i) - tp(i)
Результаты вычислений записываются в нижние сектора.
[1]

37.

VI. Вычисление полных и свободных резервов работ.
3–0–3=0
5–3–2=0
2
3 3
0
В
А
0
1
0
0
2─
0
3─
0
1
2─
Б
4
5
2 1─
3
2
1
Г
3
0
Д
5 0
3─
6
11 12
1
З
Е
0
5
1 5─
3─
8
9
К
8 8
23 23
17 17
0
6─
0 7─
0
0
0
0
2─
И
Ж
7
5–2–2=1
15 15
0
3–0–2=1
1. Вычисления проводятся по расчётным формулам № 2, 3
Рn(i,j) = tn(j) - tp(i) - t(i,j) [2]
Рс(i,j) = tр(j) - tp(i) - t(i,j) [3]
2. Результаты вычислений записываются в виде дроби
Pn (i ; j )
Pc (i ; j )

38.

VI. Вычисление полных и свободных резервов работ.
3–0–3=0
5–3–2=0
2
3
3
0
А
0
1
0
0
Б
6
В
0
3─
0
0
2─
0
1
2─
0
21
─
1
3
2
1
11 12
1
З
Е
0
3
4
Д
5
5 0
3─
0
0
Г
5
5─
31
─
1
0
8
9
К
8 8
23 23
17 17
0
6─
0 7─
0
0
0
0
0
0 2─
0
И
Ж
7
5–2–2=1
15 15
0
2–0–2=0
1. Вычисления проводятся по расчётным формулам № 2, 3
Рn(i,j) = tn(j) - tp(i) - t(i,j) [2]
Рс(i,j) = tр(j) - tp(i) - t(i,j) [3]
2. Результаты вычислений записываются в виде дроби
Pn (i ; j )
Pc (i ; j )

39.

VII. Определение и выявление критических путей
2
3
3
0
А
0
1
0
0
Б
6
В
0
3─
0
0
2─
0
1
2─
0
2 1─
1
3
2
1
11 12
1
З
Е
0
3
4
Д
5
5 0
3─
0
0
Г
5
31
─
0
5─
1
8
9
К
8 8
23 23
17 17
0
6─
0 7─
0
0
0
0
0
0 2─
0
И
Ж
7
15 15
0
1. Критические пути начиная с исходного и заканчивая в
завершающем событии, проходят через события и работы
которые не имеют резервов.
2. Критических путей может быть несколько. Они могут
проходить и по фиктивным работам.
3. Критические пути выделяются на графике цветом или
толщиной линий.

40.

VII. Определение и выявление критических путей
2
3
3
0
А
0
1
0
0
Б
6
В
0
3─
0
0
2─
0
1
2─
0
2 1─
1
3
2
1
11 12
1
З
Е
0
3
4
Д
5
5 0
3─
0
0
Г
5
31
─
0
5─
1
8
9
К
8 8
23 23
17 17
0
6─
0 7─
0
0
0
0
0
0 2─
0
И
Ж
7
15 15
0
Ткp (1;2;4;5;7;8;9)

41.

Задачи выбора маршрута
Типичной
задачей
выбора
маршрута
является
нахождение некоторого маршрута проезда из одного
города в другой, при наличии множества путей через
различные промежуточные пункты. Задача состоит в
определении наиболее экономичного маршрута по
критерию
времени,
расстояния
или
стоимости
проезда. На существующие маршруты могут быть
наложены ограничения, например, запрет на возврат к
уже
пройденному
пути,
требование
обхода
всех
пунктов, причем в каждом из них модно побывать
только один раз (задача коммивояжера).