Solução Numérica de Equações Diferenciais

1.

UNIVERSIDADE FEDERAL DE UBERLÂNDIA
FACULDADE DE MATEMÁTICA
PROJETO PIBEG
Unidade VI
Solução Numérica de
Equações Diferenciais
1
Ordinárias
0011 0010
452

2.

INTRODUÇÃO
Uma equação diferencial ordinária é definida como uma equação
que envolve uma função incógnita y e algumas de suas derivadas
avaliadas em uma variável independente x, da forma:
y( n ) ( x ) f [ x , y' ( x ), y' ' ( x ),... , y( n 1 ) ( x )]
Nas ciências aplicadas a utilização de equações diferenciais tem
como objetivo descrever o comportamento dinâmico de sistemas
físicos. Por exemplo, o comportamento dinâmico de um circuito,
1
452
mostrado na figura a seguir, pode ser descrito por uma equação
diferencial.
0011 0010

3.

CIRCUITOS ELÉTRICOS RLC
Circuitos elétricos mais complexos são basicamente formados
por resistores de resistência R, indutores de indutância L,
capacitores de capacitância C, carregado com uma diferença
de potencial VC e uma fonte elétrica cuja diferença de potencial
é indicada E(t).
0011 0010
1
452

4.

Se E(t) é a diferença de potencial da fonte de alimentação e i(t) é
a intensidade da corrente elétrica, então:
VL é a diferença de potencial nos terminais do indutor:
di
VL (t ) L
dt
VR é a diferença de potencial nos terminais do resistor:
VR (t ) Ri (t )
0011 0010
1
452

5.

VC é a diferença de potencial nos terminais do capacitor:
1 t
VC (t ) i (u )du
C 0
A lei de Kirchoff para tensões afirma que a soma algébrica de
todas as tensões tomadas num sentido determinado (horário ou
anti-horário), em torno de um circuito fechado é nula. Assim,
quando for fechado o interruptor, obteremos:
VL (t ) VR (t ) VC (t ) E (t )
0011 0010
1
452

6.

Substituindo
di
VL (t ) L
dt
em
VR (t ) Ri (t )
1 t
VC (t ) i (u )du
C 0
VL (t ) VR (t ) VC (t ) E (t )
obtemos:
di
1 t
L Ri (t ) i (u )du E (t )
dt
C 0
0011 0010
1
452

7.

Se E(t) é constante e derivarmos em relação à variável t, teremos
d 2i(t )
di(t ) 1
L
R
i(t ) 0
2
dt
dt
C
e temos uma EDO de segunda ordem, linear e homogênea.
Se E(t) é uma função diferenciável da variável t, então
d 2i(t )
di(t ) 1
dE
L
R
i(t )
2
dt
dt
C
dt
e temos uma EDO linear não-homogênea.
0011 0010
1
452

8.

TIPOS DE EQUAÇÕES
DIFERENCIAIS
0011 0010
1
452

9.

EQUAÇÕES DIFERENCIAIS ORDINÁRIAS
São equações diferenciais que possuem apenas uma
variável independente.
Exemplos:
dy
x y
dx
y é função de x e x é a única variável
independente.
dy
x2 y2
dt
y e x são funções de t; t é a única
d2y
2
2
x
y
dw2
y e x são funções de w; w é a
0011 0010
variável independente.
única variável independente. Esta
edo é de segunda ordem.
1
452

10.

EQUAÇÕES DIFERENCIAIS PARCIAIS
Uma equação diferencial parcial é aquela cuja função
incógnita depende de duas ou mais variáveis independentes.
Exemplo:
2u 2u
2 0
2
x y
0011 0010
u é função de x e y; x e y são variáveis
independentes. EDP linear, de 2ª
ordem e homogênea. (Equação de
Laplace)
1
452

11.

SOLUÇÃO DE EQUAÇÕES DIFERENCIAIS
Determinadas
equações
diferenciais
podem
ser
solucionadas analiticamente, cuja solução é uma expressão
literal. No entanto, isto nem sempre é possível. Neste caso,
a
solução é obtida através de solução numérica, como será visto
na seqüência.
0011 0010
1
452

12.

Exemplo:
dy
y.
Resolva a equação diferencial
dx
Solução:
dy
dy
dy
y
dx
dx ln( y) c1 x c2
dx
y
y
y ( x) e x c e x e c .
Tomando k ec obtemos :
y( x) ke
x
0011 0010
1
452

13.

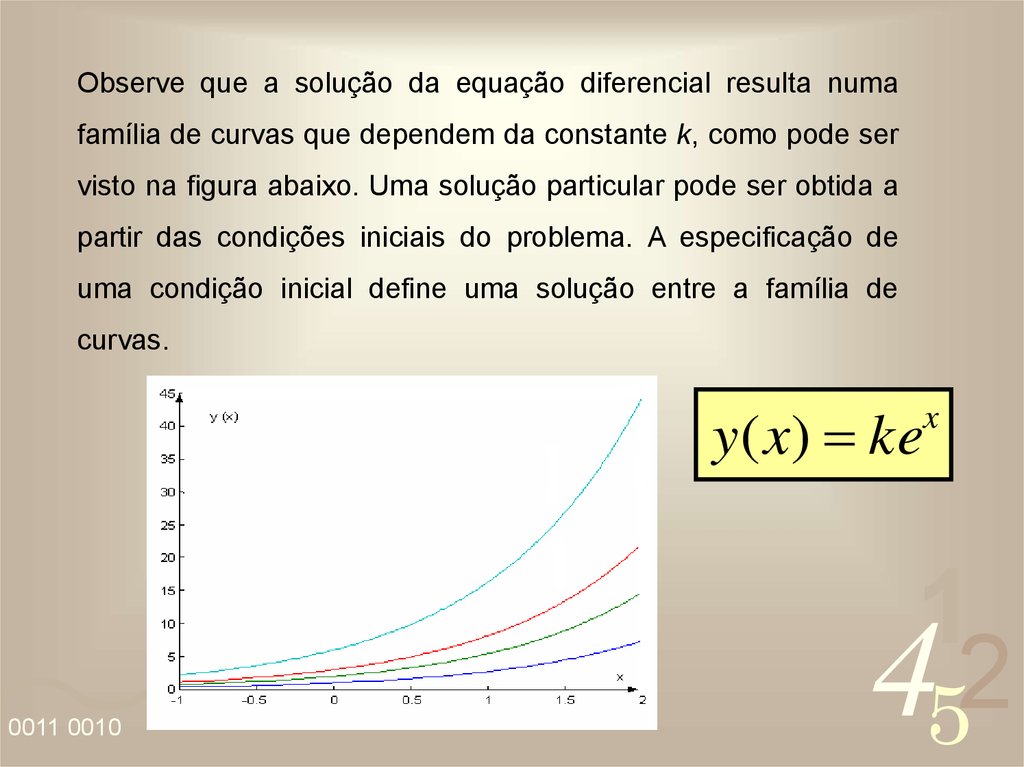
Observe que a solução da equação diferencial resulta numa
família de curvas que dependem da constante k, como pode ser
visto na figura abaixo. Uma solução particular pode ser obtida a
partir das condições iniciais do problema. A especificação de
uma condição inicial define uma solução entre a família de
curvas.
y( x) ke
x
0011 0010
1
452

14.

SOLUÇÃO NUMÉRICA DE
EQUAÇÕES DIFERENCIAIS
ORDINÁRIAS – PROBLEMA DE
VALOR INICIAL
0011 0010
1
452

15.

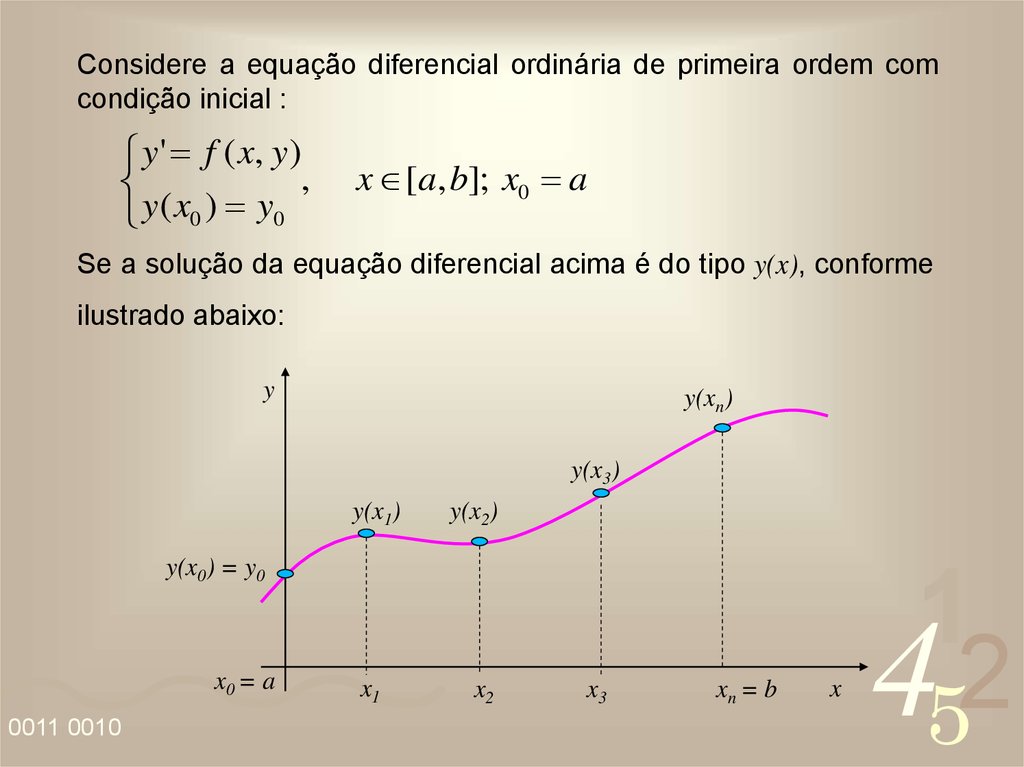
Considere a equação diferencial ordinária de primeira ordem com
condição inicial :
y' f ( x, y)
,
y( x0 ) y0
x [a, b]; x0 a
Se a solução da equação diferencial acima é do tipo y(x), conforme
ilustrado abaixo:
y
y(xn)
y(x3)
y(x1)
y(x2)
y(x0) = y0
x0 = a
0011 0010
x1
x2
x3
xn = b
x
1
452

16.

então a solução numérica da equação diferencial é obtida
aproximando-se os valores y( x0 ), y( x1 ), y( x2 ), y( x3 ),... , y( xn ) ,
conforme a tabela abaixo:
b a
onde xj = x0 + jh, com h
e n é o número de subintervalos
n
de [a,b].
Considera-se que a notação y ( x j ), j 1,2,..., n indica a solução
exata da EDO nos pontos x1 , x 2 , x3 ,..., x n, e y j , j 1,2,...., n
1
452
indica a solução aproximada obtida por um método numérico.
0011 0010

17.

Na solução numérica não se determina a expressão literal da
função y(x), mas sim uma solução aproximada do PVI num
conjunto discreto de pontos.
Nos problemas das ciências aplicadas, normalmente estuda-se
o comportamento dinâmico de determinadas variáveis, portanto
necessita-se da evolução das variáveis em função da variável
independente. A partir dos dados numéricos é possível gerar um
esboço do gráfico da função incógnita.
0011 0010
1
452

18.

MÉTODOS BASEADOS
NA SÉRIE DE TAYLOR
1
452
Série de Taylor
Resumo
0011 0010

19.

Suponhamos
que,
de
alguma
forma,
tenhamos
as
aproximações y1, y2, ..., yi para y(x), em x1, x2, ..., xi.
Se y for suficientemente “suave”, a série de Taylor de y(x) em torno
de x = xi é:
( x xi ) 2
( x xi ) k
( x xi ) k 1
(k )
( k 1)
y( x) y( xi ) y' ( xi )( x xi ) y" ( xi )
y ( xi )
y
( x )
2!
k!
(k 1)!
x entre xi e x.
Assim,
1
452
( xi 1 xi ) 2
( xi 1 xi ) k
(k )
y ( xi 1 ) y( xi ) y' ( xi )( xi 1 xi ) y" ( xi )
y ( xi )
2!
k!
0011 0010

20.

Se yi(j) representa a aproximação para a j-ésima derivada da função
y(x) em xi: y(j)(xi) e h = xi+1 – xi, teremos:
k
h2
h
(k )
y ( xi 1 ) yi 1 yi yi ' h yi " yi
2!
k!
e o erro de truncamento é dado por:
e( xi )
0011 0010
y ( k 1) ( xi )
(k 1)!
h ( k 1)
1
452

21.

Observamos que, se y(x) tem derivadas de ordem (k+1), contínua
num intervalo fechado I que contém os pontos sobre os quais
estamos fazendo a discretização, então existe:
M k 1 max | y ( k 1) ( x) |
x I
Assim, teremos um majorante para o erro de truncamento pois
| y ( k 1) ( x ) | M k 1
x I
k 1
1
452
M k 1h
| e( xi ) | max | e( x) |
Chk 1
x I
(k 1)!
0011 0010

22.

Um método numérico é dito de ordem p se existe uma constante C
tal que:
| e( xi 1 ) | Ch p 1
Onde C depende das derivadas da função que define a equação
diferencial.
Para aplicar o método da série de Taylor de ordem k:
(k )
y ''
y
yi 1 yi yi ' h i h 2 i h k
2!
k!
temos de calcular yi’, yi”, yi’’’, ..., yi(k).
0011 0010
1
452

23.

Agora, y’(x) = f(x, y(x)). Então:
y" f x ( x, y( x)) f y ( x, y( x)) y' ( x) f x f y f
Assim, por exemplo, o método de série de Taylor de 2ª ordem é:
h2
yi 1 yi hf ( xi , yi ) [ f x ( xi , yi ) f y ( xi , yi ) f ( xi , yi )], i 0,1,...
2
0011 0010
1
452

24.

Observe que
y ' ' ' ( x) f xx ( x, y ( x)) f xy ( x, y ( x)) y ' ( x)
[ f yx ( x, y ( x)) f yy ( x, y ( x)) y ' ( x)] y ' ( x) f y ( x, y ( x)) y"( x)
f xx f xy f ( f yx f yy f ) f f y ( f x f y f ),
A expressão da terceira derivada já nos mostra a dificuldade dos
cálculos de um método de Taylor de terceira ordem. Observe
ainda que todos esses cálculos são efetuados para cada i,
i = 1, ..., n.
0011 0010
1
452

25.

Os métodos que usam o desenvolvimento em série de Taylor
de y(x) teoricamente fornecem solução para qualquer equação
diferencial. No entanto, do ponto de vista computacional, os
métodos de série de Taylor de ordem mais elevada são
considerados inaceitáveis pois, a menos de uma classe restrita
de funções f(x,y) ( f(x,y) = x2 + y2, por exemplo), o cálculo das
derivadas totais envolvidas é extremamente complicado.
0011 0010
1
452

26.

MÉTODO DE PASSO UM
MÉTODO DE EULER
0011 0010
1
452

27.

Consideremos, o método de série de Taylor de ordem k = 1, ou
seja,
yi 1 yi hyi' yi hf ( xi , yi )
onde
e( xi 1 )
y" ( xi 1 )
2
h2
1
452
Este é o método de Euler, que é um método de série de Taylor de
ordem 1.
0011 0010

28.

INTERPRETAÇÃO GEOMÉTRICA DO MÉDODO DE EULER:
Como conhecemos x0 e y0 = f(x0), então sabemos calcular
y’(x0) =
f(x0,y0). Assim, a reta r0(x) que passa por (x0,y0), com coeficiente
angular y’(x0), é:
r0 ( x) y( x0 ) ( x x0 ) y' ( x0 )
Escolhido
h xk 1 xk
y( x1 ) y1 r0 ( x1 ) y( x0 ) hy' ( x0 )
ou seja
0011 0010
y1 y0 hf ( x0 , y0 ).
1
452

29.

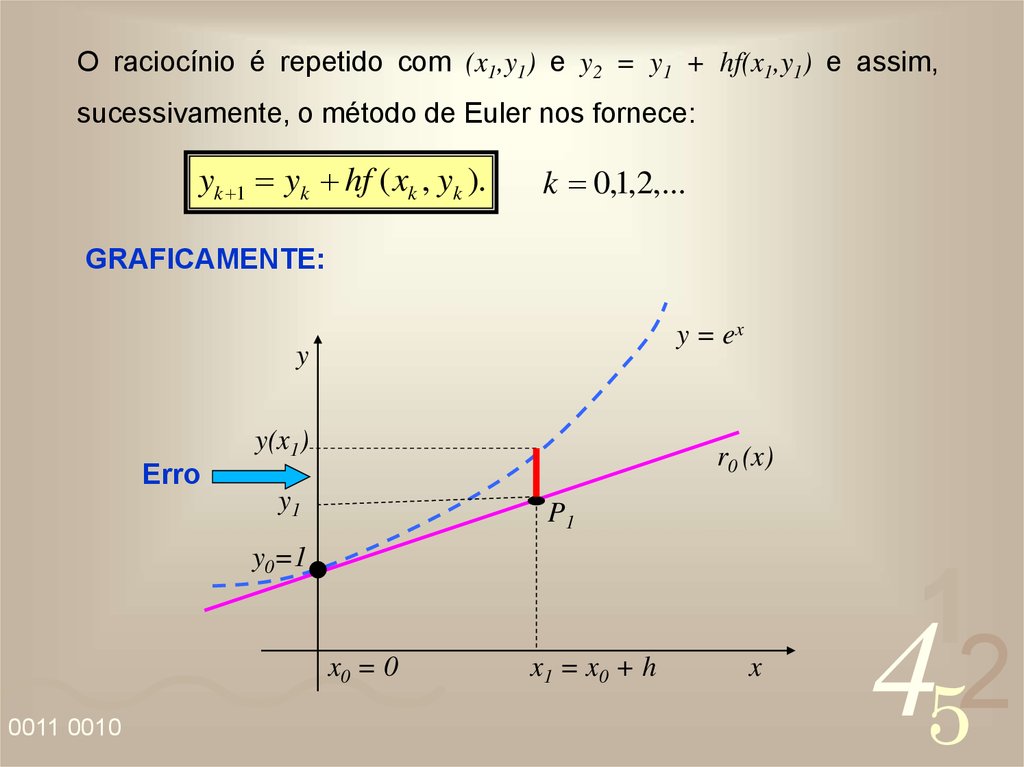
O raciocínio é repetido com (x1,y1) e y2 = y1 + hf(x1,y1) e assim,
sucessivamente, o método de Euler nos fornece:
yk 1 yk hf ( xk , yk ).
k 0,1,2,...
GRAFICAMENTE:
y = ex
y
y(x1)
Erro
r0 (x)
y1
P1
y0=1
x0 = 0
0011 0010
x1 = x0 + h
x
1
452

30.

EXEMPLO:
Seja o PVI: y’ = y, y(0) = 1. Trabalhando com quatro casas decimais,
usaremos o método de Euler para aproximar y(0.04)
com erro
menor do que ou igual a ; = 5×10-4.
O primeiro passo é encontrar h de modo que:
e( xi )
y" ( xi )
2
h2
Neste caso, conhecemos a solução analítica do PVI: y(x) = ex,
temos então que:
1
452
M 2 max | y" ( x) | e0.04 1.0408 | y" ( xi ) | M 2
x [ 0, 0.04]
0011 0010

31.

donde
1.0408 2
| e( x ) |
h
2
x I [0, 0.04]
1.0408 2
2 5 10 4
10 3
4
2
h 5 10 ; então h
2
1.0408
1.0408
Portanto,
h 0.0310.
Considerando pontos igualmente espaçados, tem-se h = 0.04/n,
onde n é o número de subintervalos de I. Assim,
0.04
0.04
0.0310 n
n 1.29 n 2.
n
0.031
Portanto, tomando n = 2, h = 0.02.
0011 0010
1
452

32.

Assim,
x0 0 e y ( x0 ) y (0) y0 1.
h
x1 0.02
x0
x2 0.04
Agora:
x2
x1
y ( x1 ) y1 y0 hf ( x0 , y0 ) y0 hy0
y0 (1 h) 1(1 0.02)
1.02
e
y ( x2 ) y2 y1 hf ( x1 , y1 ) y1 (1 h)
1.02(1.02) 1.02 2
1.0404
1
452
Dado que e0.04, com quatro casas decimais, vale 1.0408, temos que
o erro cometido foi 1.0408 – 1.0404 = 4×10-4 < 5×10-4.
0011 0010

33.

MÉTODOS DE
RUNGE-KUTTA
0011 0010
1
452

34.

MÉTODOS DE RUNGE-KUTTA
A idéia básica destes métodos é aproveitar as qualidades
dos métodos de série de Taylor (ordem elevada) e ao mesmo
tempo eliminar sua maior dificuldade que é o cálculo de
derivadas de f(x,y) que, conforme vimos, torna os métodos de
série de Taylor computacionalmente inaceitáveis.
0011 0010
1
452

35.

Podemos dizer que os métodos de Runge-Kutta de ordem p se
caracterizam pelas propriedades:
São de passo um (auto-iniciantes);
não exigem o cálculo de derivadas parciais de f(x,y);
necessitam apenas do cálculo de f(x,y) em determinados pontos
(os quais dependem da ordem dos métodos);
expandindo-se f(x,y) por Taylor em torno de (xi , yi) e agrupandose os termos em relação às potências de h, a expressão do método
1
452
de Runge-Kutta coincide com a do método de Taylor de mesma
ordem.
0011 0010

36.

MÉTODOS DE RUNGE-KUTTA DE 1ª ORDEM:
MÉTODO DE EULER
Já vimos que o método de Euler é um método de série de
Taylor de 1ª ordem:
yi 1 yi hf ( xi , yi ), i 0,1, 2, ...
Observe que o método de Euler possui as propriedades
anteriores que o caracterizam como um método de RungeKutta de ordem p = 1.
0011 0010
1
452

37.

MÉTODOS DE RUNGE-KUTTA DE 2ª ORDEM:
Inicialmente será apresentado um método particular que é o
método de Heun, ou método de Euler Aperfeiçoado, pois ele tem
uma interpretação geométrica bastante simples.
Conforme o próprio nome indica, este método consiste em fazer
mudanças no método de Euler para assim conseguir um método de
ordem mais elevada.
0011 0010
1
452

38.

MÉTODOS DE EULER APERFEIÇOADO:
INTERPRETAÇÃO GEOMÉTRICA
0011 0010
1
452

39.

Dado o PVI:
y' f ( x, y)
,
y( x0 ) y0
x [a, b]; x0 a
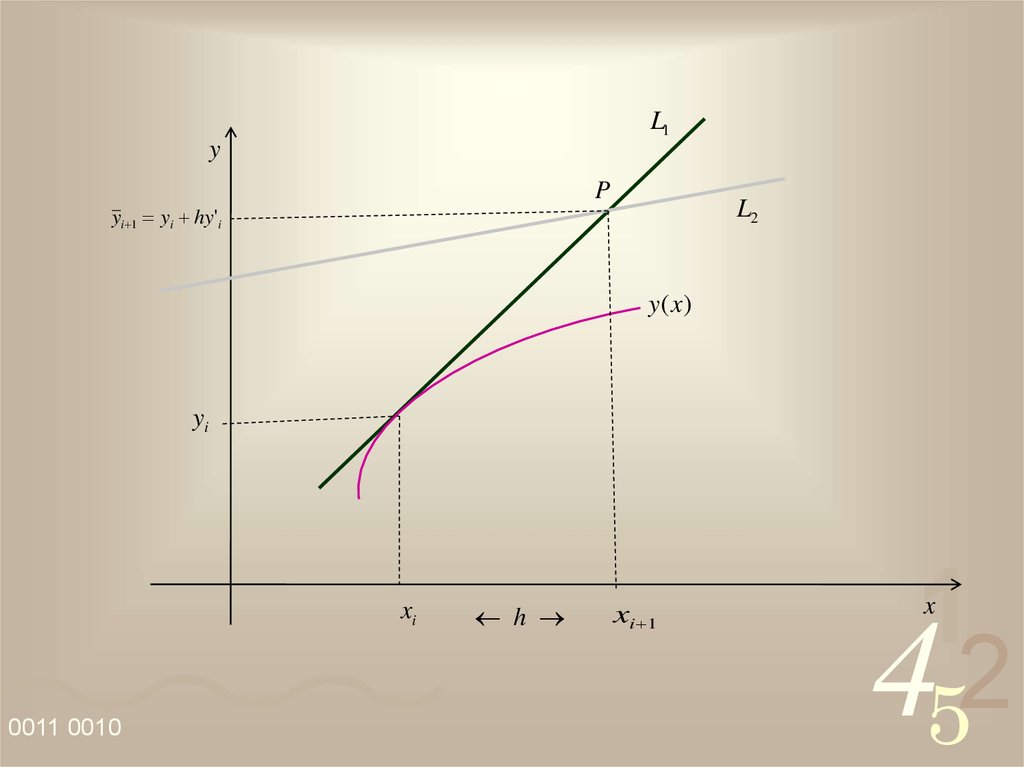
Considere o ponto (xi, yi), yi y(xi). Vamos supor a situação
ideal em que a curva desenhada com linha cheia seja a solução
y(x) da nossa equação ( isto só acontece mesmo em (x0, y0)).
Por (xi, yi) traçamos a reta L1 cujo coeficiente angular é
y’i = f(xi, yi), ou seja,
L1 : z1 (x) yi (x xi )yi ' yi (x xi )f(xi , yi ).
0011 0010
1
452

40.

L1
y
y (x) (Solução analítica)
yi
xi
0011 0010
1
452
x

41.

Assim, dado o passo h, z1(xi+1) = z1(xi + h) é igual ao valor yi+1
obtido do método de Euler, que chamamos aqui de
yi 1.
Seja
P (xi h, yi hy' i ) (xi 1 , yi 1 ).
Por P agora, traçamos a reta L2, com coeficiente angular
dado por:
f(xi h, yi hy' i ) f(xi 1 , yi 1 ).
L2 : z 2 (x) yi hy' i [x (xi h)]f(xi h, yi hy' i )
0011 0010
1
452

42.

L1
y
P
yi 1 yi hy'i
L2
y (x)
yi
xi
0011 0010
h
xi 1
1
452
x

43.

A reta pontilhada L0 passa por P e tem inclinação dada pela
média aritmética das inclinações das retas L1 e L2, ou seja, sua
inclinação é:
f(xi , yi ) f(xi h, yi hy'i )
2
0011 0010
1
452

44.

L1
L0
y
P
yi 1 yi hy'i
L2
y (x)
yi
xi
0011 0010
h
xi 1
1
452
x

45.

A reta pontilhada L0 passa por P e tem por inclinação a média
das inclinações das retas L1 e L2, ou seja, sua inclinação é:
f(xi , yi ) f(xi h, yi hy'i )
2
A reta L passa por (xi, yi) e é paralela à reta L0, donde:
f(xi , yi ) f(xi h, yi hy'i )
L : z(x) yi (x xi )
2
0011 0010
1
452

46.

L1
L0
y
P
yn 1 yn hy'n
L2
L
yn 1
y (x)
yn
xn
0011 0010
h
xn 1
1
452
x

47.

O valor fornecido para yi+1 pelo método de Euler Aperfeiçoado é:
h
yi 1 yi [f(xi ,yi ) f(xi h,yi hf ( xi , yi ) )], i 0,1, 2,... .
2
Observamos que este método é de passo um e só trabalha
com cálculos de f(x,y), não envolvendo suas derivadas. Assim,
para verificarmos que ele realmente é um método de Runge-
Kutta de 2ª ordem, falta verificar se sua fórmula concorda com a
do método de série de Taylor até os termos de 2ª ordem em h:
h2
h2
yi 1 yi hf ( xi , yi )
f x ( xi , yi )
f ( xi , yi ) f x ( xi , yi )
2
2
1
452
Esta verificação será feita para o caso geral, apresentado a
seguir.
0011 0010

48.

FORMA GERAL DOS MÉTODOS
DE
RUNGE-KUTTA DE 2ª ORDEM
0011 0010
1
452

49.

O método de Euler Aperfeiçoado é um método de Runge-Kutta
de 2ª ordem e podemos pensar que ele pertence a uma classe
mais geral de métodos do tipo:
yi 1 yi ha1 f ( xi , yi ) ha2 f ( xi b1h, yi b2 hf ( xi , yi ))
Para o método de Euler Aperfeiçoado,
a1 1 2 b1 1
a2 1 2 b2 1
Temos quatro parâmetros livres: a1, a2, b1e b2. A concordância
1
452
com o método da série de Taylor até os termos de ordem h2 é
será mostrado a seguir.
0011 0010

50.

O desenvolvimento de Taylor da função f(xi + b1h, yi + b2hf(xi , yi ))
em torno do ponto (xi , yi ) é dado por:
f ( xi b1h, yi b2 hf ( xi , yi )) f ( xi , yi ) b1hf x ( xi , yi ) b2 hf ( xi , yi ) f y ( xi , yi )
+ termos de h2.
Desta forma o método de Runge-Kutta pode ser reescrito como:
yi 1 yi a1hf ( xi , yi ) a2 h[ f ( xi , yi ) b1hf x ( xi , yi ) b2 hf ( xi , yi ) f y ( xi , yi )]
+ termos de h3.
0011 0010
1
452

51.

A expressão:
yi 1 yi a1hf ( xi , yi ) a2 h[ f ( xi , yi ) b1hf x ( xi , yi ) b2 hf ( xi , yi ) f y ( xi , yi )]
+ termos de h3.
pode ser escrita como
yi 1 yi a1hf ( xi , yi ) a2 hf ( xi , yi ) a2b1h2 f x ( xi , yi ) a2b2h2 f ( xi , yi ) f y ( xi , yi )
+ termos de h3.
yi 1 yi hf ( xi , yi )(a1 a2 ) h2 [a2b1 f x ( xi , yi ) a2b2 f ( xi , yi ) f y ( xi , yi )]
+ termos de h3.
0011 0010
1
452

52.

Como o método de série de Taylor de 2ª ordem é escrita como:
yi 1 yi h f ( xi , yi ) h 2
1
[ f x ( xi , yi ) f y ( xi , yi ) f ( xi , yi )], i 0,1, ...
2
+ termos de h3.
E o método de Runge-Kutta de 2ª ordem é dado por:
yi 1 yi h f ( xi , yi )(a1 a2 ) h2 [a2b1 f x ( xi , yi ) a2b2 f ( xi , yi ) f y ( xi , yi )]
+ termos de h3.
Então, a concordância dos dois métodos até h2 é obtida se:
a1 a2 1
a2b1 1 2
a b 1
2
2 2
0011 0010
1
452

53.

O sistema anterior possui três equações e quatro variáveis.
Escolhendo um dos parâmetros arbitrariamente, por exemplo
a2=w ≠ 0, temos:
a1 a2 1
a2b1 1 2
a b 1
2
2 2
a1 1 w
1 w
b
b
1 2 2
e a forma mais geral dos métodos de Runge-Kutta de 2ª ordem é
dada por
yi 1 yi h[(1 w) f ( xi , yi ) wh[ f ( xi 2hw , yi 2hw f ( xi , yi ))], i 0,1, 2, ...
0011 0010
1
452

54.

MÉTODOS DE RUNGE-KUTTA
DE
ORDENS SUPERIORES
0011 0010
1
452

55.

De forma análoga, pode-se construir métodos de 3ª ordem, 4ª
ordem, etc. A seguir serão fornecidas apenas fórmulas para
métodos de Runge-Kutta de 3ª e 4ª ordem:
3ª ordem
2
1
4
yi 1 yi k1 k 2 k3 onde
9
3
9
k1 hf ( xi , yi )
h
k1
k 2 hf ( xi , yi )
2
2
3
3
k3 hf ( xi h, yi k 2 )
4
4
0011 0010
1
452

56.

4ª ordem
2
1
4 onde
yi 1 yi k1 k 2 k3
9
3
9
k1 hf ( xi , yi )
h
k1
k 2 hf ( xi , yi )
2
2
3
3
k3 hf ( xi h, yi k 2 )
4
4
0011 0010
1
452

57.

OBSERVAÇÃO:
Os métodos de Runge-Kutta, apesar de serem autoiniciáveis (pois são de passo um) e não trabalharem com
derivadas de f(x,y), apresentam a desvantagem de não
haver para eles uma estimativa simples para o erro, o que
inclusive poderia ajudar na escolha do passo h.
Existem ainda adaptações dos métodos de Runge-Kutta que
são simples operacionalmente e que são usadas também
para estimativas de erro e controle do tamanho do passo h.
0011 0010
1
452

58.

MÉTODOS DO PONTO
MÉDIO
0011 0010
1
452

59.

Considere agora o desenvolvimento de y(xi + h) e y(xi − h) em
série de Taylor em torno do ponto xi, isto é:
h2
h3
y" ( xi )
y ' ' ' ( xi ) .
y ( xi h) y ( xi ) hy ' ( xi )
2!
3!
2
3
h
h
y ( x h) y ( x ) hy ' ( x )
y" ( xi ) y ' ' ' ( xi ) .
i
i
i
2!
3!
Fazendo
y( xi h) y( xi h)
obtemos:
3
h
y ( xi h) y ( xi h) 2hy ' ( xi ) y ' ' ' ( xi ) .
3!
O ( h3 )
0011 0010
1
452

60.

Considerando apenas o primeiro termo do lado direito da
expansão acima, substituindo y(xi+h) por yi+1, y(xi − h) por yi−1 e
y’(xi) por fi, obtemos:
yi 1 yi 1 2hf i
ou
yi 1 yi 1 2hf i
onde y0 e y1 são valores iniciais.
1
452
Desta forma o método do ponto médio é de passo dois e
possui ordem 2.
0011 0010

61.

Série de Taylor:
Seja f uma função com derivadas de todas as ordens em algum
intervalo contendo a como um ponto interior. Então, a série de
Taylor gerada por f em x = a é
k 0
f ( k ) (a)
f ´´(a)
f ( n ) (a)
k
2
( x a) f (a) f ´(a)( x a)
( x a) ...
( x a) n ...
k!
2!
n!
0011 0010
1
452

62.

Exemplo:
Desenvolver f(x) = ln(x) , em torno de x = 1.
f ( x) ln x f (1) 0
f ' ( x) x 1 f ' (1) 1
f ' ' ( x) x 2 f ' ' (1) 1
f ' ' ' ( x) 2 x 3 f ' ' ' (1) 2
f IV ( x) 6 x 4 f IV (1) 6
f n ( x) ( 1) n 1 (n 1)! x n f n (1) ( 1) n 1 (n 1)!
Assim,
1
452
( x 1) 2 2( x 1)3 6( x 1) 4
( 1) n 1 (n 1)!( x 1) n
ln x 0 ( x 1)
...
...
2!
3!
4!
n!
0011 0010

63.

Portanto,
( x 1) 2 ( x 1)3 ( x 1) 4
( 1) n 1 ( x 1) n
ln x ( x 1)
...
...
2
3
4
n
0011 0010
1
452

64.

MÉTODOS DE PASSO MÚLTIPLO
BASEADOS EM INTEGRAÇÃO
NUMÉRICA
0011 0010
1
452

65.

A característica destes métodos é a utilização de
informações sobre a solução em mais de um ponto. Podem ser
divididos em:
Métodos explícitos: trabalha-se com as aproximações yi, yi-1,
yi-2, ..., yi-m para obter yi+1.
Métodos implícitos: trabalha-se com as aproximações yi+1, yi, yi1,
0011 0010
yi-2, ..., yi-m para obter yi+1.
1
452

66.

A fórmula geral dos métodos lineares de passo múltiplo
é dada por:
yi 1
k
j 1
j
yi j 1 h
k
j 0
j
f i j 1 ;
i k 1
Nesta expressão, observa-se que:
Se β0 = 0, são necessários k passos anteriores: yi, yi-1, yi-2, ...,
yi-(k-1). Este é um método explícito.
1
452
Se β0 ≠ 0, necessita-se de k passos anteriores e do valor de
fi+1 = f(xi+1, yi+1). Este é um método implícito.
0011 0010

67.

MÉTODO DE ADAMS BASHFORTH
0011 0010
1
452

68.

Estes métodos baseiam-se na idéia de integrar a
equação diferencial ordinária de primeira ordem, isto é:
y ' ( x) f x , y ( x)
xi 1
y ' ( x) dx
xi
y ( xi 1 ) y ( xi )
xi 1
f x , y( x) dx
xi
xi 1
f x , y( x) dx
xi
y ( xi 1 ) y ( xi )
xi 1
f x , y( x) dx
xi
0011 0010
1
452

69.

Seja a aproximação de f(x, y(x)) dada pelo polinômio de
grau m, pm(x) , que interpola f(x, y(x)) em:
xi , xi 1 , xi 2 , , xi m . (Método explícito)
xi 1 , xi , xi 1 , xi 2 , , xi ( m 1) .(Método implícito)
Desta forma, a expressão
BASHFORTH são do tipo:
yi 1 yi
dos
métodos
de
ADAMS
–
xi 1
pm ( x) dx
xi
0011 0010
1
452

70.

Para m = 3, mostra-se que:
Método explícito de ordem 4
yi 1
h
55 f i 59 f i 1 37 f i 2 9 f i 3
yi
24
para i 3
com erro local:
251 5 (5)
eloc ( xi 1 )
h y ( xi )
720
0011 0010
,
x [ xi , xi 1 ]
i
1
452

71.

Para m = 3, mostra-se que:
Método implícito de ordem 4
yi 1 y i
h
9 f i 1 19 f i 5 f i 1 f i 2
24
para i 2
com erro local:
eloc ( xi 1 )
19 5 (5)
h y ( xi )
720
,
x [ xi , xi 1 ]
i
Aconselha-se a utilização de um método de passo simples
de mesma ordem para a obtenção dos valores necessários para a
1
452
inicialização do método de passo múltiplo. Nesse caso, é usual
aplicar o Método de Runge-Kutta de quarta ordem.
0011 0010

72.

MÉTODO PREDITOR – CORRETOR
DE ADAMS-MOULTON
0011 0010
1
452

73.

Dado o PVI:
y ' f ( x, y )
y ( xo ) y o
1o passo: Calcular usando um método de passo simples de 4ª
ordem os valores iniciais: y1
2o passo:
, y 2 e y3
Calcular yi+1(0) utilizando o método explícito
(PREVISÃO):
yi( o1) yi
0011 0010
h
55 f i 59 fi 1 37 f i 2 9 f i 3
24
i 3
1
452

74.

3o passo: Calcular:
fi( o1) f ( xi 1, yi( o1) )
4o passo: Calcular yi+1(k) utilizando o método implícito
(CORREÇÃO):
y
(k )
i 1
h
yi
9 f i (1k 1) 19 f i 5 f i 1 f i 2
24
Até que
yi( k1) yi( k1 1)
(k )
yi 1
0011 0010
k 1,2,3,..
1
452

75.

EQUAÇÃO DIFERENCIAL DE
ORDEM M
0011 0010
1
452

76.

Uma equação diferencial de ordem m, pode ser reduzida
a um sistema de m equações de primeira ordem. A maneira mais
usual para resolver estas m equações, desde que seja um PVI, é
trabalhar na forma matricial.
Para exemplificar, consideremos uma e.d.o. de 2ª ordem:
y" f ( x, y, y ' )
y ' ( xo ) y ' o , y ( xo ) y o
, seja
z ' f ( x, y , z )
z y ' e z ' y" y ' z
z( x ) y' , y( x ) y
o
o
o
o
escrevendo na forma matricial vem:
'
1
452
y' o
z f ( x, y , z )
Y ' F x, Y para Y ( xo )
y
z
yo
0011 0010

77.

A equação diferencial
Y ' F x, Y
y' o
para Y ( xo )
yo
pode ser resolvida utilizando qualquer um dos métodos estudados
anteriormente. Por exemplo, o método de Euler Aperfeiçoado:
Yi 1
0011 0010
h
Yi
F ( xi , Yi ) F xi h , Yi h Yi '
2
1
452