Similar presentations:
Математическая экономика. Общее равновесие. (Тема 5)
1. Математическая экономика
Тема 5. ОБЩЕЕ РАВНОВЕСИЕМатематическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
2. 5.1. Виды и объекты равновесных моделей
5.1. ВИДЫ И ОБЪЕКТЫРАВНОВЕСНЫХ МОДЕЛЕЙ
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
3. Равновесные модели подразделяются на модели: - частичного, - полирынкового (англ. multi-market) - общего равновесия
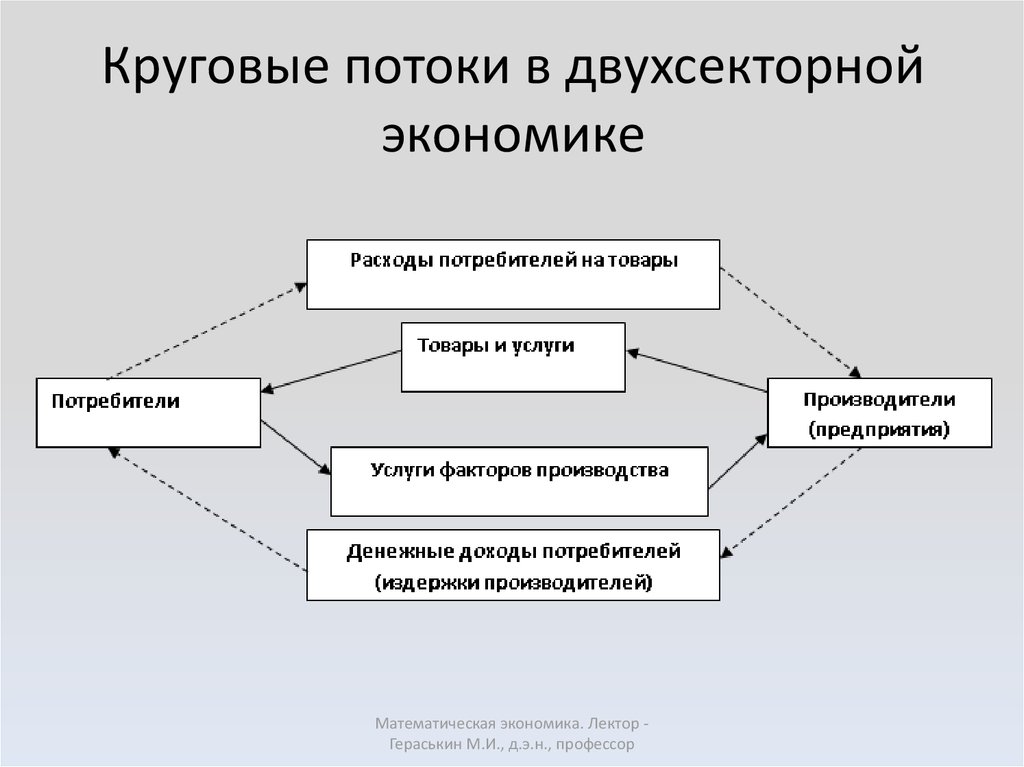
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор4. Круговые потоки в двухсекторной экономике
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор5. 5.2. Простой обмен в двухсубъектной двухпродуктовой экономике
5.2. ПРОСТОЙ ОБМЕН ВДВУХСУБЪЕКТНОЙ
ДВУХПРОДУКТОВОЙ ЭКОНОМИКЕ
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
6. Экономика состоит из двух субъектов, А и В, изначально имеющих два товара, X и Y, в количествах (Х0А, Y0A) и (Х0В, Y0В).
Кривая предложения из запасаБюджетное уравнение для одного из субъектов :
px
I
Y
X
py py
где I – бюджет субъекта А;
px и py – цены (идеальные) товаров.
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
(5.1)
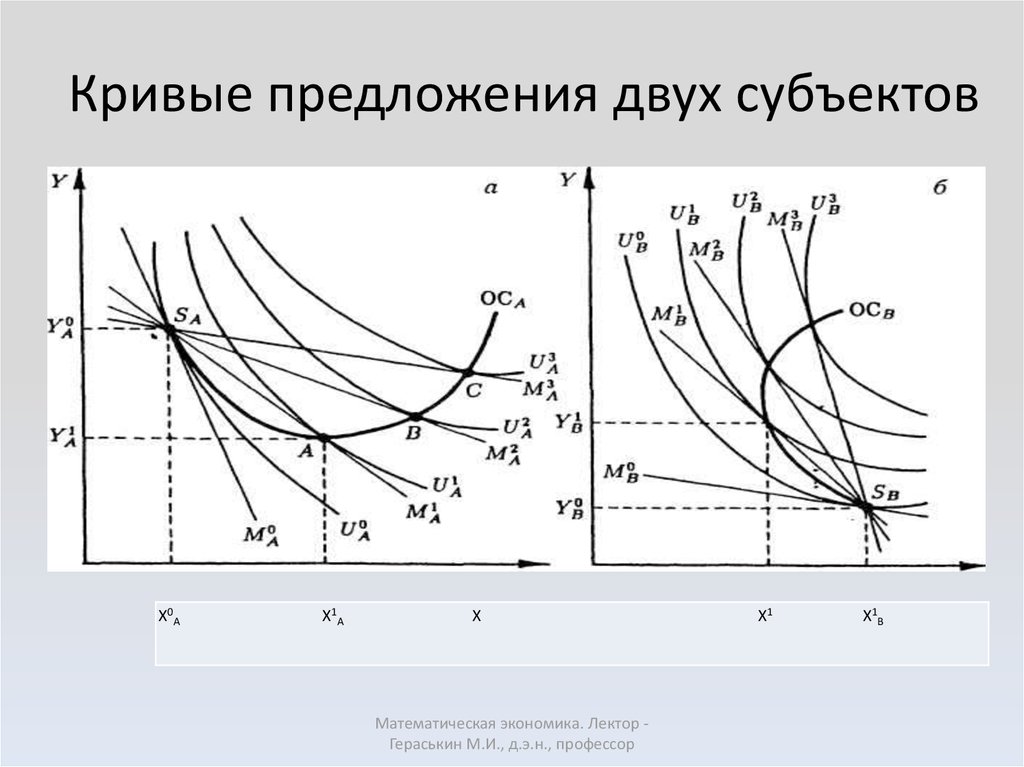
7. Кривая предложения ОСA товара Y из его начального запаса Y0А к обмену на товар X (ОС; offer curve — англ.) представляет собой множество точек (SA, А, B,
Кривая предложения ОСA товара Y изего начального запаса Y0А к обмену на
товар X (ОС; offer curve — англ.)
представляет собой множество точек
(SA, А, B, С, ...) касания кривых
безразличия и бюджетных линий,
проходящих через точку начального
запаса и имеющих разный наклон.
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
8. Экономически кривая предложения из запаса показывает количество второго товара, до которого готов довести свой запас потребитель при раз
Экономически кривая предложенияиз запаса показывает количество
второго товара, до которого готов
довести свой запас потребитель при
различных соотношениях цен
товаров.
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
9. Получим выражение кривой предложения из запаса, учитывая, что для неё, во-первых, выполняется условие оптимального потребительского выбор
Получим выражение кривой предложения иззапаса, учитывая, что для неё, во-первых,
выполняется условие оптимального
потребительского выбора:
MU x px
MU y p y
(5.2)
и, во-вторых, она соединяет бюджетные линии,
проходящие через некоторую точку:
px
0
Y Y
X X
py
0
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
(5.3)
10. Выразив соотношение цен товаров из (5.3), , и подставив в (5.2), получим:
Y Y 0px
X X
0
py
MU x
Y Y0
MU y X X 0
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
(5.4)
11. Кривые предложения двух субъектов
Х 0АХ 1А
X
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
Х1
Х1 В
12. Пример вывода выражения кривой предложения
Например, для степенной функции полезности видаU X Y
имеем следующее выражение кривой предложения:
Y Y0
Y
X X X 0
откуда
X Y Y0 Y X X 0
следовательно
Y0 X
Y
X X 0
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
13. Это уравнение определяет гиперболу, вертикальная асимптота (нуль знаменателя) которой имеет координату: а горизонтальная асимптота (по пр
Это уравнение определяет гиперболу,вертикальная асимптота (нуль
знаменателя) которой имеет координату:
X 0
X
а горизонтальная асимптота (по правилу
Лопиталя или как отношение
коэффициентов при старших степенях
дробно-рациональной функции) –
координату
Y0
Y
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
14. При этом предполагается, что , иначе товары равноценны для потребителя и обмена не происходит. Таким образом, для монотонной кривой безразл
При этом предполагается, что ,иначе товары равноценны для потребителя
и обмена не происходит. Таким образом,
для монотонной кривой безразличия,
характерной для степенной функции
полезности, кривая предложения из запаса
также монотонно убывает. Поэтому
участок SAOCA правее точки А на рис. 5.2 (а)
или левее точки В недопустим, так как это
означает «обратный» эффект замены.
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
15. 5.3. Анализ обмена в двухсубъектной двухпродуктовой экономике. Коробка Эджуорта
5.3. АНАЛИЗ ОБМЕНА ВДВУХСУБЪЕКТНОЙ ДВУХПРОДУКТОВОЙ
ЭКОНОМИКЕ.
КОРОБКА ЭДЖУОРТА
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
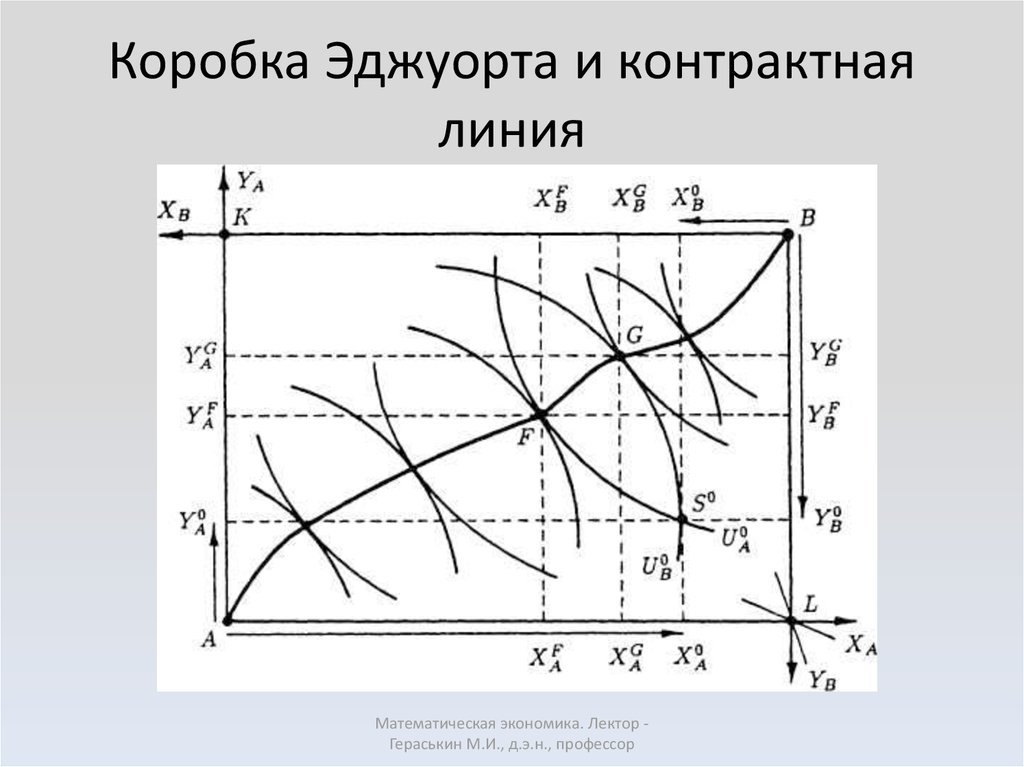
16. Коробка Эджуорта представляет совмещенные карты безразличия двух субъектов, А и В, причем карта безразличия В повернута на 180°.
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор17. Коробка Эджуорта и контрактная линия
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор18. Контрактная линия
Множество точек касания кривых безразличия двухсубъектов образует так называемую контрактную
линию (кривая АВ на рис. 5.3), характеризующую
множество взаимоприемлемых результатов обмена
двух субъектов.
Уравнение контрактной линии имеет вид:
A
x
A
y
MU yB
MU
MU
MU xB
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
(5.6)
19. Пример вывода выражения контрактной линии
Для степенных функций полезности субъектовU X Y
A
U X Y
B
имеем следующее выражение контрактной линии:
Y
X
B , откуда
A
X
Y
A
следовательно
B
Y L X
X K Y
Y 2 KY X 2 LX
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
20. Обозначив запишем это уравнение в виде:
Y KY X LX2
2
Это уравнение определяет семейство
функций Y=Y(X). Преобразуя к квадрату
разности левую и правую части уравнения,
получим:
2
K
К
X
L
L
Y
2
4
2
4
2
2
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
2
(5.7)
21. Рассмотрим частный случай потребителей, имеющих противоположные предпочтения , при этом
Рассмотрим частный случайпотребителей, имеющих
противоположные предпочтения , ,
при этом 1
2
2
K
К
L
L2
X
Y
2
4
2
4
2
Для случая равенства запасов K=L имеем:
Y X
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
(5.8)
22. Таким образом, контрактная линия является монотонно возрастающей (для степенных функций полезности при равенстве коэффициентов эластичн
Таким образом, контрактная линияявляется монотонно возрастающей
(для степенных функций полезности
при равенстве коэффициентов
эластичности и одинаковых запасах
товаров – линейно возрастающей).
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
23. Условия максимизации полезности
Максимальное удовлетворение (полезность) дляобоих субъектов возможно в точке касания кривых
безразличия субъектов, лежащей на бюджетной
линии, проходящей через точку начального запаса
товаров:
MRS
A
X ,Y
MRS
B
Y ,X
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
Px
Py
(5.9)
24. Пример определения равновесия в обмене
Выражение кривой предложения первого субъектаY0 X
Y
X X 0
получено выше (формула (5.5)). Выражение кривой
предложения второго субъекта найдем, подставив
в эту формулу координаты второй системы осей в
коробке Эджуорта
X B L X A , YB K YA
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
25. и заменив коэффициенты эластичности α на γ, β на δ. В результате получим:
K Y0 L XK Y
L X L X 0
Координаты точки равновесия определяем,
приравнивая выражение кривой предложения
первого субъекта и второго субъекта откуда
Y0 X
K Y0 L X
K
X X 0
L X L X 0
(5.10)
Полученное трансцендентное уравнение позволяет
определить искомый оптимальный товарный набор.
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
26. 5.4. Равновесие в производстве. Двухфакторная двухпродуктовая модель
5.4. РАВНОВЕСИЕ В ПРОИЗВОДСТВЕ.ДВУХФАКТОРНАЯ
ДВУХПРОДУКТОВАЯ МОДЕЛЬ
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
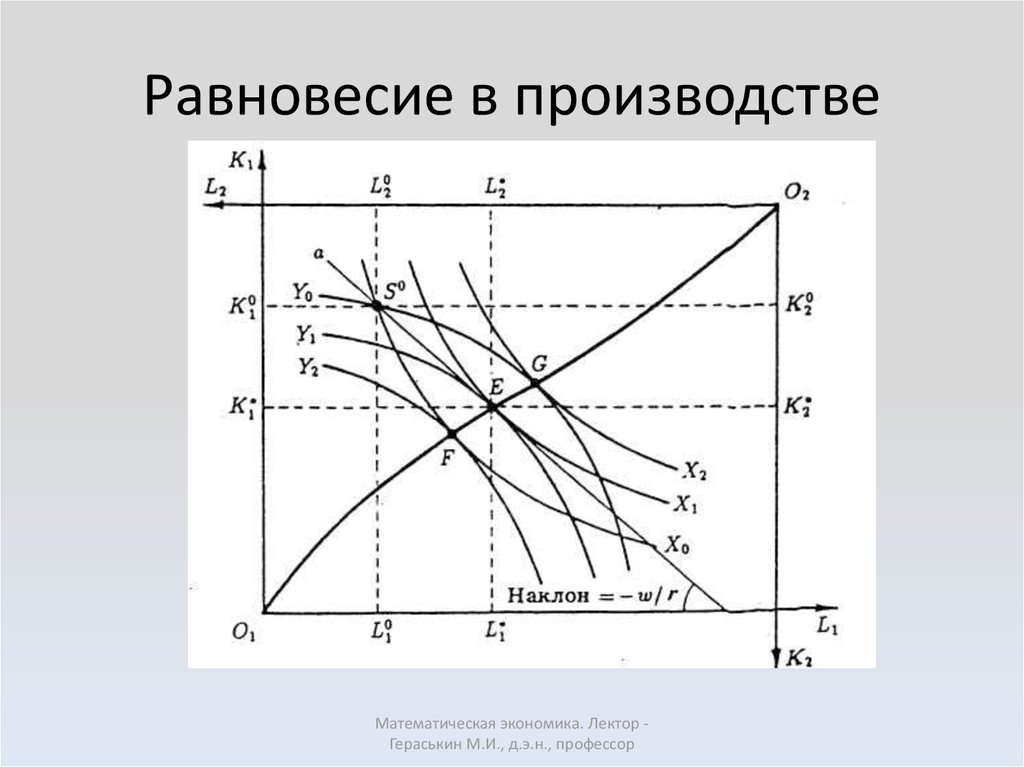
27. Уравнение контрактной линии при обмене производственными ресурсами имеет вид:
MRTSXKL = MRTSYKL .(5.11)
Равновесие при обмене производственными
ресурсами устанавливается при условии:
MRTS
X
KL
MRTS
Y
LK
w
r
(5.12)
где обозначены фактора производства, К и L,
приобретаемых по ценам w и r.
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
28. Равновесие в производстве
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор29. 5.5. Равновесие в производстве и потреблении
5.5. РАВНОВЕСИЕ ВПРОИЗВОДСТВЕ И ПОТРЕБЛЕНИИ
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
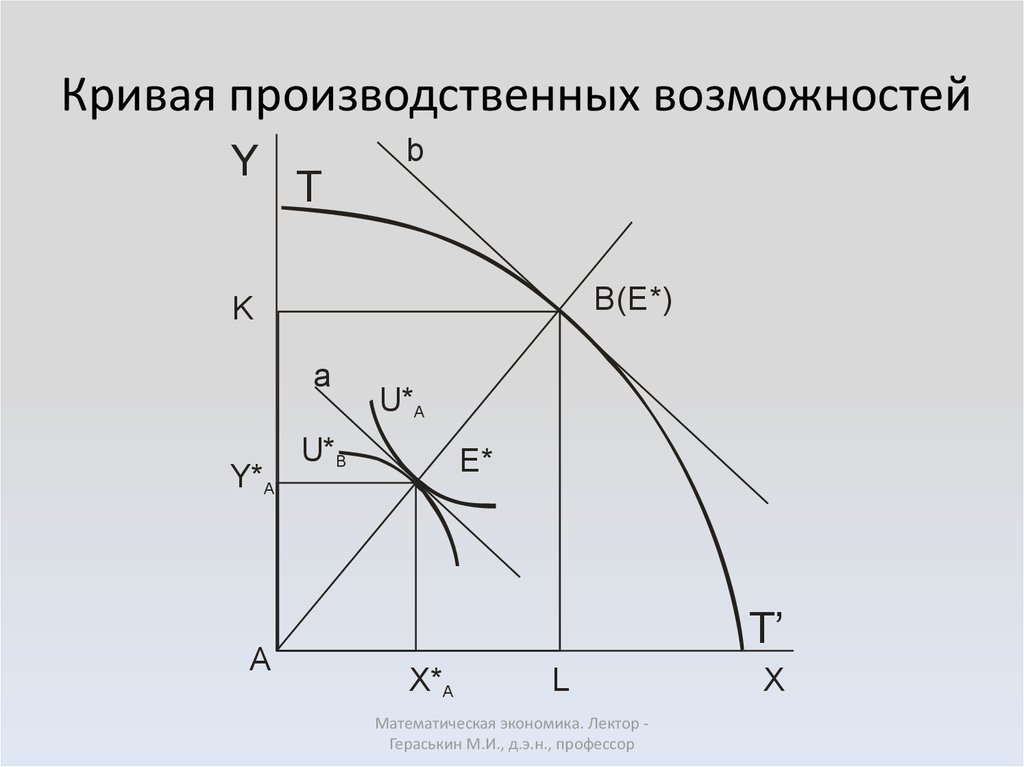
30. Кривая производственных возможностей (кривая продуктовой трансформации) характеризует все множество комбинаций максимальных выпусков д
Кривая производственныхвозможностей (кривая продуктовой
трансформации) характеризует все
множество комбинаций максимальных
выпусков двух товаров, X и Y, при
полном и эффективном использовании
наличных факторов производства, K и L .
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
31. Пример вывода формулы кривой производственных возможностей
Для производственных функций фирмX L K
Y L K
можно получить выражение кривой
производственных возможностей, если один из
ресурсов, например К, расходуется на выпуск
обоих продуктов:
X 1/
Y 1/
K X K Y / / K Const
LX
LY
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
(5.13)
32. Кривая производственных возможностей является эллиптической кривой, то есть прирост производства одного товара обусловливает снижение в
Кривая производственныхвозможностей является
эллиптической кривой, то есть
прирост производства одного товара
обусловливает снижение выпуска
другого товара, причем чем больше
выпускается первого товара, тем
значительнее сокращение другого
товара.
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
33. Предельная норма продуктовой трансформации (MRPT; marginal rate of product transformation — англ.) –показывает, на сколько должно быть сокращено производство
Предельная норма продуктовойтрансформации (MRPT; marginal rate of
product transformation — англ.) –показывает,
на сколько должно быть сокращено
производство товара Y для того, чтобы выпуск
товара X увеличился на единицу при
постоянных запасах ресурсов:
MRPTХY = –
dY
dX
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
34. Можно показать, что предельная норма продуктовой трансформации равна соотношению предельных издержек на каждый товар:
MRPTХY = –dY
= MCx
dX
MCy
(5.14)
Действительно, при постоянных запасах ресурсов
dK 0, dL 0
дифференциал издержек равен нулю:
C
C
dC
dX
dY 0
X
Y
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
35. Отсюда:
CdY X MC X
dX C MCY
Y
В условиях совершенной конкуренции цены равны
предельным издержкам:
MRPTХY = MCx = Px
(5.15)
MCy
Py
Поскольку правые части (5.15) и (5.9) одинаковы —
PX/PY, мы можем приравнять и левые их части, в
результате чего получим условие общего
равновесия:
MRPTХY = MRSAX,Y = MRSBX,Y .
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
36. Кривая производственных возможностей
YТ
b
B(E*)
K
a
Y*A
A
U*A
U*B
E*
Т’
X*A
L
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
X
37. Таким образом, в условиях совершенной конкуренции двух-субъектная, двухфакторная, двухпродуктовая экономическая система находится в сост
Таким образом, в условиях совершеннойконкуренции двух-субъектная, двухфакторная,
двухпродуктовая экономическая система находится
в состоянии общего равновесия, когда
выполняются следующие три условия:
1) Предельные нормы замены двух товаров
одинаковы для обоих субъектов и равны
соотношению их цен.
2) Предельные нормы технологической замены
факторов производства одинаковы для обеих фирм
и равны соотношению факторных цен.
3) Предельные нормы замены двух товаров в
потреблении одинаковы и равны предельной норме
продуктовой трансформации.
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
38. 5.6. Модель общего равновесия Вальраса
5.6. МОДЕЛЬ ОБЩЕГОРАВНОВЕСИЯ ВАЛЬРАСА
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
39. Функция спроса на товар является функцией цен всех т товаров:
QDi=Di(P1,...,Pi,...,Pm), i=1,2,...,т.(5.17)
На совершенно конкурентном рынке
предложение товара также является
функцией цен всех т товаров:
QSi=Si(P1,...,Pi,...,Pm), i = 1,2,.:,m.
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
(5.18)
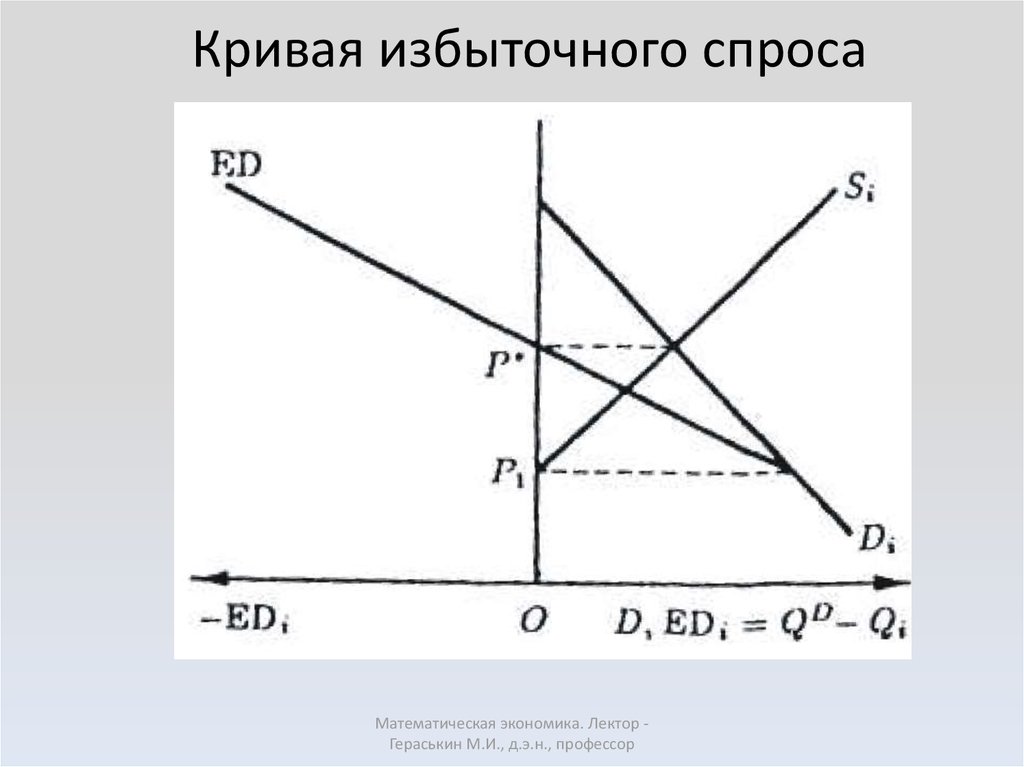
40. Функция избыточного спроса (ED; excess demand — англ.) на товар может быть представлена как разность между функцией спроса и функцией предложения:
EDi(P1,…Pi,…Pm)= Di(P1,...P,i...Pm)-Si(Pl,...,Pi,...,Pm).(5.19)
Условием равновесия на рынках – равенство
избыточного спроса нулю:
EDi (P1,...,Pm) = 0.
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
(5.20)
41. Кривая избыточного спроса
Кривая избыточного спросаМатематическая экономика. Лектор Гераськин М.И., д.э.н., профессор
42. Условие «расчистки рынка» - для экономики в целом общая ценность покупок всегда равна общей ценности продаж, и, значит,
mP ED ( P ,..., P
i
i
1
m
) 0
(5.21)
i
Равенство (5.21) интерпретируют обычно как закон
Вальраса: если все рынки, кроме одного, т. е. т-1
рынков, находятся в равновесии, то и оставшийся
(т-1)-й рынок также находится в равновесии. А это
значит, что число независимых уравнений в системе
равно т - 1.
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
43. Разделим все цены на Р1. Тогда (5.21) примет вид
EDi ( 1, , ,..., PmP1 ) 0
P2
P1
P3
P1
(5.22)
Таким образом, мы получили систему,
состоящую из т – 1 уравнения,
допускающую единственное решение
относительно (т - 1 )-й цены.
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
44. Пример условий равновесия для линейных функций спроса и предложения
При функциях спроса и предложенияQD =A-aP и QS =В + bР
функцией избыточного спроса будет
ЕQ =(А-В)-(а + b)Р.
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
45. Для рынка двух товаров условие (5.20) имеет вид:
A1 B1 a1 b1 p1 ,A2 B2 a2 b2 p2 ,
откуда, разделив первое уравнение на
второе, получим
A2 B2 a2 b2 p2
A1 B1 a1 b1 p1
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор
46. Приняв цену первого товара в качестве единицы счета, обозначим
p2p '2
p1
Поэтому можно записать уравнение Вальраса (5.22):
A2 B2 a2 b2
p '2
A1 B1 a1 b1
(5.23)
Условие «расчистки рынка» (5.21) имеет следующий вид:
p1 A1 B1 a1 b1 p1 p2 A2 B2 a2 b2 p2 0
Уравнения (5.23), (5.24) позволяют найти искомые
цены товаров.
Математическая экономика. Лектор Гераськин М.И., д.э.н., профессор








































 mathematics
mathematics economics
economics








