6_Ориентированные_и_неориентированные_взвешенные_графы

1. Ориентированные и неориентированные взвешенные графы

2. Введение

3.

4. Неориентированные взвешенные графы: Свойства и примеры

5. Ориентированные взвешенные графы: Свойства и примеры

6. Виды взвешенных графов: Полные, двудольные, циклические

Двудольные графы
• Двудольный граф — это граф,
вершины которого можно
разделить на два
непересекающихся множества
(доли) таким образом, что
каждое ребро соединяет
вершину из одной доли с
вершиной из другой доли.
Внутри одной доли рёбер нет.
Взвешенные двудольные
графы используются для
моделирования задач
сопоставления или назначения,
например, распределение задач
между сотрудниками или
сопоставление пользователей с
продуктами на основе
предпочтений, где веса могут
указывать на предпочтения
или эффективность.
Циклические графы
• Циклический граф (или граф
с циклами) — это граф,
который содержит хотя бы
один цикл, то есть путь,
начинающийся и
заканчивающийся в одной и
той же вершине. Взвешенные
циклические графы
встречаются во многих
областях, например, в
анализе финансовых
транзакций (поиск
арбитражных циклов), в
транспортных сетях
(оптимизация круговых
маршрутов). Наличие циклов
в взвешенных графах может
влиять на алгоритмы поиска
кратчайших путей, особенно
при наличии отрицательных
весов.

7. Методы формального описания графов: Матрица смежности

8. Методы формального описания графов: Матрица смежности

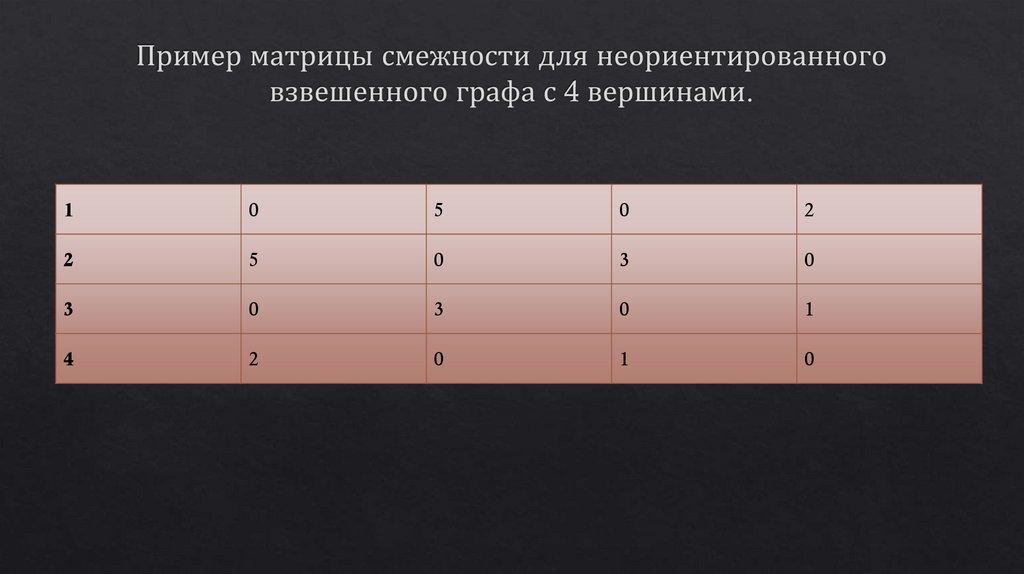
9. Пример матрицы смежности для неориентированного взвешенного графа с 4 вершинами.

1
0
5
0
2
2
5
0
3
0
3
0
3
0
1
4
2
0
1
0

10. Методы формального описания графов: Матрица инцидентности

11. Методы формального описания графов: Матрица инцидентности

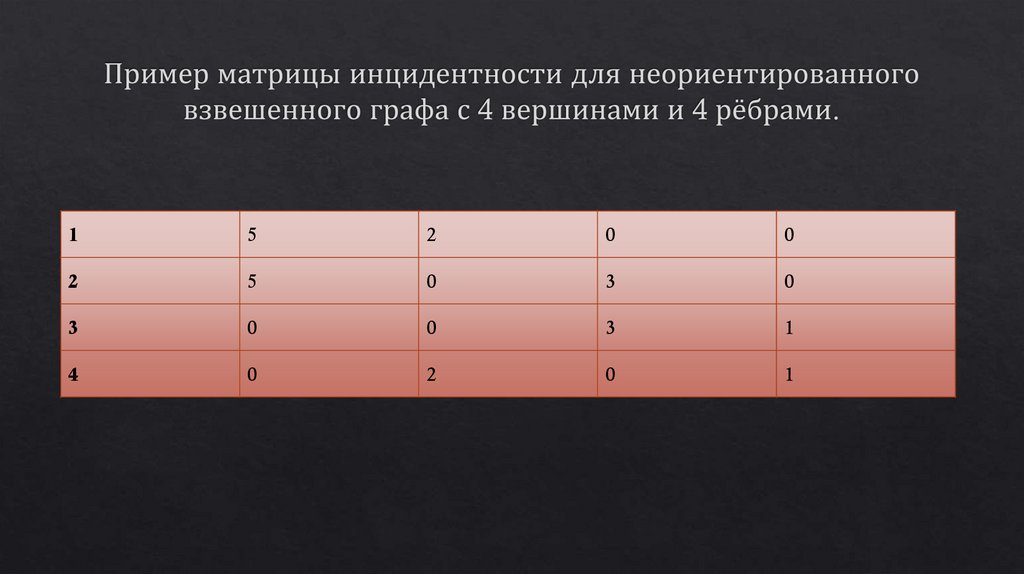
12. Пример матрицы инцидентности для неориентированного взвешенного графа с 4 вершинами и 4 рёбрами.

1
5
2
0
0
2
5
0
3
0
3
0
0
3
1
4
0
2
0
1