Kvadratnye-funkcii-Neozhidannye-geroi-povsednevnosti.pptx

1.

Квадратные функции:
Неожиданные герои
повседневности
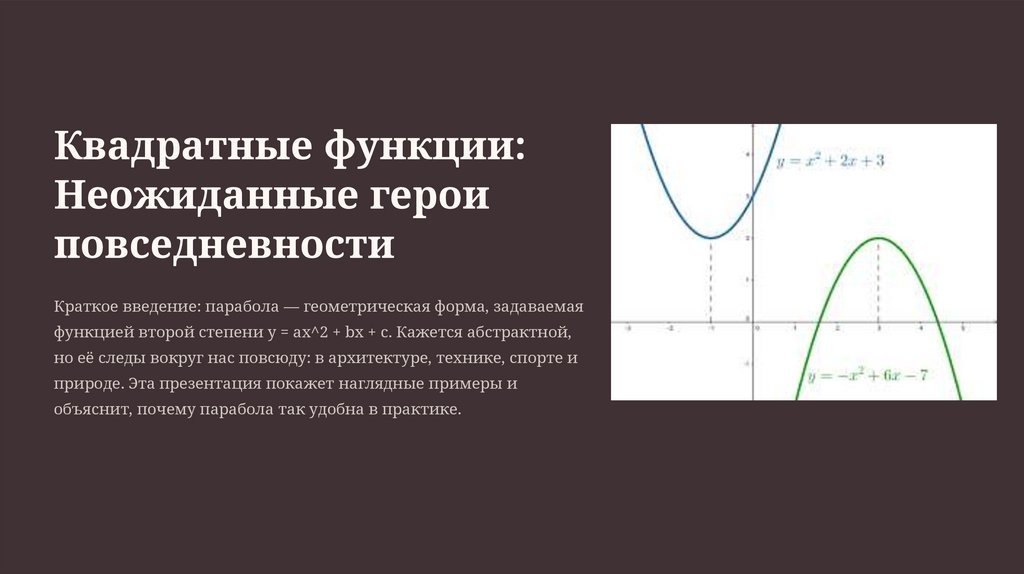
Краткое введение: парабола — геометрическая форма, задаваемая
функцией второй степени y = ax^2 + bx + c. Кажется абстрактной,
но её следы вокруг нас повсюду: в архитектуре, технике, спорте и
природе. Эта презентация покажет наглядные примеры и
объяснит, почему парабола так удобна в практике.

2.

Парабола на ладони: от фонтанов до спутниковых
антенн
Рассмотрим фонтан, изображённый на фото. Центральная струя воды
поднимается вверх и её движение можно описать с помощью
квадратичной функции:
( h(t) = -4t^2 + 16t ),
где ( h(t) ) — высота струи в метрах, а ( t ) — время в секундах с момента
вылета воды.
Найдём основные характеристики движения струи.
Сначала определим, через сколько секунд вода достигнет
максимальной высоты. Для квадратичной функции вида ( at^2 + bt + c ) Архитектура
вершина параболы находится по формуле
( t = -b\2a ).
Арки и пролёты
В нашем случае ( a = -4 ), ( b = 16 ). Подставляем:
часто проектируют с
( t = -16\2(-4) = -16\-8 = 2 ).
Фонтан
Значит, максимальная высота достигается через 2 секунды.
параболическими
Теперь найдём саму максимальную высоту. Подставим ( t = 2 ) в
ы
Водные струи часто
формулу:
очертаниями —
(
h(2)
=
-4(2^2)
+
16
\
2
)
проектируют как
( h(2) = -4 \4 + 32 )
распределение
параболы: это красиво
( h(2) = -16 + 32 = 16 ).
Максимальная высота струи равна 16 метров.
нагрузок и эстетика
и предсказуемо —
Далее определим, сколько времени вода находится в воздухе. Для этого
сочетаются в
приравняем высоту к нулю:
одинаковая высота и
( -4t^2 + 16t = 0 ).
устойчивой форме.
форма струй при
Вынесем ( t ) за скобки:
( t(-4t + 16) = 0 ).
заданной начальной
Получаем два решения: ( t = 0 ) (момент вылета) и
( -4t + 16 = 0 t = 4 ).
скорости.
Следовательно, вода находится в воздухе 4 секунды.
Итак, струя достигает максимума через 2 секунды, поднимается на
высоту 16 метров и полностью падает обратно через 4 секунды.

3.

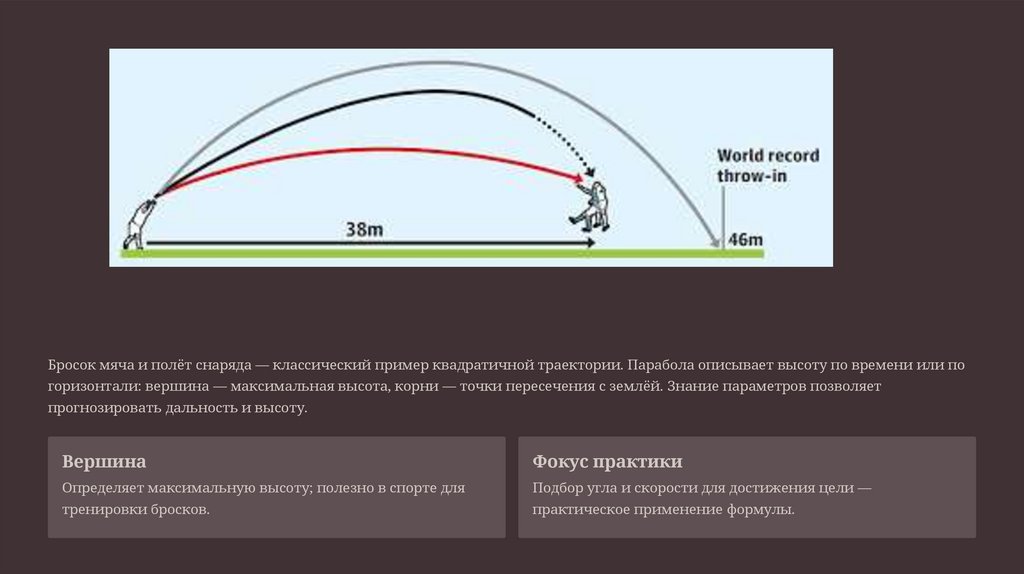
Бросок мяча и полёт снаряда — классический пример квадратичной траектории. Парабола описывает высоту по времени или по
горизонтали: вершина — максимальная высота, корни — точки пересечения с землёй. Знание параметров позволяет
прогнозировать дальность и высоту.
Вершина
Фокус практики
Определяет максимальную высоту; полезно в спорте для
Подбор угла и скорости для достижения цели —
тренировки бросков.
практическое применение формулы.

4.

Оптимизация и эффективность: где ещё встречаются функции
2-й степени?
Функции второй степени появляются в
задачах оптимизации: минимизация
затрат, максимизация прибыли, подбор
рецептуры. Простой пример —
минимизация общей длины материала при
заданной площади упаковки ведёт к
квадратным уравнениям.
Экономика
Инженерия
Фотография
Кривые затрат и прибыли часто имеют
квадратичные приближения при
небольших отклонениях.
Оптимизация формы и распределения
напряжений использует квадратичные
модели.
Модели резкости и глубины резко
зависят от квадратичных
приближений в оптике.

5.

За пределами математики: как понимание функций 2-й степени
меняет мир вокруг нас
Понимание квадратичных функций даёт практические инструменты: предсказывать траектории, проектировать формы,
оптимизировать процессы. Это сочетание интуиции (форма параболы) и формул (вершина, фокус, корни) помогает принимать точные
инженерные и повседневные решения.
Образование
Наглядные примеры делают абстракцию полезной и понятной —
от физики до дизайна.
Дизайн и технологии
Параболы используются для управления светом, звуком и
сигналами — улучшая эффективность систем.
Ключевая мысль: парабола — не просто формула. Это практический инструмент, который делает сложные задачи интуитивно
понятными и управляемыми.