КРИ1

1.

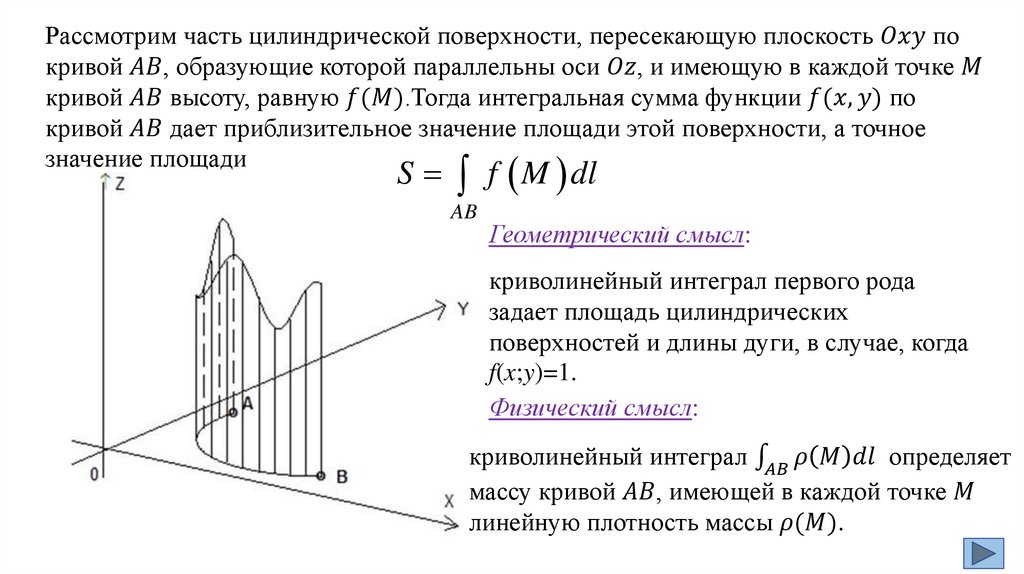
§ 1. Криволинейные интегралы 1-го рода, их
свойства и вычисление
Предположим, что на плоскости Оху задана гладкая кривая L, т. е. кривая, в каждой
точке M(x, у) которой определена касательная к этой кривой.
Произвольным образом осуществим n-разбиение кривой L на n частей (дуг):
L L1 L2 ... Ln
где частичные дуги могут соприкасаться, разве лишь, своими концами, т. е. длина
общей части Li L j , i j , равна нулю.
Пусть далее на кривой L задана некоторая скалярная функция f(x,y), (x,y) ∈ L
На каждой из полученных дуг Li длиною Δℓi произвольно выберем точку Mi*(ξi;ηi) и
составим интегральную сумму первого рода: n
1n f i ; i i
i 1
Обозначим через λ наибольшую из длин частичных дуг Li – диаметр разбиения:
max i max Li .
1 i n
1 i n

2.

Если существует конечный предел
B
интегральных сумм σn1 когда число
элементарных дуг, полученных при
разбиении, стремится к бесконечности
n→+∞ и при этом λ→0 и этот предел
не зависит как от способа разбиения
кривой L на части Li , так и от выбора
точек Mi*, то такой предел называется
КРИ-1 – криволинейным интегралом
x первого рода – интегралом по длине
дуги от функции f(x,у) по кривой L и
обозначается
y
Mi
yi
Li
yi
yi 1
M i* i , i
M i 1
xi
O
xi 1
xi
A
n
I lim f i , i i f M dl f ( x, y )d
n i 1
0
L
L

3.

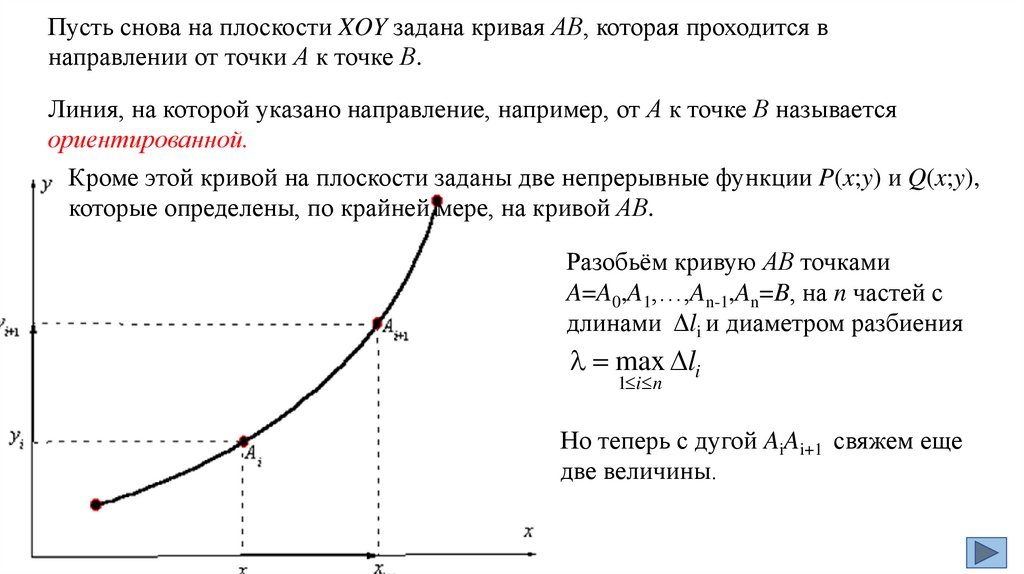
При этом функция f(x;y) называется интегрируемой вдоль кривой L, сама кривая –
дугой интегрирования, точка А — начальной, а точка В — конечной точками
интегрирования, dl — элемент кривой (дуги).
Теорема. Если функция f(x;y) непрерывна в каждой точке кривой L, и кривая L
гладкая (в каждой точке существует касательная к кривой и положение ее
непрерывно меняется при перемещении точки по кривой), то КРИ-1 существует.
В дальнейшем считаем, что кривая L является гладкой и для таких кривых имеет
место
(d ) (dx) (dy )
2
2
2
«теорема Пифагора для дифференциалов»: квадрат дифференциала длины дуги
равен сумме квадратов дифференциалов координат.
3

4.

Рассмотрим часть цилиндрической поверхности, пересекающую плоскость