Системы двух линейных уравнений с двумя переменным (1)

1.

Решение систем двух
линейных уравнений
с двумя
переменными
Алгебра 8 класс

2.

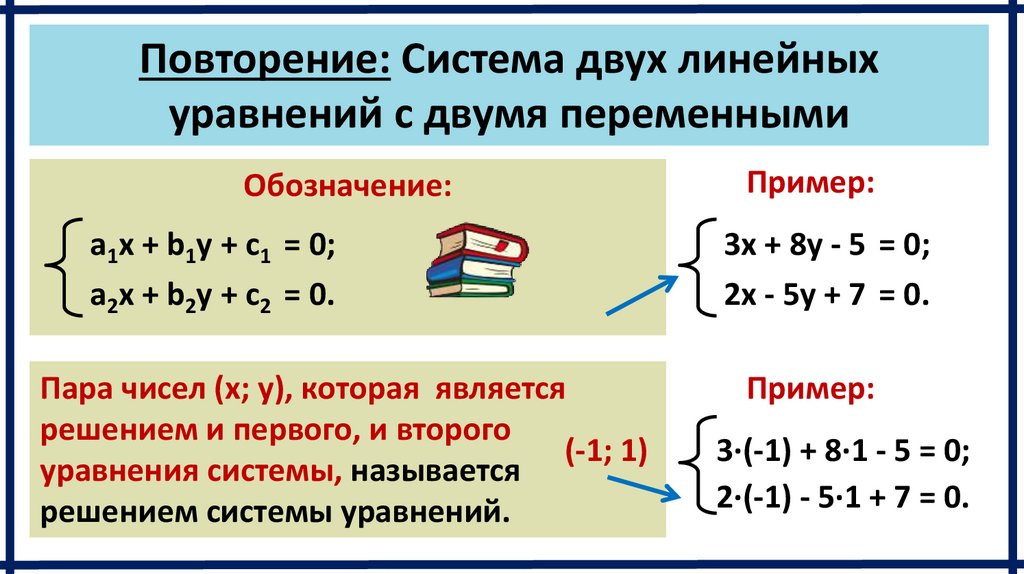
Повторение: Система двух линейных
уравнений с двумя переменными
Обозначение:
a1x + b1y + c1 = 0;
a2x + b2y + c2 = 0.
Пара чисел (x; y), которая является
решением и первого, и второго
(-1; 1)
уравнения системы, называется
решением системы уравнений.
Пример:
3x + 8y - 5 = 0;
2x - 5y + 7 = 0.
Пример:
3∙(-1) + 8∙1 - 5 = 0;
2∙(-1) - 5∙1 + 7 = 0.

3.

Повторение: Метод подстановки
Алгоритм:
1. Выразить одну переменную через
другую, например, y через x из первого
уравнения и подчеркнуть выражение.
2. Подставить полученное выражение
во второе уравнение вместо y.
3. Найти из полученного уравнения x.
4. Подставить полученное значение x в
выражение , равное y.
5. Записать в ответ пару чисел (x; y).
Пример:
-2x + y - 5 = 0;
-4x + 3y -1 = 0.
y = 2x + 5;
-4x + 3(2x + 5) - 1 = 0.
y = 2x + 5;
x = -7.
y = -9;
x = -7.

4.

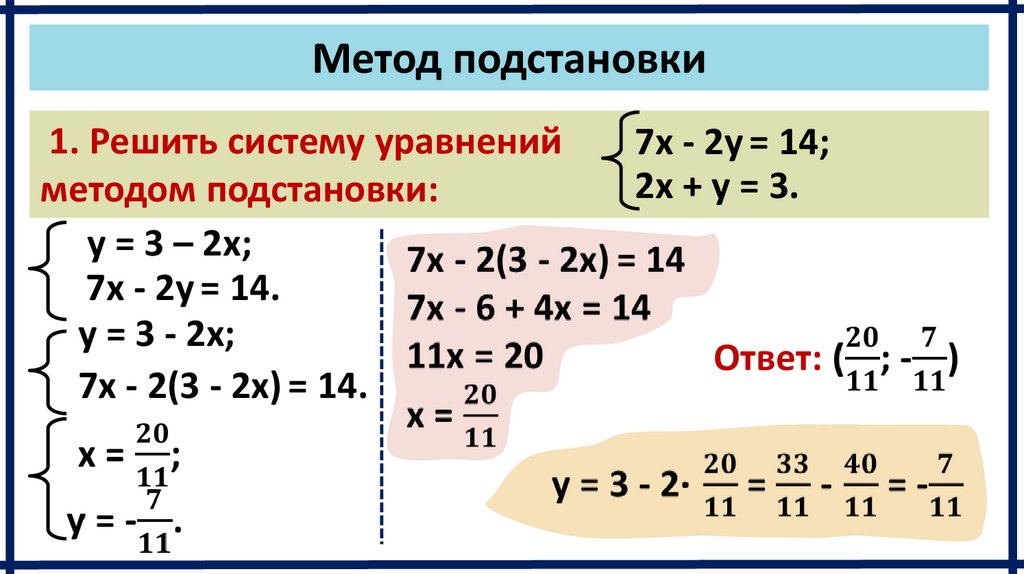
Метод подстановки
1. Решить систему уравнений
методом подстановки:
y = 3 – 2x;
7x - 2y = 14.
y = 3 - 2x;
7x - 2(3 - 2x) = 14.
7x - 2y = 14;
2x + y = 3.

5.

Повторение: Метод алгебраического сложения
Пример:
4x + 3y = 1;
Алгоритм:
1. Уравнять коэффициенты, например,
2x - y = 3.
при x (можно и при y).
4x + 3y = 1;
2. Сложить или вычесть уравнения.
+
3. Найти из полученного уравнения y.
6x - 3y = 9.
4. Подставить полученное значение y в
10x = 10; x = 1.
любое уравнение системы и найти x.
x = 1;
x = 1;
5. Записать в ответ пару чисел (x; y).
2∙1 - y = 3.
y = -1.

6.

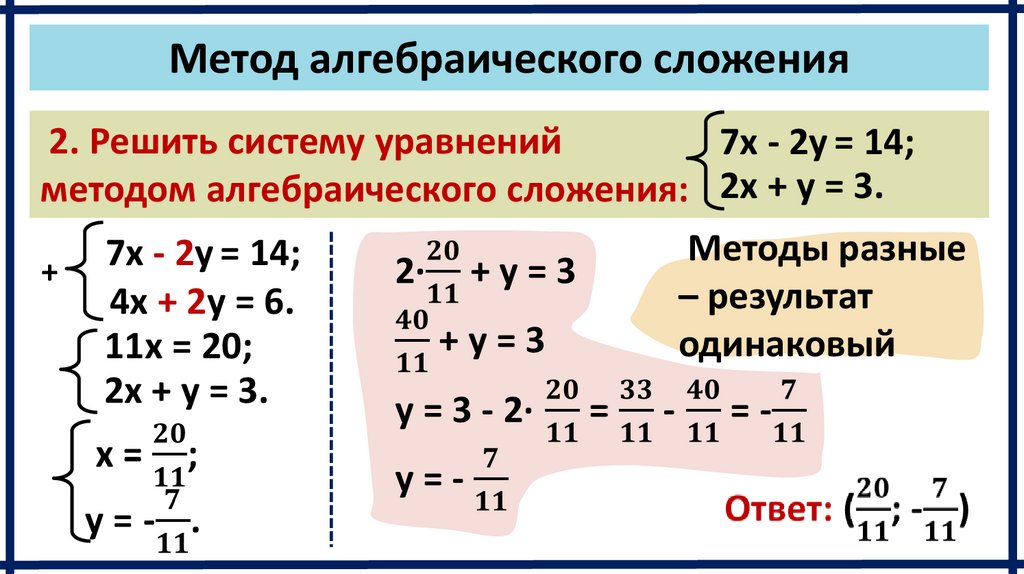
Метод алгебраического сложения
2. Решить систему уравнений
7x - 2y = 14;
методом алгебраического сложения: 2x + y = 3.
Методы разные
7x
2y
=
14;
+
– результат
4x + 2y = 6.
одинаковый
11x = 20;
2x + y = 3.

7.

Какой метод решения рациональнее?
Метод решения хорош, если с самого начала
мы можем предвидеть - и далее подтвердить
это, - что, следуя этому методу, мы достигнем
цели. (Г. Лейбниц)
Выбор метода решения систем уравнений
рационален в зависимости от особенностей
системы уравнений.

8.

Какой метод рациональнее?
Метод
подстановки:
Метод
алгебраического сложения:
Метод сложно применить,
когда из уравнения не
удается в один шаг выразить
одну переменную через
другую. Тогда лучше
выбрать метод сложения.
Метод сложно применить,
когда коэффициенты в
уравнениях выражены
дробными коэффициентами.
Тогда лучше выбрать метод
подстановки.
Например: 5x + 9y = 17
Например: 0,37x + 4,9y = 2

9.

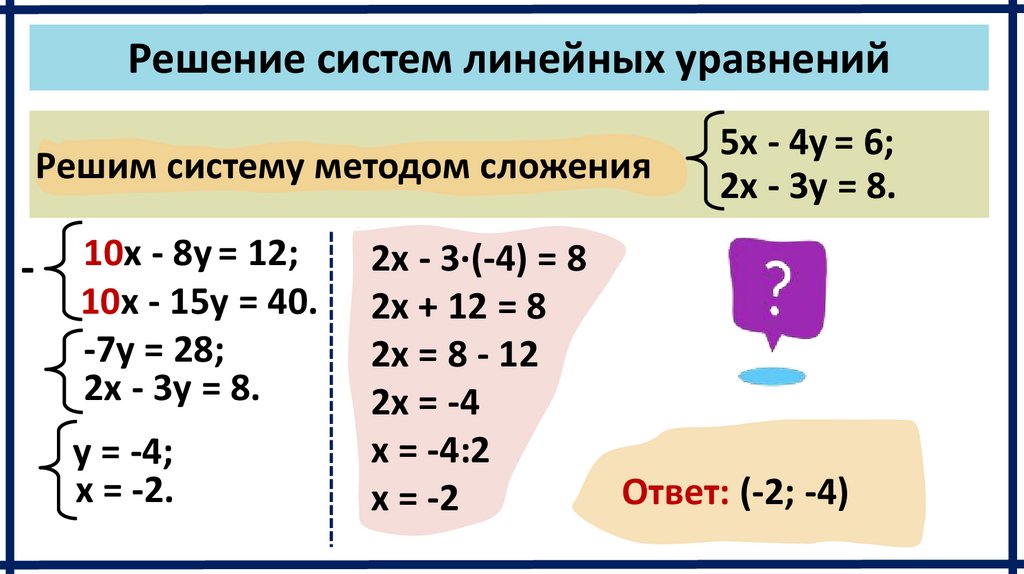
Решение систем линейных уравнений
Решим систему методом сложения
-
10x - 8y = 12;
10x - 15y = 40.
-7y = 28;
2x - 3y = 8.
y = -4;
x = -2.
5x - 4y = 6;
2x - 3y = 8.
2x - 3∙(-4) = 8
2x + 12 = 8
2x = 8 - 12
2x = -4
x = -4:2
Ответ: (-2; -4)
x = -2

10.

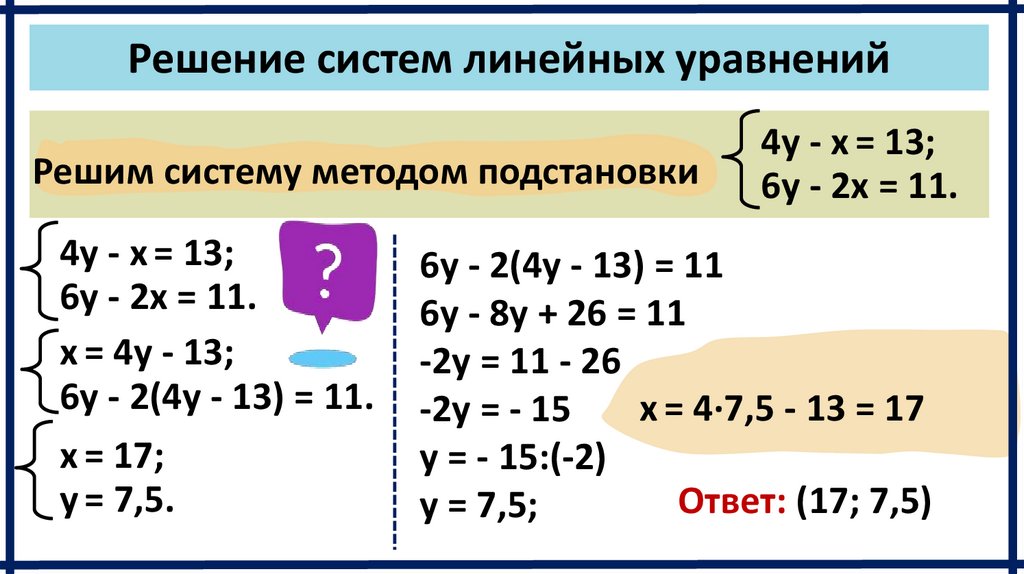
Решение систем линейных уравнений
Решим систему методом подстановки
4y - x = 13;
6y - 2x = 11.
x = 4y - 13;
6y - 2(4y - 13) = 11.
x = 17;
y = 7,5.
4y - x = 13;
6y - 2x = 11.
6y - 2(4y - 13) = 11
6y - 8y + 26 = 11
-2y = 11 - 26
x = 4∙7,5 - 13 = 17
-2y = - 15
y = - 15:(-2)
Ответ: (17; 7,5)
y = 7,5;

11.

Всегда ли система двух линейных уравнений
имеет единственное решение?
Решить систему уравнений:
3y + 2x = 1;
6y + 4x = -3.
Решим систему методом подстановки: Геометрически:
3y + 2x = 1; Уравняем коэффициенты
6y + 4x = -3. при y и вычтем (1) из (2).
6y + 4x = 2; Получим 0 = -5
6y + 4x = -3. Система не имеет решений
Прямые не
имеют точек
пересечения,
они являются
параллельными.

12.

Может ли система двух линейных уравнений
иметь более одного решения?
y + x = 1;
6y + 6x = 6.
Решим систему методом подстановки:
Решить систему уравнений:
y + x = 1;
6y + 6x = 6.
y + x = 1;
y + x = 1.
Уравняем коэффициенты
при y и вычтем (1) из (2).
Геометрически:
Получим 0 = 0
Прямые
Система имеет бесконечное совпадают.
множество решений

13.

Выводы:
Во всех остальных случаях
система имеет единственное
решение.
a1x + b1y + c1 = 0
Система a x + b y + c = 0
2
2
2
Не имеет решений при
условии: a1 = a2; b1 = b2; c1 ≠ c2
a1x + b1y + c1 = 0
Система a x + b y + c = 0
2
2
2
Имеет множество решений при
условии: a1 = a2; b1 = b2; c1 = c2

14.

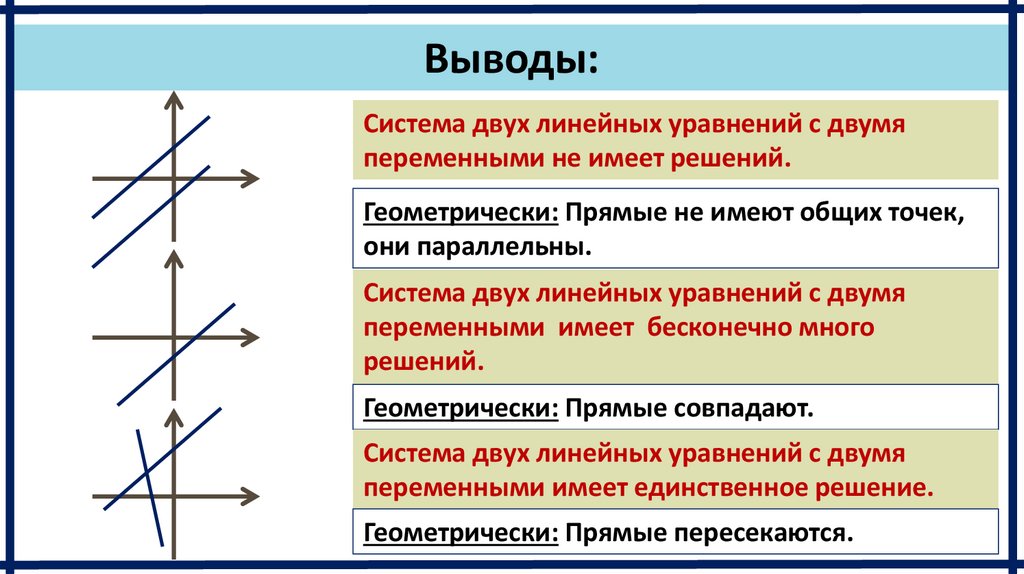
Выводы:
Система двух линейных уравнений с двумя
переменными не имеет решений.
Геометрически: Прямые не имеют общих точек,
они параллельны.
Система двух линейных уравнений с двумя
переменными имеет бесконечно много
решений.
Геометрически: Прямые совпадают.
Система двух линейных уравнений с двумя
переменными имеет единственное решение.
Геометрически: Прямые пересекаются.

15.

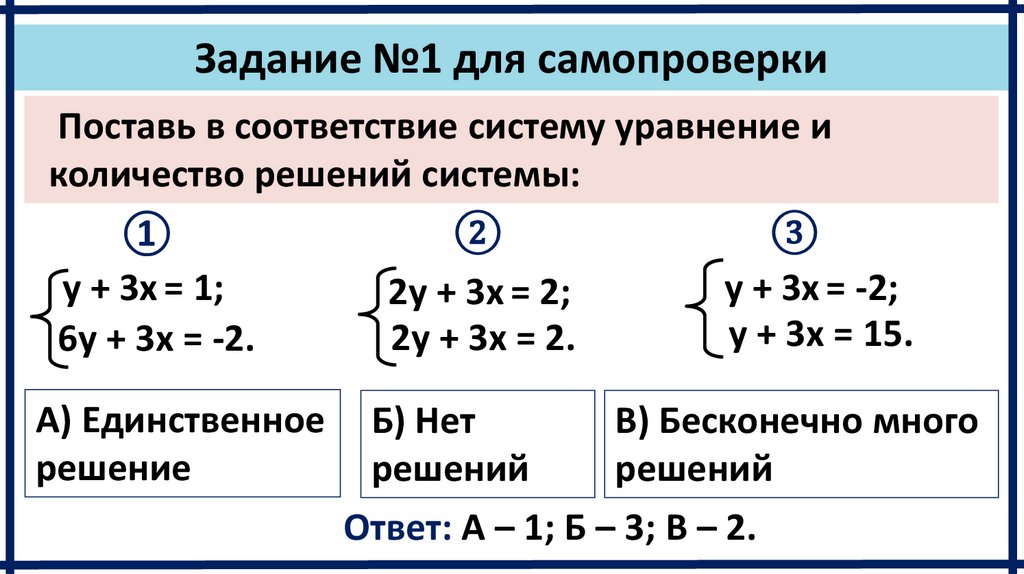
Задание №1 для самопроверки
Поставь в соответствие систему уравнение и
количество решений системы:
②
③
①
y + 3x = 1;
y + 3x = -2;
2y + 3x = 2;
y + 3x = 15.
2y + 3x = 2.
6y + 3x = -2.
А) Единственное
решение
Б) Нет
В) Бесконечно много
решений
решений
Ответ: А – 1; Б – 3; В – 2.

16.

Задание №2 для самопроверки
Поставь в соответствие условия левого и правого
Ответ: 1 – Б; 2 – В; 3 – А.
столбцов:
① Прямые
параллельны
А) Единственное
решение
②
Прямые
совпадают
Б) Нет
решений
③
Прямые
пересекаются
В) Бесконечно
много решений

17.

Задание №3 для самопроверки
Для каких систем пара чисел (-2; 2) является
решением?
①
③
3y + 4x = 2;
2y + 7x = 10.
②
5y + 2x = -6;
6y + 5x = -2.
y + 3x = -2;
8y + 3x = 15.
Ответ: 1,2.