01eb8d6ea55f4b0c979c67da45ab9c96

1. Построение графика квадратичной функции

2. Актуализация знаний

• Выбрать из приведенного списка уравнений
функций только те, которые относятся к
квадратичным.

3.

Актуализация знаний
• Выбрать из приведенного списка
уравнений функций только те, которые
относятся к квадратичным.

4.

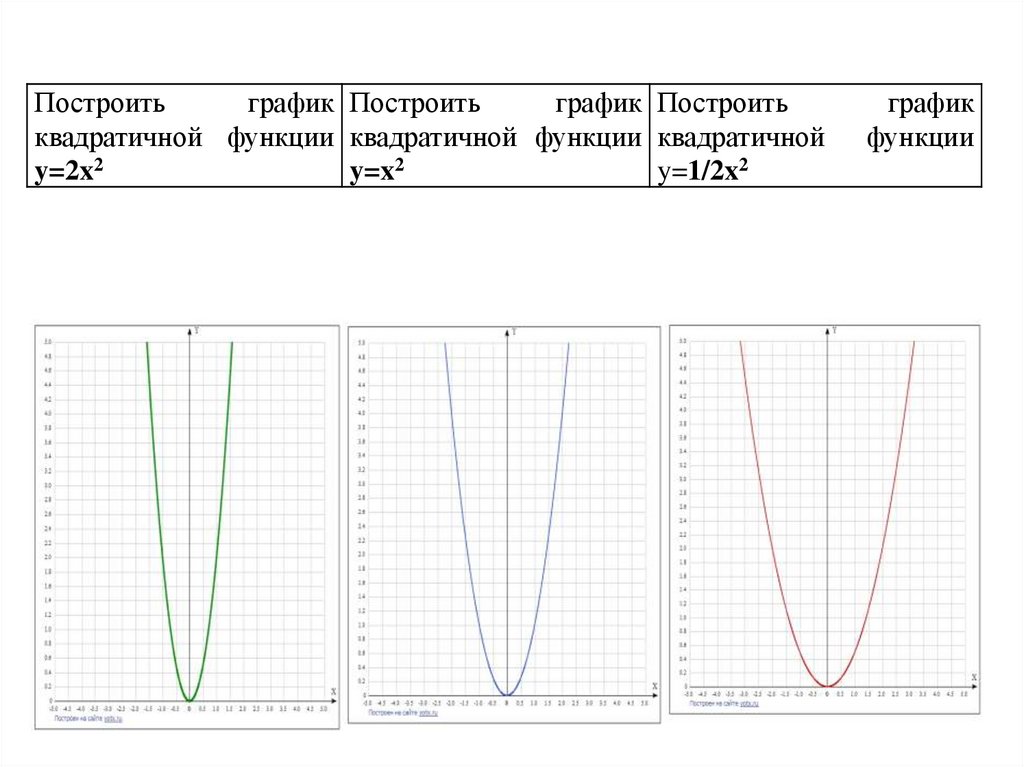
Построить
график Построить
график Построить
квадратичной функции квадратичной функции квадратичной
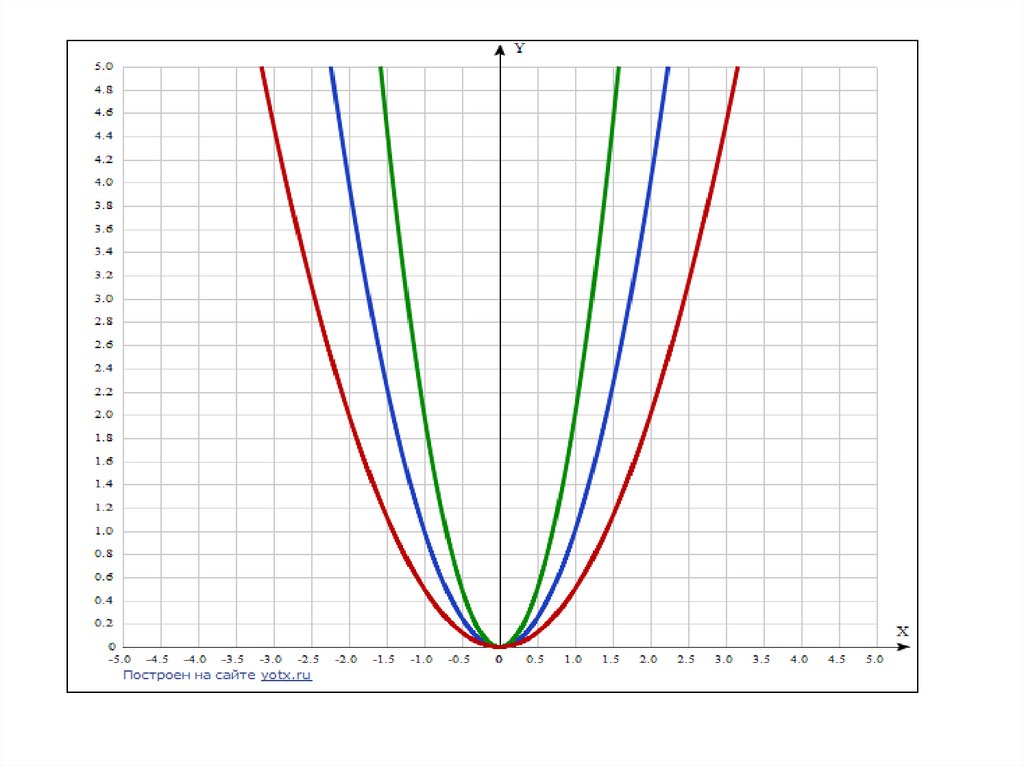
y=2x2
y=x2
y=1/2x2
график
функции

5.

6.

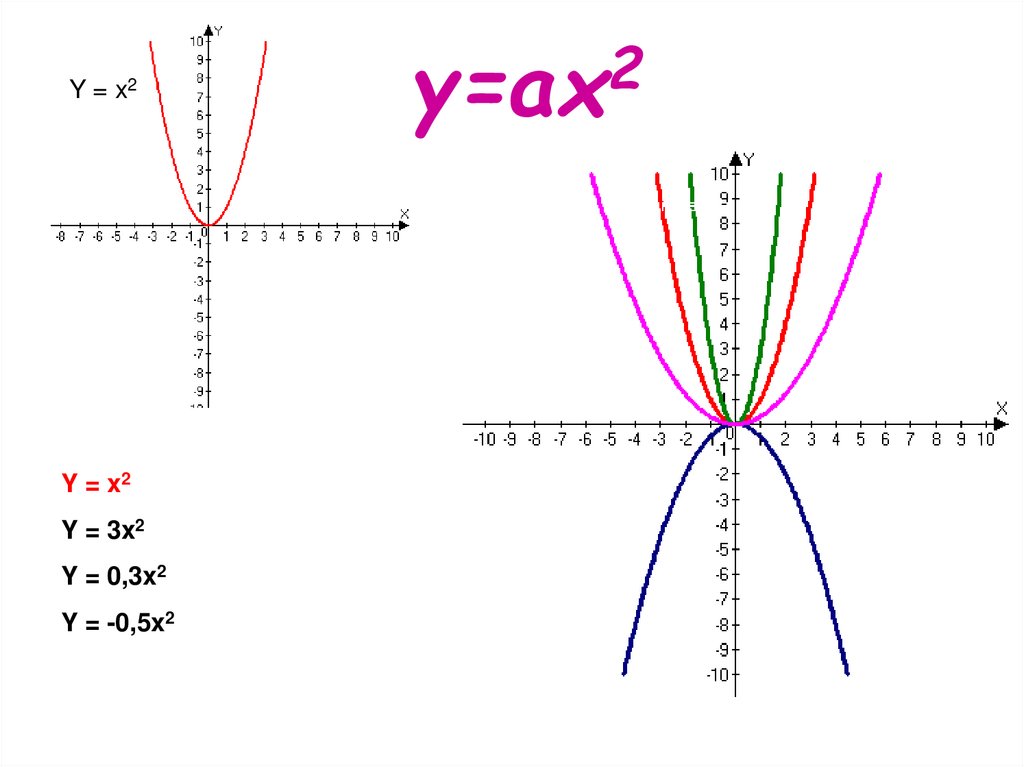
Y = x2
Y = x2
Y = 3x2
Y = 0,3x2
Y = -0,5x2
2
y=ax

7.

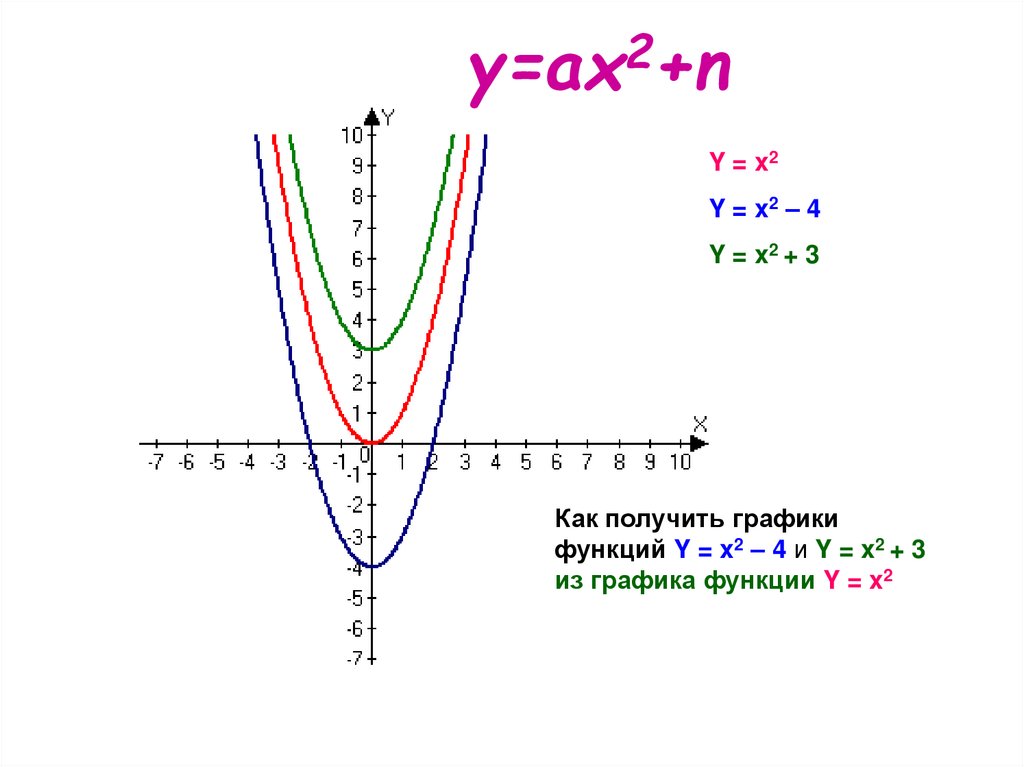
y=ax2+n
Y = x2
Y = x2 – 4
Y = x2 + 3
Как получить графики
функций Y = x2 – 4 и Y = x2 + 3
из графика функции Y = x2

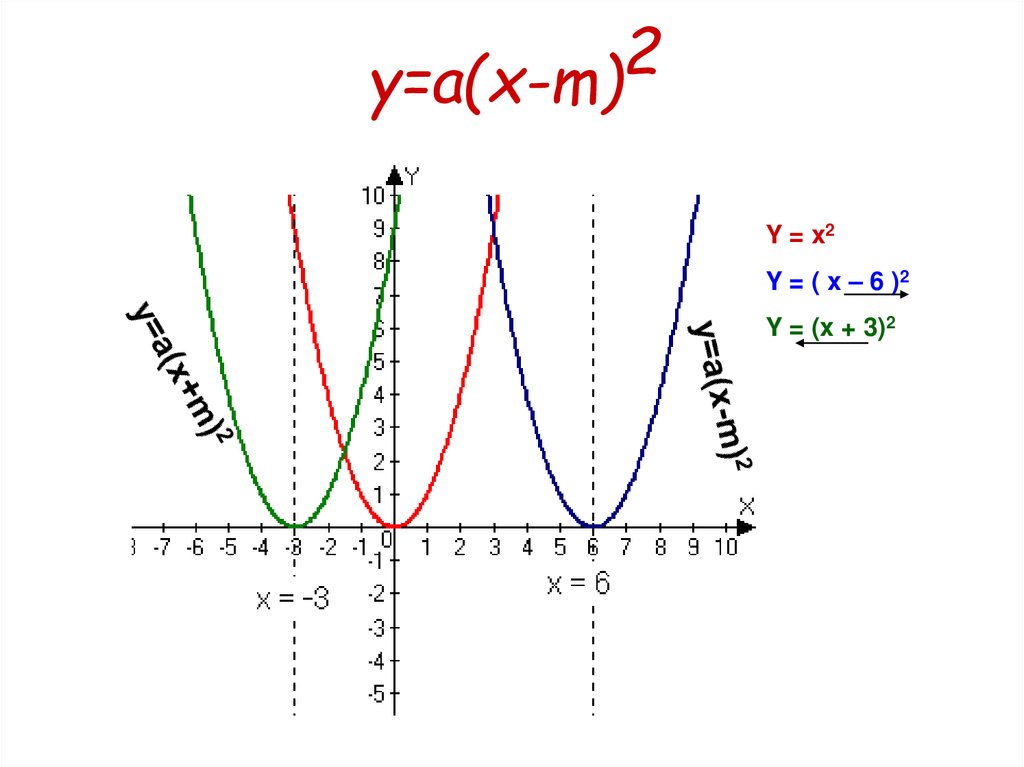
8. y=a(x-m)2

2
y=a(x-m)
Y = x2
Y = ( x – 6 )2
Y = (x + 3)2

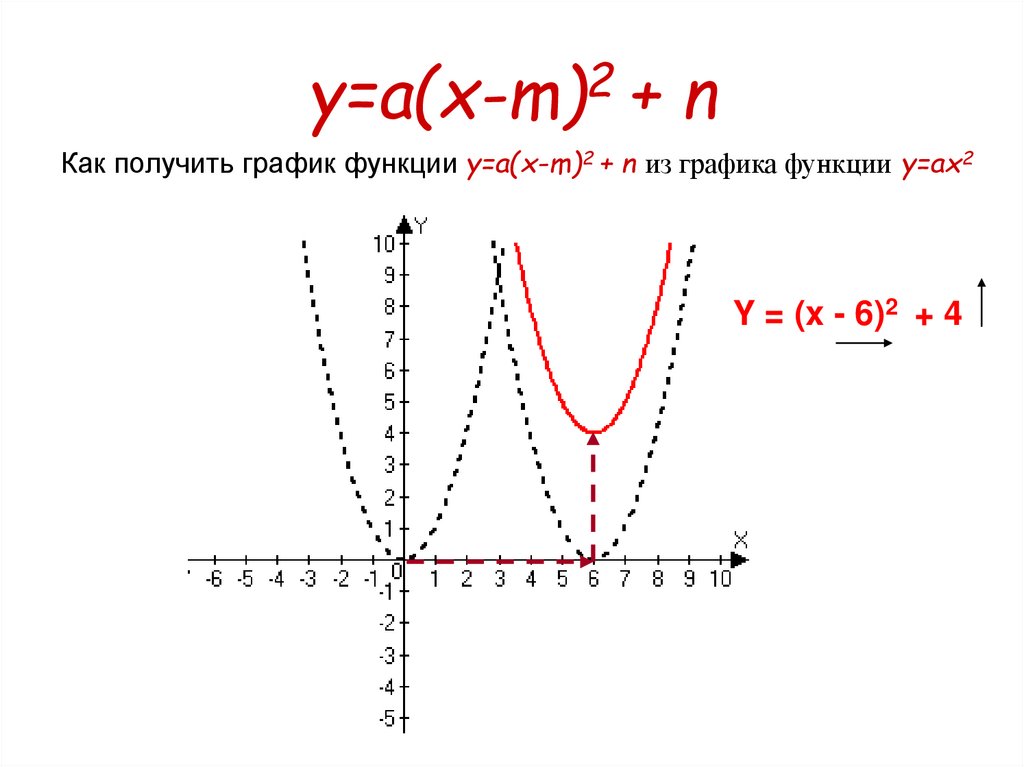
9. y=a(x-m)2 + n

Как получить график функции y=a(x-m)2 + n из графика функции y=ax2
Y = (x - 6)2 + 4

10.

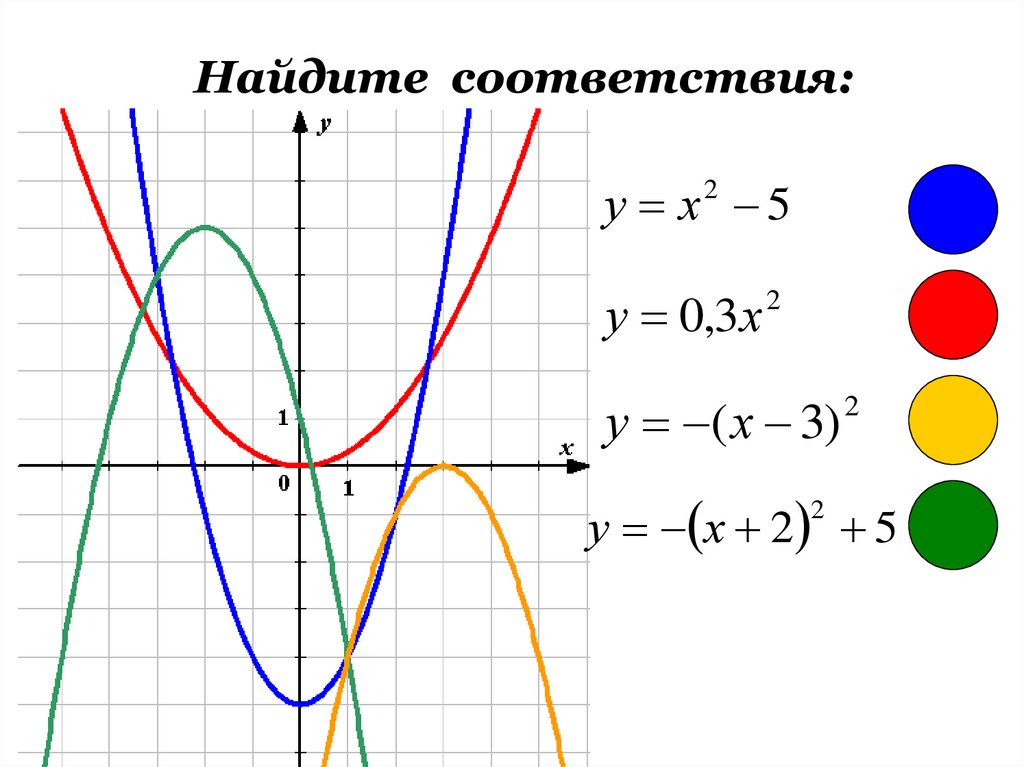
Найдите соответствия:
у х2 5
у 0,3х
2
у ( х 3) 2
у х 2 5
2

11.

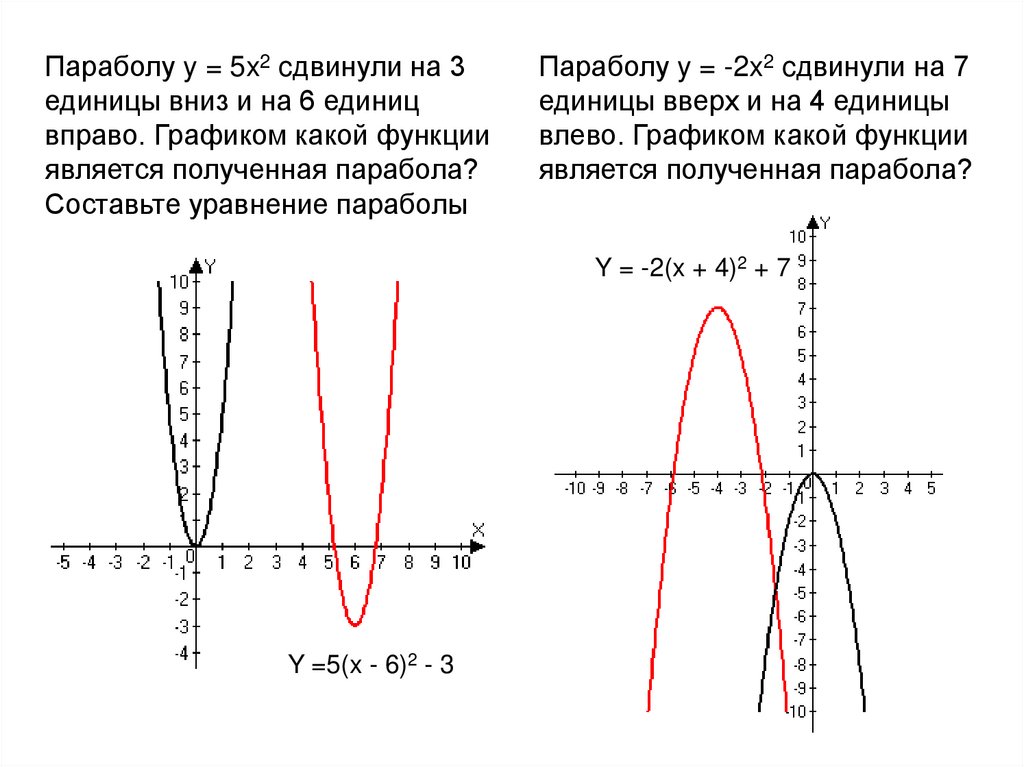
Параболу y = 5x2 cдвинули на 3
единицы вниз и на 6 единиц
вправо. Графиком какой функции
является полученная парабола?
Составьте уравнение параболы
Параболу y = -2x2 cдвинули на 7
единицы вверх и на 4 единицы
влево. Графиком какой функции
является полученная парабола?
Y = -2(x + 4)2 + 7
Y =5(x - 6)2 - 3

12. Построение графика функции у = ах2 + bх +с.

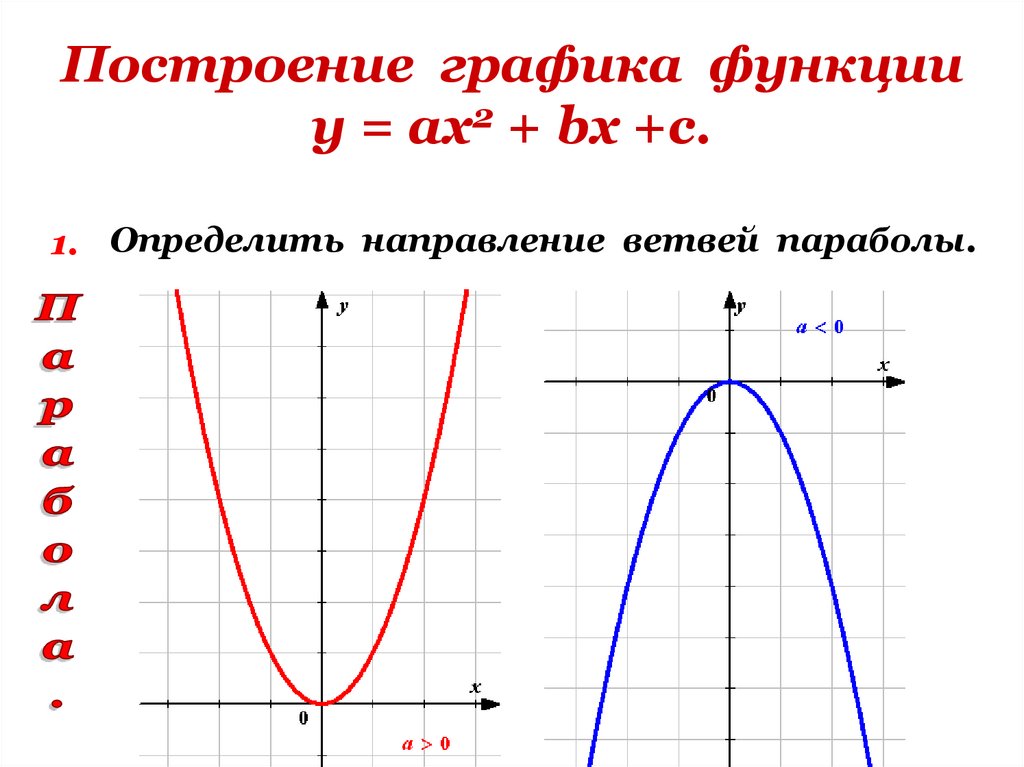
1. Определить направление ветвей параболы.

13. Построение графика функции у = ах2 + bх +с.

х т
Построение графика функции
у = ах2 + bх +с.
2. Найти координаты вершины параболы
(т; п).
b
т
2a
n y m
3. Провести ось
симметрии.
х т
О (т;п)

14. Построение графика функции у = ах2 + bх +с.

Определить точки пересечения графика
4. функции с осью Ох, т.е. найти нули
функции.
у 0
ах bx c 0
2
(х1;0)
(х2;0)

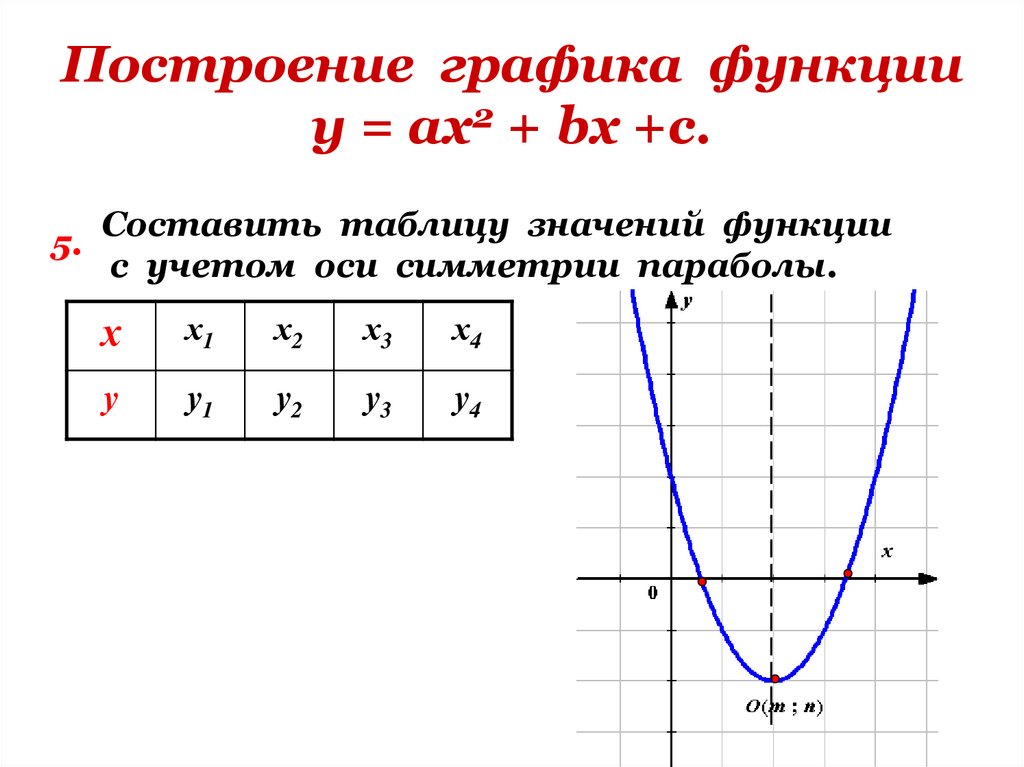
15. Построение графика функции у = ах2 + bх +с.

5.
Составить таблицу значений функции
с учетом оси симметрии параболы.
х
х1
х2
х3
х4
у
у1
у2
у3
у4

16. Алгоритм построения графика функции у = ах2 + bх +с.

1. Определить направление ветвей параболы.
2. Найти координаты вершины параболы
(xв; yв).
3. Провести ось симметрии.
4. Определить точки пересечения графика
функции с осью Ох, т.е. найти нули
функции.
5. Составить таблицу значений функции
с учетом оси симметрии параболы.

17. Первый шаг 1.Определить направление ветвей параболы:

у = х2 – 6х +8
а=1,
а > 0.
Значит ветви параболы направлены вверх
17

18. Второй и третий шаги

Найдем координаты
вершины параболы
у =х2 – 6х +8
m= - b/2а = 6/2 = 3
n= 32 – 6 • 3 + 8= - 1.
Вершина параболы имеет
х
координаты
(3; -1).
Отметим её в
координатной
плоскости.
Проведём ось симметрии
параболы.
у
2
1
0
1
2
3
4
-1
18

19. Четвёртый шаг

Найдем точки пересечения
графика функции с осью х ,
тогда у=0.
х2 - 6х +8=0
Решим квадратное уравнение.
D = b2 – 4ас= 36 - 4 •1• 8= 4, D > 0 ,
два корня
Х₁=4, Х₂ = 2.
(4; 0) (2;0)
Найдем точку пересечения с
осью у , тогда х=0
0 2 - 6 •0 +8 = 8
(0; 8)
Отметим и эти точки в
координатной плоскости.
у
8
7
6
5
4
3
2
1
1
2
3
4
х
-1
19

20. Пятый шаг

Составим таблицу значений
х
у
2
0
4
0
1
3
5
3
0
8
у = х2 – 6х +8
6
8

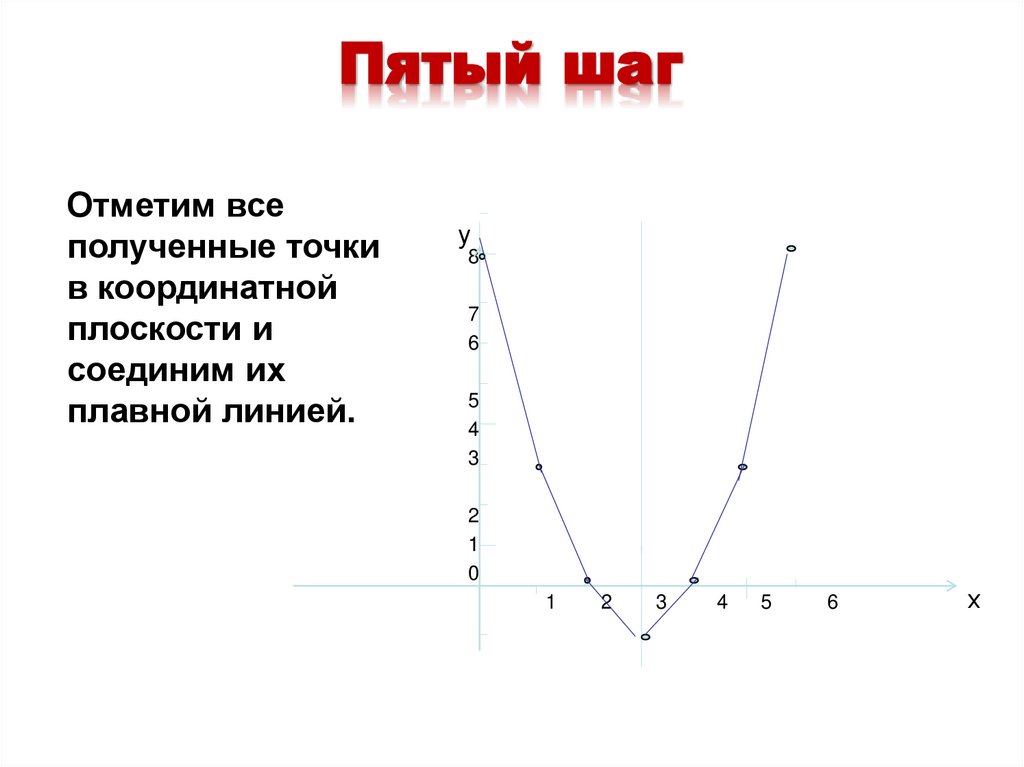
21. Пятый шаг

Отметим все
полученные точки
в координатной
плоскости и
соединим их
плавной линией.
у
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
х

22.

ДОМАШНЕЕ ЗАДАНИЕ
Постройте график функции y = x2 – 2x - 3.
С помощью графика найдите:
1. Область определения функции;
2. Область значений функции;
3. Нули функции;
4. Промежутки, в которых у>0, y<0;
5. Промежутки возрастания и убывания функции;
6. Наибольшее (наименьшее) значение функции

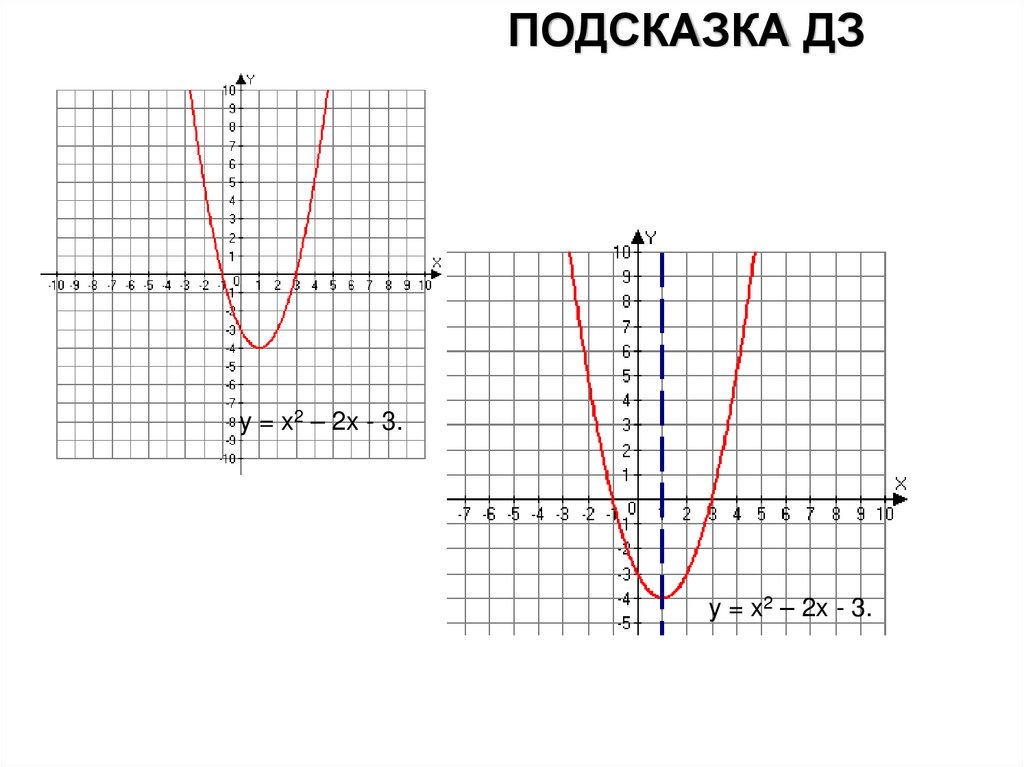
23.

ПОДСКАЗКА ДЗ
y = x2 – 2x - 3.
y = x2 – 2x - 3.