!Вероятности_случ_событий_Сложение_вероятностей_

1. Вероятность случайного события. Вероятности событий в опытах с равновозможными элементарными событиями

2.

Повторение. Какие элементарные события
называются равновозможными?
Приведите примеры равновозможных элементарных событий
Чему равна вероятность каждого элементарного события, если
случайный опыт содержит N равновозможных элементарных событий?
Правило: В опыте с равновозможными элементарными событиями
вероятность события А равна отношению числа элементарных
событий, благоприятствующих событию А, к общему числу
элементарных событий.
Док-во: Обозначим N (A) - число элементарных
событий, благоприятствующих
событию A. Вероятность события А равна сумме
вероятностей благоприятствующих ему элементарных
событий:
1 1
1 N ( A)
P( A) ...
N N
N
N

3. Примеры:

1. При трёхкратном бросании монеты нас интересует событие
A={выпал ровно один орёл}.
Какова вероятность этого события?
2. На каждые 1200 качественных пакетов молока в среднем приходится
50, которые протекают. Какова вероятность того, что случайно
выбранный пакет молока не течёт?
3. В чемпионате по гимнастике участвуют 76 спортсменок: 30 из
России, 27 из Казахстана, остальные — из Белоруссии. Порядок, в
котором выступают гимнастки, определяется жребием. Найдите
вероятность того, что спортсменка, выступающая третьей, окажется из
Белоруссии.
4. Для составления графика дежурств класс разбили на 7 групп по 3
человека в каждой. Найдите вероятность того, что учащиеся в этом
классе Таня и Даня попадут в одну группу.

4. Решите задачи самостоятельно(15 минут):

1. Научная конференция проводится 3 дня. Всего запланировано 50 докладов:
в первый день – 30 докладов, а остальные распределены поровну между
вторым и третьим днями. Порядок докладов определяется жеребьевкой.
Какова вероятность, что доклад профессора М. окажется запланированным на
последний день конференции?
2. Перед началом первого тура чемпионата по теннису разбивают на игровые пары
случайным образом с помощью жребия. Всего в чемпионате участвует 46
теннисистов, среди которых 19 участников из России, в том числе Ярослав Исаков.
Найдите вероятность того, что в первом туре Ярослав Исаков будет играть с каким –
либо теннисистом из России.
3. Пользуясь принципом равновозможности, найдите вероятность одного элементарного
исхода в опыте, в котором монету бросают: а) 3 раза; б) 5 раз; в) 8 раз; г) 10 раз; д) n раз.
4. Пользуясь принципом равновозможности, найдите вероятность одного
элементарного исхода в опыте, в котором игральную кость бросают:
а) дважды; б) трижды; в) четыре раза.
5. Правильную монету бросили 10 раз. Какова вероятность того,
что в результате выпадет
а) ровно один орёл? Б) 10 орлов? В) 9 орлов?

5.

Повторение
Что называется суммой (объединением) событий А и В?
Суммой нескольких событий называется событие,
состоящее в наступлении хотя бы одного из них в
результате испытания.
Пример: в ящике находится красный, черный и белый шары.
А- извлечение черного шара
В- извлечение красного шара
С- извлечение белого шара
А+В – извлечен черный или красный шар
В+С – извлечен красный или белый шар
А+С – извлечен черный или белый шар

6. Теорема сложения вероятностей

Вероятность появления одного из двух несовместных
событий, равна сумме вероятностей этих событий:
Р(А+В)=Р(А)+Р(В)
Вероятность появления одного из нескольких попарно
несовместных событий равна сумме вероятностей этих
событий: Р( А1 А2 А3 ... Аn) Р( А1) Р( А2) Р( А3) ... Р( Аn)
Р( i 1 Аi) i 1 Р( Аi)
n
n
Сумма вероятностей попарно несовместных событий,
образующих полную группу А1, А2, А3, ..., Аn, равна 1.
Сумма вероятностей противоположных событий равна 1
___
Р( А) Р( А ) 1

7.

Повторение
Что называется произведением (пересечением) событий А и В?
Произведением событий А и В называют
событие, которое наступает тогда и
только тогда, когда наступает и событие
А и событие В.
Оно обозначается А·В или АВ.

8.

Пример1.
Дать описание произведения АВ
событий А и В, если
а) А=«цена товара больше 100 руб.»;
В =«цена товара не больше 110руб.»;
100< S≤110 (S-цена товара)
б)А=«завтра пятница»,
В=«завтра 13–е число»;
А*В =« Завтра пятница 13-ое»

9.

в)А- координаты случайно выбранной точки на
плоскости удовлетворяют неравенству x²+y²≤1;
В- координаты случайно выбранной точки
положительны;
·
(x;y)

10.

г) А- случайно выбранное двузначное
число четно;
В- случайно выбранное число делится
на 11.
А*В = {22, 44, 66, 88}

11.

Пример

12.

Задачи:
1. При выполнении контрольного задания учащийся может получить одну из
четырёх отметок. Вероятность получить «неудовлетворительно» равна 0,1,
вероятность получить «удовлетворительно» –– 0,2, вероятность получить
«хорошо» –– 0,3, четвёртая возможная отметка –– «отлично».
Какова вероятность того, что учащийся получит хорошую или отличную отметку?
Ответ: р= 0,3+0,4 = 0,7 или р= 1-(0,1+0,2)=0,7
2. В течение года с автомобилем может произойти одно из трёх событий: он
не попадёт в аварию, он попадёт в мелкую аварию, он попадёт в серьёзную
аварию. Для неопытного водителя в некотором регионе вероятность попадания в
мелкую аварию равна 0,1, а вероятность попадания в серьёзную аварию в пять
раз меньше. Какова вероятность того, что неопытный водитель не попадёт в
аварию в течение года?
Ответ: 1- (0,1+0,1/5) = 1-(0,1+0,02) = 0,88
3. Для социологического опроса некоторой совокупности людей была составлена
случайная выборка из 2000 человек. На вопрос «Нравились ли вам уроки
математики в школе?» утвердительно ответило 1178 из них. Пользуясь этими
данными, оцените вероятность (найдите приближённое значение вероятности)
того, что случайно выбранный из этой совокупности человек утвердительно
ответит на тот же вопрос.
Ответ: р=0,589

13.

4. В двух книжных магазинах был проведён опрос двух случайных выборок
покупателей. В первой выборке было 1520 человек, во второй выборке было
580 человек.
В первой выборке 623 покупателя утвердительно ответили на вопрос
«Читали ли вы хотя бы одно произведение писателя П?».
Во второй выборке на этот же вопрос утвердительно ответили 217 человек.
Оцените вероятность того, что случайно выбранный покупатель в книжном
магазине утвердительно ответит на этот же вопрос, пользуясь:
а) результатами опроса только первой выборки;
б) результатами опроса только второй выборки;
в) результатами, полученными с использованием объединённой выборки.
По вашему мнению, на какое из полученных чисел лучше полагаться при
оценке вероятности указанного события?
А) р=623/1520=0,41
Б) р=217/580=0,37
В) р=(623+217)/(1520+580) = 0,4

14. Близость частоты и вероятности

Пример. В классе провели опрос «У кого в семье живет собака?».
Опрос показал, что из 32 учеников собаку дома имеют 7.
Значит, неизвестная вероятность события «В случайно выбранной семье
есть собака» оценивается дробью 7/32.
Можно ли утверждать, что эта оценка — точное значение вероятности события «У школьника дома есть собака»?
Такая оценка — случайная величина. Она зависит от выборки и будет
меняться от класса к классу

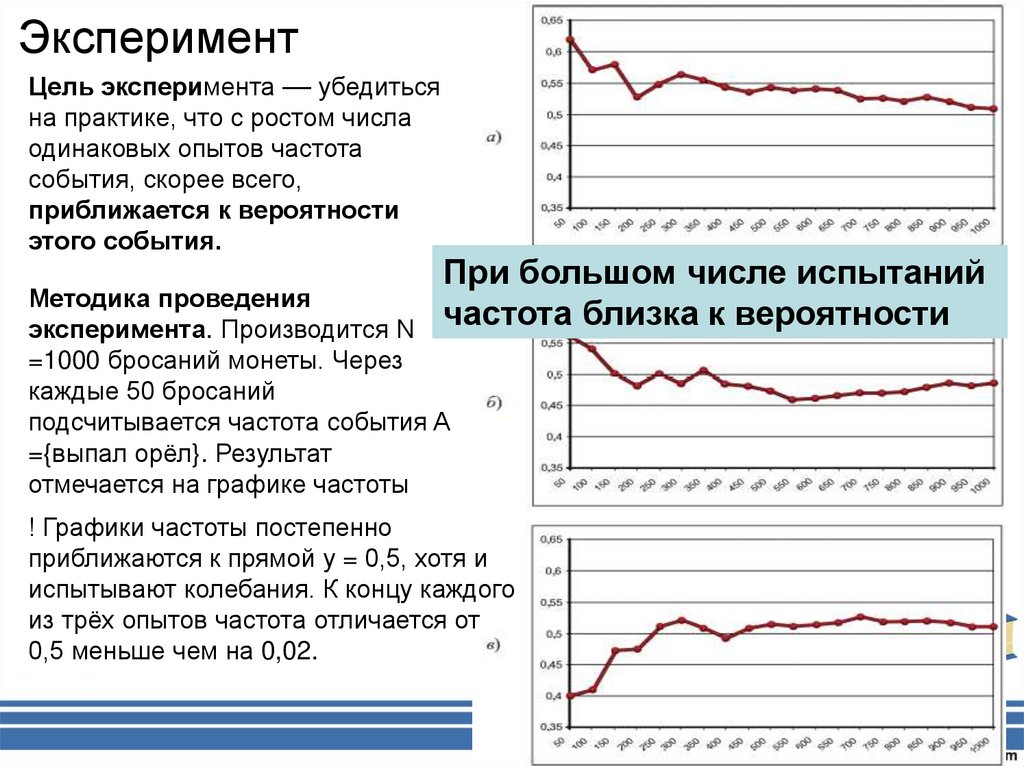
15. Эксперимент

Цель эксперимента –– убедиться
на практике, что с ростом числа
одинаковых опытов частота
события, скорее всего,
приближается к вероятности
этого события.
При большом числе испытаний
частота близка к вероятности
Методика проведения
эксперимента. Производится N
=1000 бросаний монеты. Через
каждые 50 бросаний
подсчитывается частота события A
={выпал орёл}. Результат
отмечается на графике частоты
! Графики частоты постепенно
приближаются к прямой y = 0,5, хотя и
испытывают колебания. К концу каждого
из трёх опытов частота отличается от
0,5 меньше чем на 0,02.

16.

Решите задачи:
1. Найдите вероятность того, что при одном бросании
игрального кубика выпадет
А) число очков больше четырёх;
Б) число очков, не кратное трем
2. Найдите вероятность того, что при двукратном
бросании игрального кубика сумма очков:
А) равна 1
Б) меньше 13
В) меньше 5
Г) меньше 10

17.

Решите задачи:
3. Ученику предложили написать любое двузначное
число. Найдите вероятность того, что число:
А) не оканчивается нулем;
Б) состоит из различных цифр;
В) не является квадратом целого числа
Г) не делится на 17
4. Два ученика независимо друг от друга написали на
доске по одному двузначному числу. Найдите
вероятность того, что:
А) эти числа различные;
Б) сумма чисел равна 100;
В) сумма чисел не больше 25;
Г) сумма чисел больше 190

18. Теорема сложения вероятностей совместных событий

Вероятность появления хотя бы одного из двух
совместных событий равна сумме вероятностей этих
событий без вероятности их совместного
наступления(произведения):
Р( А В) Р( А) Р( В) Р( АВ)

19.

Пример 1
Проверьте с помощью таблицы и классической
формулы вероятности

20.

Пример 2
Проверьте с помощью таблицы и классической
формулы вероятности

21. Обобщение формулы сложения на случай трёх событий

Для любых трёх событий A, B и C формула сложения вероятностей
принимает вид
P(A ∪B ∪C) = P(A)+P(B)+P(C)−P(A ∩B)−P(A ∩C)−P(B ∩C)+P(A ∩B ∩C).
Суть формулы: чтобы найти вероятность объединения трёх событий, нужно
сложить их вероятности, вычесть вероятности попарных пересечений и
добавить вероятность пересечения всех трёх событий.

22.

Вероятность произведения независимых событий

23.

Пример:

24.

25.

ДОМАШНЕЕ ЗАДАНИЕ:
Дан круг радиуса 3 с центром в т. 0,0 .
В круге отмечают все точки, абсциссы и ординаты
которых являются целыми числами.
Из отмеченных точек случайным образом выбирают
одну.
Найти вероятность того, что она:
А)лежит на оси абсцисс;
Б) лежит не на координатных осях;
В) принадлежит кругу с центром в (0,0) радиуса 1;
Г) ее абсцисса и ордината отличаются более чем на 2

26. Условная вероятность

27.

Задача. 1. На столе лежат 4 синих и 3 красных карандаша.
Ученик дважды наугад берет по одному карандашу и обратно
их не кладет. Найти вероятность того, что вторым был взят
красный карандаш при условии, что первым был синий
События:
А- вторым был взят красный карандаш
В- первым вынут синий карандаш
Обозначение: А | В (произошло событие А при условии, что произошло событие В)
Р (А | В) – условная вероятность события А при условии В

28. Задачи 1. 2 - 4. На столе лежат 4 синих и 3 красных карандаша. Редактор дважды наугад берет по одному карандашу и обратно их не

кладет.
2. Найти вероятность того, что вторым был СИНИЙ при условии,
что первым был СИНИЙ
3. Найти вероятность того, что вторым был СИНИЙ при условии,
что первым был КРАСНЫЙ
4. Найти вероятность того, что вторым был КРАСНЫЙ при
условии, что первым был КРАСНЫЙ

29.

Задача 2. В барабане находится 10 лотерейных билетов, из них 2 выигрышных.
Из барабана 2 раза вынимают по одному билету, не возвращая их обратно.
Какова вероятность того, что: в первый раз был вынут выигрышный билет, а во
второй раз - билет без выигрыша.
Событие А - первым вынут выигрышный билет
В - второй вынут билет без выигрыша
1. Вероятность того, что сначала вынут выигрышный билет P(А)= ?
2. Вероятность того, что вторым вынут билет без выигрыша (произошло событие
В) вычисляется при условии, что первым уже вынули выигрышный билет:
Р(В|А)=(10 – 2 ) / (10 – 1) = 8 / 9
3. P (A*B) = P(А) * Р(В|А) = ?
Ответ:

30.

ЗАДАЧА 3. В конце экзамена два оставшихся студента по очереди
вытягивают по одному билету. Первым будет тянуть Иванов, а
вторым –– Петров. На столе осталось три билета: восьмой,
пятнадцатый и девятнадцатый.
Вычислить вероятность события «Иванов взял билет № 8,
а Петров –– № 19».
События: А = «Иванов взял билет № 8», В = «Петров взял билет
№ 19».
1. Р(А) = ?
2. Р (В|A) = ?
3. Р(А*В) = Р(А) * Р (В|A) =
Ответ:

31. Задача 4.

В магазине в продаже осталось 5 телефонов одной марки, со скидкой:
– Два черных
– 1 серебристый
– 1 красный
– 1 голубой
В магазин зашли 2 покупателя, каждый с целью приобретения телефона.
Какова вероятность того, что будут проданы два черных телефона?
Задача 5.

32. Задача 6

Задача 7

33. Задача 8

Среди 100 выпускников 11 класса лицея 75 имеют рост меньше 1 м
80 см и 25 – рост, больший или равный 1 м 80 см. Найдите
вероятность того, что среди трех случайно встреченных
выпускников двое окажутся ниже, а один выше 1 м 80 см.
Задача 9
Вероятность того, что два брата – Ваня и Петя – моют руки перед
обедом, равна, 0,32.
Известно, что Ваня моет руки перед обедом с вероятностью 0,8. С
какой вероятностью Петя моет руки перед едой?

34. Разные задачи. Решите самостоятельно

1. В классе 26 человек, среди них два близнеца — Андрей и Сергей.
Класс случайным образом делят на две группы по 13 человек в
каждой. Найдите вероятность того, что Андрей и Сергей окажутся
в одной группе.
2. Игральную кость бросают дважды. Найти вероятность того, что
разность числа очков на первой и второй кости будет от 2 до 5
(включительно).
3. Бросают 2 игральные кости. Найти вероятность того, что на
первой кости выпало не более 4 очков, при условии, что сумма
очков четная.

35.

4.
Игральную кость бросили два раза. Известно, что 6 очков не
выпало ни разу. Найдите при этом условии вероятность
события «сумма очков равна 8».
5.

36. Задачи дополнительные:

1. В некотором банке два круглосуточных банкомата. Каждый из них
исправно работает ночью с вероятностью 0,8. Вероятность того, что
исправно работают оба, равна 0,64.
Найти вероятность того, что нам удастся снять наличные в этом
отделении банка (то есть что хотя бы один из банкоматов исправен).