Лекция 1_Отношения на множестве (1)

1. Отношения на множестве

Лекция 1

2.

В математике изучают не только связи
между элементами двух множеств, но и
связи между элементами одного
множества.
Такие связи называют отношениями на
множестве.

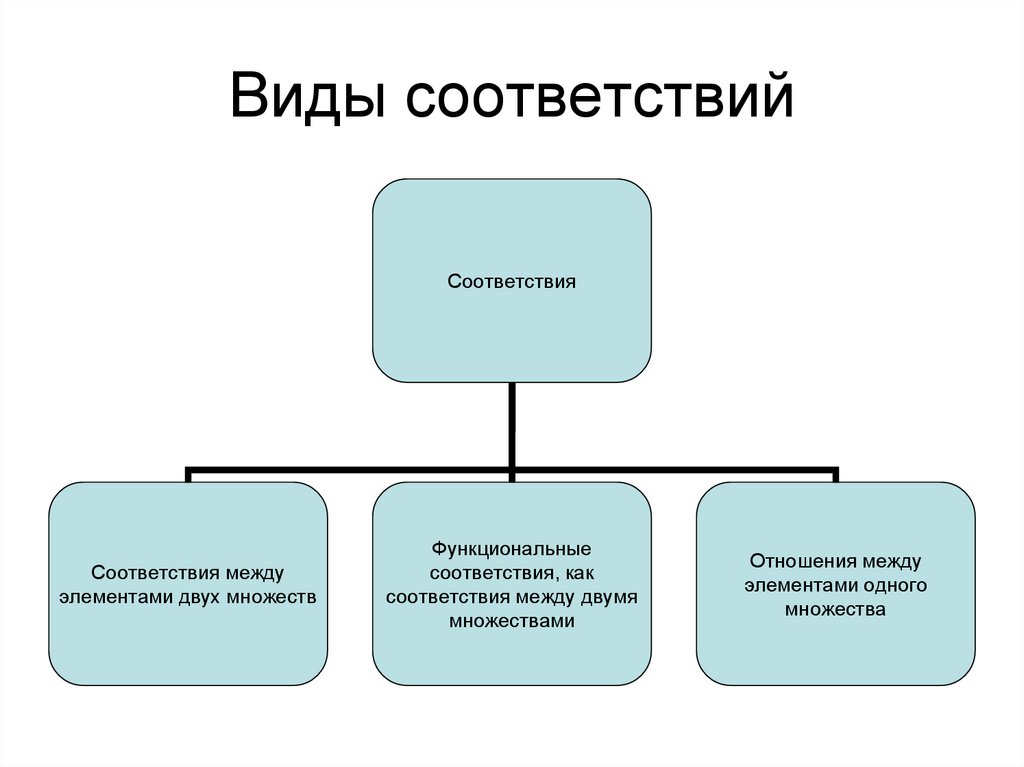
3. Виды соответствий

Соответствия
Соответствия между
элементами двух множеств
Функциональные
соответствия, как
соответствия между двумя
множествами
Отношения между
элементами одного
множества

4. Понятие отношения на множестве

• Определение:
• Бинарным отношением на множестве X
называется всякое подмножество
декартова произведения X×X.
• Символическая запись «xRy» читается :
элемент x находится в данном
отношении R с элементом y.

5.

• Отношения на множестве обозначают
также, как и соответствия: буквами
R,S,T,P и др.
• Если R – отношение на множестве X, то
согласно определению R X X
И наоборот, если задано некоторое подмножество X X
то оно определяет на множестве X некоторое отношение R.

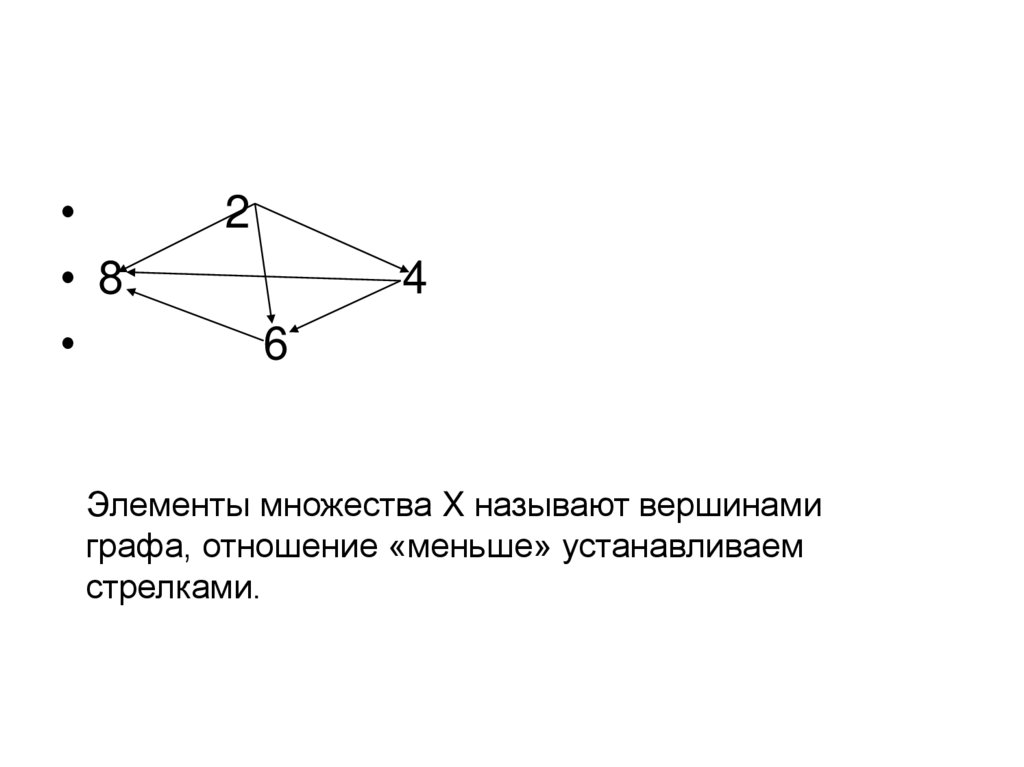
6. Например:

• На множестве X={2,4,6,8} задано
отношение R- быть меньше.
• Построим граф этого отношения

7.

• 8
2
4
6
Элементы множества X называют вершинами
графа, отношение «меньше» устанавливаем
стрелками.

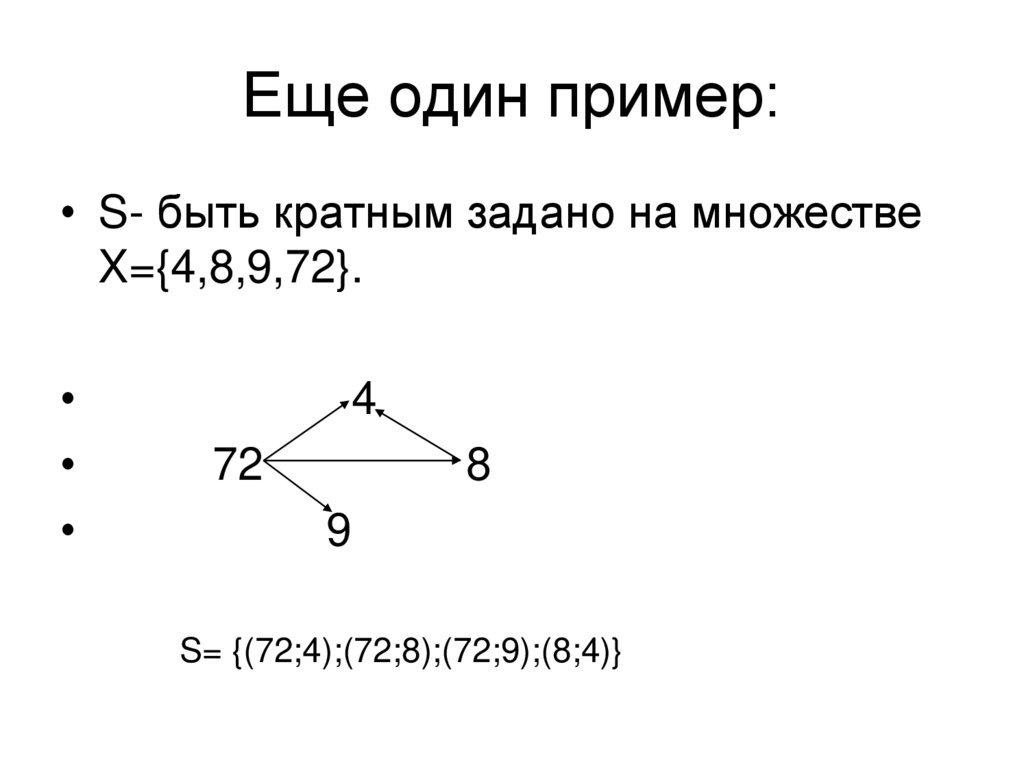
8. Еще один пример:

• S- быть кратным задано на множестве
X={4,8,9,72}.
4
72
8
9
S= {(72;4);(72;8);(72;9);(8;4)}

9. Способы задания отношений

• 1 . Перечисление пар;
• 2. Иллюстрация с помощью графа
(построение графа);
• 3. Словесная формулировка
отношения.

10. Свойства отношений

• 1. Свойство рефлексивности.
• 2. Свойство симметричности.
• 3. Свойство транзитивности.
• 4. Свойство связанности.

11. 1. Свойство рефлексивности.

• Определение: Отношение R на
множестве X называется
рефлексивным, если о каждом
элементе множества X можно сказать,
что он находиться в отношении R с
самим собой.
• R рефлексивно на X
x X
x R x для любого

12. Примеры рефлексивных отношений

• - Быть кратным;
• - Быть равным;
• - Быть параллельным, на множестве
прямых плоскости;
• - Быть подобным на множестве
треугольников;
• - Быть коллинеарным на множестве
векторов.

13.

• Отношение антирефлексивно, если
элемент множества X не находится в
данном отношении с самим собой.
• Например:
• - быть больше на множестве
натуральных чисел;
• - быть перпендикулярным на множестве
прямых.

14. 2. Отношение симметричности.

• Определение: отношение R на
множестве X называется отношением
симметричности, если выполняется
условие: из того, что элемент х
находится в отношении R с элементом
y, следует, что и элемент y находится в
отношении R с элементом х.

15. Символическая запись определения:

• R симметрично на X

16. Примеры симметричных отношений

• - Быть равным;
• - Быть параллельным, на множестве
прямых плоскости;
• - Быть подобным на множестве
треугольников;
• - Быть коллинеарным на множестве
векторов.
• - Быть перпендикулярным на
множестве прямых

17. Свойство антисимметричности

• Определение: Отношение R на множестве X
называется антисимметричным, если для
различных элементов x и y из множества X
выполнено условие: из того, что x находится
в отношении R с элементом y, следует, что
элемент y в отношении R с элементом x НЕ
находится.
• R антисимметрично на X
xRy x y yRx

18. Примеры антисимметричных отношений.

• - быть больше;
• - быть больше на 2
• - быть длиннее
• -быть кратным
• -быть делителем

19. 3. Свойство транзитивности

• Определение: отношение R на
множестве X называется транзитивным,
если выполняется условие: из того, что
элемент х находится в отношении R с
элементом y и элемент y находится в
отношении R с элементом z , следует,
что и элемент x находится в отношении
R с элементом z.

20. Символическая запись свойства транзитивности

• R транзитивно на X xRy yRz xRz

21. Примеры транзитивных отношений

• - быть равным
• -быть кратным
• - быть параллельным на множестве
прямых
• - быть делителем
• - быть больше
• - быть подобным на множестве
треугольников

22. Свойство антитранзитивности

• Определение: отношение R на
множестве X называется
антитранзитивным, если выполняется
условие: из того, что элемент х
находится в отношении R с элементом
y и элемент y находится в отношении R
с элементом z , следует, что элемент x
НЕ находится в отношении R с
элементом z.

23. Примеры антитранзитивных отношений

• - быть перпендикулярным
• - быть больше в n раз
• - Быть длиннее в 3 раза на множестве
отрезков.

24. 4. Свойство связанности.

• Определение: отношение R на множестве X называется связанным, если
для любых элементов x и y из множества X выполняется условие: из того, что
х и y различны, следует, что либо x
находится в отношении R с элементом
y, либо элемент y находится в отношении R с элементом х.

25. Символическая запись свойства связанности

• R связано на множестве X x y xRy yRx

26. Примеры связанных отношений

• - быть больше на множестве
натуральных чисел
• - быть длиннее на множестве отрезков
• -

27. На графе

• 1 Отношение рефлексивности отмечается
петлей.
• 2 Отношение симметричности отмечается
стрелкой от элемента x к y и на оборот( туда,
сюда).
• 3. Отношение транзитивности отмечается
тремя стрелками: от x к y; от y к z и от x к z.
• 4. На графе связанного отношения любые
две вершины соединены стрелкой

28.

• Обобщим представление о
свойствах отношений на множестве

29.

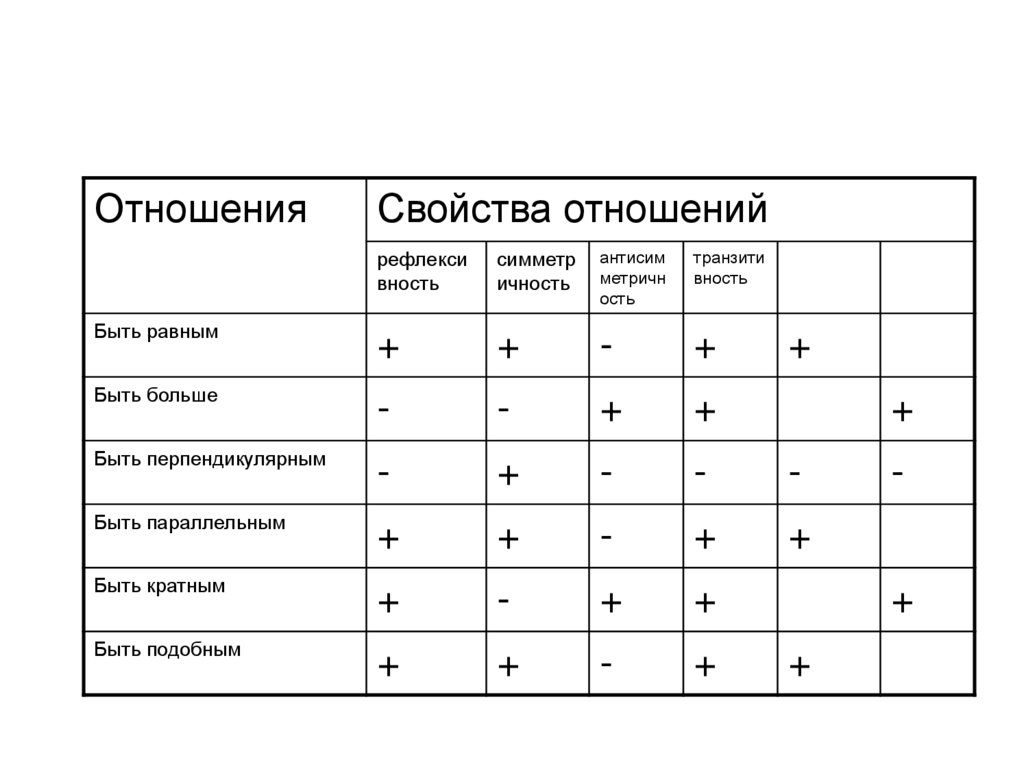
Отношения
Свойства отношений
рефлекси
вность
симметр
ичность
антисим
метричн
ость
транзити
вность
Быть равным
+
+
-
+
Быть больше
-
-
+
+
Быть перпендикулярным
-
+
-
-
-
Быть параллельным
+
+
-
+
+
Быть кратным
+
-
+
+
Быть подобным
+
+
-
+
+
+
-
+
+

30.

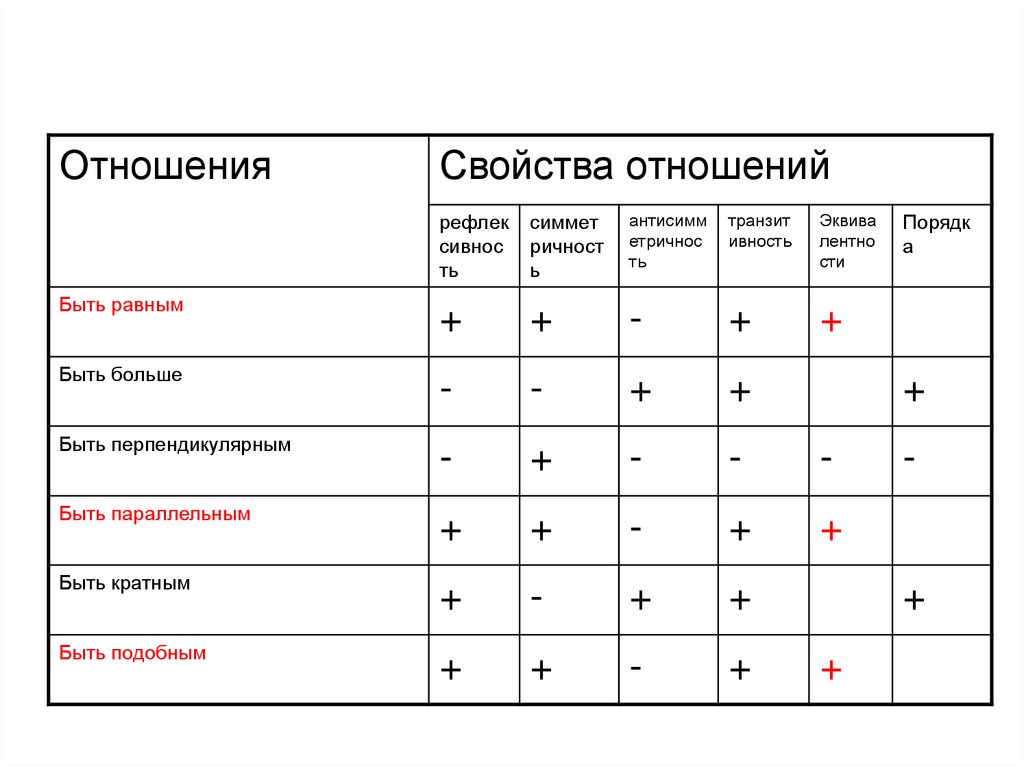
Отношения
Свойства отношений
рефлек
сивнос
ть
симмет
ричност
ь
антисимм
етричнос
ть
транзит
ивность
Эквива
лентно
сти
Быть равным
+
+
-
+
+
Быть больше
-
-
+
+
Быть перпендикулярным
-
+
-
-
-
Быть параллельным
+
+
-
+
+
Быть кратным
+
-
+
+
Быть подобным
+
+
-
+
Порядк
а
+
-
+
+

31.

Спасибо за внимание!