Свойства отношений

1.

Пусть R – бинарное отношение на множестве X и R X
1. Рефлексивность
Отношение R называется рефлексивным, если
для любого х Х выполняется xRx.

2.

Матрица такого отношения имеет единицы по главной диагонали.
Графически рефлексивное отношение задается графом:
Х
Отношения R = «=», R = « » являются рефлексивными.
В противном случае отношение называется антирефлексивным.
В этом случае на главной диагонали матрицы будут нули.

3.

2. Симметричность
Отношение R называется симметричным, если при
выполнении xRy выполняется и yRx, то есть справедливо:
xRy yRx.
Отношение R называется антисимметричным, если
из xRy и yRx, следует x = y.
У антисимметричного отношения Rij Rji и Rii = 1.

4.

Матрица симметричного отношения симметрична относительно
главной диагонали.
Граф:
Х
Y
Отношение R = «x и y являются чётными числами» - симметрично.

5.

3. Транзитивность
Отношение R называется транзитивным, если из
xRy и yRz, следует xRz,
то есть: xRy и yRz xRz.

6.

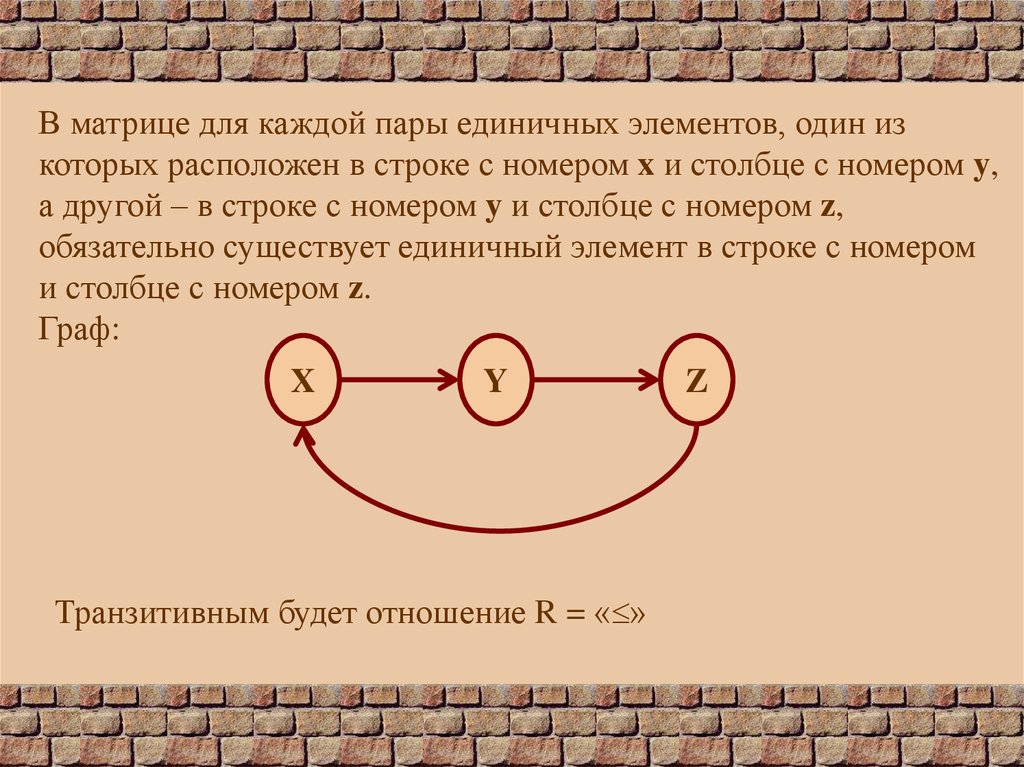
В матрице для каждой пары единичных элементов, один из
которых расположен в строке с номером x и столбце с номером y,
а другой – в строке с номером y и столбце с номером z,
обязательно существует единичный элемент в строке с номером
и столбце с номером z.
Граф:
X
Y
Транзитивным будет отношение R = « »
Z