Similar presentations:
Решение нелинейных уравнений
1.
Федеральное государственное бюджетное образовательное учреждениевысшего профессионального образования
«Ижевский государственный технический университет
имени М. Т. Калашникова»
Кафедра «АСОИУ»
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
Автор Исенбаева Е.Н., старший преподаватель
Ижевск
2013
2. РЕШЕНИЕ УРАВНЕНИЙ
Решить уравнение – значит найтимножество всех корней этого
уравнения.
При решении практических задач:
корни вычислены с заданной
степенью сложности-> задача
нахождения корней считается
решенной.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
2
3. КЛАССЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
В зависимости от того, какие функциивходят в уравнение f(x)=0, уравнения
разделяются на два больших класса:
– алгебраические,
– трансцендентные.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
3
4. КЛАССЫ НЕЛИНЕЙНЫХ ФУНКЦИЙ
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
4
5. АЛГЕБРАИЧЕСКАЯ ФУНКЦИЯ
Алгебраическая функция – функция,содержащая арифметические операции
(+, -, *, \ ) и возведение в степень с рациональным
показателем.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
5
6. Пример рациональной алгебраической функции
Рациональная алгебраическаяфункция:
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
6
7. ПРИМЕРЫ АЛГЕБРАИЧЕСКИХ ФУНКЦИЙ
Целая рациональная алгебраическая функция:Иррациональная алгебраическая функция:
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
7
8. АЛГЕБРАИЧЕСКАЯ ФУНКЦИЯ
Дробно-рациональная алгебраическая функция:Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
8
9. ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
Трансцендентные функции – всенеалгебраические функции: показательная
ax , логарифмическая logax ,
тригонометрические sinx, cosx, tgx, ctgx;
обратные тригонометрические arcsinx,
arccosx, arctgx, arcctgx и др.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
9
10. ЭТАПЫ НАХОЖДЕНИЙ КОРНЯ
Процесс нахождения приближенныхзначений корней уравнения
разбивается на 2 этапа:
1) отделение корней,
2) уточнение корней до заданной
степени точности.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
10
11. ЛОКАЛИЗАЦИЯ КОРНЕЙ
Отделить корни – это значит разбитьвсю область допустимых значений на
отрезки, в каждом из которых содержится
один корень.
Корень уравнения f(x)=0 считается
отделенным на [a, b], если на этом отрезке
уравнение f(x)=0 не имеет других корней.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
11
12. СПОСОБЫ ОТДЕЛЕНИЯ КОРНЕЙ
Отделение корней можнопроизвести двумя методами:
– графическим,
– аналитическим.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
12
13. ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ
I способ: Средствами машинной графикифункция f(x) представляется на дисплее и
приближенно определяются отрезки,
которым принадлежат корни xi.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
13
14. ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ
II способ: Все члены уравнения f(x)=0разбивают на 2 группы, т.е. представляют
уравнение в виде:
. Далее строят
графики функций
Абсциссы точек пересечения графиков
этих двух функций и служат корнями
данного уравнения.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
14
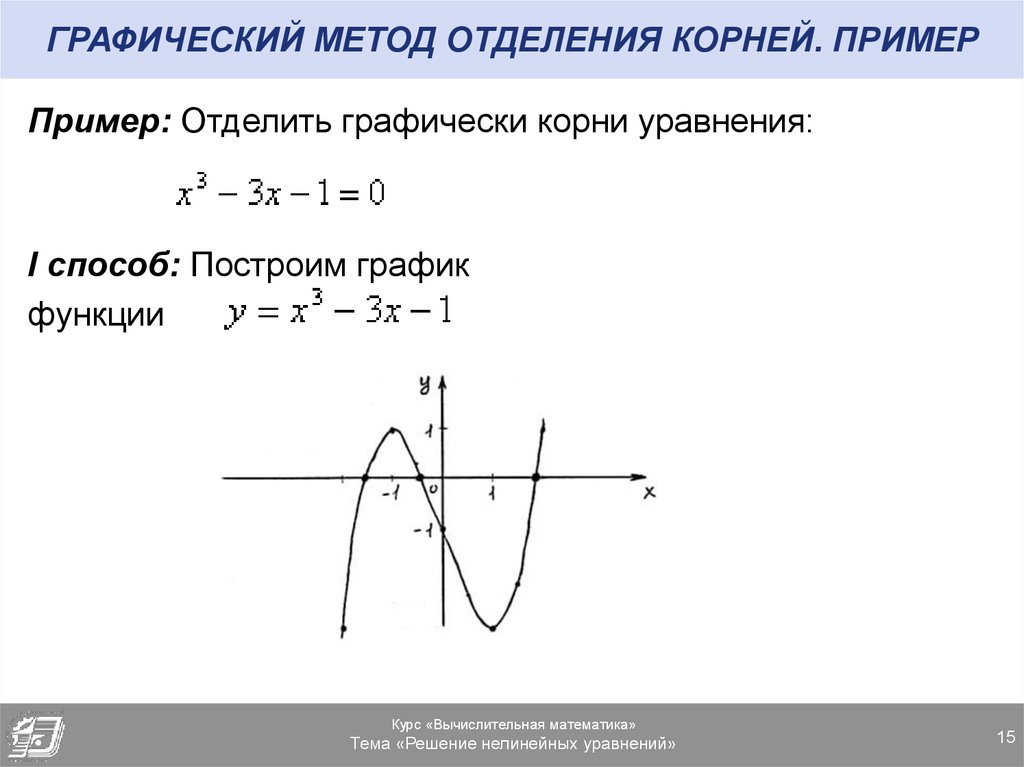
15. ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР
Пример: Отделить графически корни уравнения:I способ: Построим график
функции
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
15
16. ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР
II способ: Представим данное уравнение в видеи построим графики функций
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
16
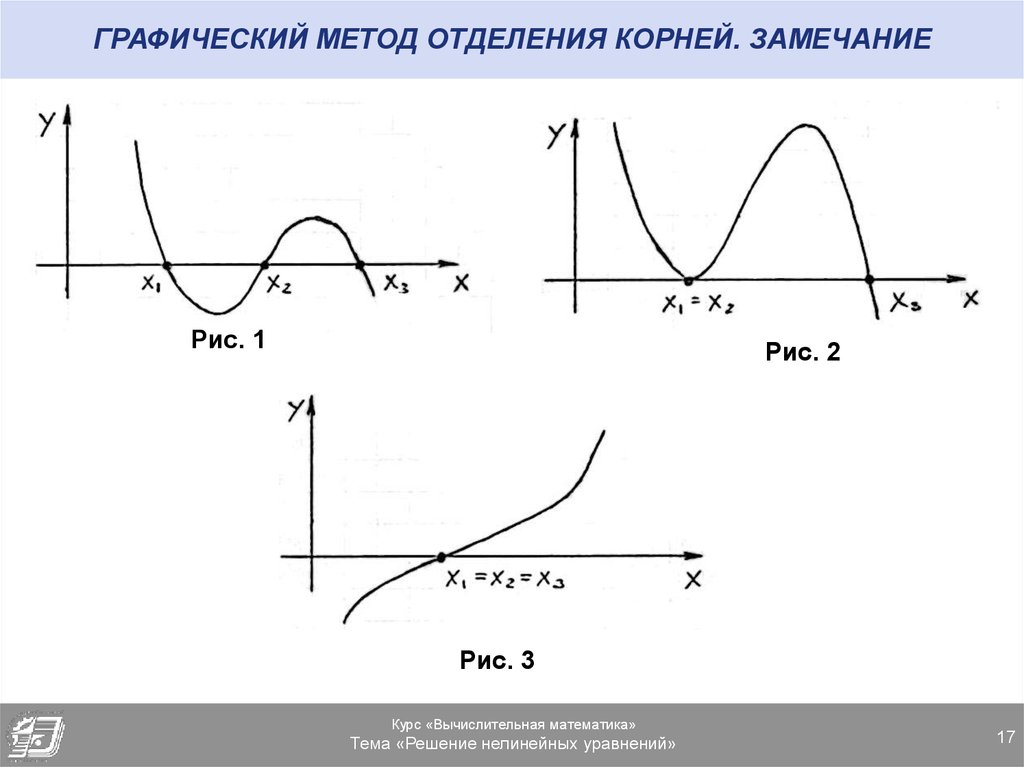
17. ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ. ЗАМЕЧАНИЕ
Рис. 1Рис. 2
Рис. 3
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
17
18. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ
Аналитически корни уравнения f(x)=0можно отделить, используя некоторые
свойства функций, изучаемые в курсе
математического анализа.
Теорема 1. Если функция f(x) непрерывна на
отрезке [a, b] и принимает на концах
этого отрезка значения разных знаков, то
внутри отрезка [a, b] существует, по
крайней мере, один корень уравнения
f(x)=0 .
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
18
19. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ
Теорема 2. Если функция f(x) непрерывнаи монотонна на отрезке [a, b] и принимает
на концах отрезка значения разных
знаков, то внутри отрезка [a, b]
содержится корень уравнения f(x)=0 , этот
корень единственный.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
19
20. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ
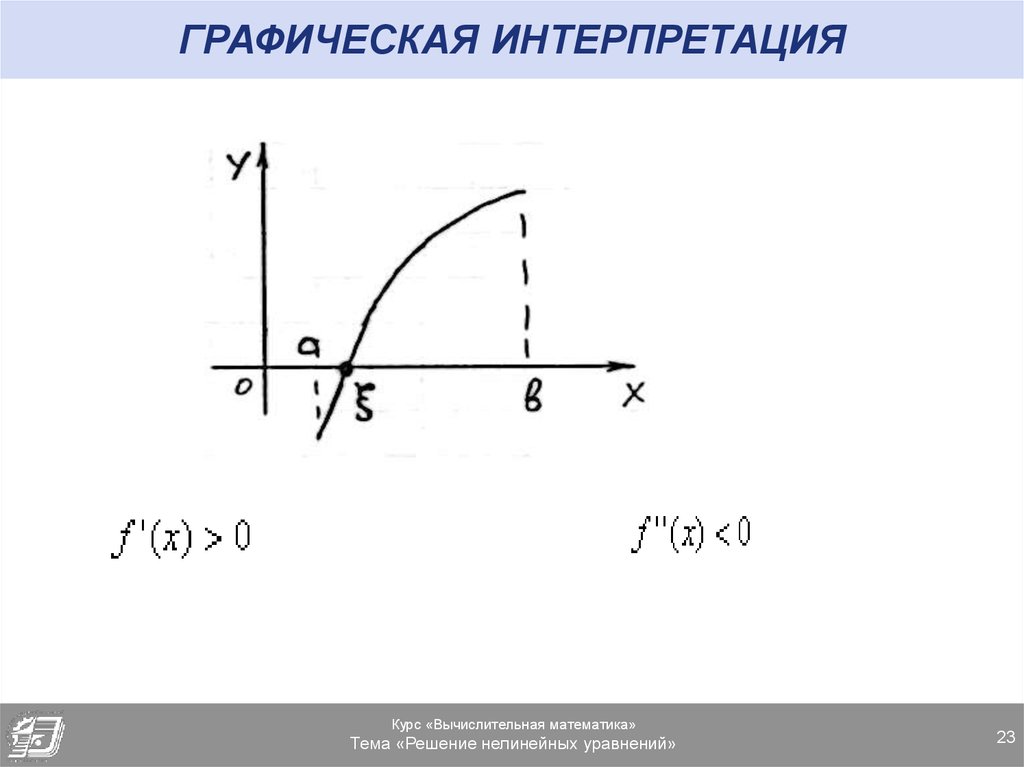
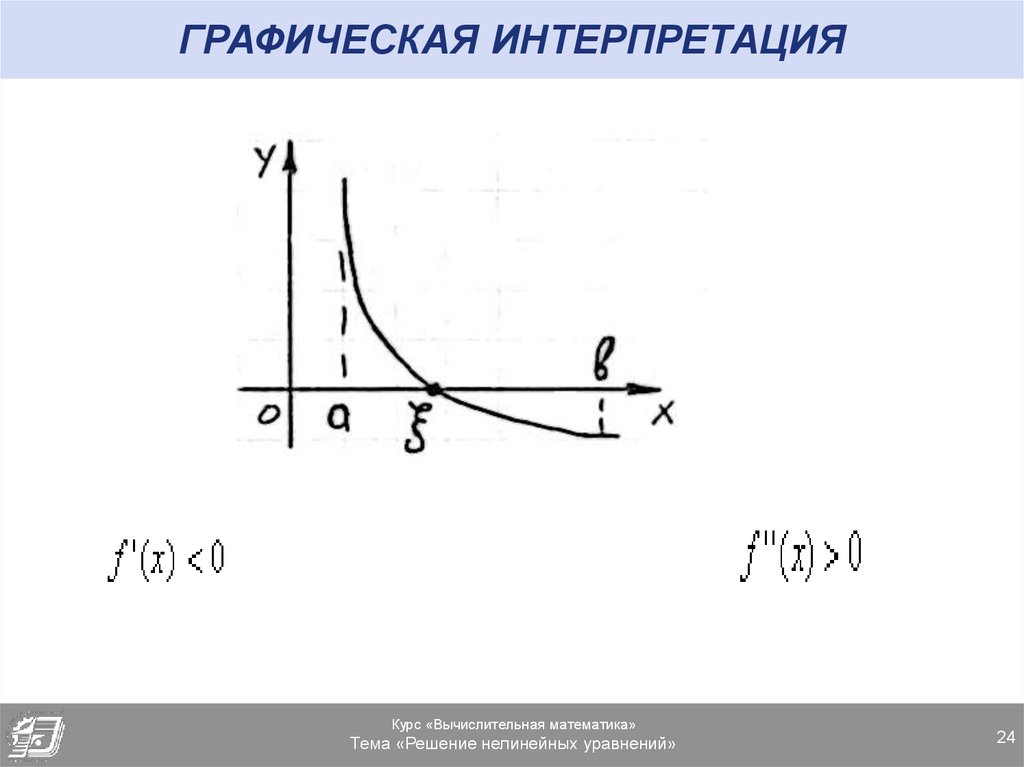
Теорема 3. Если функция f(x) непрерывна наотрезке [a, b] и принимает на концах
отрезка значения разных знаков, а
производная f’(x) сохраняет знак внутри
отрезка, то внутри отрезка существует
корень уравнения f(x)=0 и притом
единственный.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
20
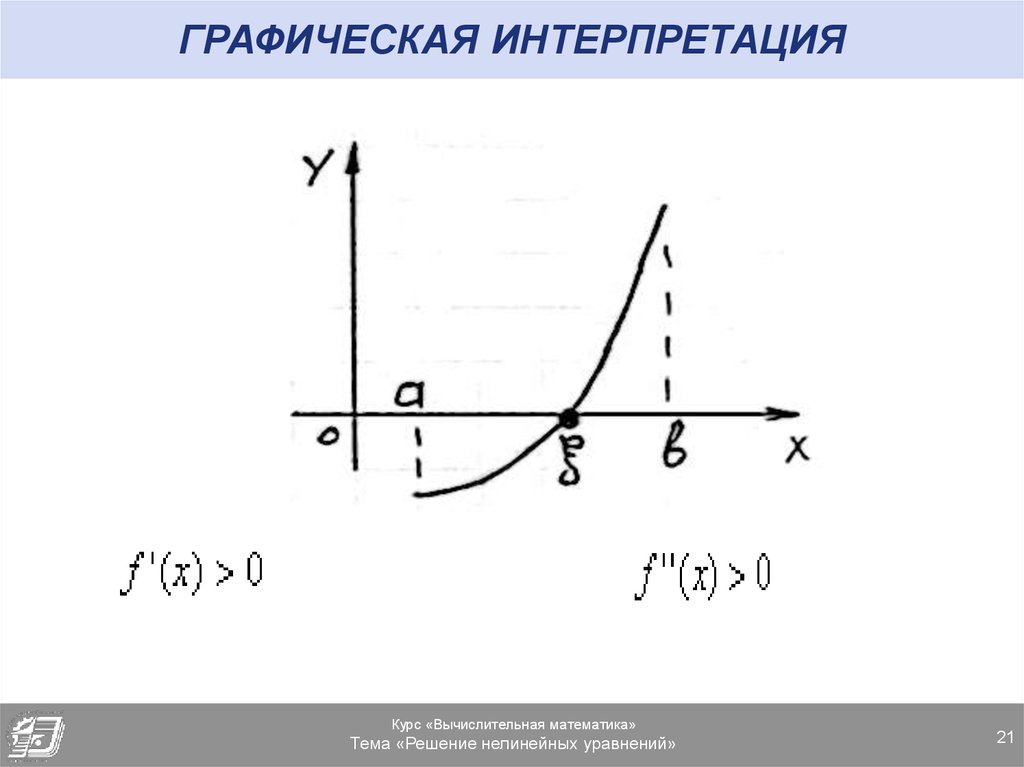
21. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
21
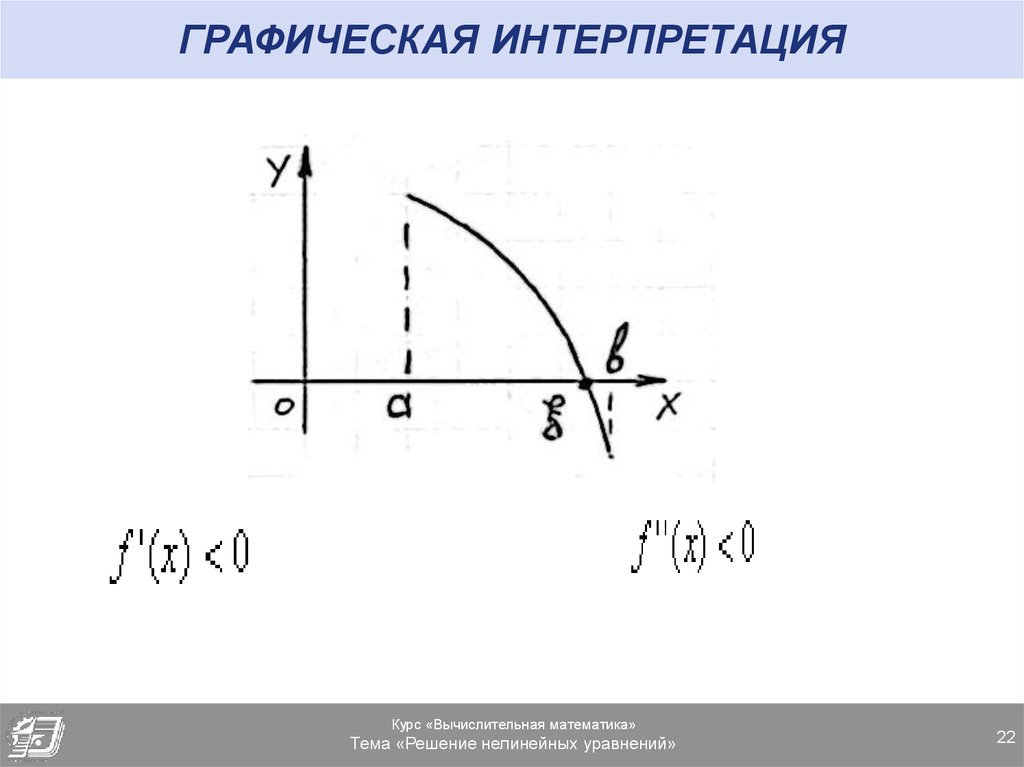
22. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
22
23. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
23
24. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
24
25. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ
Для того чтобы определить наибольшее инаименьшее значение функции на отрезке, надо:
1) Определить критические точки функции, т.е.
точки, в которых первая производная функции равна
нулю или не существует, но функция сохраняет
непрерывность.
2) Вычислить значения функции в критических
точках и на концах отрезка [a, b].
3) Наибольшее из значений, найденных в п.2, будет
наибольшим, а наименьшее – наименьшим
значением функции на отрезке.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
25
26. ПОРЯДОК ДЕЙСТВИЙ ДЛЯ ОТДЕЛЕНИЯ КОРНЕЙ АНАЛИТИЧЕСКИМ МЕТОДОМ
1) Находят f’(x).2) Составляют таблицу знаков функции f(x), полагая
х равным:
а) критическим значениям (корням) производной
или ближайшим к ним
б) граничным значениям (исходя из ОДЗ
неизвестного).
3) Определяют интервалы, на концах которых
функция принимает значения противоположных
знаков. Внутри этих интервалов содержится по
одному и только по одному корню.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
26
27. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
27
28. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР
• Составим таблицу знаков функции f(x),полагая х равным:
• а) критическим значениям (корням
производной) или ближайшим к ним;
• б) граничным значениям
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
28
29. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР
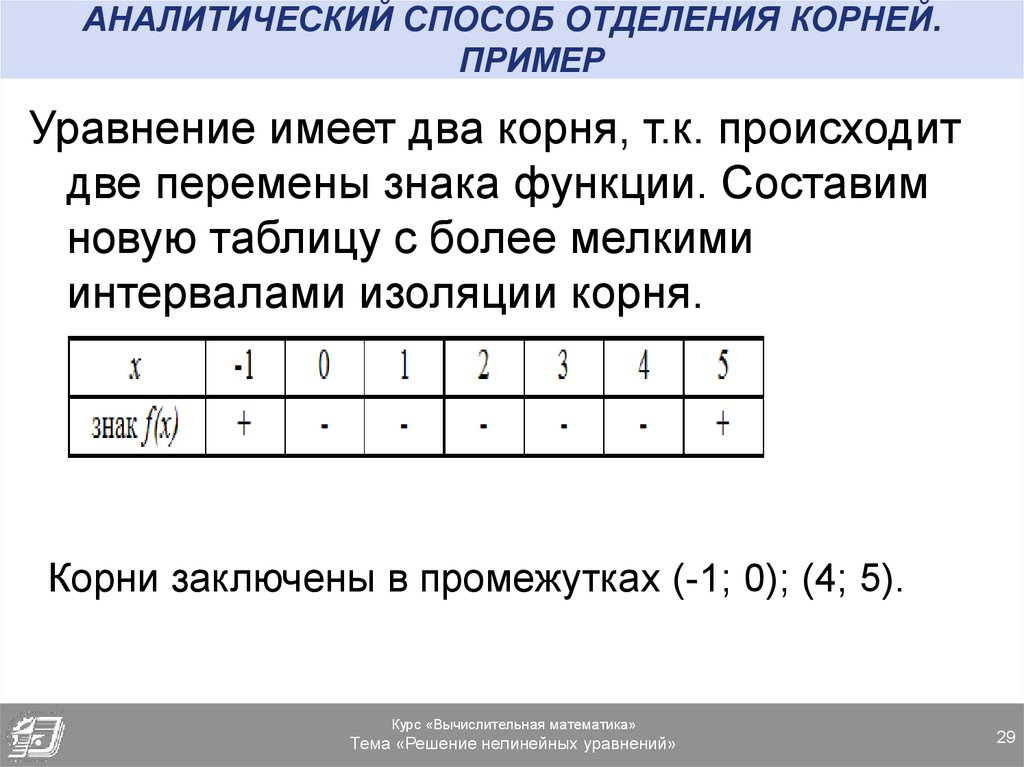
Уравнение имеет два корня, т.к. происходитдве перемены знака функции. Составим
новую таблицу с более мелкими
интервалами изоляции корня.
Корни заключены в промежутках (-1; 0); (4; 5).
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
29
30. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
Теорема 1: (о числе корней алгебраическогоуравнения
действительные числа (1)
Алгебраическое уравнение n-й степени
имеет ровно n корней, действительных или
комплексных, при условии, что каждый
корень считается столько раз, какова его
кратность.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
30
31. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
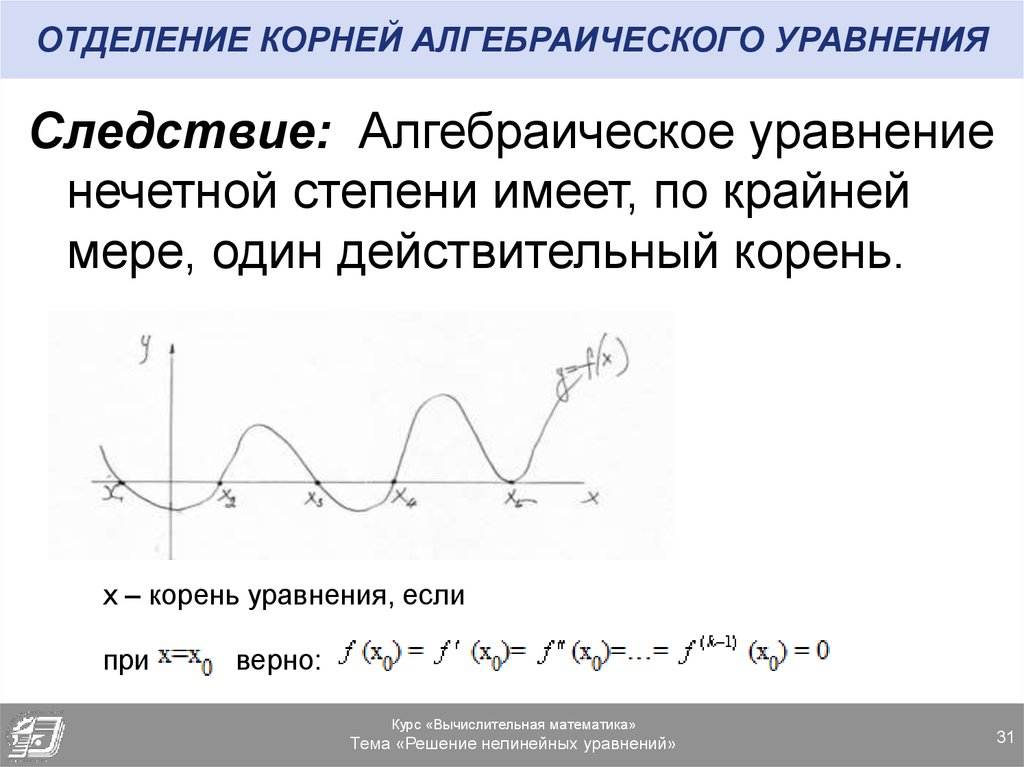
Следствие: Алгебраическое уравнениенечетной степени имеет, по крайней
мере, один действительный корень.
х – корень уравнения, если
при
верно:
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
31
32. КРАТНОСТЬ КОРНЯ
• Число x есть корень уравнения (1)кратности k, если при x=x0 вместе с
функцией f(x) обращаются в нуль ее
производные до (k-1) го порядка
включительно.
• Простой корень- корень кратности k=1.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
32
33. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
33
34. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
Теорема 3: (теорема Лагранжа о верхней границеположительных корней уравнения (1)).
Пусть an > 0 и ai – первый отрицательный
коэффициент в последовательности
C – наибольшая из абсолютных величин
отрицательных коэффициентов. Тогда за
верхнюю границу положительных корней
уравнения принимают число:
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
34
35. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
Теорема 4: (о нижних и верхних границахположительных и отрицательных корней
алгебраического уравнения).
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
35
36. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
Тогда положительные корнии отрицательные корни
уравнения(1) удовлетворяют неравенствам:
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
36
37. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
Теорема 5: (теорема Декарта о количестведействительных корней алгебраического
уравнения).
Число S1 положительных корней (с учетом
их кратности) алгебраического уравнения
равно числу перемен знаков в
последовательности коэффициентов
(коэффициенты = 0 не
учитываются) многочлена
или меньше
этого числа на четное число.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
37
38. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
Число S2 отрицательных корней (сучетом их кратности) алгебраического
уравнения
равно числу перемен знаков в
последовательности коэффициентов
многочлена
или меньше этого
числа на четное число.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
38
39. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
Теорема 6: (теорема Гюа о необходимомусловии действительности всех корней
алгебраического уравнения).
Если алгебраическое уравнение имеет все
действительные корни, то квадрат каждого
некрайнего коэффициента больше
произведения двух его соседних
коэффициентов.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
39
40. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ. ПРИМЕР
Отделить корни алгебраического уравненияпо Теоремам.
Согласно Следствию Теоремы 1 уравнение имеет
3 корня, среди которых, по крайней мере один
действительный.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
40
41. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ. ПРИМЕР
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
41
42. ЛОКАЛИЗАЦИЯ ПОЛОЖИТЕЛЬНЫХ КОРНЕЙ
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
42
43. ЛОКАЛИЗАЦИЯ ПОЛОЖИТЕЛЬНЫХ КОРНЕЙ
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
43
44. ЛОКАЛИЗАЦИЯ ОТРИЦАТЕЛЬНЫХ КОРНЕЙ
• Рассчитаем границы отрицательныхкорней по Теоремам 3 и 4:
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
44
45. ЛОКАЛИЗАЦИЯ ОТРИЦАТЕЛЬНЫХ КОРНЕЙ
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
45
46. Нахождение числа положительных корней уравнения
Определим количество положительныхкорней по Теореме 5 уравнения:
=
Коэффициенты многочлена: 1,-1,-9, 9.
Количество перемен знака- 2→ количество
положительных корней уравнения- два
или их нет.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
46
47. Нахождение числа отрицательных корней уравнения
Определим количество отрицательныхкорней уравнения. Для уравнения
выпишем коэффициенты: -1, -1, 9, 9.
Количество перемен знака- 1 → число
отрицательных корней- один.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
47
48. Исследование структуры корней
• По Теореме Гюа исследуем структурукорней по коэффициентам уравнения:
Необходимое условие действительности
всех корней уравнения выполняется.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
48
49. Уточнение корней
Уточнение корней – это доведениеотделенных корней до заданной
степени точности.
Второй этап решения алгебраических и
трансцендентных уравнений.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
49
50. УТОЧНЕНИЕ КОРНЕЙ
Пусть дано уравнение f(x)=0, где f(x) –непрерывная функция. Требуется найти корень
этого уравнения с точностью , где некоторое положительное достаточно малое
число.
Будем считать, что корень отделен и находится
на отрезке [a,b], т.е. f(a)*f(b)<0, причем |b-a|> .
Здесь f(x) – непрерывная функция.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
50
51. МЕТОДЫ УТОЧНЕНИЯ КОРНЕЙ
1. МЕТОДЫ ДИХОТОМИИ-Метод половинного деления
-Метод хорд
2. Метод простых итераций
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
51
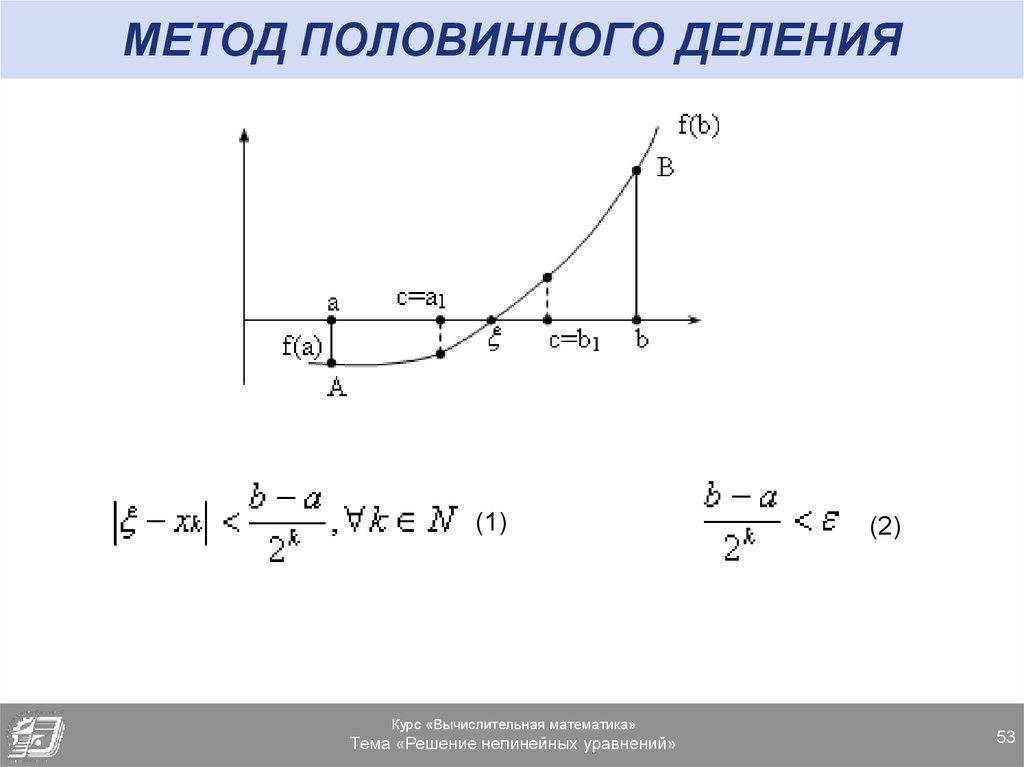
52. МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ
Возьмем на отрезке [a,b] промежуточную точку так, чтобы онаявлялась серединой отрезка [a,b], т.е. c=(a+b)/2.
Алгоритм метода
1. Задать концы отрезка [a,b], функцию f, малое
число >0, вычислить (или ввести) f(a).
2. Вычислить c=(a+b)/2.
3. Если (b-a)<2, то положить c и останов
4. Вычислить f(c)
5. Если f(a)*f(c)<0, положить b=c и вернуться к
шагу 2, иначе a=c, f(a)=f(c) и вернуться к шагу 2.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
52
53. МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ
(1)Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
(2)
53
54. Априорная оценка метода половинного деления
Априорная оценка позволяет предварительнорассчитать примерное количество
шагов(итераций), достаточное для получения
корня с заданной степенью точности Ɛ. Для
этого находим наименьшее натуральное
решение неравенства (2).
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
54
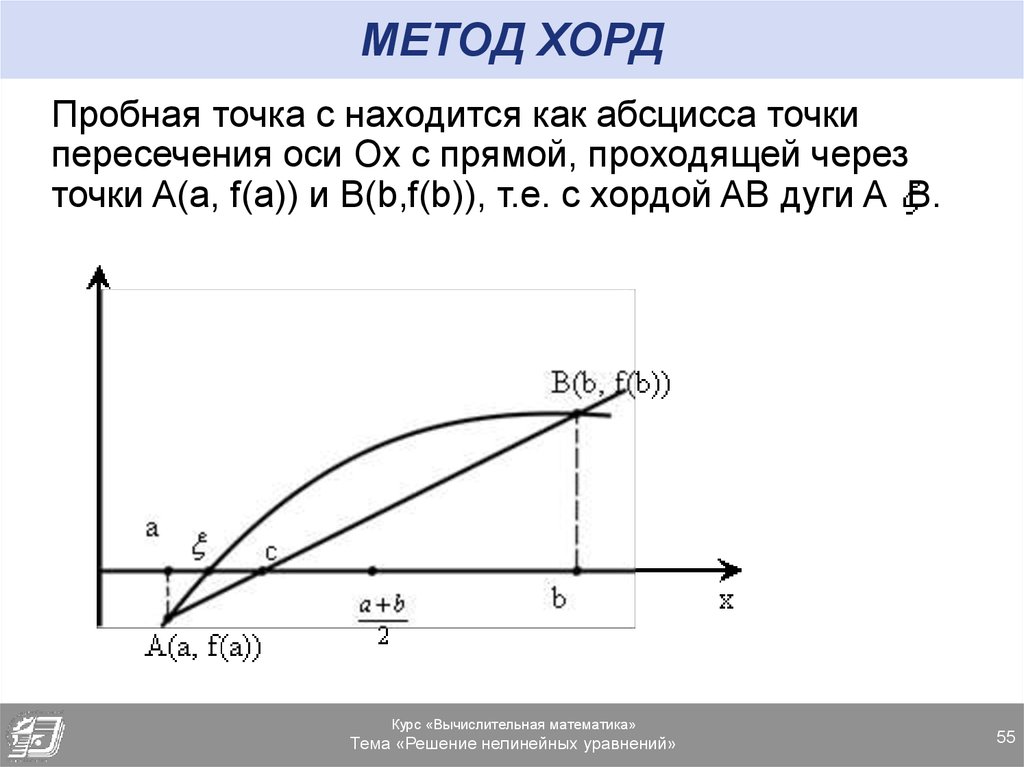
55. МЕТОД ХОРД
Пробная точка c находится как абсцисса точкипересечения оси Ox с прямой, проходящей через
точки A(a, f(a)) и B(b,f(b)), т.е. с хордой AB дуги A B.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
55
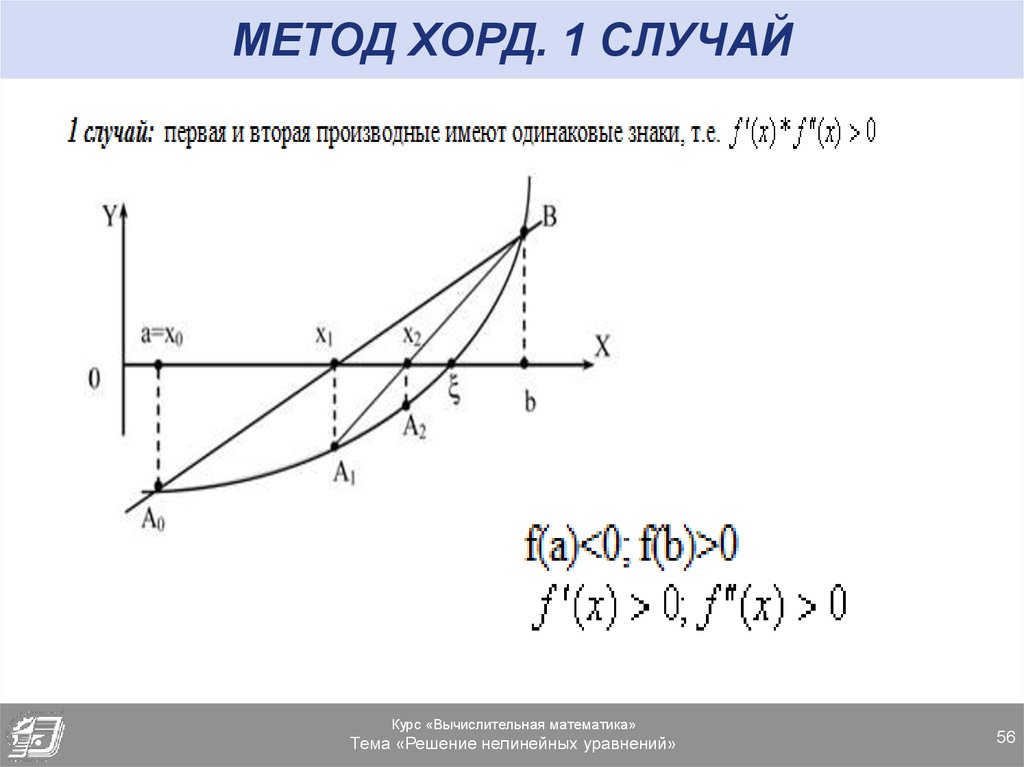
56. МЕТОД ХОРД. 1 СЛУЧАЙ
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
56
57.
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
57
58. МЕТОД ХОРД. 1 СЛУЧАЙ
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
58
59. МЕТОД ХОРД. 1 СЛУЧАЙ
(2)Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
59
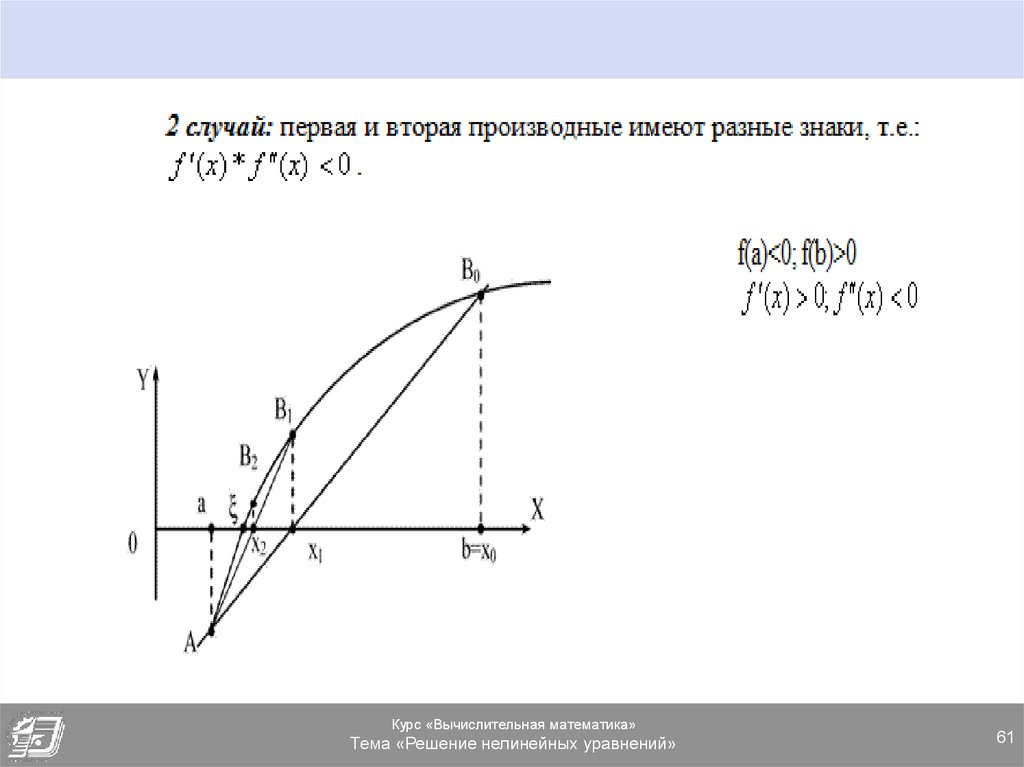
60. МЕТОД ХОРД. 2 СЛУЧАЙ
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
60
61.
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
61
62. МЕТОД ХОРД. 2 СЛУЧАЙ
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
62
63. МЕТОД ХОРД. 2 СЛУЧАЙ
В общем случае:(3)
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
63
64. МЕТОД ХОРД
Выбор формулы (2) или (3) можноосуществить, пользуясь простым
правилом: неподвижным концом
отрезка является тот, для которого
знак функции совпадает со знаком
второй производной.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
64
65. МЕТОД ХОРД
→ неподвижен конец b,в качестве начального приближенияконец a. При этом используется расчетная
формула (2).
→ неподвижен конец a,
в качестве начального приближенияконец b. При этом используется расчетная
формула (3).
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
65
66. МЕТОД ХОРД. УСЛОВИЕ ОСТАНОВА ПРОЦЕССА
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
66
67. МЕТОД ХОРД. УСЛОВИЕ ОСТАНОВА ПРОЦЕССА
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
67
68. МЕТОД ХОРД. ПРИМЕР
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
68
69. МЕТОД ХОРД. ПРИМЕР
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
69
70. МЕТОД ХОРД. ПРИМЕР
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
70
71. МЕТОД ХОРД. ПРИМЕР
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
71
72. МЕТОД ХОРД. ПРИМЕР
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
72
73. МЕТОД ХОРД. ПРИМЕР
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
73
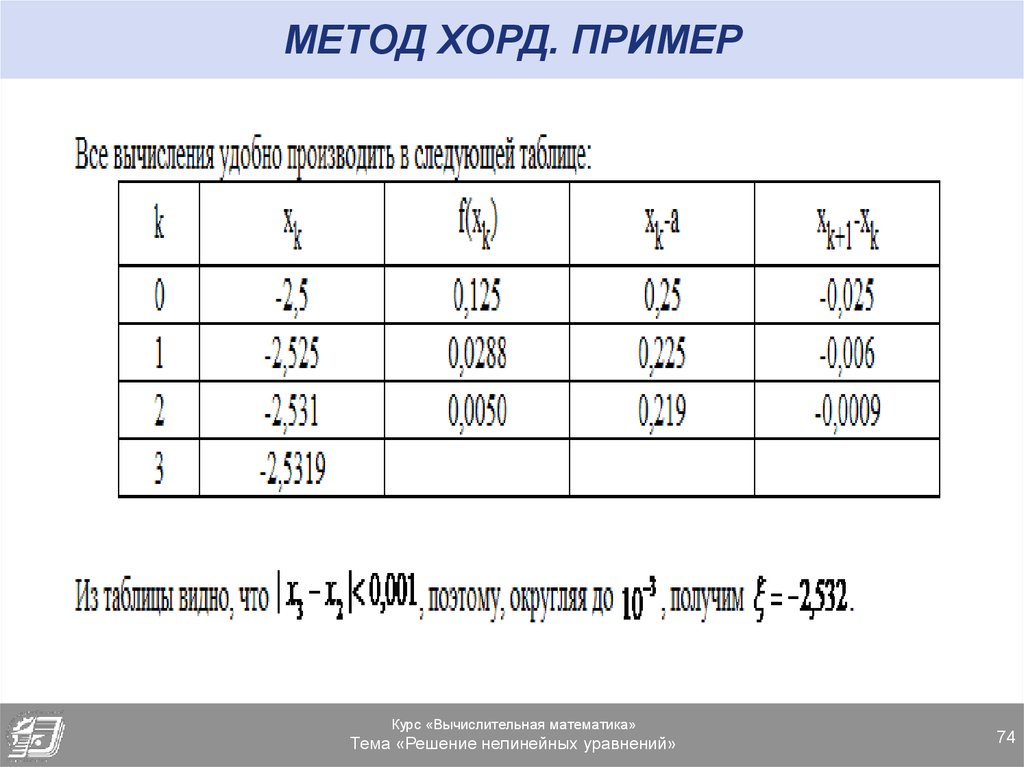
74. МЕТОД ХОРД. ПРИМЕР
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
74
75. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ
Дано(1)
Если существует
непрерывна, то получим
(2)
и функция
Существование и единственность корня уравнения
основывается на принципе сжимающих
отображений (принципе неподвижной точки).
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
75
76. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
76
77. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ
[a, b] [a1, b1] [a2, b2] … [ak, bk ] …Возрастающая функция
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
77
78. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ
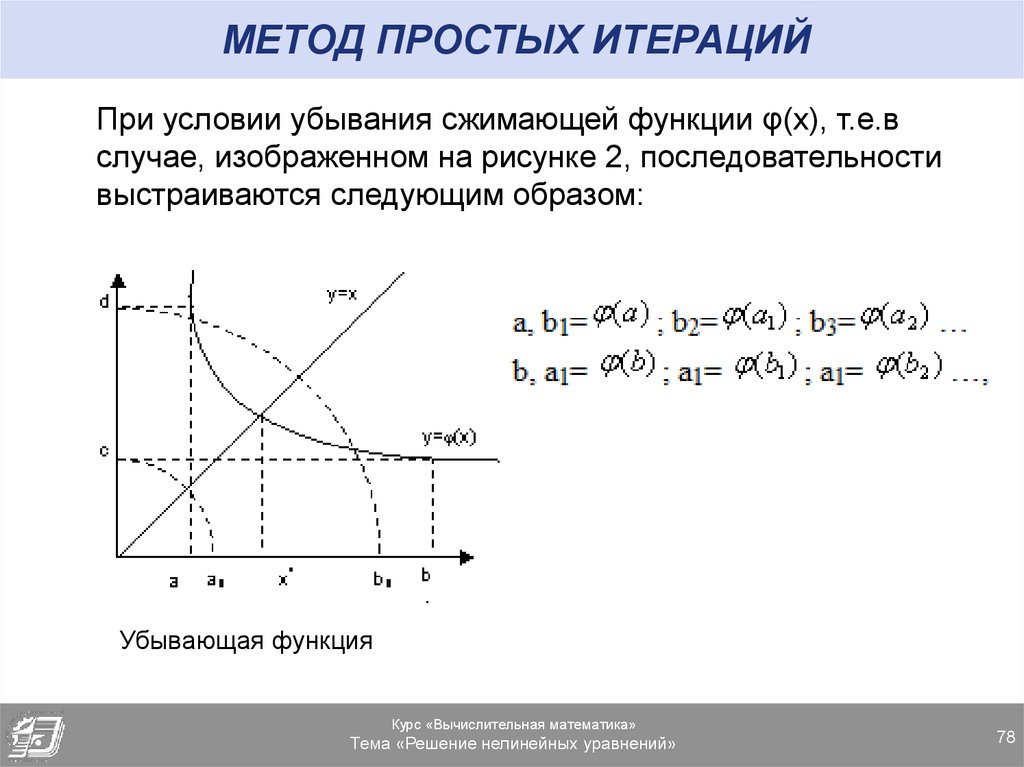
При условии убывания сжимающей функции φ(x), т.е.вслучае, изображенном на рисунке 2, последовательности
выстраиваются следующим образом:
Убывающая функция
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
78
79. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
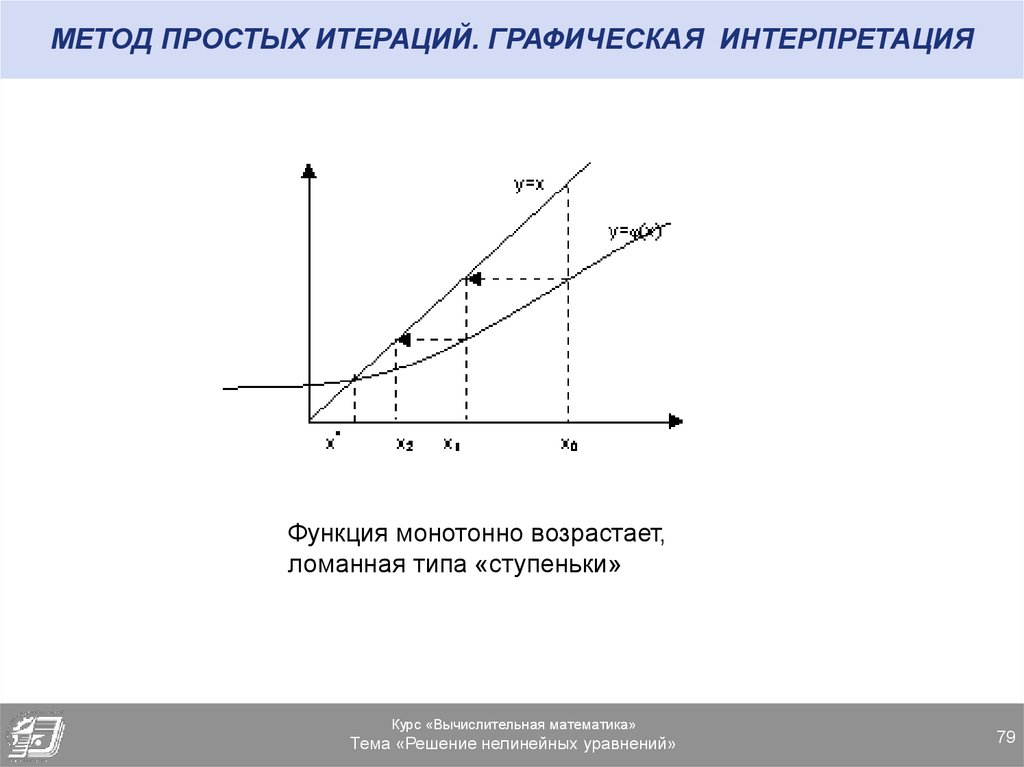
Функция монотонно возрастает,ломанная типа «ступеньки»
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
79
80. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
Функция монотонно убывает,ломанная типа «спираль»
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
80
81. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ
Выводы:На некотором промежутке [a,b] функция φ(x) удовлетворяет
условиям сжатия, зафиксированным в определении →
1. уравнение x= φ(x) имеет и притом единственный корень x*є[a,b] ;
2. к этому корню со скоростью геометрической прогрессии сходится
определяемая МПИ последовательности (xk), начинающая с
x0є[a,b], причем скорость сходимости тем выше, чем меньше
коэффициент сжатия qє(0,1);
3. функция φ(x) монотонно возрастает на [a, b] → приближения xk к x0
также будут монотонными;
4. φ(x) убывает → процесс порождает двустороннее приближение к
корню x*.
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
81
82. УСЛОВИЯ СХОДИМОСТИ ИТЕРАЦИОННОГО ПРОЦЕССА
тогда итерационный процесс сходится, независимо отвыбора начального приближения, к единственному и
однократному корню на отрезке [a, b].
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
82
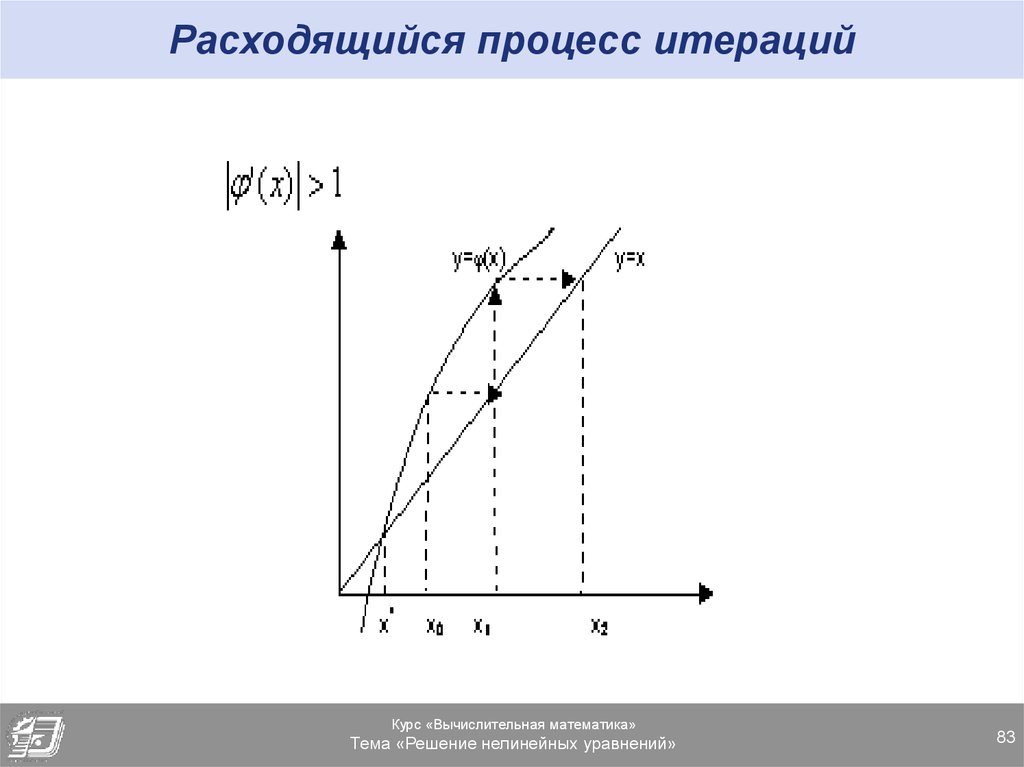
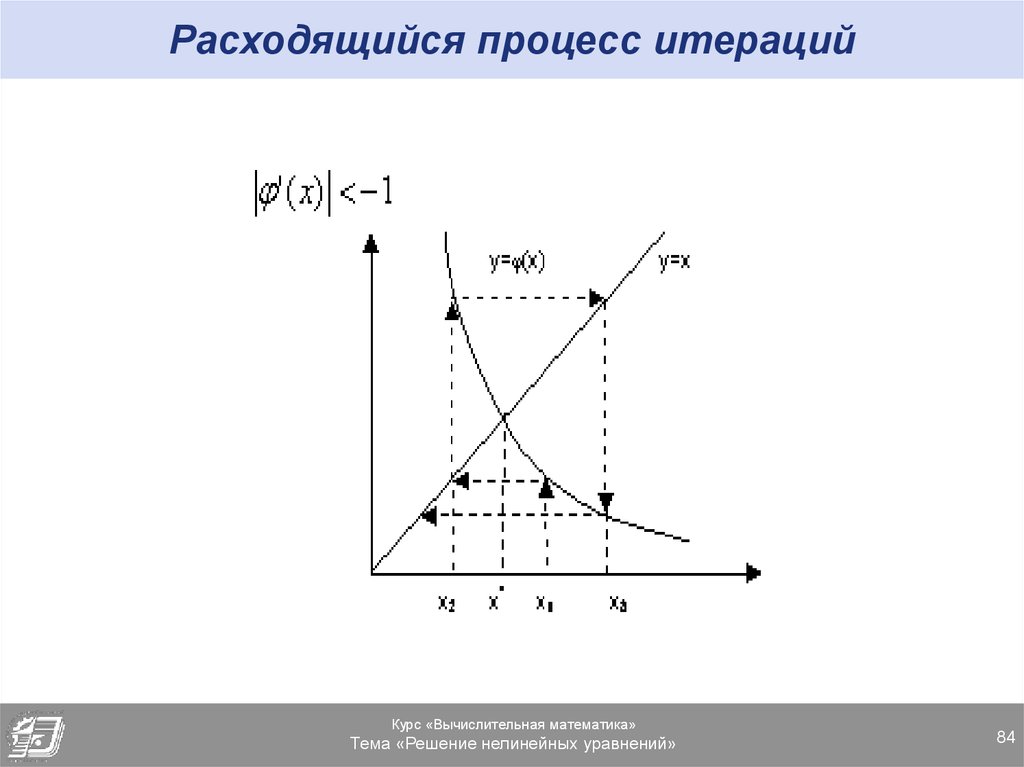
83. Расходящийся процесс итераций
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
83
84. Расходящийся процесс итераций
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
84
85. АПОСТЕРИОРНАЯ ОЦЕНКА
Используется для остановки итерационного процессаКурс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
85
86. Априорная оценка
Используется для предварительного расчетаколичества операций
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
86
87. СПОСОБЫ ПРЕОБРАЗОВАНИЯ УРАВНЕНИЯ (1) К ВИДУ (2)
1. Заменяем f(x)=0 на равносильноеx=x+cf(x), c=const≠0
φ(x)=x
Находим с є [a,b]
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
87
88. СПОСОБЫ ПРЕОБРАЗОВАНИЯ УРАВНЕНИЯ (1) К ВИДУ (2)
2. Заменяем f(x)=0 на равносильноеЗнак выбирается из условия
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
88
89. СПОСОБЫ ПРЕОБРАЗОВАНИЯ УРАВНЕНИЯ (1) К ВИДУ (2)
3.Выражаем x из : f(x)=0x=φ(x);
Курс «Вычислительная математика»
Тема «Решение нелинейных уравнений»
89
90. ПРИМЕР
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
90
91. ПРИМЕР
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
91
92. ПРИМЕР
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
92
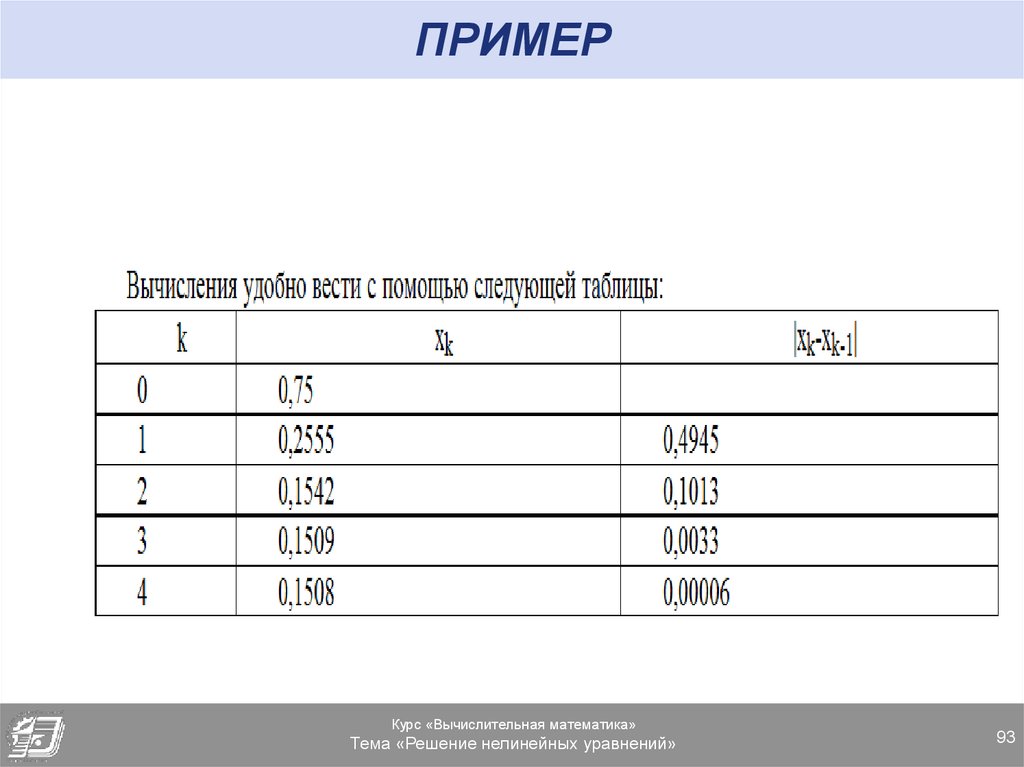
93. ПРИМЕР
Курс «Вычислительная математика»Тема «Решение нелинейных уравнений»
93
94.
СПАСИБО ЗА ВНИМАНИЕ© ФГБОУ ВПО ИжГТУ имени М.Т. Калашникова, 2013
© Исенбаева Елена Насимьяновна, 2013












































































 mathematics
mathematics








