1661a035-3780-457f-b16f-1718e0f4d2a2

1.

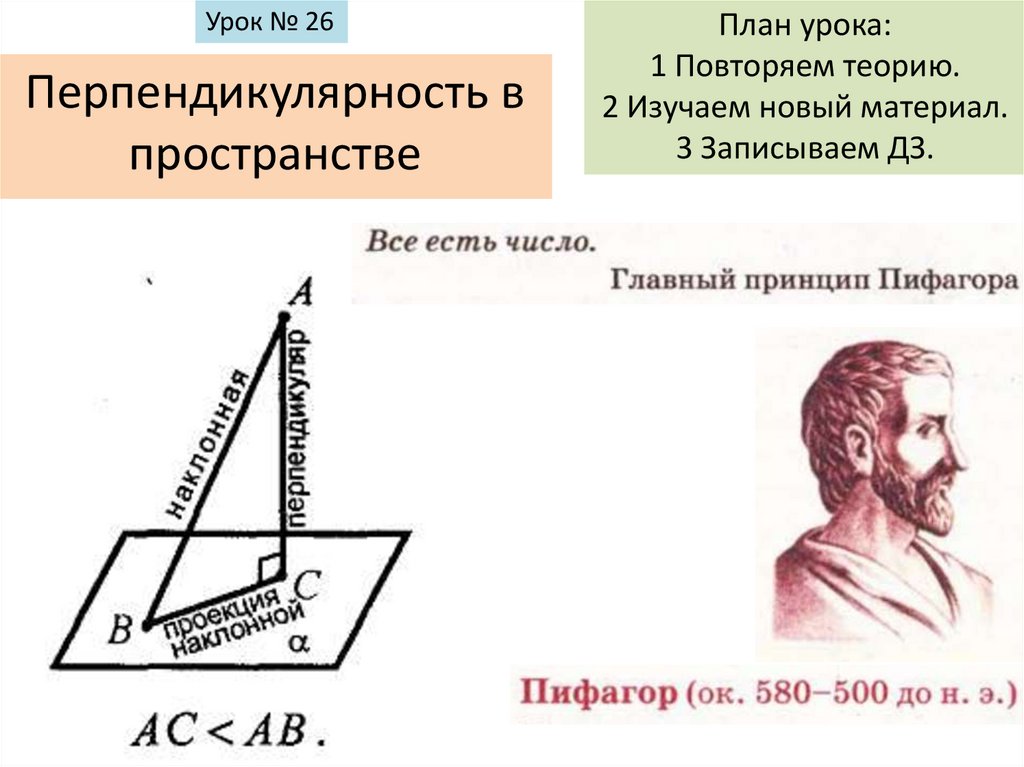
Урок № 26
Перпендикулярность в
пространстве
План урока:
1 Повторяем теорию.
2 Изучаем новый материал.
3 Записываем ДЗ.

2.

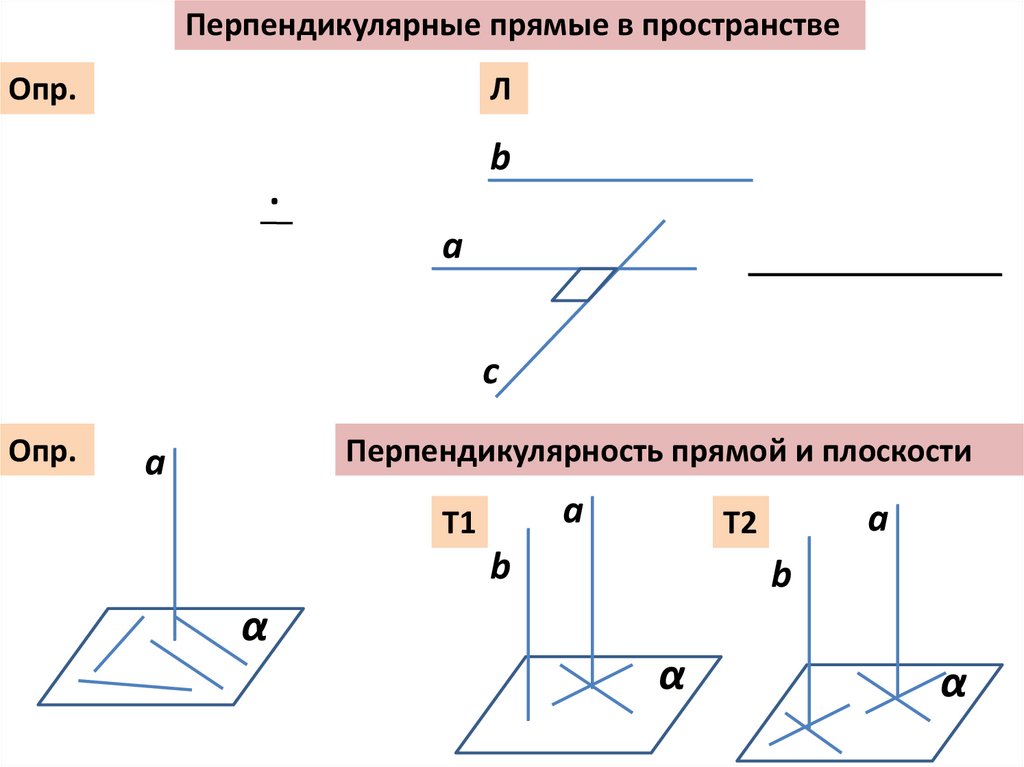
Перпендикулярные прямые в пространстве
Опр.
Л
·
b
a
c
Опр.
Перпендикулярность прямой и плоскости
a
a
Т1
a
Т2
b
b
α
α
α

3.

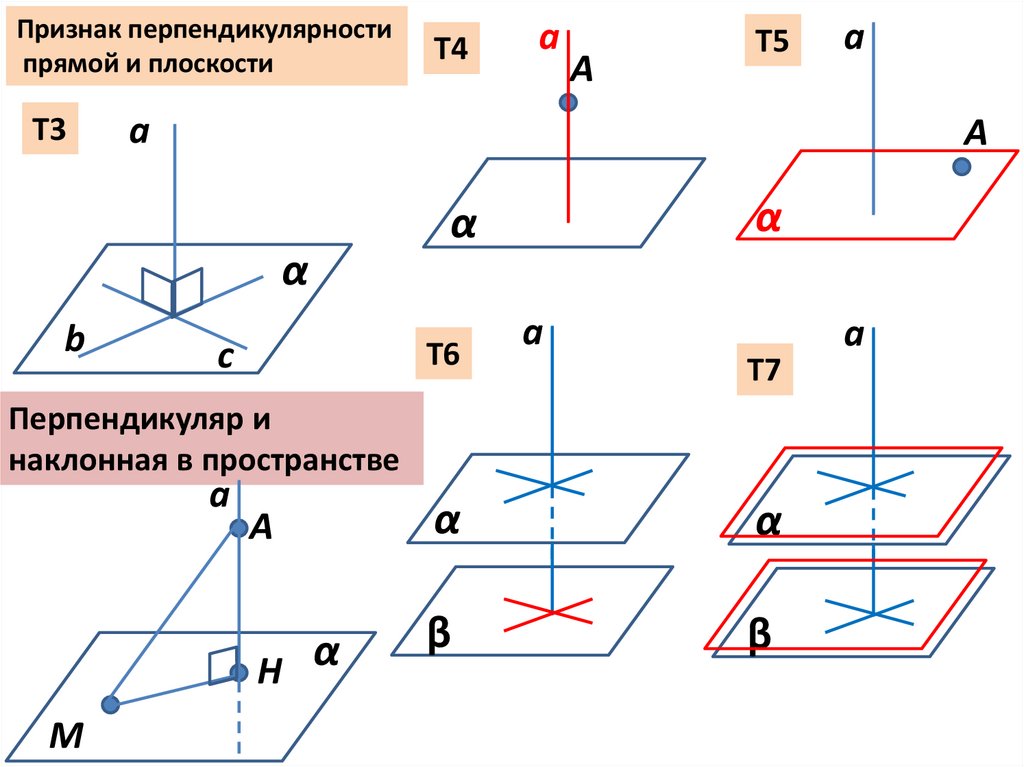
Признак перпендикулярности
прямой и плоскости
Т3
Т4
a
А
Т5
a
a
А
α
α
α
b
с
Т6
a
Т7
Перпендикуляр и
наклонная в пространстве
a
М
А
α
α
Н α
β
β
a

4.

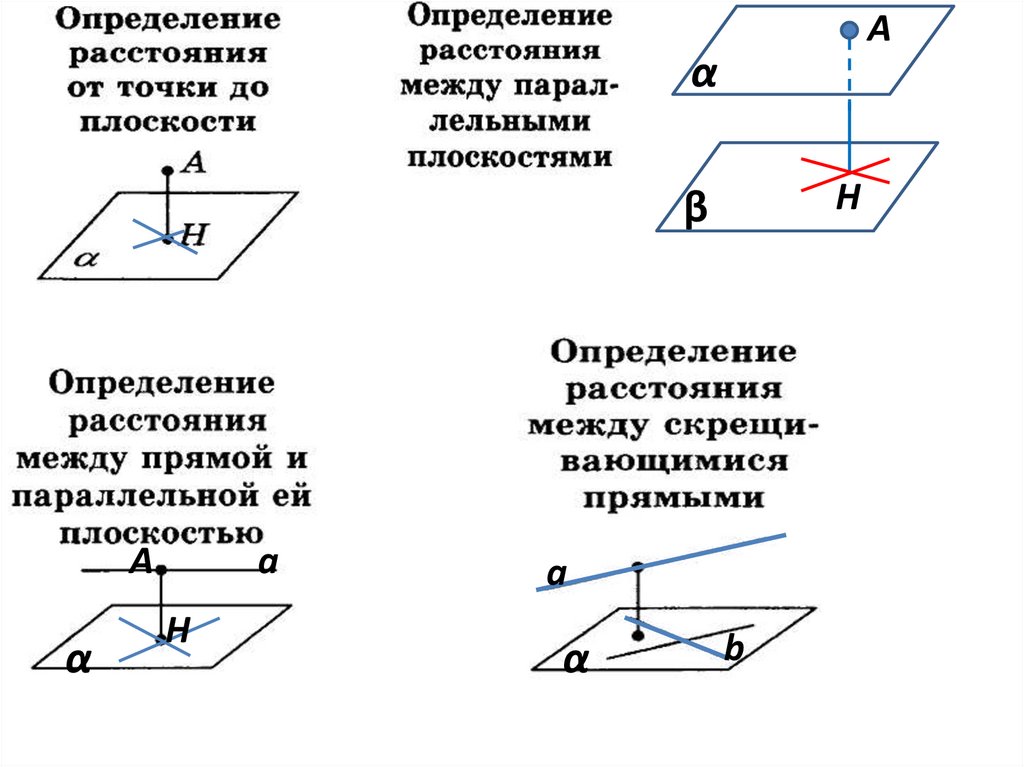
A
α
H
β
A
α
a
H
a
α
b

5.

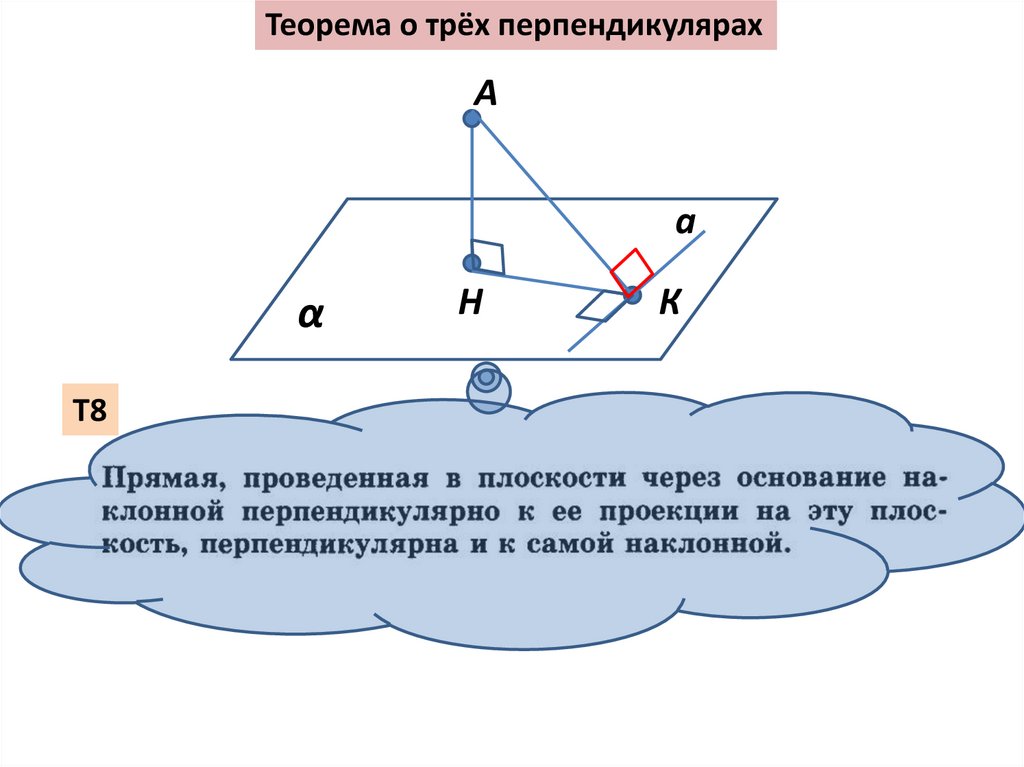
Теорема о трёх перпендикулярах
А
a
α
Т8
Н
К

6.

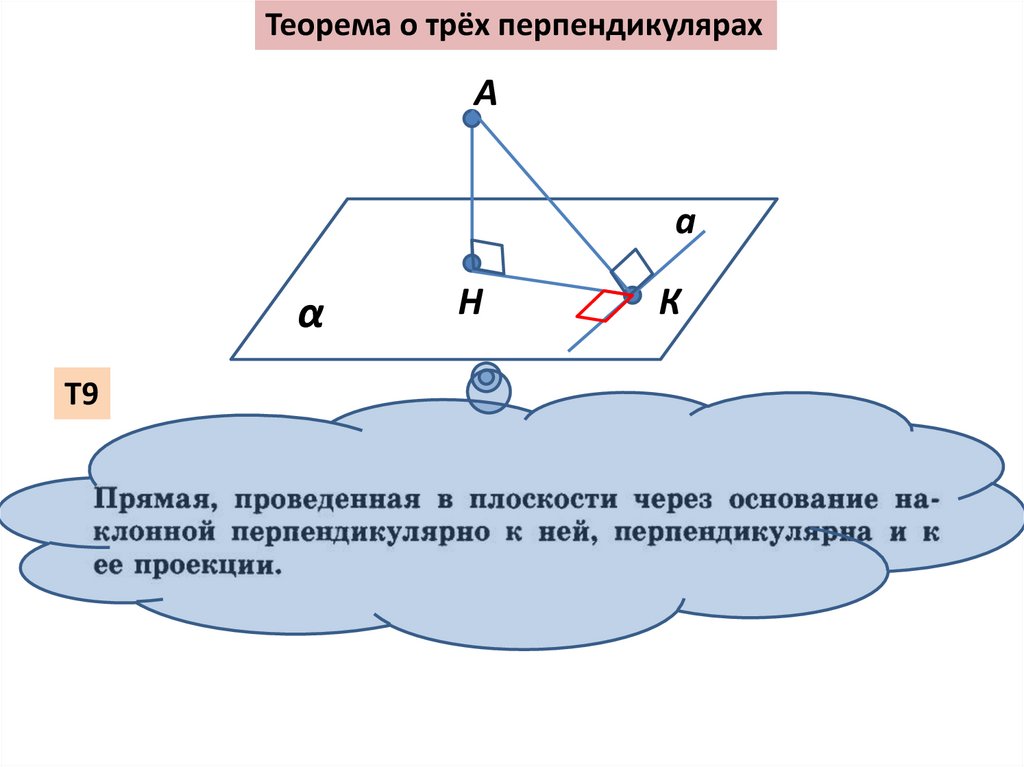
Теорема о трёх перпендикулярах
А
a
α
Т9
Н
К

7.

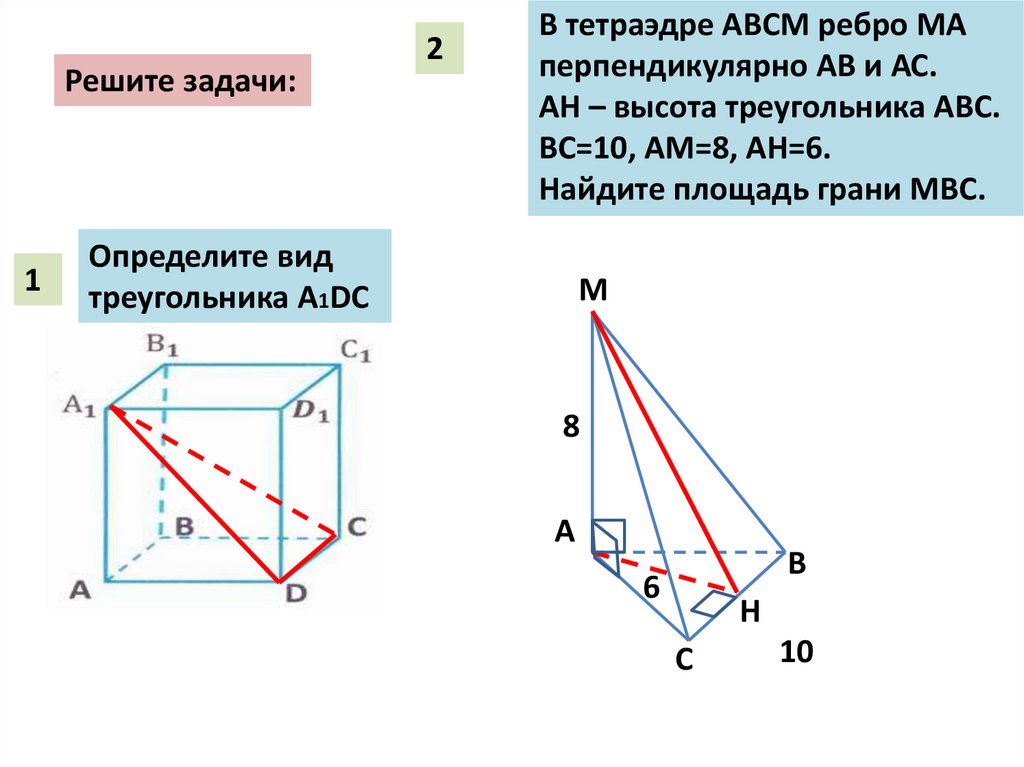
Решите задачи:
1
2
В тетраэдре АВCМ ребро МА
перпендикулярно АВ и АС.
АН – высота треугольника АВС.
ВС=10, АМ=8, АН=6.
Найдите площадь грани МВС.
Определите вид
треугольника А1DC
М
8
А
В
6
Н
С
10

8.

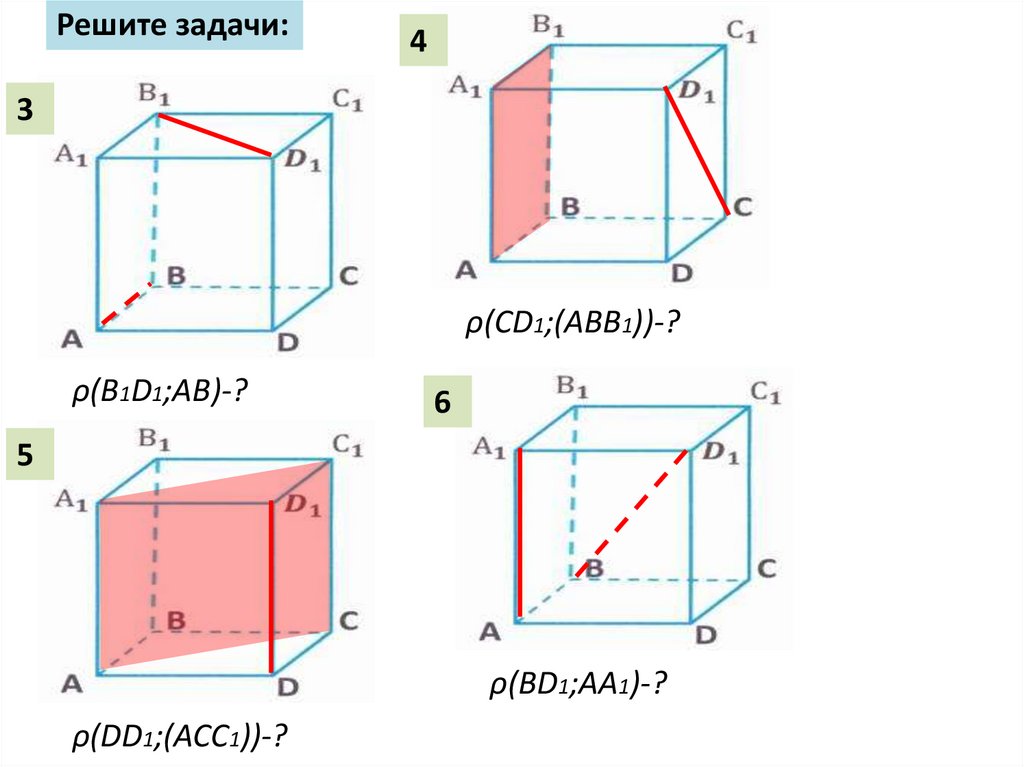
Решите задачи:
4
3
ρ(СD1;(ABВ1))-?
ρ(B1D1;AB)-?
6
5
ρ(BD1;AA1)-?
ρ(DD1;(ACC1))-?

9.

7
8
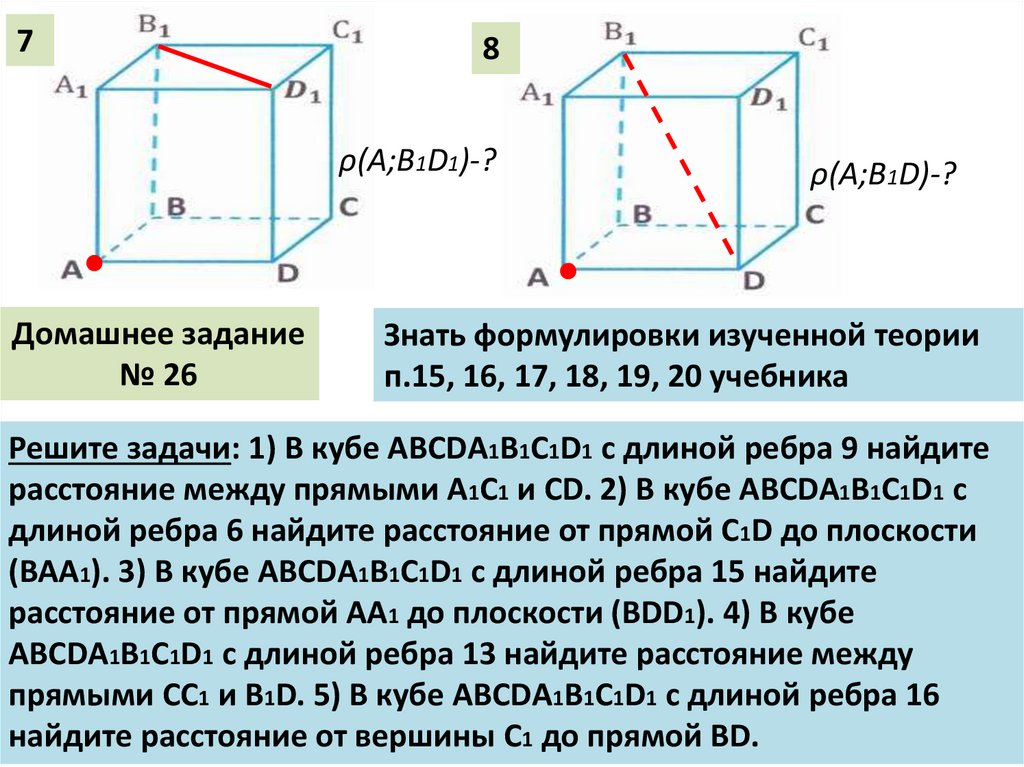
ρ(A;B1D1)-?
Домашнее задание
№ 26
ρ(A;B1D)-?
Знать формулировки изученной теории
п.15, 16, 17, 18, 19, 20 учебника
Решите задачи: 1) В кубе АВСDА1В1С1D1 c длиной ребра 9 найдите
расстояние между прямыми А1С1 и CD. 2) В кубе АВСDА1В1С1D1 c
длиной ребра 6 найдите расстояние от прямой C1D до плоскости
(ВАА1). 3) В кубе АВСDА1В1С1D1 c длиной ребра 15 найдите
расстояние от прямой АА1 до плоскости (ВDD1). 4) В кубе
АВСDА1В1С1D1 c длиной ребра 13 найдите расстояние между
прямыми СС1 и B1D. 5) В кубе АВСDА1В1С1D1 c длиной ребра 16
найдите расстояние от вершины С1 до прямой BD.