bcb0a94aad99458895c91c82dde8427b

1. Симметрия в пространстве

2.

Симметрия, как бы широко или
узко мы ни понимали это слово,
есть идея, с помощью которой
человек веками пытался
объяснить и создать порядок,
красоту и совершенство.
Герман Вейль.

3.

Симметрия –
свойство формы
или расположения
фигур. Происходит
от греческого
«Symmetria» соразмерность,
полное
соответствие в
расположении
частей целого
относительно
средней линии,
центра

4.

История симметрии
Однако как люди дошли до такой сложной и
одновременно такой простой вещи, как симметрия?
Ещё древние греки считали, что симметрия – это
гармония, соразмерность. Они же и ввели термин
συμμετρία, который сейчас перешёл в русское слово
«симметрия»
А у древних народов, таких как шумеры и египтяне, у
первобытных племён, да и у кое-кого в наше время
симметрия ассоциируется не только с красотой и
гармонией, но и прежде всего с магией. Не зря же
люди в эпоху мегалита для ритуальных целей
сооружали кромлихи в форме круга – «идеально
симметричной» геометрической фигуры.

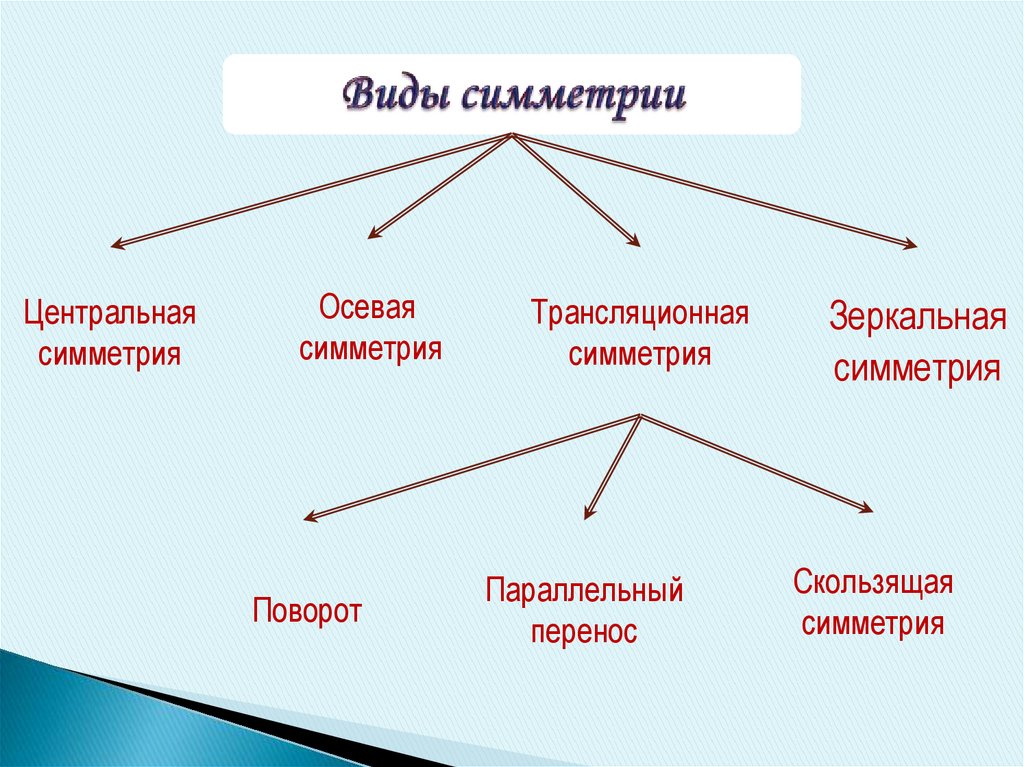
5.

Центральная
симметрия
Осевая
симметрия
Поворот
Трансляционная
симметрия
Параллельный
перенос
Зеркальная
симметрия
Скользящая
симметрия

6.

Точки А и А1 называются
симметричными
относительно прямой (ось
симметрии), если прямая
проходит через середину
отрезка АА1
и
перпендикулярна этому
отрезку. Каждая точка
прямой а считается
симметричной самой себе.
Лист, бабочка – примеры
осевой симметрии.
а
А

7.

Точки А и А1 называются
симметричными относительно
плоскости (плоскость
симметрии), если эта
плоскость проходит через
середину отрезка АА1
и
перпендикулярна этому
отрезку. Каждая точка
плоскости считается
симметричной самой себе.
А
А1

8.

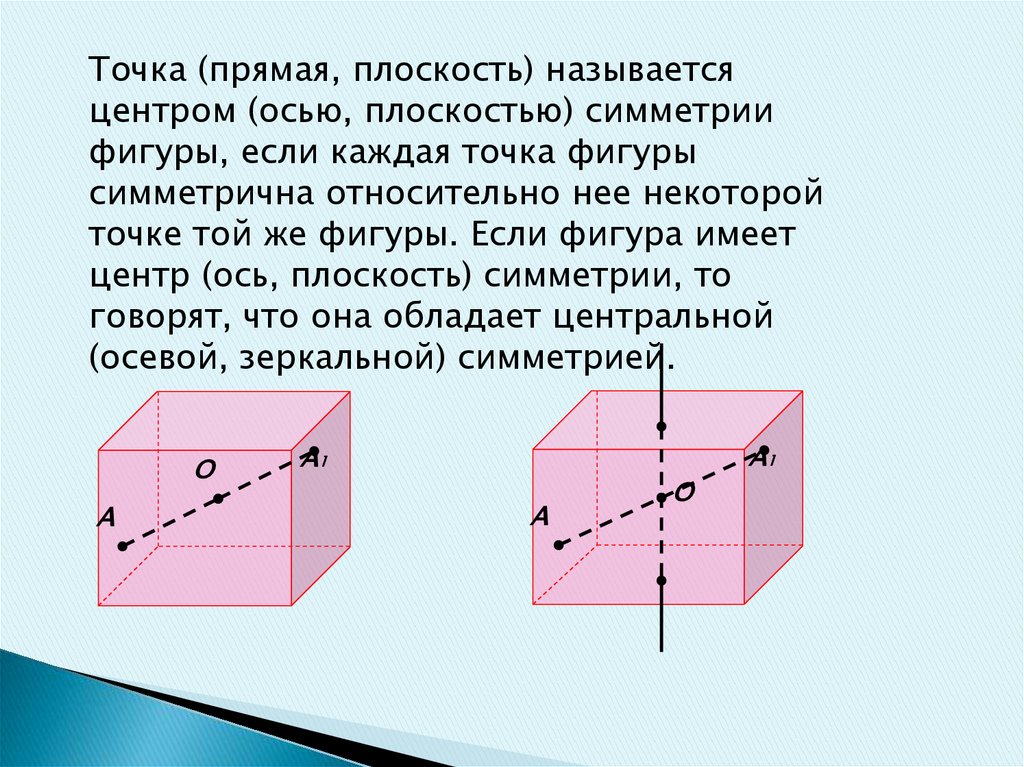
Точка (прямая, плоскость) называется
центром (осью, плоскостью) симметрии
фигуры, если каждая точка фигуры
симметрична относительно нее некоторой
точке той же фигуры. Если фигура имеет
центр (ось, плоскость) симметрии, то
говорят, что она обладает центральной
(осевой, зеркальной) симметрией.
О
А
А1
А1
А
О

9.

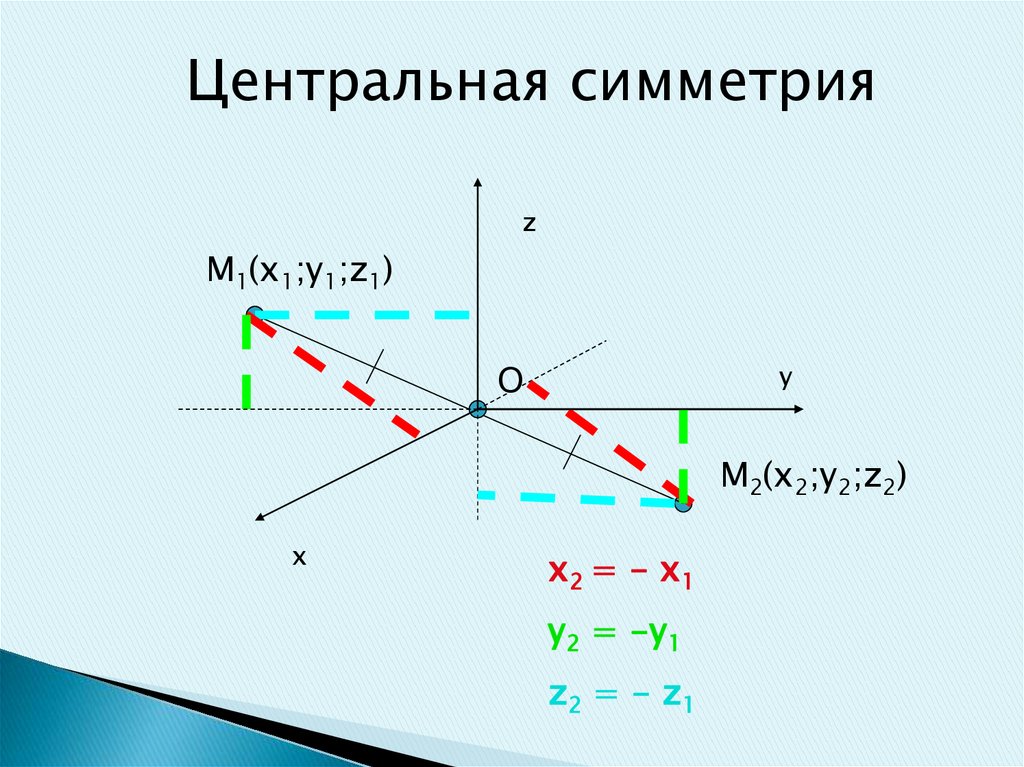
Центральная симметрия
z
М1(х1;y1;z1)
О
y
М2(х2;y2;z2)
x
x2 = - x1
y2 = -y1
z2 = - z1

10.

Осевая симметрия
z
М1 (х1;y1;z1)
l
y
М2(х2;y2;z2)
x
x2 = - x1
y2 = - y1
z2 = z1

11.

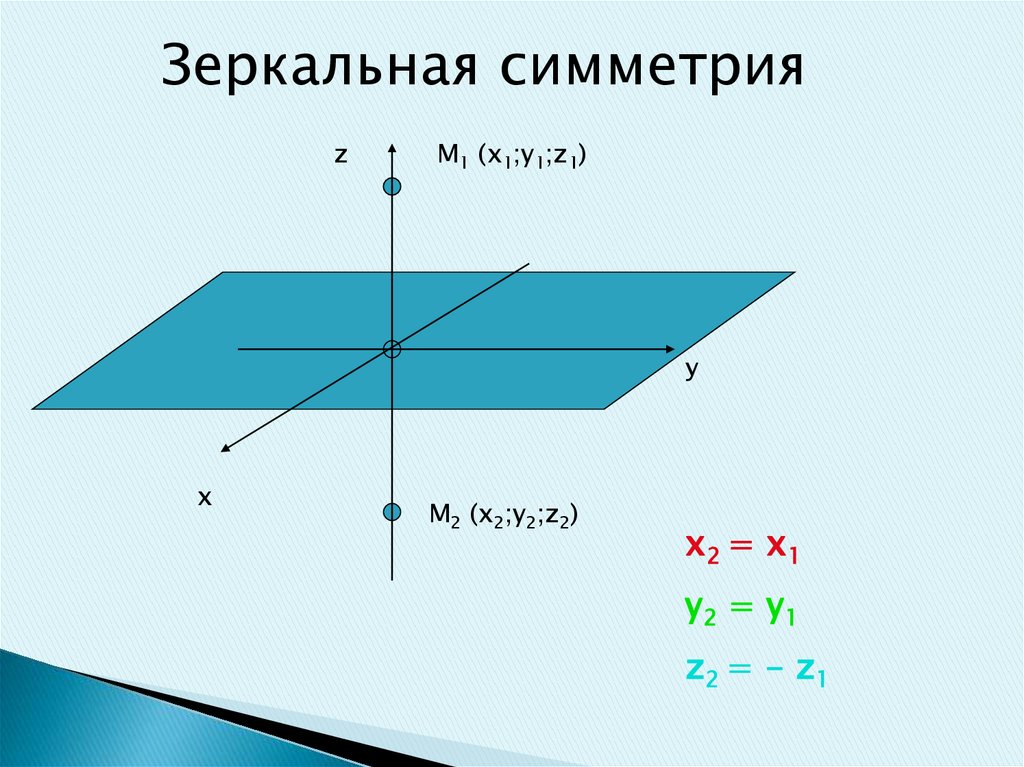
Зеркальная симметрия
z
M1 (x1;y1;z1)
у
х
M2 (x2;y2;z2)
x2 = x1
y2 = y1
z2 = - z1

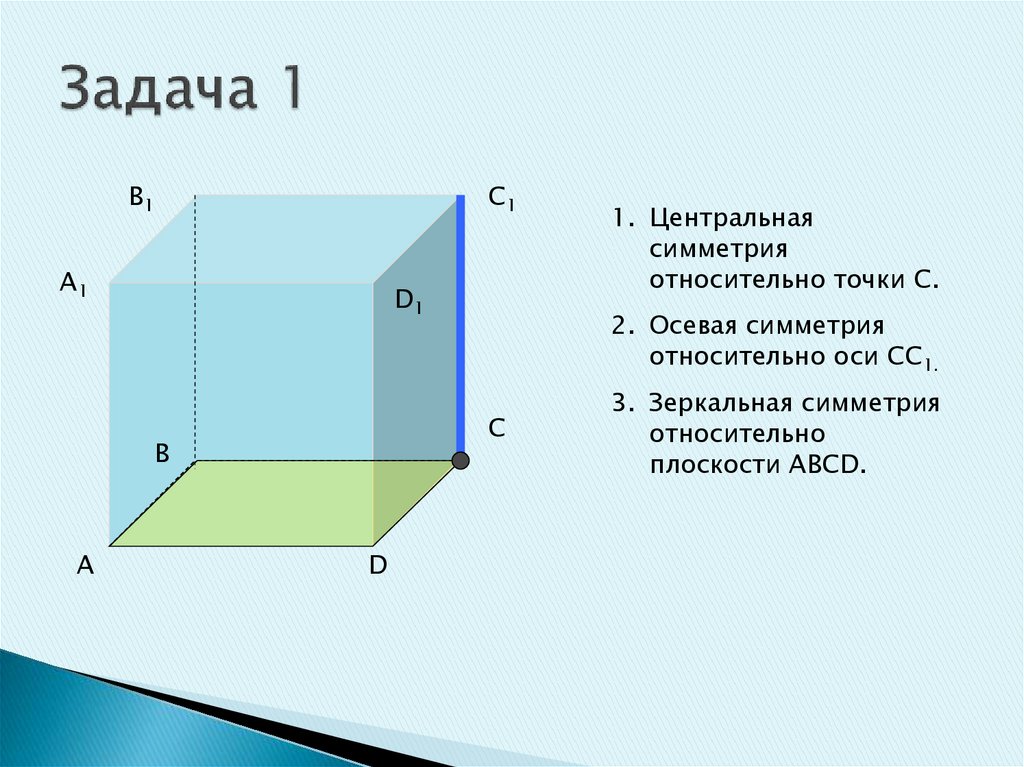
12. Задача 1

В1
С1
А1
D1
А
2. Осевая симметрия
относительно оси СС1.
С
В
D
1. Центральная
симметрия
относительно точки С.
3. Зеркальная симметрия
относительно
плоскости АВСD.

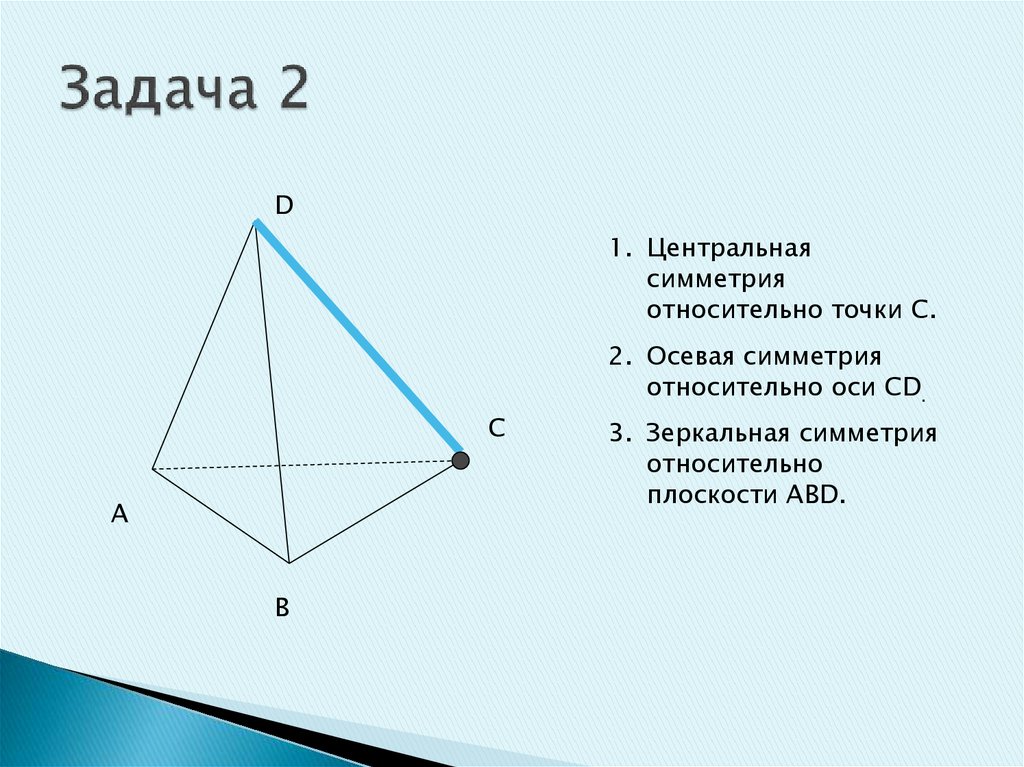
13. Задача 2

D
1. Центральная
симметрия
относительно точки С.
2. Осевая симметрия
относительно оси СD.
С
А
В
3. Зеркальная симметрия
относительно
плоскости АВD.