симплекс-метод

1. СИМПЛЕКС-МЕТОД

2.

Симплекс-метод позволяет решать задачи
линейного программирования любой
размерности, т.е. с любым количеством
переменных.

3. Основные этапы симплекс-метода

1 этап. Задача линейного программирования приводится к
канонической форме.
L X c1 x1 c2 x2 ... cn xn max
a11 x1 a12 x2 ... a1n xn b1 ,
a21 x1 a22 x2 ... a2 n xn b2 ,
. ..
a x a x ... a x b ,
m2 2
mn n
m
m1 1
x1 , x2 ,..., xn 0.
Примечание. Ограничение-неравенство исходной задачи ЛП, имеющее вид
« ≤ » можно преобразовать в ограничение-равенство добавлением к его
левой части дополнительной неотрицательной переменной, а ограничение
Неравенство вида « ≥ » – в ограничение-равенство вычитанием из его
левой части дополнительной неотрицательной переменной.
ai1x1 ai 2 x2 ... ain xn bi ai1x1 ai 2 x2 ... ain xn xn 1 bi
ai1x1 ai 2 x2 ... ain xn bi ai1x1 ai 2 x2 ... ain xn xn 1 bi

4.

2 этап Определяется начальное допустимое
решение.
Для определения начального решения выделяются базисные и
небазисные (свободные) переменные.
В качестве базисных принимаются переменные, входящие в
ограничение с коэффициентом, равным единице, и при этом не
входящая ни в одно из других ограничений или остаточные
переменные, введенные при приведении задачи к канонической
форме. Базисные переменные принимают значения, равные
правым частям ограничений. Все остальные (небазисные)
переменные принимаются равными нулю.
Целевая функция выражается через свободные переменные.

5.

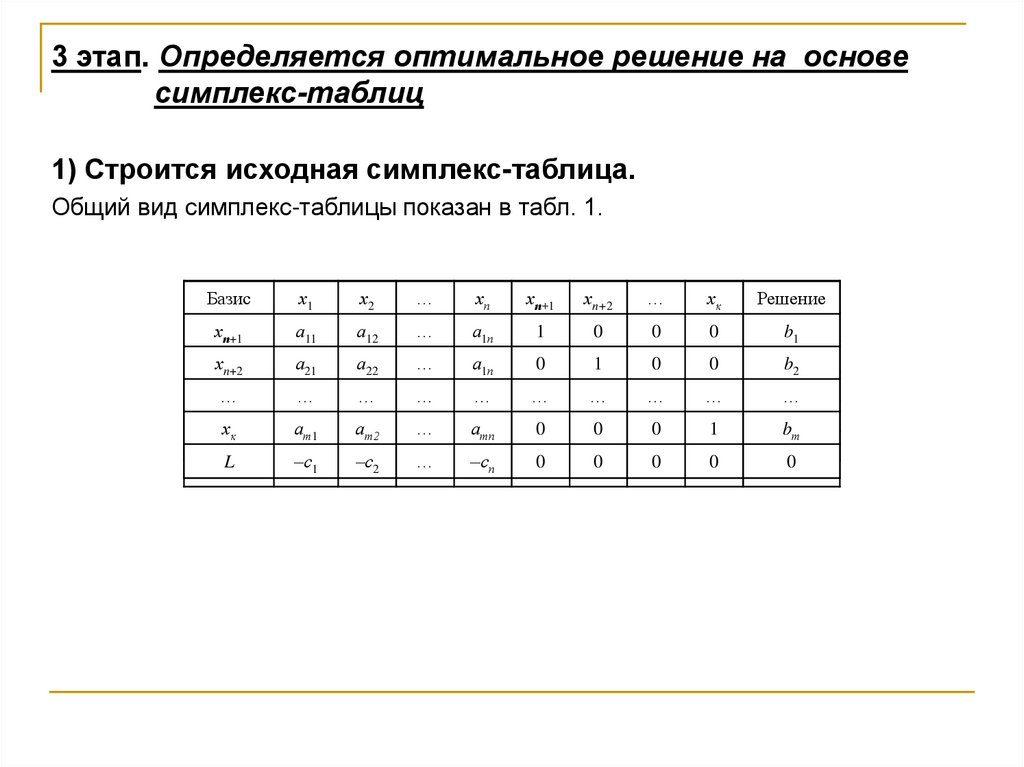
3 этап. Определяется оптимальное решение на основе
симплекс-таблиц
1) Строится исходная симплекс-таблица.
Общий вид симплекс-таблицы показан в табл. 1.
Базис
Базис
х11
х22
…
…
хпп
ххп+1
п+1
ххn+2
n+2
…
…
хкк
Решение
Решение
п+1
ххп+1
аа11
11
аа12
12
…
…
…
аа1п
1п
11
00
00
00
bb11
n+2
ххn+2
аа21
21
22
аа22
…
…
…
1п
аа1п
00
11
00
00
bb22
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
х
…
…
…
а
…
…
…
а
…
…
…
…
хкк
ат1
т1
т2
ат2
…
…
L
–с1
–с2
…
…
L
–с1
–с2
…
…
…
…
а
…
…
0
тп
атп
0
–сп
0
–сп
0
0
0
0
0
0
0
0
0
1
1
0
0
…
b
bтт
0
0

6.

Симплекс-таблица строится по следующим правилам:
в первой строке перечисляются все переменные задачи, как
исходные (х1, х2,..., хn), так и дополнительные, введенные при
приведении к канонической форме (хn+1, хn+2,..., хk).
в первой колонке таблицы («Базис») перечисляются базисные
переменные. Их количество всегда равно количеству ограничений.
в строке целевой функции указываются коэффициенты целевой
функции с обратным знаком.
в строках базисных переменных указываются коэффициенты
ограничений, в которые входят эти переменные. Для переменных, не
входящих в ограничения, указываются нулевые коэффициенты;
в последнем столбце («Решение») указываются значения базисных
переменных (они равны правым частям ограничений), а также
начальное значение целевой функции (0).
Если таблица построена правильно, то в столбце каждой базисной
переменной должна присутствовать только одна единица (в строке
ограничения, в которое входит эта переменная); остальные
коэффициенты – нулевые.

7.

2) Проверяется условие окончания решения задачи. Если в строке
целевой функции (L-строке) все коэффициенты неотрицательны,
это означает, что оптимальное решение найдено. В противном
случае выполняется следующий шаг.
3) Определяется переменная для включения в базис. В качестве такой
переменной выбирается переменная, которой соответствует
максимальный по модулю отрицательный коэффициент в Lстроке. Включение в базис (т.е. увеличение) такой переменной
приводит к наиболее быстрому росту целевой функции. Столбец
переменной, выбранной для включения в базис, называется
ведущим (разрешающим).
Примечание. Если в L-строке имеется несколько максимальных по
модулю отрицательных элементов (равных между собой), то для
включения в базис можно выбирать любую из соответствующих
переменных.

8.

4) Определяется переменная для исключения из базиса. Для этого
вычисляются отношения значений базисных переменных
(указанных в столбце «Решение») к соответствующим элементам
ведущего столбца. Такие отношения (называемые симплексными
отношениями) вычисляются только для положительных
коэффициентов ведущего столбца. Переменная, которой
соответствует минимальное симплексное отношение, исключается
из базиса.
Строка переменной, выбранной для исключения из базиса,
называется ведущей (разрешающей). Элемент на пересечении
ведущей строки и столбца называется ведущим (разрешающим)
элементом.
Примечания:
Если имеется несколько минимальных симплексных отношений
(равных между собой), то для исключения из базиса можно
выбирать любую из соответствующих переменных.
Если все элементы ведущего столбца оказываются отрицательными
или равными нулю (т.е. невозможно вычислить ни одного
симплексного отношения), это означает, что допущена ошибка в
постановке задачи или в математической модели (не учтено
некоторое ограничение).

9.

5) Выполняется преобразование симплекс-таблицы по следующим правилам:
в столбце «Базис» вместо переменной, исключенной из базиса на шаге 4,
указывается переменная, включенная в базис на шаге 3;
все элементы ведущей строки делятся на ведущий элемент;
все элементы ведущего столбца (кроме ведущего элемента) заменяются
нулями;
все остальные элементы таблицы (включая L-строку и столбец «Решение»)
пересчитываются по «правилу прямоугольника». Этот пересчет
выполняется следующим образом: ведущий и пересчитываемый элемент
образуют диагональ прямоугольника; находится произведение ведущего и
пересчитываемого прямоугольника; из этого произведения вычитается
произведение элементов, образующих противоположную диагональ
прямоугольника; результат делится на ведущий элемент.
6) Выполняется возврат к шагу 2.
По окончании алгоритма в столбце «Решение» находятся оптимальные
значения базисных переменных, а также значение целевой функции,
соответствующее полученному решению. Оптимальные значения
небазисных переменных равны нулю.