Лебедева_А. презентация (1)

1.

Министерство лесного хозяйства Владимирской области
ГБПОУ ВО «Муромцевский леотехнический техникум»
Загадка простых чисел
Автор работы:
студентка 1 курса
группы 14 ТЭО
очной формы обучения
А.А. Лебедева
Проверил:
преподаватель
О. В. Дымова
п. Муромцево 2025

2.

Введение
Простые числа занимают центральное место в теории чисел,так как любое
натуральное число может быть единственным образом, представленном в виде
произведения протых множителей. Они важны в разных областях, включая
математику, криптографию и т.д.

3.

Изучение основных теоретических положений, касающихся
простых чисел.
Простые числа — это натуральные числа больше 1, которые делятся только на
1 и на самого себя. Они занимают фундаментальное место в теории чисел и
являются своего рода «строительными блоками» для всех натуральных
чисел, поскольку каждое число можно разделить на произведение простых
множителей.

4.

Над математической формулой
поиска простых чисел математики
бьются последние 3,5 тысячи лет.
Пока ее не нашли. Но зато
составили таблицу простых чисел,
которая помогает эти числа
упорядочить. Принцип, по
которому простые числа попадают
в таблицу, придумал еще
древнегреческий ученый
Эратосфен.
Именно он, вычеркивая числа, кратные 2, 3 и далее по очереди, создал таблицу первой
тысячи натуральных чисел. Таблица простых чисел помогает в решении основной теоремы
арифметики. По ней все натуральные числа являются простыми либо раскладываются на
простые множители. Исключение — 1. В поисках множителей конкретного числа следует
заглянуть в таблицу простых чисел. Если это число в ней представлено — значит, оно является
простым. Если нет — нужно найти все делители.

5.

Поиск простых чисел является самой парадоксальной
проблемой математики
Ученые до сих пор пытаются решить их загадку
Открытие П.Л. Чебышева
В 1850 г. он доказал, что между любым натуральным числом (не
равным 1) и числом, в два раза больше его,находится хотя бы одно
простое число.
Чебышев использовал метод доказательства теорем,
касающихся бесконечных последовательных чисел. Суть метода в
том, чтобы доказать утверждение для всех чисел больше
определённого значения, при этом значение должно быть таким,
чтобы все меньшие числа можно было проверить перебором.
В этом случае Чебышев с помощью тета-функции (сумма
логарифмов простых чисел, не превосходящих данное число)
обосновал постулат Бертрана для чисел, больших 160, чего уже
было достаточно для оформления доказательства.

6.

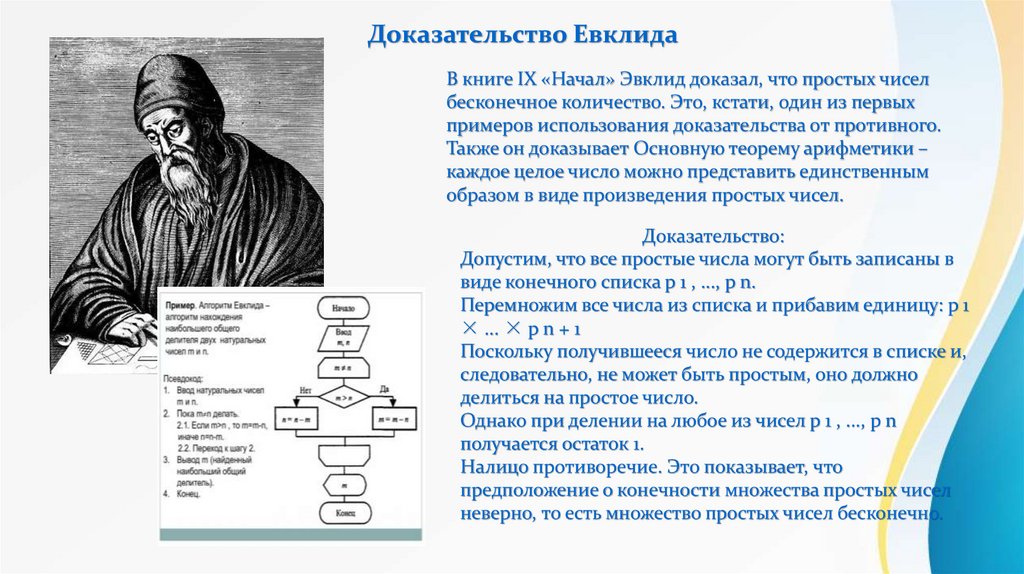
Доказательство Евклида
В книге IX «Начал» Эвклид доказал, что простых чисел
бесконечное количество. Это, кстати, один из первых
примеров использования доказательства от противного.
Также он доказывает Основную теорему арифметики –
каждое целое число можно представить единственным
образом в виде произведения простых чисел.
Доказательство:
Допустим, что все простые числа могут быть записаны в
виде конечного списка p 1 , ..., p n.
Перемножим все числа из списка и прибавим единицу: p 1
× ... × p n + 1
Поскольку получившееся число не содержится в списке и,
следовательно, не может быть простым, оно должно
делиться на простое число.
Однако при делении на любое из чисел p 1 , ..., p n
получается остаток 1.
Налицо противоречие. Это показывает, что
предположение о конечности множества простых чисел
неверно, то есть множество простых чисел бесконечно.

7.

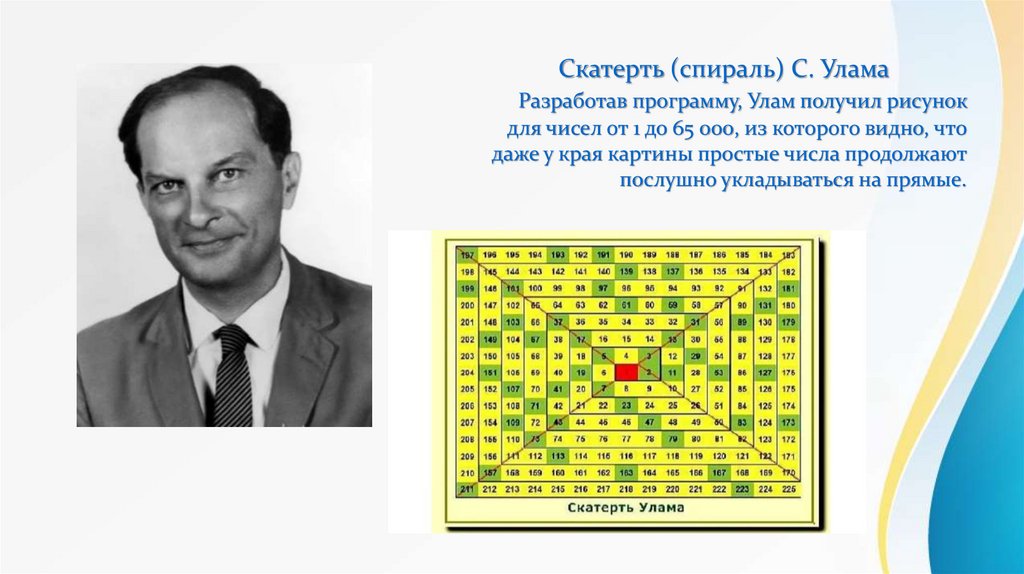
Скатерть (спираль) С. Улама
Разработав программу, Улам получил рисунок
для чисел от 1 до 65 000, из которого видно, что
даже у края картины простые числа продолжают
послушно укладываться на прямые.

8.

Задание 1. «Тайна Простых чисел:
Создаем Скатерть Улама!»

9.

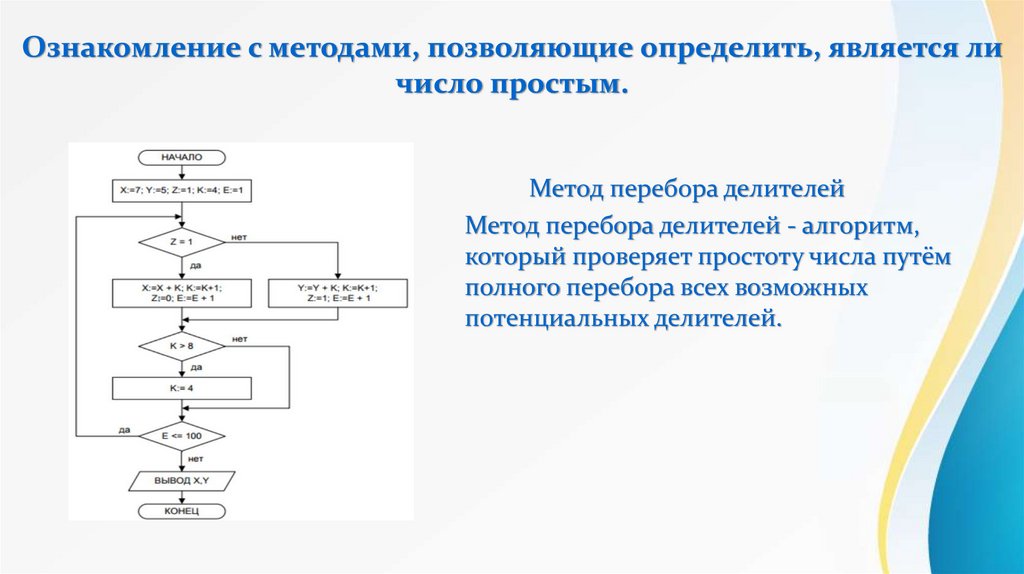
Ознакомление с методами, позволяющие определить, является ли
число простым.
Метод перебора делителей
Метод перебора делителей - алгоритм,
который проверяет простоту числа путём
полного перебора всех возможных
потенциальных делителей.

10.

Задание 2. «Детективы Чисел: Поиск
Тайных делителей!»

11.

Метод Решето Эратосфена
Решето Эратосфена — это алгоритм нахождения
всех простых чисел до заданного натурального
числа путём постепенного отсеивания составных
чисел. Образно говоря, через решето Эратосфена
в процессе его тряски проскакивают составные
числа, а простые остаются в решете.

12.

Задание 3. «Решето Эратосфена:
Фильтр Прайм-Детектива!»

13.

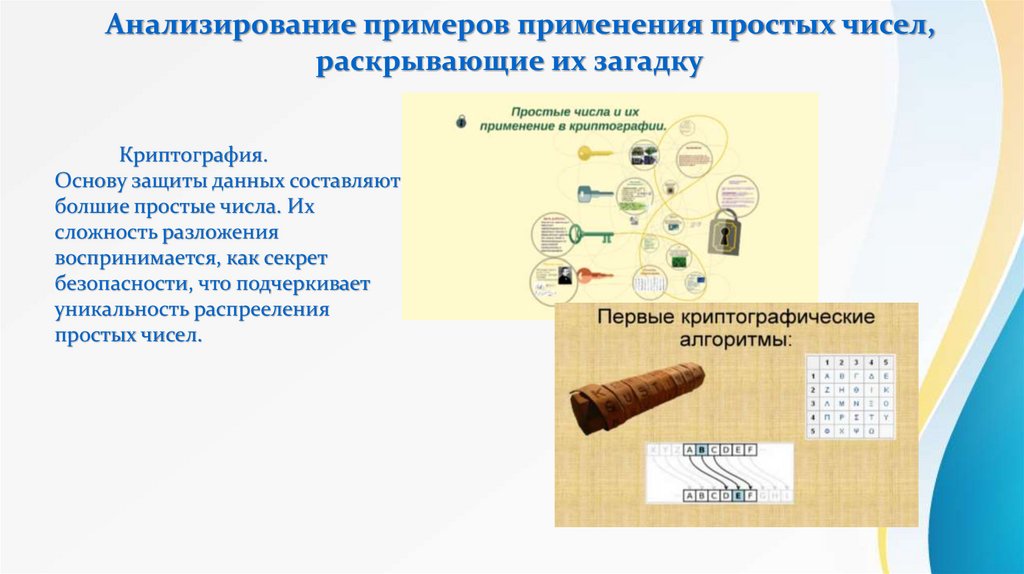
Анализирование примеров применения простых чисел,
раскрывающие их загадку
Криптография.
Основу защиты данных составляют
болшие простые числа. Их
сложность разложения
воспринимается, как секрет
безопасности, что подчеркивает
уникальность распрееления
простых чисел.

14.

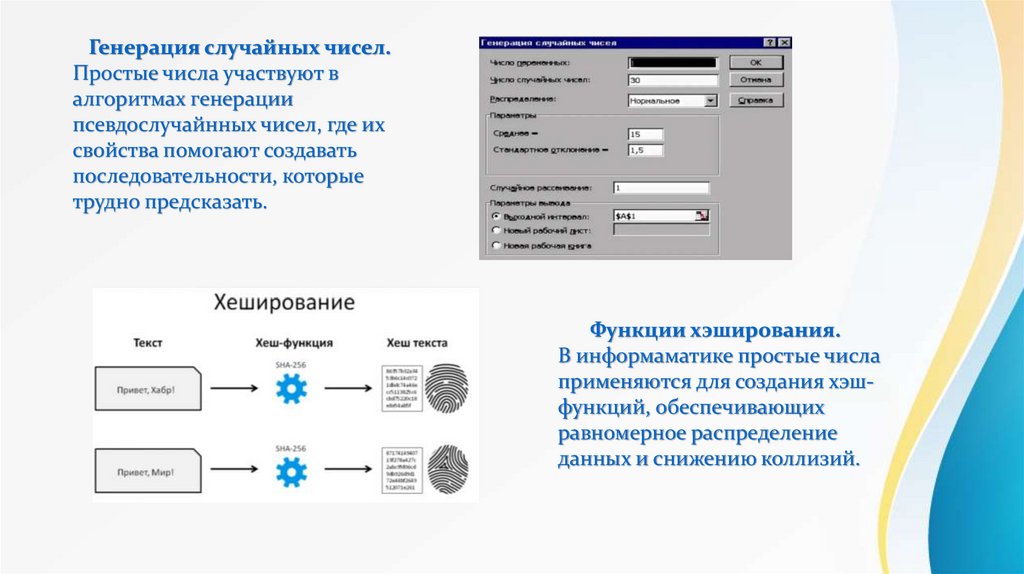
Генерация случайных чисел.
Простые числа участвуют в
алгоритмах генерации
псевдослучайнных чисел, где их
свойства помогают создавать
последовательности, которые
трудно предсказать.
Функции хэширования.
В информаматике простые числа
применяются для создания хэшфункций, обеспечивающих
равномерное распределение
данных и снижению коллизий.

15.

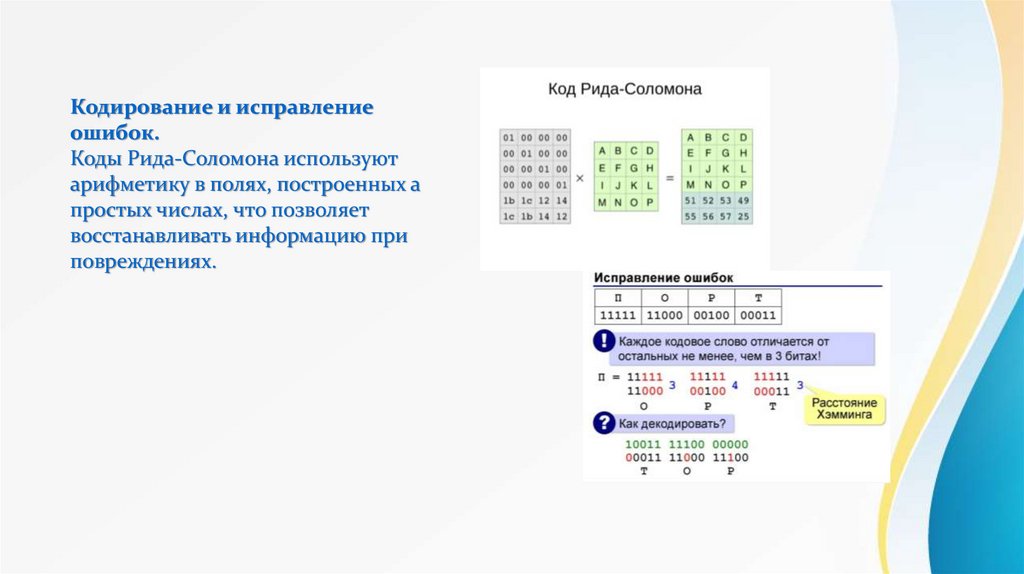
Кодирование и исправление
ошибок.
Коды Рида-Соломона используют
арифметику в полях, построенных а
простых числах, что позволяет
восстанавливать информацию при
повреждениях.

16.

Физика квантовых систем.
Связь распределения простых
чисел с энергетическими уровнями
квантовых систем позволет лучше
понять природу хаоса и порядка.
Фракталы и динамические
системы.
Простые числа участвуют в
построении фрактальных структур,
где они определяют сложные, но
повторяющиеся паттерны.

17.

Заключение
Простые числа играют ключевую роль в теории чисел, так как любое
натуральное число можно представить в виде произведения простых
множителей, и эта разложение является единственным. Их свойства лежат в
основе многих важных областей, таких как криптография, компьютерные
науки и теория алгоритмов. Изучение простых чисел способствует развитию
понимания структуры чисел и помогает решать сложные математические
задачи. Несмотря на кажщуюся простоту, многие вопросы, связанные с
простыми числами, остаются нерешенными и продолжают вдохновлять
математиков по всему миру.