Similar presentations:
Лекция_по_теме_Перпендикулярность_прямых_и_плоскостей_в_пространстве
1.
2.
Вопросы:1. Перпендикулярные прямые в пространстве
2. Признак перпендикулярности прямой и
плоскости
3. Расстояние
от
точки
до
плоскости.
Перпендикуляр. Наклонная
4. Теорема о трех перпендикулярах.
5. Угол между прямой и плоскостью
3.
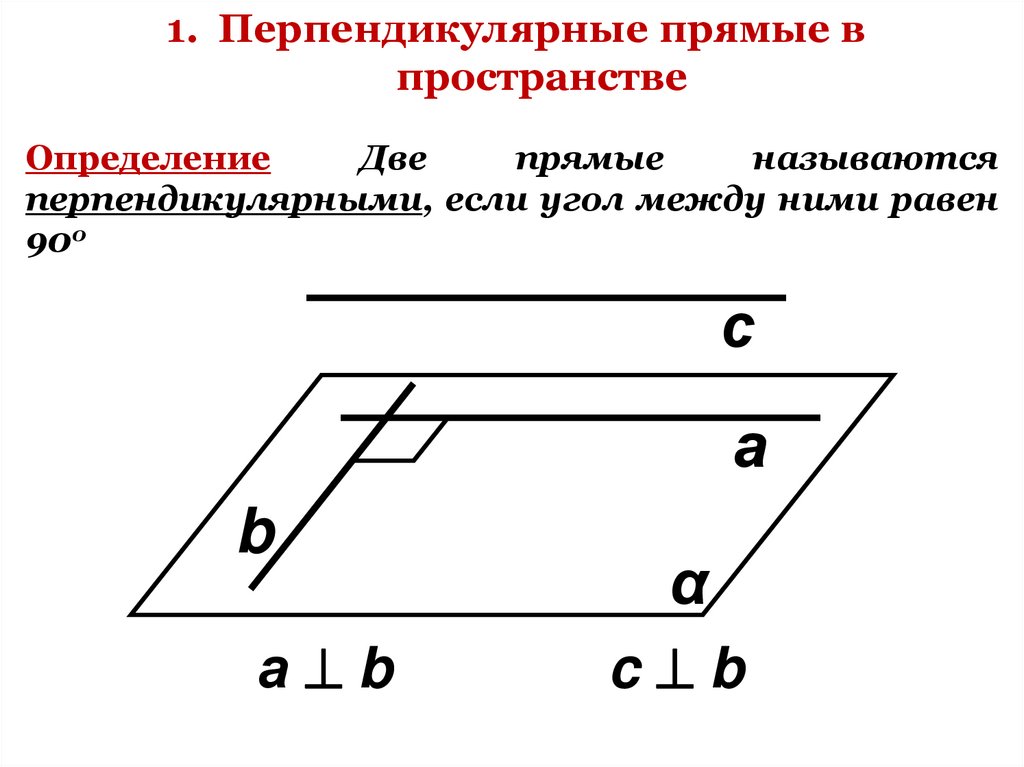
1. Перпендикулярные прямые впространстве
Определение
Две
прямые
называются
перпендикулярными, если угол между ними равен
90о
с
а
b
а b
α
c b
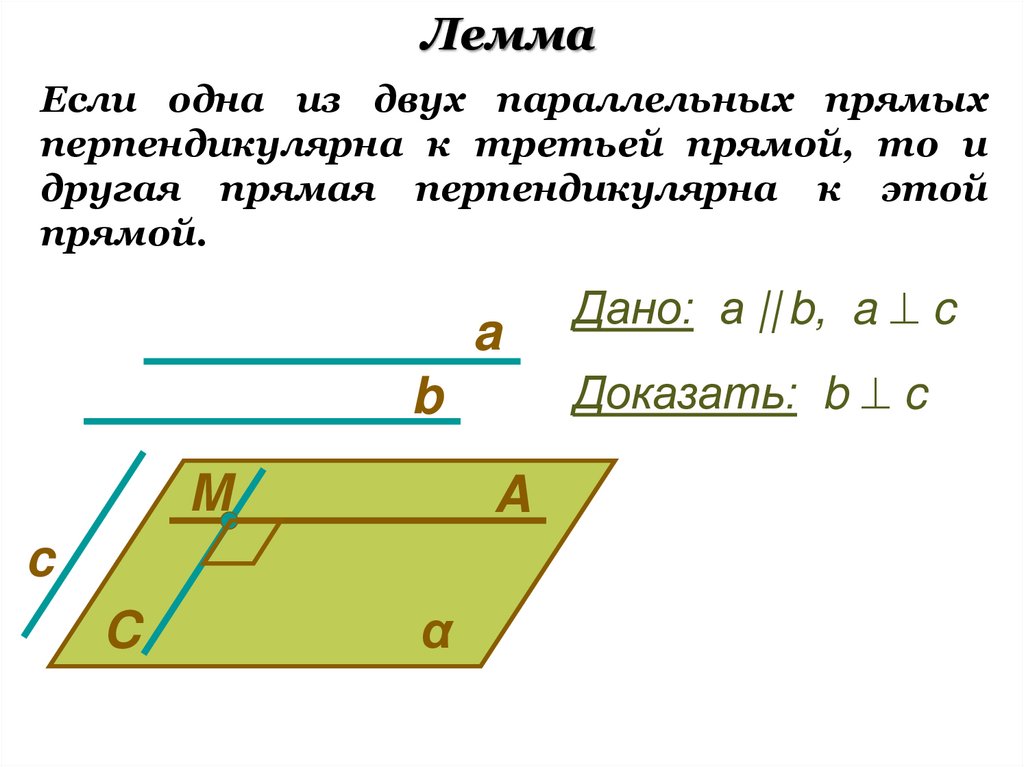
4. Лемма
Если одна из двух параллельных прямыхперпендикулярна к третьей прямой, то и
другая прямая перпендикулярна к этой
прямой.
a
Доказать: b c
b
M
A
c
C
α
Дано: а || b, a c
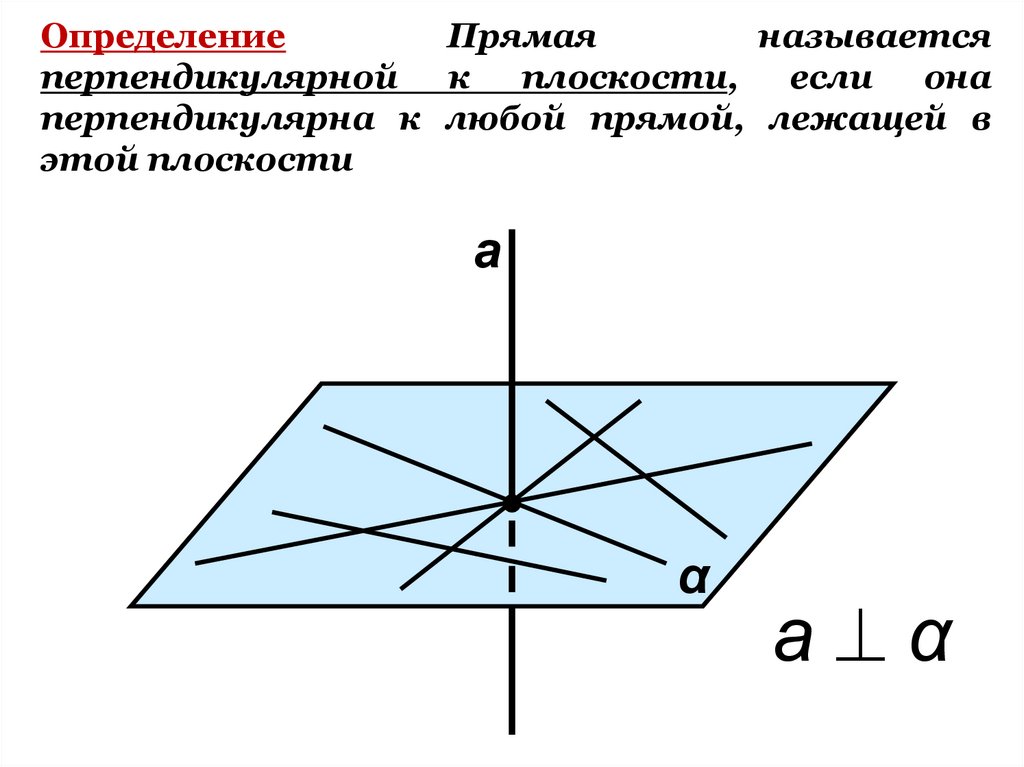
5. Определение Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости
аα
а α
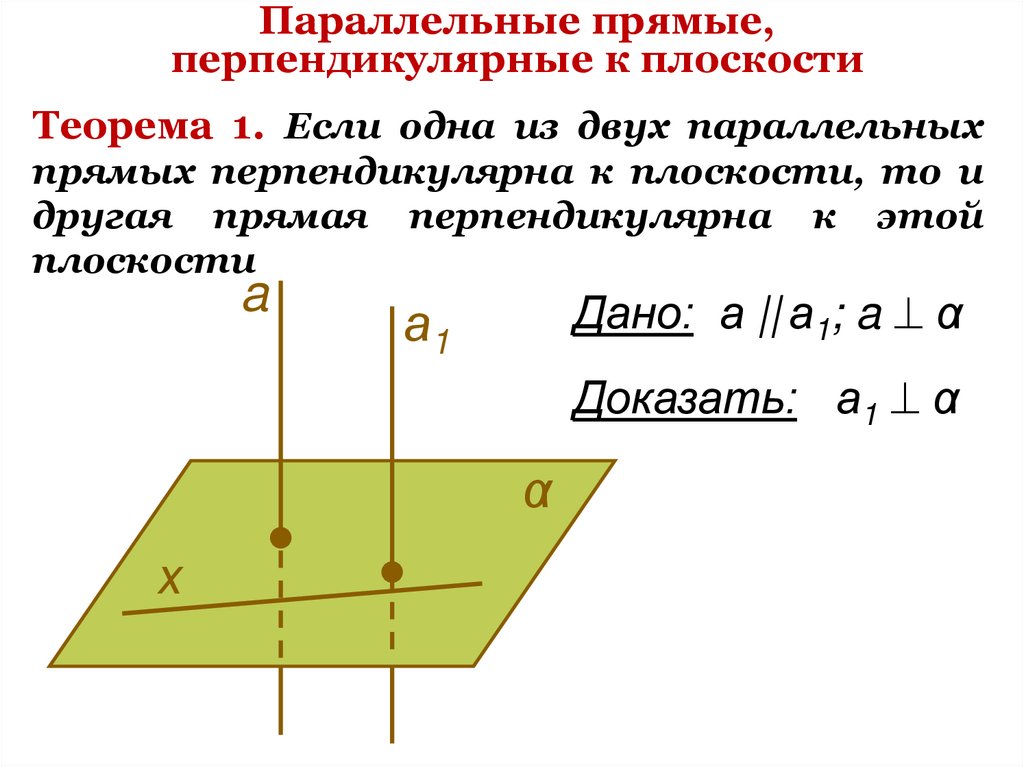
6. Параллельные прямые, перпендикулярные к плоскости
Теорема 1. Если одна из двух параллельныхпрямых перпендикулярна к плоскости, то и
другая прямая перпендикулярна к этой
плоскости
a
Дано: а || а1; a α
а1
Доказать: а1 α
α
х
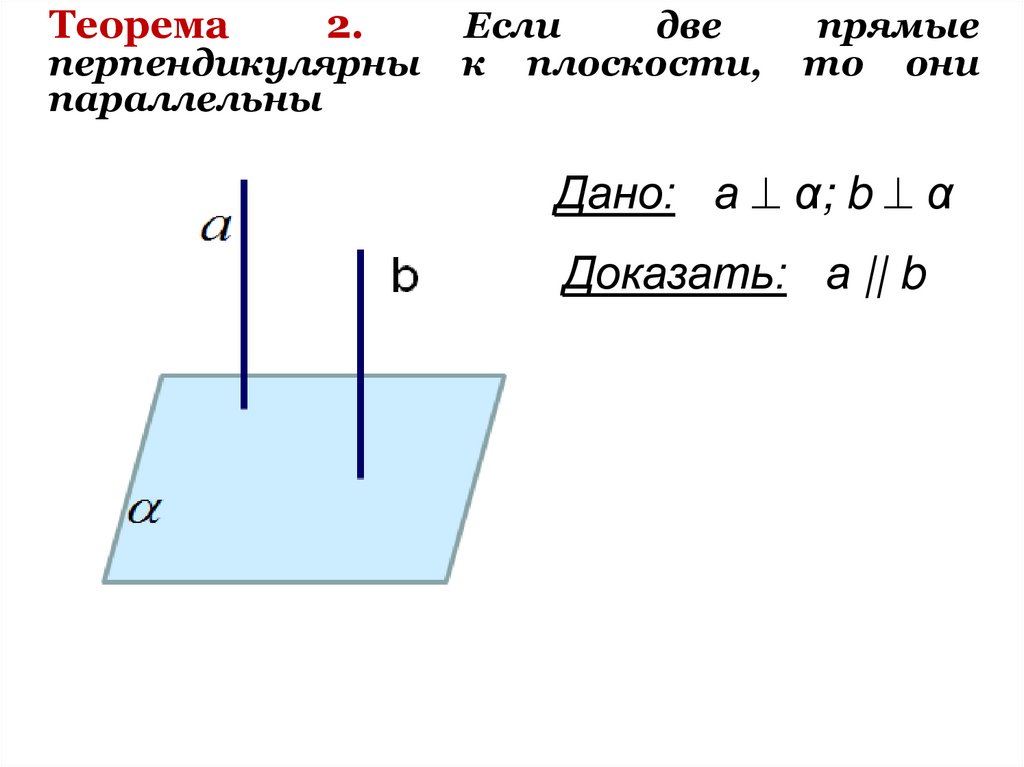
7. Теорема 2. Если две прямые перпендикулярны к плоскости, то они параллельны
Теорема2.
перпендикулярны
параллельны
Если
две
к плоскости,
прямые
то они
Дано: а α; b α
Доказать: а || b
8. 2. Признак перпендикулярности прямой и плоскости
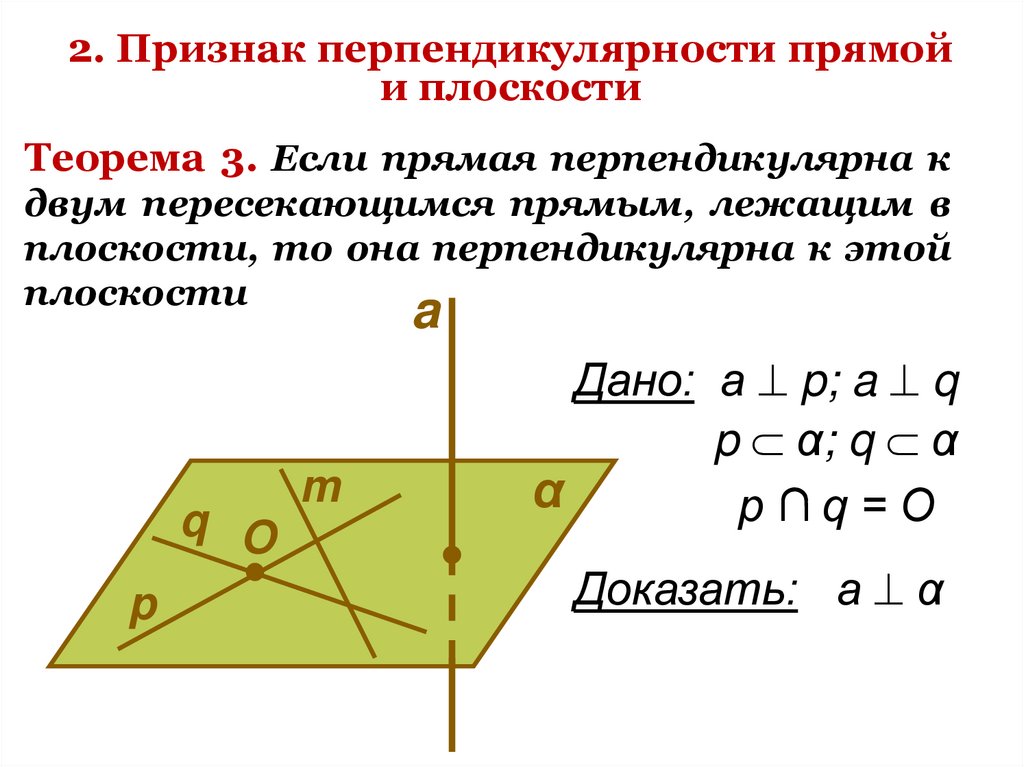
Теорема 3. Если прямая перпендикулярна кдвум пересекающимся прямым, лежащим в
плоскости, то она перпендикулярна к этой
плоскости
a
q O
p
m
Дано: а p; a q
p α; q α
α
p∩q=О
Доказать: а α
9.
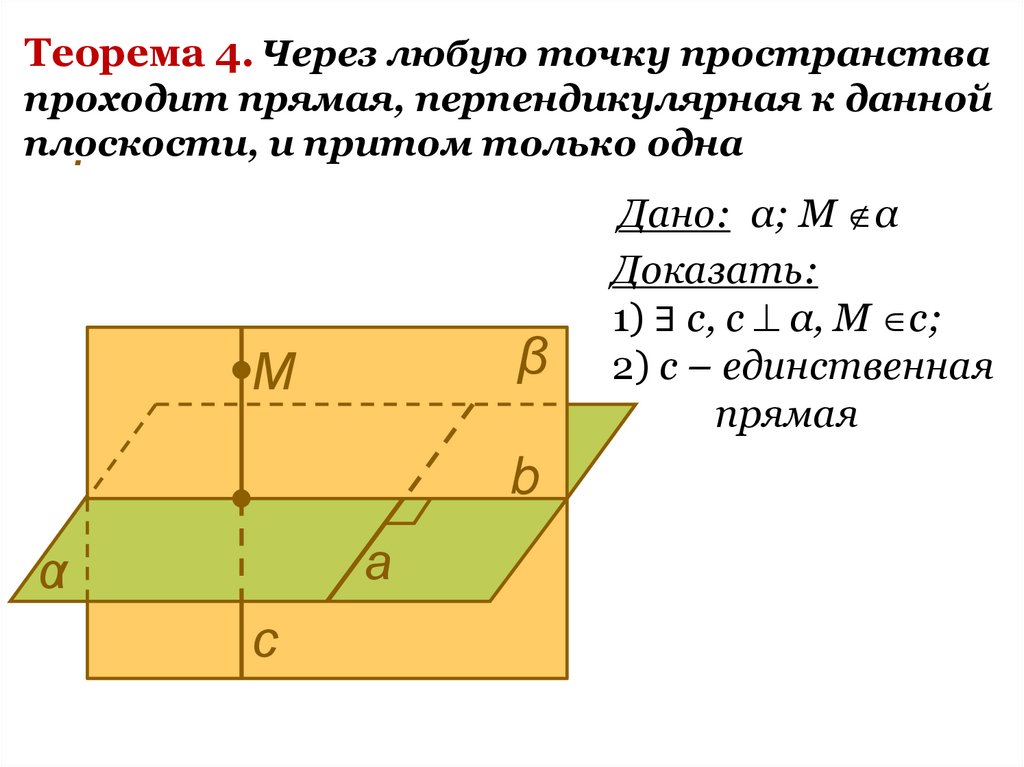
Теорема 4. Через любую точку пространствапроходит прямая, перпендикулярная к данной
плоскости,
и притом только одна
.
β
М
b
а
α
с
Дано: α; М α
Доказать:
1) ∃ с, с α, М с;
2) с – единственная
прямая
10.
2. Признак перпендикулярностипрямой и плоскости
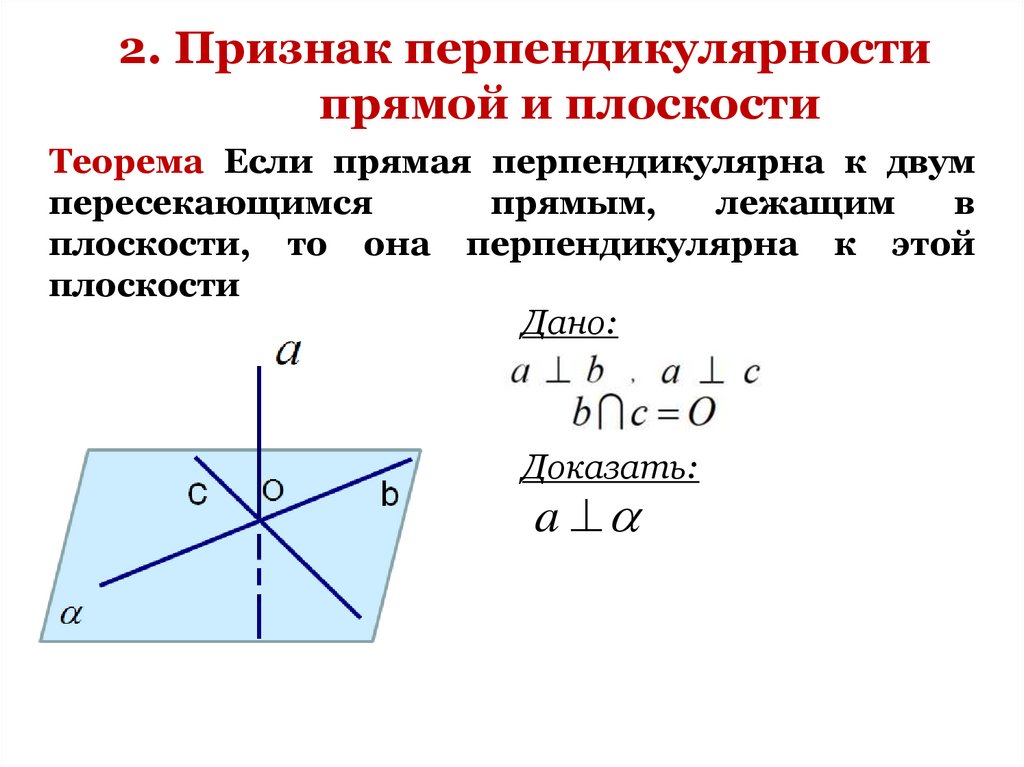
Теорема Если прямая перпендикулярна к двум
пересекающимся
прямым,
лежащим
в
плоскости, то она перпендикулярна к этой
плоскости
Дано:
Доказать:
a
11.
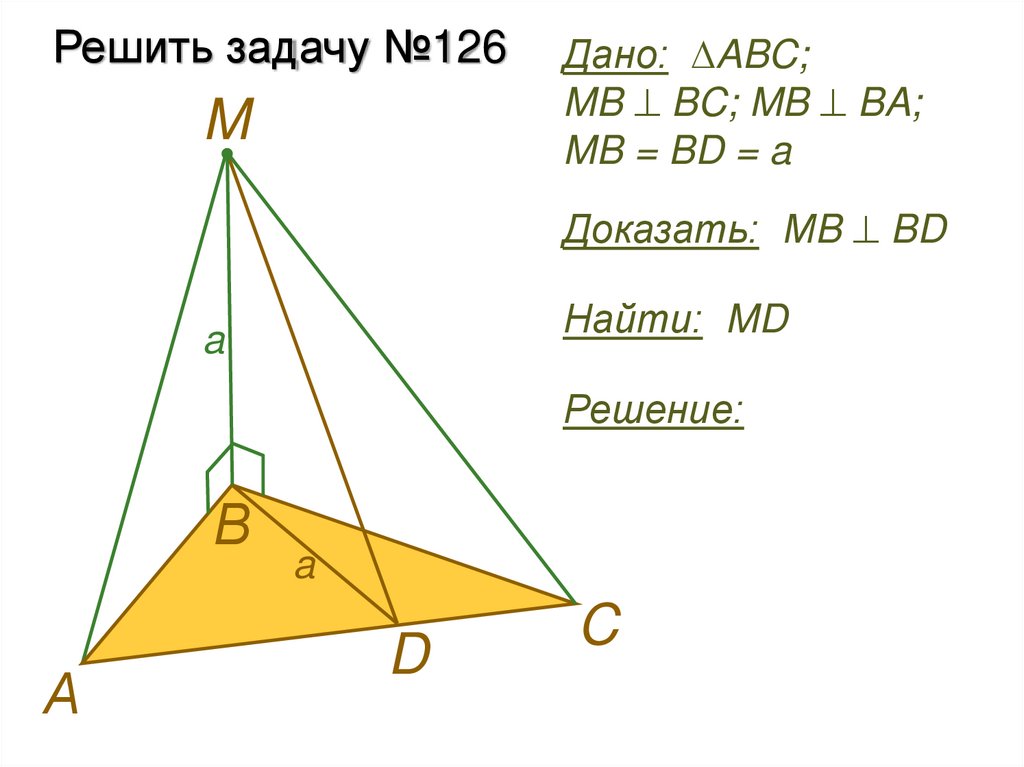
Решить задачу №126M
Дано: ABC;
MB BC; MB BA;
MB = BD = a
Доказать: МB BD
Найти: MD
a
Решение:
В
А
a
D
C
12.
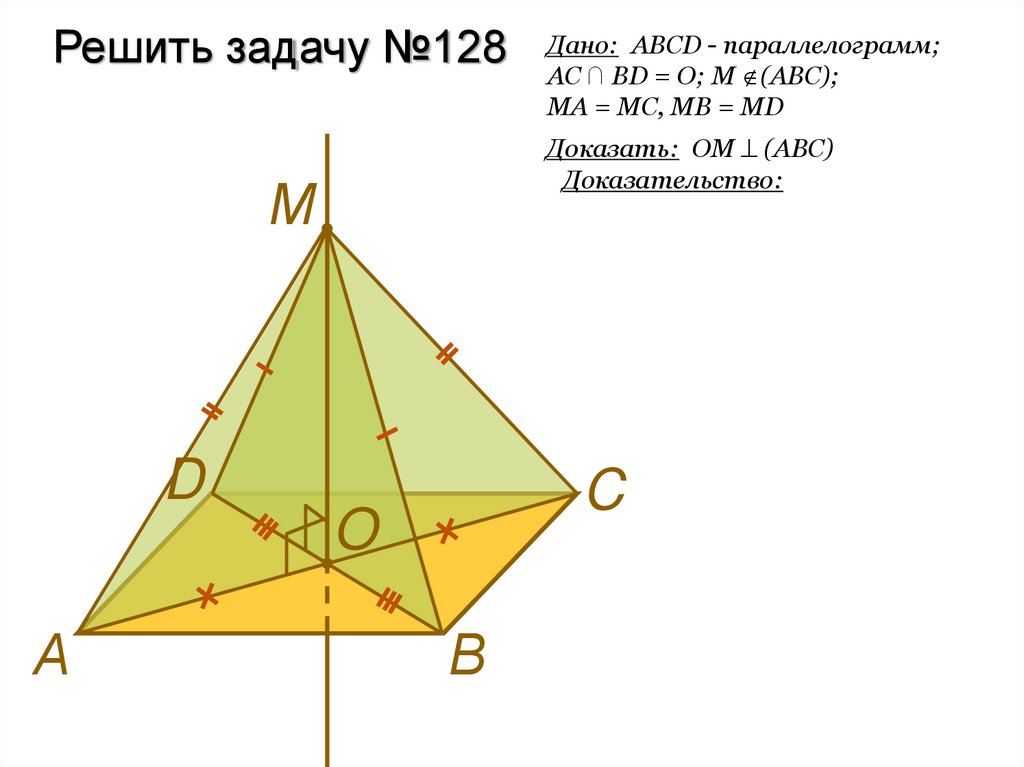
Решить задачу №128Доказать: OМ (ABC)
Доказательство:
М
D
А
Дано: ABCD - параллелограмм;
AC ∩ BD = O; М (ABC);
МА = МС, MB = MD
C
O
В
13.
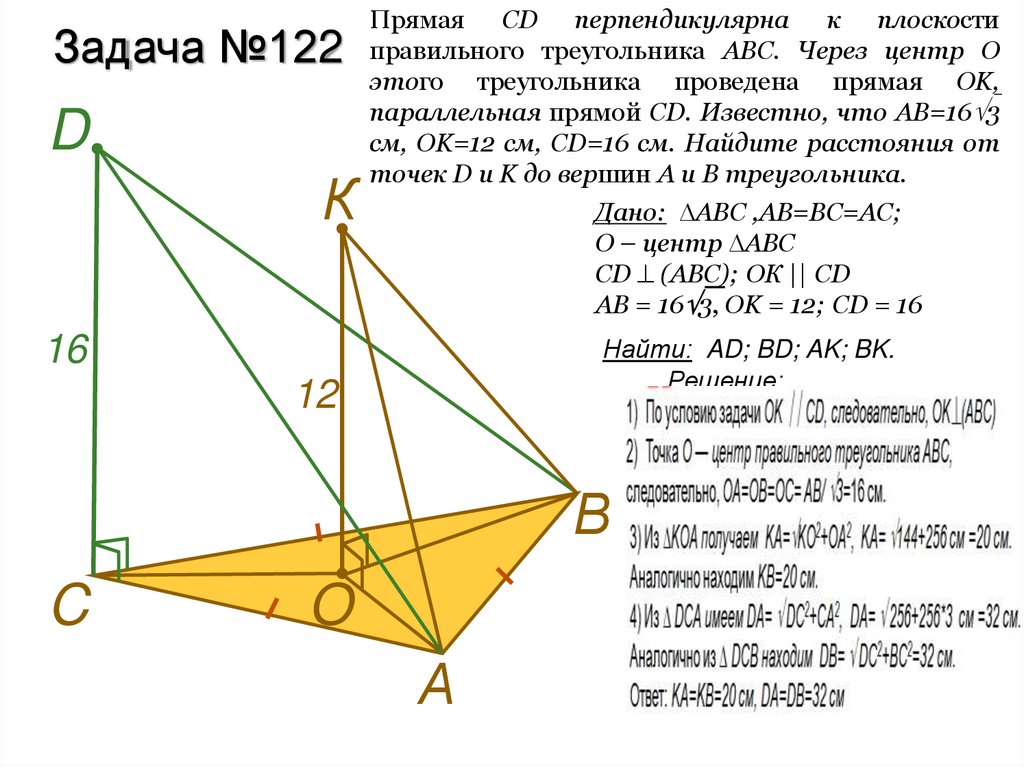
Задача №122D
К
Прямая CD перпендикулярна к плоскости
правильного треугольника ABC. Через центр O
этого треугольника проведена прямая OK,
параллельная прямой CD. Известно, что AB=16 3
см, OK=12 см, CD=16 см. Найдите расстояния от
точек D и K до вершин A и B треугольника.
Дано: ABC ,АВ=ВС=АС;
О – центр ABC
CD (ABC); ОК || CD
АB = 16 3, OK = 12; CD = 16
16
Найти: AD; BD; AK; BK.
Решение:
12
В
C
O
А
14.
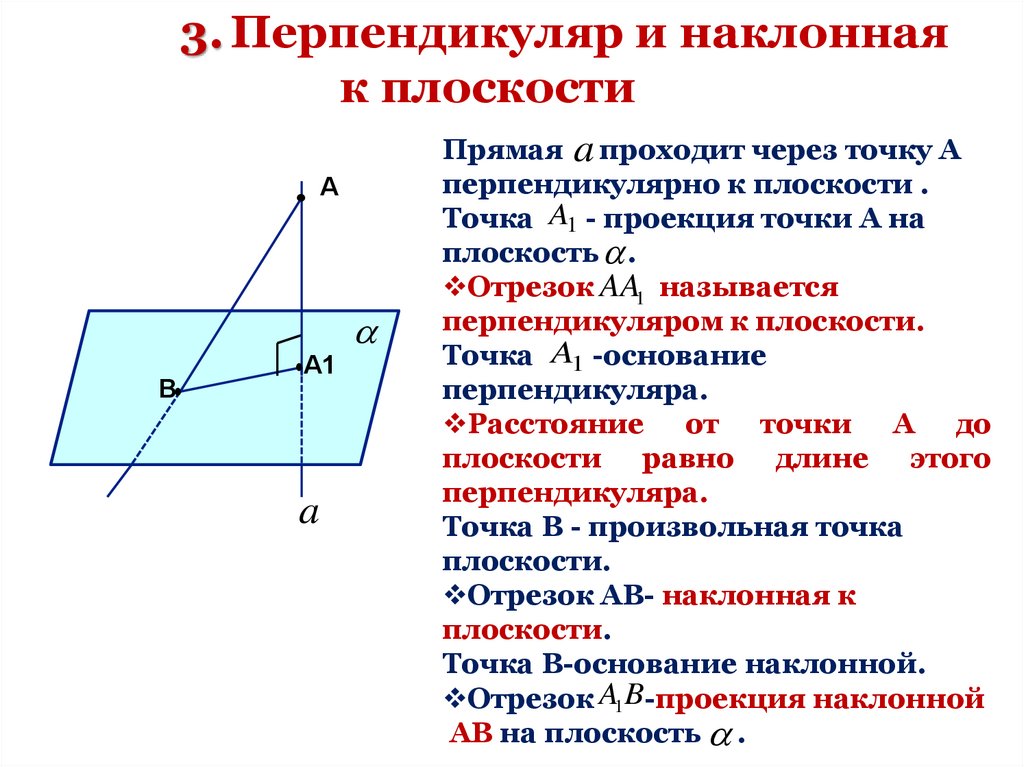
3. Перпендикуляр и наклоннаяк плоскости
А
В
А1
a
Прямая a проходит через точку А
перпендикулярно к плоскости .
Точка A1 - проекция точки А на
плоскость .
Отрезок AA1 называется
перпендикуляром к плоскости.
Точка A1 -основание
перпендикуляра.
Расстояние от точки А до
плоскости равно длине этого
перпендикуляра.
Точка В - произвольная точка
плоскости.
Отрезок АВ- наклонная к
плоскости.
Точка В-основание наклонной.
Отрезок A1B-проекция наклонной
АВ на плоскость .
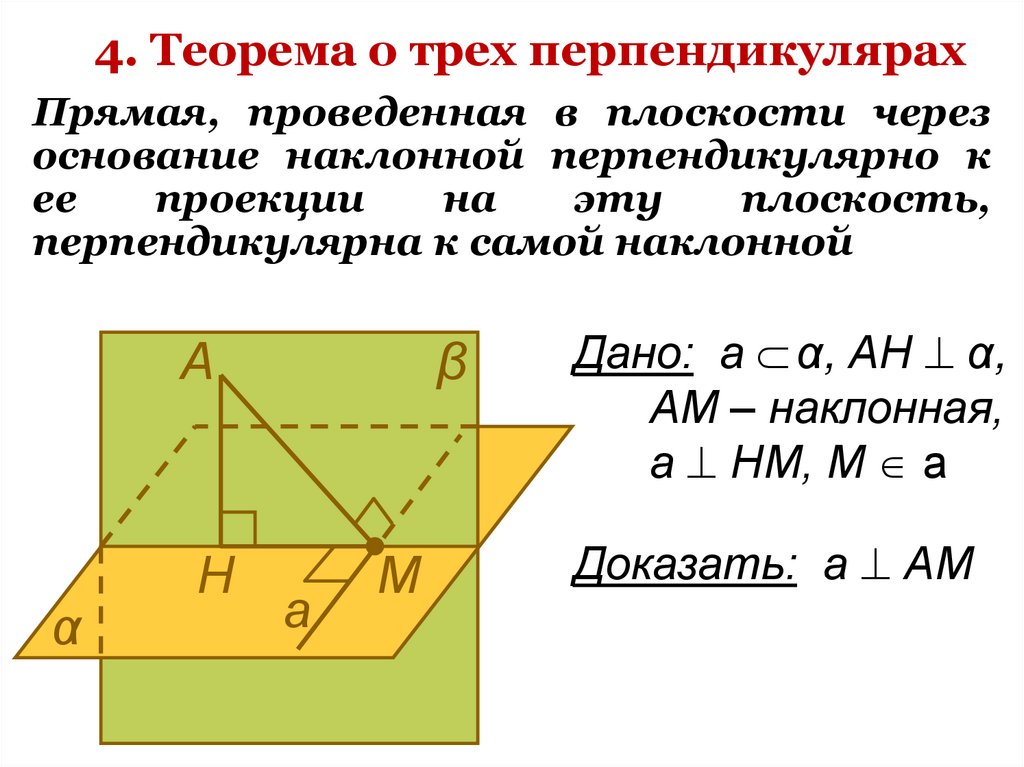
15. 4. Теорема о трех перпендикулярах
Прямая, проведенная в плоскости черезоснование наклонной перпендикулярно к
ее
проекции
на
эту
плоскость,
перпендикулярна к самой наклонной
А
α
Н
β
а
М
Дано: а α, АН α,
АМ – наклонная,
а НМ, М а
Доказать: а АМ
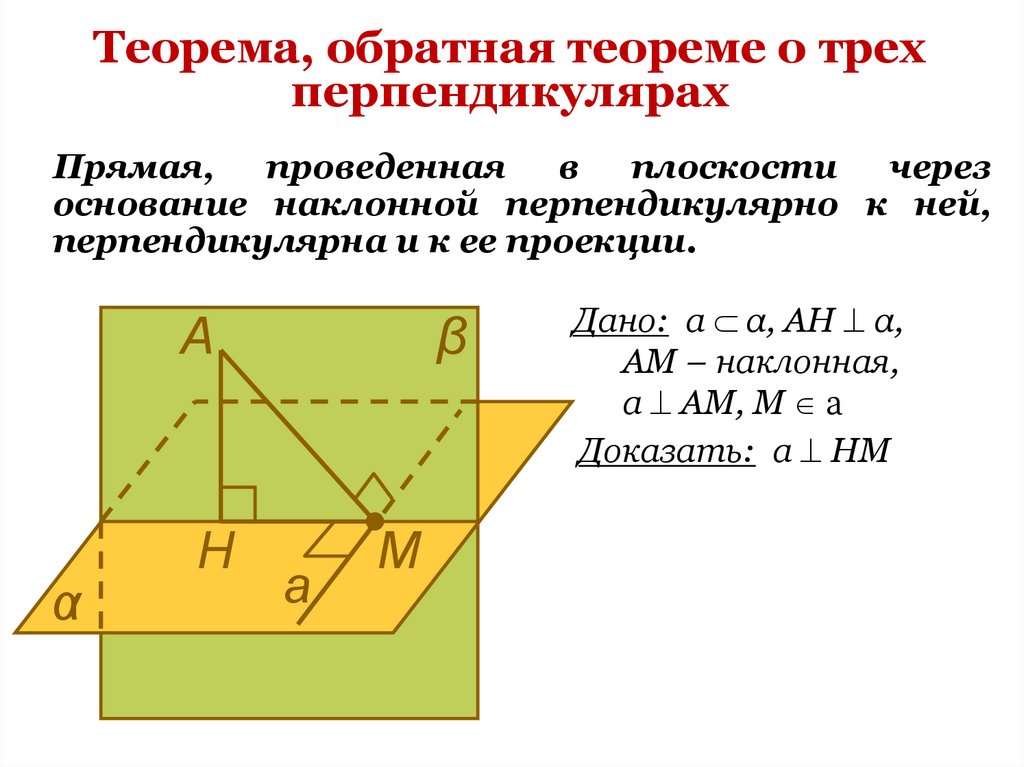
16.
Теорема, обратная теореме о трехперпендикулярах
Прямая,
проведенная
в
плоскости
через
основание наклонной перпендикулярно к ней,
перпендикулярна и к ее проекции.
А
α
Н
β
а
М
Дано: а α, АН α,
АМ – наклонная,
а АМ, М а
Доказать: а НМ
17.
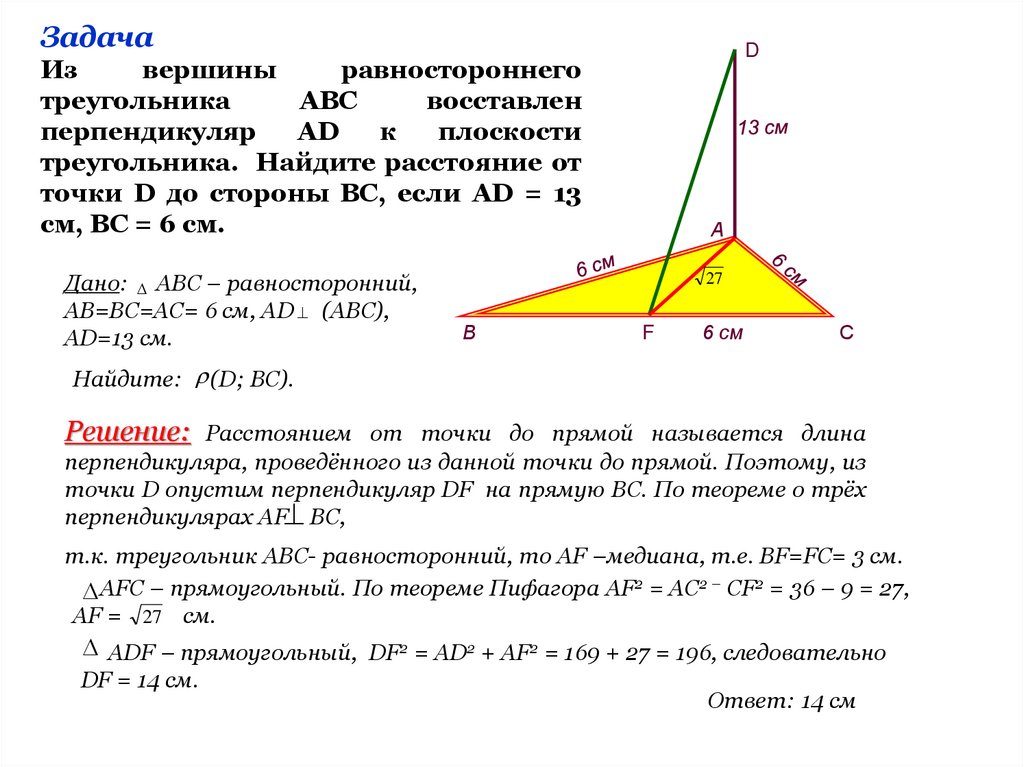
ЗадачаD
Из
вершины
равностороннего
треугольника
АВС
восставлен
перпендикуляр
AD
к
плоскости
треугольника. Найдите расстояние от
точки D до стороны ВС, если AD = 13
см, ВС = 6 см.
Дано: АВС – равносторонний,
АВ=ВС=АС= 6 см, АD (АВС),
АD=13 см.
А
27
В
F
6 см
С
Найдите: (D; BC).
Решение: Расстоянием от точки до прямой называется длина
перпендикуляра, проведённого из данной точки до прямой. Поэтому, из
точки D опустим перпендикуляр DF на прямую ВС. По теореме о трёх
перпендикулярах AF BC,
т.к. треугольник АВС- равносторонний, то АF –медиана, т.е. BF=FC= 3 см.
АFC – прямоугольный. По теореме Пифагора AF2 = AC2 – CF2 = 36 – 9 = 27,
AF = 27 см.
ADF – прямоугольный, DF2 = AD2 + AF2 = 169 + 27 = 196, следовательно
DF = 14 см.
Ответ: 14 см
18.
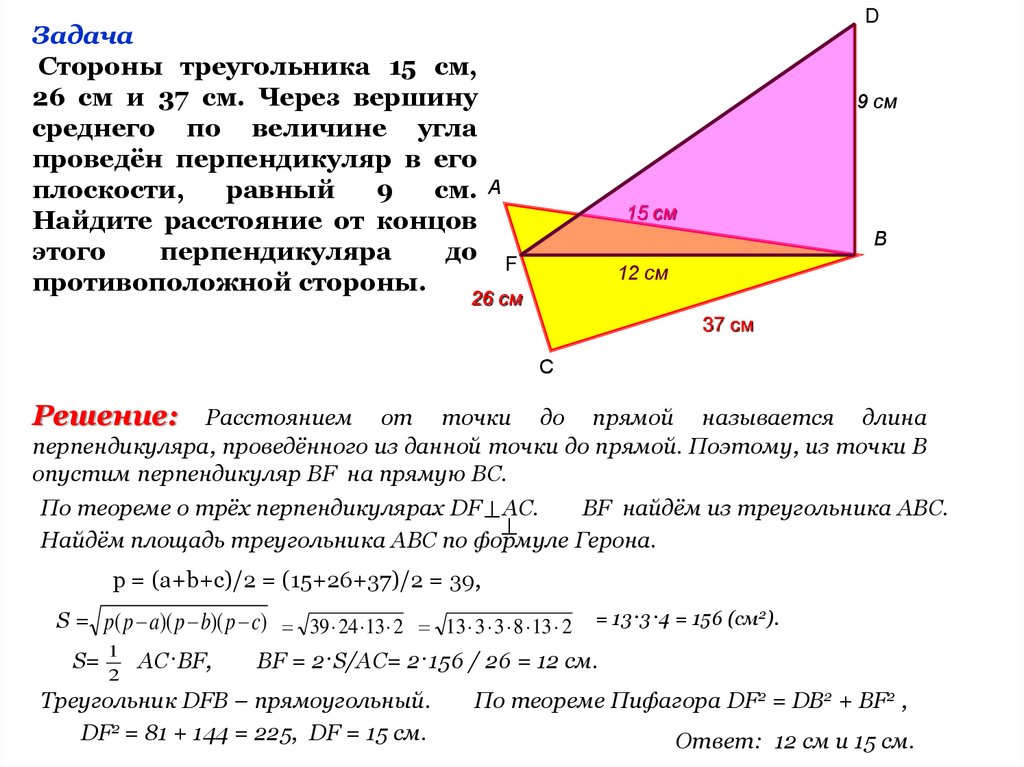
DЗадача
Стороны треугольника 15 см,
26 см и 37 см. Через вершину
среднего по величине угла
проведён перпендикуляр в его
плоскости,
равный
9
см. А
Найдите расстояние от концов
этого
перпендикуляра
до F
противоположной стороны.
9 см
15 см
В
12 см
26 см
37 см
С
Решение:
Расстоянием от точки до прямой называется длина
перпендикуляра, проведённого из данной точки до прямой. Поэтому, из точки В
опустим перпендикуляр ВF на прямую ВС.
По теореме о трёх перпендикулярах DF AC.
BF найдём из треугольника АВС.
Найдём площадь треугольника АВС по формуле Герона.
p = (a+b+c)/2 = (15+26+37)/2 = 39,
S = p( p a)( p b)( p c) 39 24 13 2 13 3 3 8 13 2 = 13·3·4 = 156 (см2).
S= 1 AC·BF,
2
BF = 2·S/AC= 2·156 / 26 = 12 см.
Треугольник DFB – прямоугольный.
DF2 = 81 + 144 = 225, DF = 15 см.
По теореме Пифагора DF2 = DB2 + BF2 ,
Ответ: 12 см и 15 см.
19.
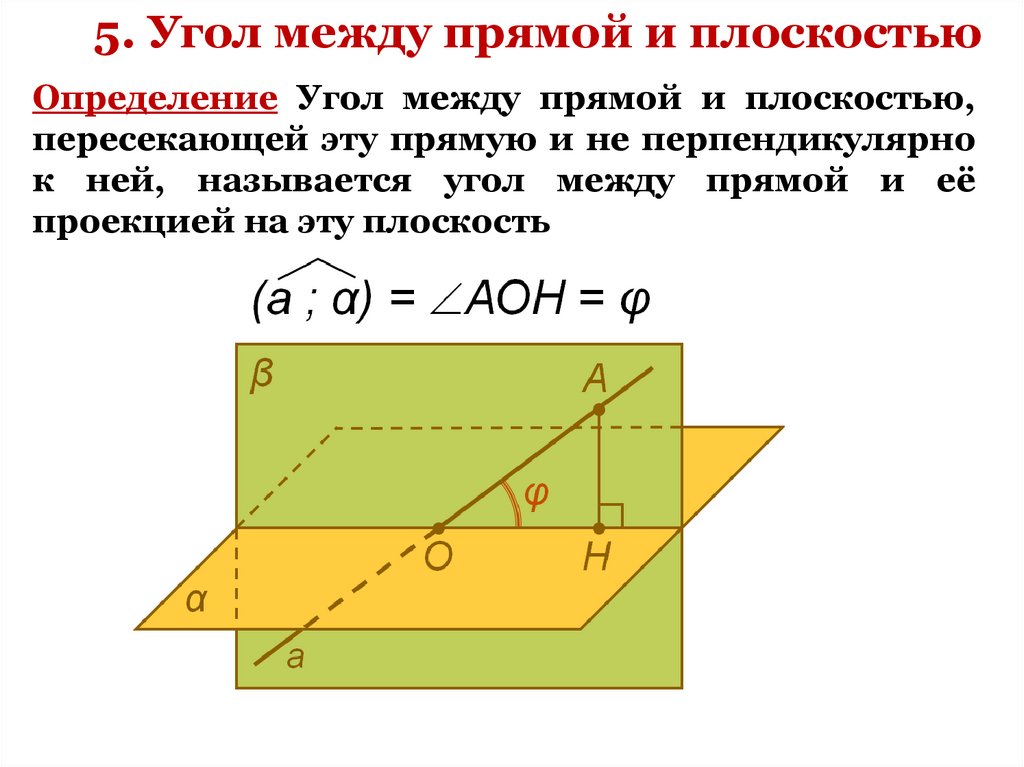
5. Угол между прямой и плоскостьюОпределение Угол между прямой и плоскостью,
пересекающей эту прямую и не перпендикулярно
к ней, называется угол между прямой и её
проекцией на эту плоскость
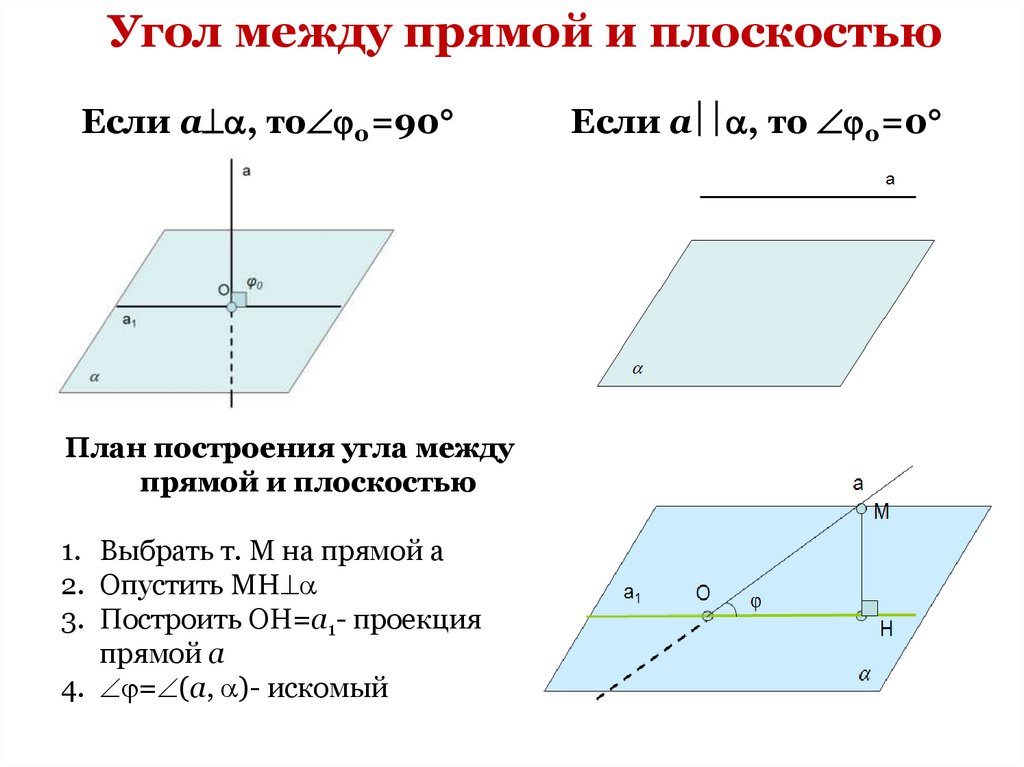
20. Угол между прямой и плоскостью
Если а , то 0=90План построения угла между
прямой и плоскостью
1. Выбрать т. М на прямой а
2. Опустить МН
3. Построить ОН=а1- проекция
прямой а
4. = (а, )- искомый
Если а , то 0=0


 mathematics
mathematics








