8СиТВ_Б_17_презентация

1.

Опыты с равновозможными
элементарными событиями.
Случайный выбор

2.

Задание 1
Решите задачи

3.

Задание 1
1) В среднем из каждых 80 поступивших в продажу
аккумуляторов только 76 заряжены. Найдите вероятность
того, что купленный аккумулятор не заряжен.
2) В мешке содержатся жетоны с номерами от 5 до 54
включительно. Какова вероятность того, что извлеченный
наугад из мешка жетон содержит двузначное число?
3) В чемпионате по футболу участвуют 16 команд, которые
жеребьевкой распределяются на 4 группы: A, B, C и D.
Какова вероятность того, что команда России не попадает в
группу A?
4) В лыжных гонках участвуют 11 спортсменов из России, 6
спортсменов из Норвегии и 3 спортсмена из Швеции.
Порядок, в котором спортсмены стартуют, определяется
жребием. Найдите вероятность того, что первым будет
стартовать спортсмен из России.

4.

Задание 1
5) Из каждых 1000 электрических лампочек 5
бракованных.
Какова
вероятность
купить
исправную лампочку при случайном выборе?
6) Петя, Вика, Катя, Игорь, Антон, Полина бросили
жребий – кому начинать игру. Найдите
вероятность того, что начинать игру будет
мальчик.
7) Из 1600 пакетов молока в среднем 80 протекают.
Какова вероятность того, что случайно выбранный
пакет молока не течет?
8) Определите вероятность того, что при бросании
игрального кубика (правильной кости) выпадет
нечетное число очков.

5.

Представим, что у вас в гардеробе есть двое
джинсов – черные (Ч), синие (С) и 3 футболки –
красная (К), белая (Б), желтая (Ж). Сколькими
способами вы сможете составить комплект одежды
для прогулки, состоящий из футболки и джинс?
Решение:
Составим все возможные варианты комплектов – ЧК, ЧБ,
ЧЖ, СК, СБ, СЖ. Таким образом получаем 6 вариантов.
Вопрос 1. Попробуйте сформулировать правило, по
которому можно будет рассчитать количество способов,
обоснуйте его.

6.

Комбинаторное правило
умножения
Если элемент А можно выбрать ! способами, а
другой объект В можно выбрать " способами, то
пару (А, В) можно выбрать ! # " способами.
Правило также верно для выбора по 1 элементу
из трех, четырех и т.д. групп.
Также комбинаторное правило умножения
называют правилом произведения.

7.

Представим, что у вас в гардеробе есть двое
джинсов – черные (Ч), синие (С) и 3 футболки –
красная (К), белая (Б), желтая (Ж). Сколькими
способами вы сможете составить комплект одежды
для прогулки, состоящий из футболки и джинс?
Решение:
Джинсы можно выбрать 2 способами. Футболку – 3
способами.
Значит, всего способов 2 " 3 = 6.

8.

Комбинаторика
–
это
раздел
математики, в котором изучаются
вопросы о том, сколько различных
комбинаций, подчиненных тем или иным
условиям, можно составить из заданных
объектов.

9.

Пример
2.
Сколько
четных
двузначных чисел можно составить из
цифр 0, 3, 2, 1, 4, 8, при условии, что
цифры могут повторяться?
Решение:
На первое место можно поставить 5 цифр
(так как с нуля число не может начинаться),
на второе – 4 (подходят 0, 2, 4, 8,). Значит,
всего 5 ∗ 4 = 20 чисел можно составить.

10.

Задание 2
В отеле три корпуса, и номера комнат обозначаются
номером корпуса и порядковым номером комнаты в
корпусе – в каждом корпусе номера комнат имеют 4
возможных значения – 1, 2, 3, 4. Например номера
комнат могут выглядеть так – 1-2 или 3-4. Сколько
всего номеров комнат в этом отеле?

11.

Задание 3
Сколько можно составить различных комбинаций
блюд, выбирая:
А) первое блюдо из 6 вариантов, второе – из 5;
Б) первое блюдо из 10 вариантов, второе – из 8.

12.

Пример 3. В спортивной секции, в которой 20
человек, проходят выборы капитана команды и его
помощника. Найдите вероятность того, что:
а) Ирина станет капитаном, а Андрей –
помощником.
б) Ирина и Андрей займут эти посты, неважно кто
именно
займёт
конкретный
пост.
в)
Андрей
станет
капитаном
команды.
Общее количество возможных вариантов:
! = 20 ∗ 19 = 380
а) * +
,
=
-./

13.

б) Ирина и Андрей займут эти
посты, неважно кто именно займёт
конкретный
пост.
Здесь нам подходит 2 случая: Ирина –
капитан, а Андрей – помощник, и наоборот.
Значит:
2
1
! " =
=
380 190

14.

в) Андрей станет капитаном команды.
Существует 19 вариантов пар, в которых
Андрей будет капитаном, так как когда
выберут Андрея, останется 19 претендентов
на место помощника. Все эти события
являются благоприятствующими.
19
! " =
= 0,05
380

15.

Задание 4
В классе 5 девочек и 7 мальчиков.
Необходимо выбрать капитана и его
заместителя. Какова вероятность
того, что капитаном станет девочка,
а заместителем – мальчик?

16.

Пример 4
Интерактивный
пример

17.

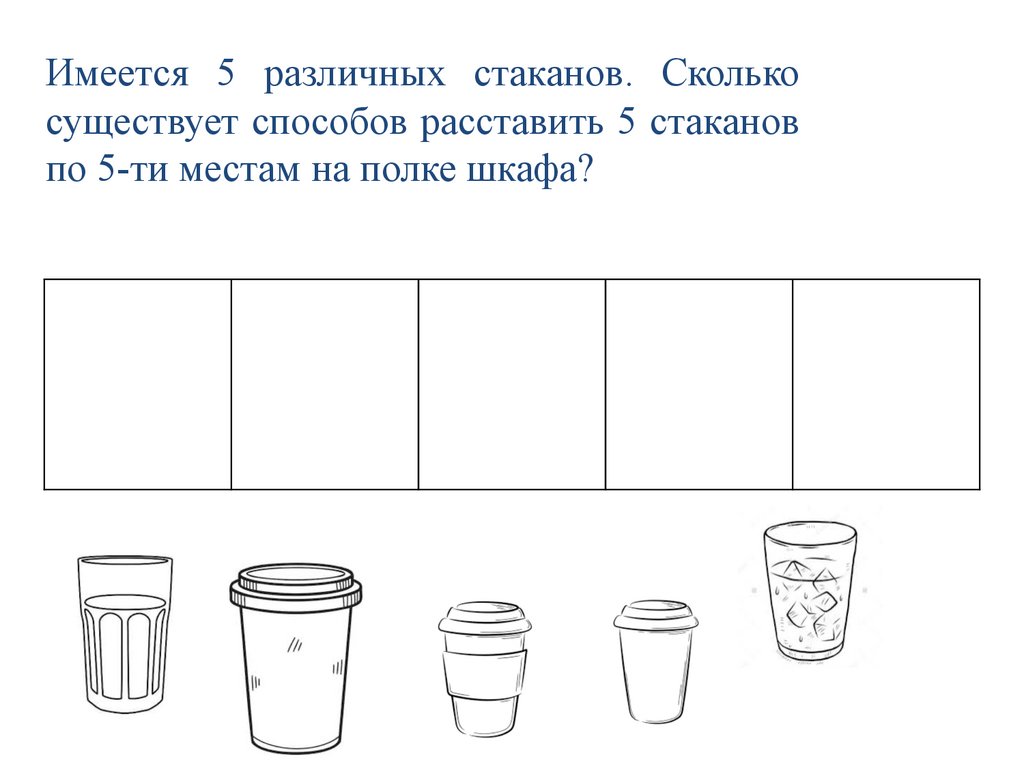
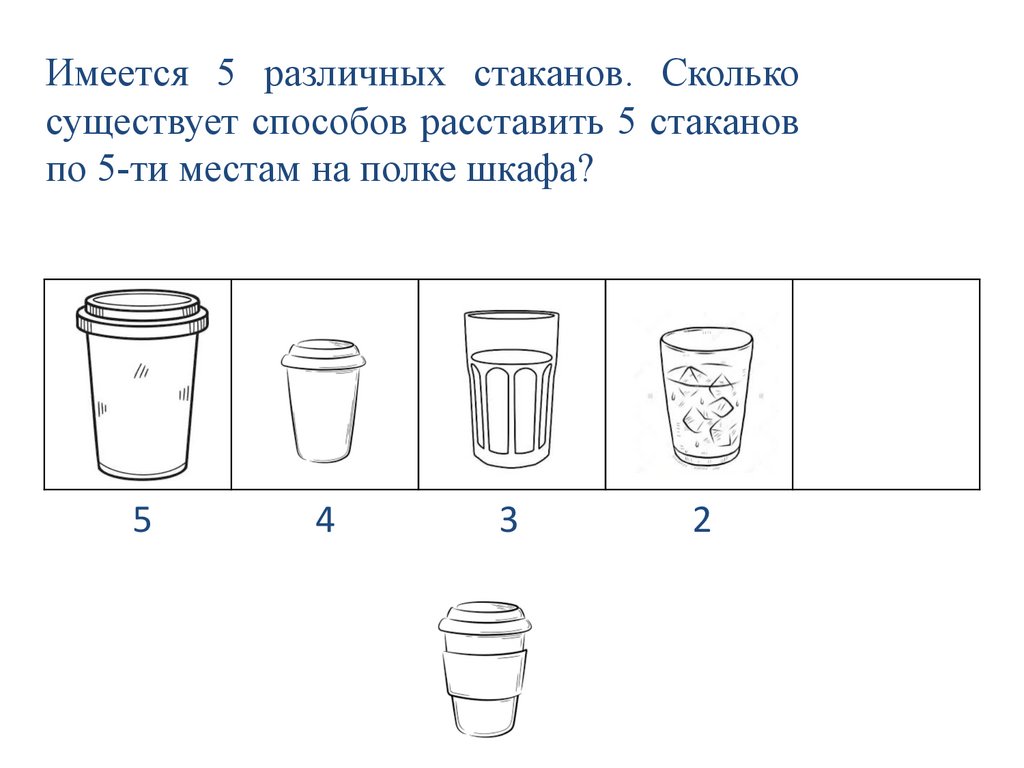
Имеется 5 различных стаканов. Сколько
существует способов расставить 5 стаканов
по 5-ти местам на полке шкафа?

18.

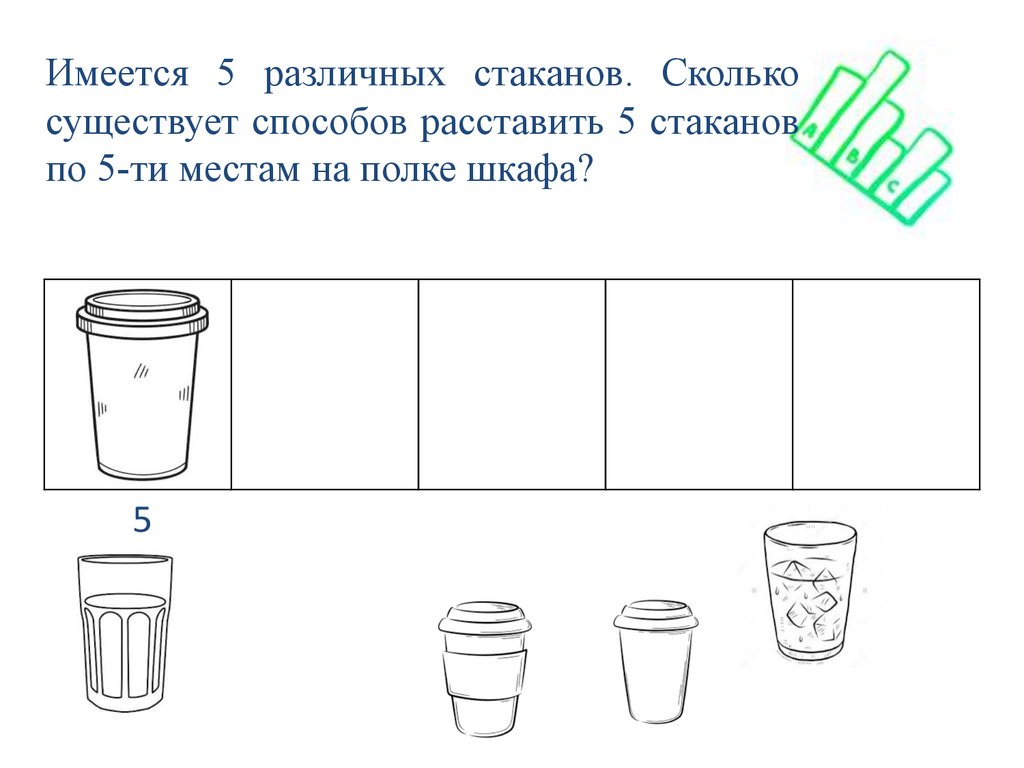
Имеется 5 различных стаканов. Сколько
существует способов расставить 5 стаканов
по 5-ти местам на полке шкафа?
5

19.

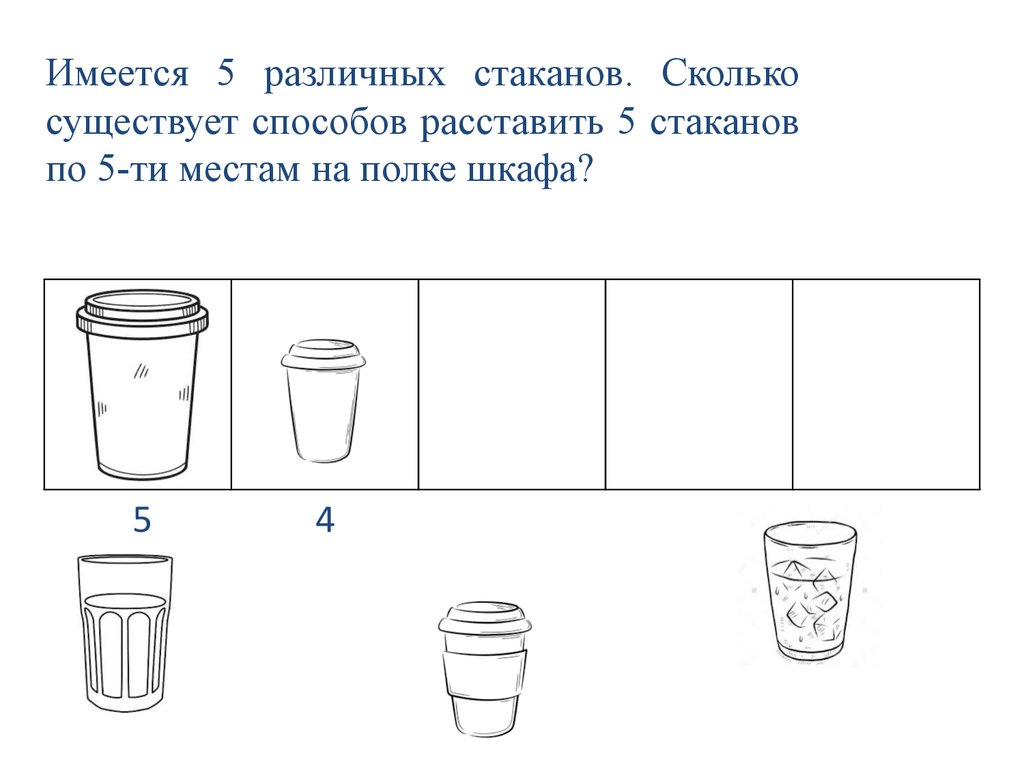
Имеется 5 различных стаканов. Сколько
существует способов расставить 5 стаканов
по 5-ти местам на полке шкафа?
5
4

20.

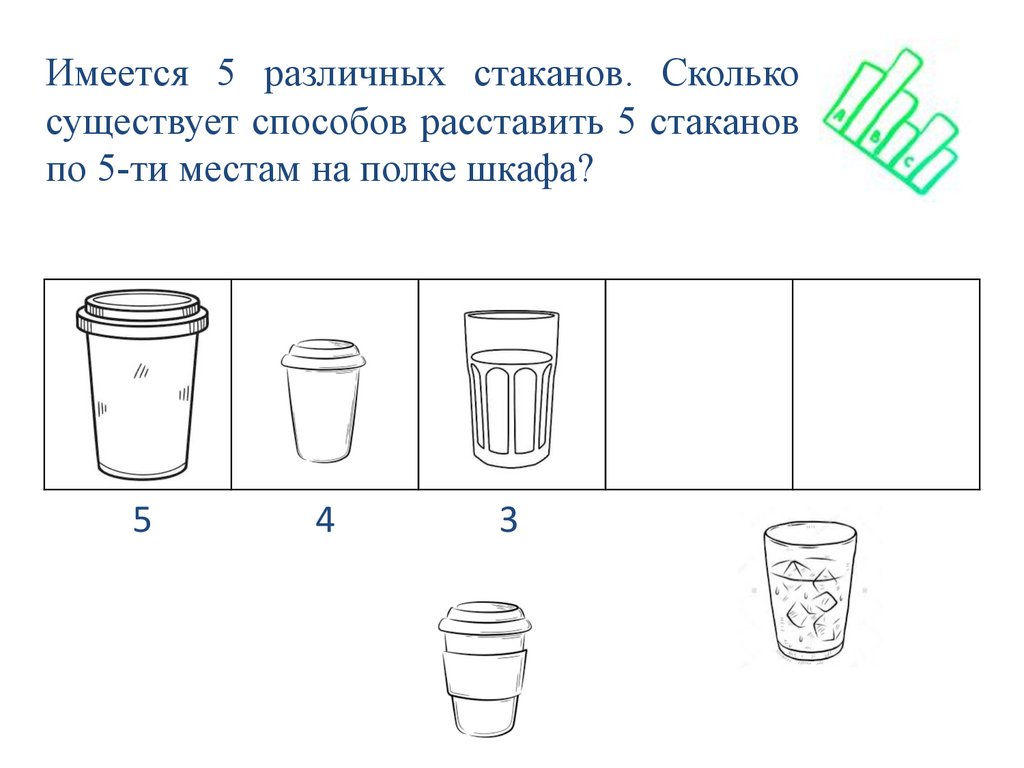
Имеется 5 различных стаканов. Сколько
существует способов расставить 5 стаканов
по 5-ти местам на полке шкафа?
5
4
3

21.

Имеется 5 различных стаканов. Сколько
существует способов расставить 5 стаканов
по 5-ти местам на полке шкафа?
5
4
3
2

22.

Имеется 5 различных стаканов. Сколько
существует способов расставить 5 стаканов
по 5-ти местам на полке шкафа?
5
4
3
2
Таким образом общее количество способов –
5*4*3*2*1=120 различных перестановок
1

23.

Вопрос 2. А сколько будет способов
переставить 6 различных стаканов
по 6-ти местам? А 7 стаканов
различных по 7-ми местам?

24.

Вопрос 2. А сколько будет способов
переставить 6 различных стаканов
по 6-ти местам? А 7 стаканов
различных по 7-ми местам?
6 стаканов – 6*5*4*3*2*1=720 перестановок
7 стаканов – 7*6*5*4*3*2*1=50.400 перестановок

25.

Вопрос 3. А сколько будет
способов
переставить
!
предметов?
1 ∗ 2 ∗ 3 ∗ ⋯ (( − 1) ∗ ( перестановок

26.

Факториалом натурального числа !
называется
произведение
всех
натуральных чисел от 1 до " .
Обозначение – "!
"! = 1 ∗ 2 ∗ 3 ∗ ⋯ (" − 1) ∗ "
Важно! По определению считается, что
0! = 1

27.

Назовем перестановкой из ! предметов
любой способ нумерации этих предметов
(способ их расположения в ряд).
Число перестановок ! предметов равно
"! и обозначается $% = "!

28.

Пример 5. Сколькими способами
можно рассадить 6 различных
людей на скамейке с 6-ю местами?
Решение:
количество
способов
рассадить 6 человек равно количеству
перестановок
6-ти
объектов.
Следовательно, 6! = 720
Ответ: 720.

29.

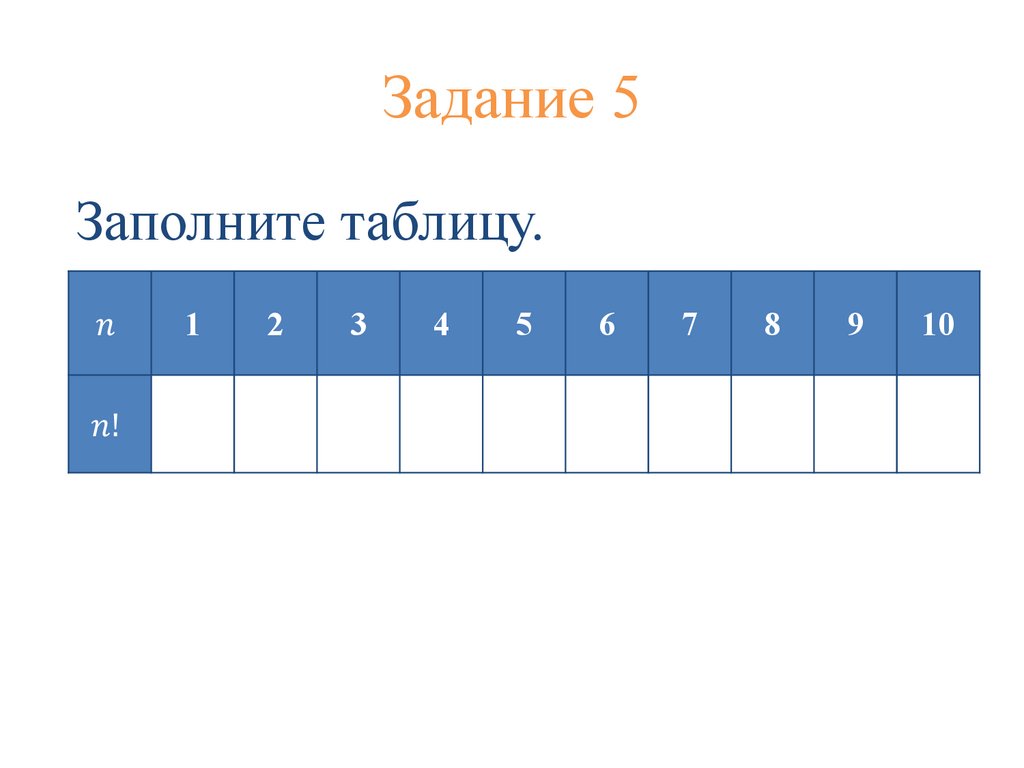
Задание 5
Заполните таблицу.
!
!!
1
2
3
4
5
6
7
8
9
10

30.

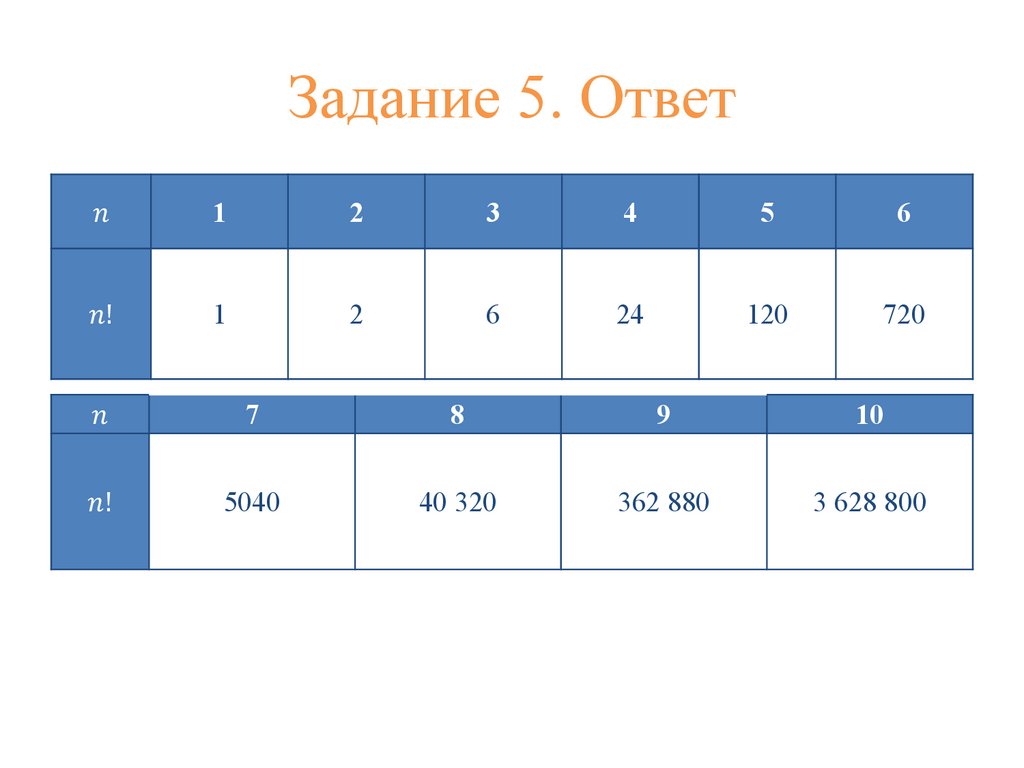
Задание 5. Ответ
!
1
2
3
4
5
6
!!
1
2
6
24
120
720
!
7
8
9
10
!!
5040
40 320
362 880
3 628 800

31.

Задание 6
Сколько существует трёхзначных чисел,
состоящих из цифр 3, 7, 8, при условии,
что каждая цифра встречается ровно
один раз?

32.

Задание 7
Найдите вероятность того, что
трехзначное
число,
которое
делится на 5, содержит цифру 2.

33.

Задание 8
Слово «ДОМ» написали на картонке и
разрезали её на буквы. Затем в случайном
порядке буквы выкладывают на стол.
Найдите вероятность того, что получилось
слово «МОД».

34.

Задание 9
На концерт заявлены 3 группы – А,
Б, В, которые должны выступить в
случайном
порядке.
Найдите
вероятность того, что группа А
будет выступать первой.

35.

Задание 10
Марина купила 3-х кроликов: серого (С), белого
(Б) и рябого (Р). Сколько существует различных
способов посадить этих кроликов в 3 клетки,
если в одной клетке может находиться
только 1 кролик? Найдите вероятность того, что:
а) В первой клетке сидит серый кролик, во
второй – белый, в третьей – рябой.
б) В первой клетке сидит рябой кролик, во
второй клетке – белый кролик.
в) В первой клетке сидит серый кролик.

36.

Задание 11
Сколько различных слов можно составить из
букв – М, А, Р, К, при условии, что словом
считается любая последовательность из 4 букв
без повторений?
1)Чему равна вероятность того, что при
случайном выборе слова из данных будет
выбрано слово МАРК?
2)Чему равна вероятность того, что при
случайном выборе слова из данных, будет
выбрано слово, у которого вторая буква А?

37.

Задание 12
На пяти одинаковых по размеру карточках
написаны буквы К, Р, А, Ш, И. Карточки
перемешиваются и наугад раскладываются в
ряд. Какова вероятность того, что получится
слово "ШАРИК"?

38.

Задание 13
Сколько различных пятизначных чисел можно
составить из цифр 2, 5, 8, 6, 1, так чтобы не было
одинаковых цифр и при условии, что:
1) первая цифра 8;
2) вторая цифра – 5, а пятая цифра – 1;
3) первая и вторая цифры – 5 и 6, в любом порядке.

39.

Задание 14
На полке стоят 4 книги 4-х авторов – Пушкина,
Достоевского, Ахматовой, Есенина. Сколькими
способами их можно расположить в случайном
порядке? Какова вероятность того, что:
1) книга Пушкина будет стоять на первом месте?
2) они будут стоять в алфавитном порядке слеванаправо?

40.

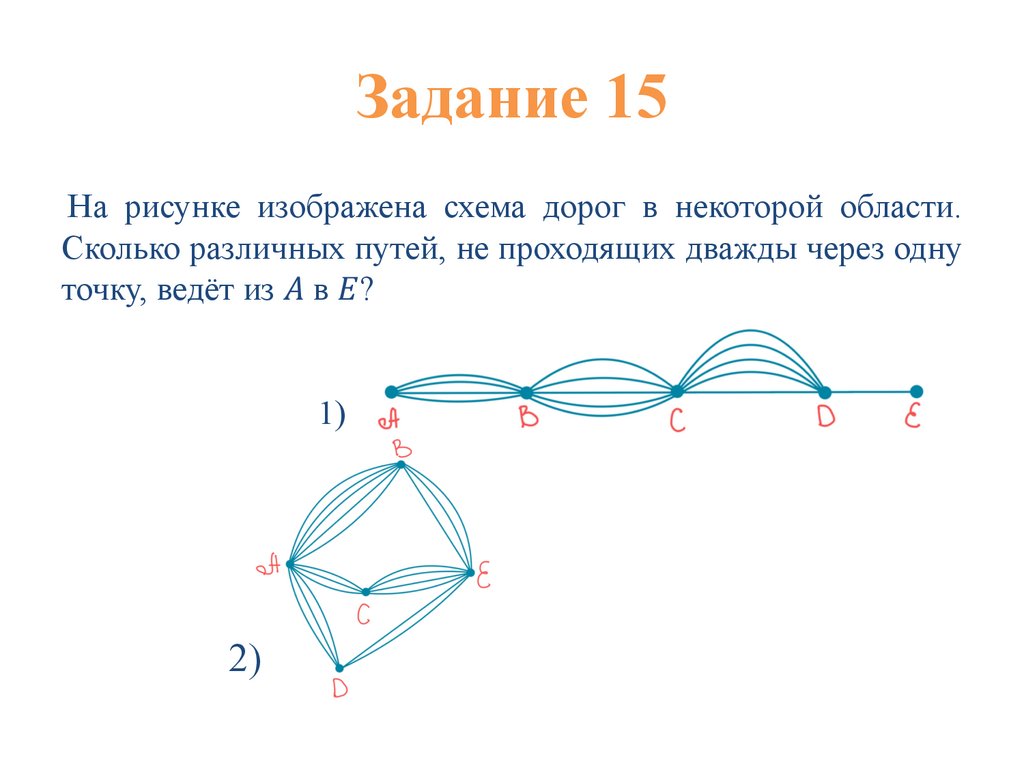
Задание 15
На рисунке изображена схема дорог в некоторой области.
Сколько различных путей, не проходящих дважды через одну
точку, ведёт из ! в "?
1)
2)

41.

Задание 16
Сколько различных трехзначных чисел, в которых
цифры могут повторяться, можно записать с
помощью цифр:
1) 1, 2, 3.
2) 0, 5, 9.
3) 3, 5, 6, 0, так чтобы число было нечетным.
4) 5, 6, 2, 9, 3, 0 так чтобы число было четным.

42.

Задание 17
На соревнованиях необходимо распределить
3 медали (золото, серебро и бронзу) между 8
участниками. Сколькими способами можно
это сделать, если каждый участник может
получить только одну медаль?

43.

Задание 18
Сколько различных четырехбуквенных слов,
не обязательно имеющих смысл, можно
составить из букв:
1)А, Р.
2)К, Е, Л.
3)С, Т, У, Л, Ь, Я.

44.

Задание 19
Сколько существует четырёхзначных
чисел, которые делятся на 5?

45.

Задание 20
Перед новым годом девочки решили, что
каждая из них подарит мальчику по открытке,
а мальчики решили, что каждый из них
подарит каждой девочке по коробке с
угощениями. Чего будет больше подарено:
открыток или коробок с угощениями?

46.

Задание 21
Найдите вероятность того, что в pin-код от
банковской карточки содержится цифра 5
(pin-код состоит из 4 цифр).

47.

Задание 22
Перед игрой в пейнтбол встретились две
команды. Каждый игрок команды пожал руку
каждому игроку другой команды. Всего было
221 рукопожатие. Сколько игроков в каждой
команде?

48.

Задание 23
Сколько существует вариантов номерных
знаков для машин с регионом 63? ГОСТом
для использования на знаках разрешены
буквы кириллицы, имеющие графические
аналоги в латинском алфавите. Номер не
может быть вида ∗ 000 ∗∗.
Пример номерного знака.

49.

Задание 24*
Найдите вероятность того, что Марии
достанется
номерной
знак
с
тремя
одинаковыми цифрами (без учета цифр в
регионе), при условии, что она живет в 63
регионе. Пример номерного знака приведен в
задании 23.