Similar presentations:
Лекция 9_merged
1.
МИРЭА – Российский технологический университетИнститут перспективных технологий
и индустриального программирования
ДИСКРЕТНАЯ МАТЕМАТИКА
Профессор кафедры индустриального программирования
Д-р. техн. наук, доцент
Фроленкова Лариса Юрьевна
2025
2.
Лекция 9 Оптимальное кодированиеЭнтропия текста. Сжатие текстов. Предварительное построение
словаря. Алфавитное кодирование. Префиксные схемы.
Неравенство Макмиллана. Оптимальное кодирование. Алгоритм
Хаффмана
2
3.
Теория кодирования – это раздел теории информации, изучающий способыотождествления сообщений с отражающими их сигналами. Задачей теории
кодирования является согласование источника информации с каналом связи.
–
Основоположником современной теории кодирования
считается американский инженер, криптоаналитик и математик
Клод Шеннон. Его работа «Математическая теория связи»,
опубликованная в 1948 году, заложила фундамент этой области.
Однако, теория кодирования – это обширная область, и вклад в нее
внесли многие ученые. Среди них можно выделить Ричарда
Хэмминга (занимался разработкой кодов, исправляющих
ошибки); Аллана Пайвио (создатель теории двойного кодирования
обработка и запоминание информации сознанием) и др.
Кодирование буквально пронизывает информационные технологии и
является центральным вопросом при решении самых разных (практически
всех) задач программирования:
представление данных произвольной природы (например, чисел, текста,
графики) в памяти компьютера;
- защита информации от несанкционированного доступа;
- обеспечение помехоустойчивости при передаче данных по каналам связи;
- сжатие информации в базах данных.
3
4.
Кодированием называют универсальный способ отображения информациипри ее хранении, обработке и передаче в виде системы соответствий между
сигналами и элементами сообщений, при помощи которых эти элементы можно
зафиксировать.
Объектом кодирования служит как дискретная, так и непрерывная
информация, которая поступает к потребителю через источник информации.
Понятие кодирование означает преобразование информации в форму,
удобную для передачи по определенному каналу связи.
Обратная операция – декодирование – заключается в восстановлении
принятого сообщения из закодированного вида в общепринятый, доступный
для потребителя.
Физическая величина, используемая для кодирования сообщений с
целью их хранения или передачи от источника информации к получателю,
называется сигналом.
Информация – все сведения, являющиеся объектом хранения, передачи
и преобразования. Информация, выраженная в определенной форме,
называется сообщением.
4
5.
Количество информации по Хартли и ШеннонуПонятие количество информации отождествляется с
понятием информация. Эти два понятия являются синонимами.
Впервые дать меру количества информации попытался в 1928 г.
Ральф Хартли, при этом Хартли наложил ряд ограничений:
1) рассматриваются только дискретные сообщения;
2) множество различных сообщений конечно;
3) символы, составляющие сообщения равновероятны и независимы.
В этом простейшем случае число N различных сообщений длиною в k
символов из алфавита содержащего m символов, равно mk, например, алфавит
состоит из трех символов: a, b, c, а k = 2. Тогда количество различных сообщений будет
составлять N = 32 = 9. Это будут aa, ab, ac, ba, bb, bc, ca, cb, cc. Если k = 3 то мы уже получим
N = 33 = 27 различных сообщений. То есть с увеличением длительности сообщений растет и
количество информации. И в этом случае, казалось бы, в качестве меры информации можно
было бы взять число N различных сообщений. Но Хартли указал, что экспоненциальная
зависимость N от k не позволяет использовать величину N в качестве меры информации.
Хартли впервые предложил в качестве меры количества информации
принять логарифм числа возможных последовательностей символов:
I log mk log N .
5
6.
Если I = log2 N, где log2 – функция логарифма по основанию 2, обратная возведениюзначения основания логарифма в степень, равную I, т.е. из формулы Хартли следует
зависимость N = 2 I.
Для облегчения вычислений для значений N, представляющих собой степени числа 2,
можно составить таблицу
N
2
4
8
16
32
64
128
256
512
1024
I (бит)
1
2
3
4
5
6
7
8
9
10
Для значений N, не равных степени двойки, при определении количества информации в
битах из вышеприведенной таблицы берется ближайшее большее значение N, равное
степени 2. Например, для 48 равновозможных событий, количество информации, которое
содержится в сообщении о совершении конкретного события, принимается равным 6 бит
(так как ближайшее большее значение, равное степени числа 2 равно 64).
При измерении количества информации Р. Хартли не учитывал
вероятность наступления события. Клод Шеннон попытался снять те
ограничения, которые наложил Хартли. На самом деле в рассмотренном
выше случае равной вероятности и независимости символов при любом k все
возможные сообщения оказываются также равновероятными, вероятность
каждого из таких сообщений равна P 1 N . Тогда количество информации
можно выразить через вероятности появления сообщений I log P .
6
7.
Пусть вероятность i-го символа (i = 1, 2, …, m) равна pi. Символыm
образуют полную группу событий, то есть, pi 1. Чтобы сообщения были
i 1
равновероятными, необходим чтобы относительные частоты появления отдельных
символов во всех возможных сообщениях были равны. При ограниченной длине сообщений
– это условие не выполняется. Но при достаточно длинных сообщениях условие равной
вероятности возможных сообщений будет, приближенно выполнятся.
В силу статистическойнезависимостисимволов, вероятность сообщения длиной
k
в k символов равна P pi . Если i-й символ повторяется в данном сообщении ki
i 1
m
раз, то P pik , так как при повторении i символа k i раз k уменьшается до m. Из
i
i 1
теории вероятностей известно, что, при достаточно длинных сообщениях (большое
число символов k) ki k pi и тогда вероятность сообщений будет равняться
m
P p
i 1
k pi
i
m
I log P log p
i 1
k pi
i
m
m
i 1
i 1
k pi log pi k pi log pi
формулой Шеннона для определения количества информации.
–
7
8.
Формула Шеннона дает более полное представление об источникеинформации, чем формула Хартли.
Например, если мы подбрасываем монету, то получим сообщение из двух возможных
состояний (орел или решка), то есть, алфавит сообщений из двух букв. Если подбрасываем
кубик, одна грань которого голубая, а остальные грани окрашены в розовый цвет, то здесь
также имеем алфавит из двух букв (голубой или розовый). Чтобы записать полученный текст
(сообщение), в обоих случаях достаточно одной двоичной цифры на букву (k = 1, т = 2).
По Хартли здесь в обоих случаях: I k log m 1 log 2 2 1. Но мы знаем, что в первом
случае вероятность каждого исхода опыта равна 0,5 (P1 = P2 = 0,5). А во втором случае
P1 1 6 и P2 5 6 соответственно. Мера Хартли не учитывает этого.
Формула Хартли является частным случаем формулы Шеннона. При равновероятных
символах, то есть при pi 1 m формула Шеннона переходит в формулу Хартли:
m
m
I k pi log pi k
1
m
1
log
k log m log mk log N .
m
Для случая с монетой: I 1 1 log 1 1 log 2 1 1.
2
2 2
2
2
Для случая с кубиком: I 1 1 log 1 5 log 2 5 0,195.
2
6
6
6 6
i 1
i 1
8
9.
Энтропия текста – это мера неопределенности или информационнойнасыщенности текста, основанная на теории информации Клода Шеннона. В
дискретной математике энтропия используется для анализа структуры
данных, сжатия информации и оценки сложности текстовых сообщений.
Количество информации I, приходящейся на один элемент сообщения k,
называется удельной информативностью или энтропией H.
m
I
H pi log pi – энтропия по Шеннону
k
i 1
Из формулы Шеннона следует, что количество информации, содержащейся
в сообщении, зависит от числа элементов сообщения k, алфавита т и
вероятностей выбора элементов pi. Зависимость I от k является линейной
I k H.
Количество информации и энтропия являются логарифмическими мерами и измеряются
в одних и тех же единицах. Основание логарифма определяет единицу измерения
количества информации и энтропии. Двоичная единица соответствует основанию
логарифма, равному двум, и называется битом. Один бит – это количество информации в
сообщении в одном из двух равновероятностных исходов некоторого опыта. Используются
также натуральные и десятичные логарифмы. Аналогичными единицами пользуются и при
оценке количества информации с помощью меры Хартли.
9
10.
Отметим некоторые свойства энтропии.1.
Энтропия является величиной вещественной, ограниченной и
неотрицательной, то есть H 0.
2. Энтропия минимальна и равна нулю, если сообщение известно заранее,
то есть если pi 1, а p1 p2 ... pi 1 pi 1 ... pk 0.
3. Энтропия максимальна, если все состояния элементов сообщений
1
равновероятны: H H max , если p1 p2 ... pi ... pm P .
m
m
1
1
Величина максимальной энтропии: H max log log m.
m
i 1 m
4. Энтропия бинарных (двоичных) сообщений может изменяться от нуля
до
единицы
(двоичный
алфавит,
следовательно,
т=2):
2
H pi log pi p1 log p1 p2 log p2 .
i 1
Используя
условие
m
pi 1 и
i 1
обозначив p1 p, получим p2 1 p1 1 p, а энтропия определится
выражением H p log p 1 p log 1 p .
10
11.
Энтропия достигает максимума, равного единице, при p1 p2 0,5.График функции H p log p 1 p log 1 p
Сжатие данных – важная задача в информатике и дискретной
математике, направленная на уменьшение объема хранимой или
передаваемой информации. Одним из наиболее эффективных подходов к
сжатию текстов является словарное сжатие, в основе которого лежит
использование словаря – набора часто встречающихся подстрок.
Словарное сжатие основано на идее замены повторяющихся
фрагментов текста на более короткие ссылки (указатели) на словарь. Этот
подход особенно эффективен для текстов с высокой степенью повторяемости, таких как
программный код, литературные тексты, HTML-документы и т.д.
11
12.
Принцип: пусть заданы: текст T t1t2 ...tn , где ti – символы из алфавита ∑;словарь D – это множество подстрок D d1, d2 , ..., dk , где di T ; каждая
подстрока di заменяется на ссылку ⟨i⟩ – индекс в словаре.
Пример: Исходный текст: «алгоритм – это алгоритм эффективного решения задачи»
Часто встречающаяся подстрока: «алгоритм». Словарь: D = {«алгоритм»}, индекс 0
Сжатый текст: «⟨0⟩ – это ⟨0⟩ эффективного решения задачи»
Таким образом, длина текста уменьшается за счет замены длинных подстрок на
короткие коды.
Рассмотрим математическую модель словарного сжатия.
Обозначения:
T t1t2 ...tn – исходный текст длины n;
D d1, d2 , ..., dk – словарь, где di – длина i-го слова;
fi – частота вхождения di в T;
Lorig n – исходная длина текста (в символах);
k
Ldict di – суммарная длина словаря;
i 1
12
13.
kLref c fi – длина ссылок, где c – длина кода ссылки (в битах или
i 1
символах);
Lcomp Ldict Lref – общая длина сжатого представления.
Степень сжатия определяется как: C Lorig Lcomp .
Выигрыш в размере: L Lorig Lcomp .
Чтобы сжатие было эффективным, необходимо: L 0 Lorig
Lc
Одним из ключевых этапов эффективного сжатия omp .
является
предварительное построение словаря – анализ текста до сжатия
для
выявления оптимальных подстрок, подлежащих включению в словарь.
Задача оптимизации – выбрать подмножество подстрок D Sub(T )
(множество D состоит только из элементов, которые сами являются подмножествами
k
множества T), максимальный выигрыш: max fi di Ldict Lref – это
D
i 1
задача дискретной оптимизации, которая является достаточно трудной в
общем случае.
13
14.
Один из практических подходов – «жадный алгоритм» (это алгоритм,который на каждом шаге выбирает локально оптимальное решение, надеясь, что в итоге
будет найдено глобально оптимальное решение. Этот подход не всегда приводит к
оптимальному решению, но часто используется из-за своей простоты и эффективности):
1) найти все подстроки длины ≥ 2 в тексте;
2) подсчитать частоту каждой подстроки;
3) вычислить выигрыш для каждой подстроки d: Gain(d) fd d c d ,
где: fd – частота; d – длина подстроки; c – длина ссылки (например, 1 символ
или 2 байта);
4) отсортировать подстроки по убыванию выигрыша;
5) добавить в словарь те подстроки, для которых Gain(d ) 0.
Замечание: При добавлении одной подстроки частоты других могут
измениться (из-за перекрытия), поэтому требуется итеративный
пересчет.
14
15.
Пример построения словаряРассмотрим текст: T = «abcabcabc defabc »; длина: 15 символов.
Подсчитаем частоты подстрок длины ≥ 3:
Выигрыш (при с = 1)
Длина Частота
Подстрока
d
Gain(d) fd d c d
fd
«abc»
3
4
4⋅(3−1)−3=8−3=5
«bca»
3
2
2⋅2−3=1
«cab»
3
2
2⋅2−3=1
«abcabc»
6
1
1⋅(6−1)−6=−1
Выбираем «abc» (выигрыш 5 > 0). Словарь: D = {«abc»}, индекс 0.
Сжатый текст: «⟨0⟩⟨0⟩⟨0⟩ def⟨0⟩». Дл ина словаря: 3. Количество
ссылок: 4 → длина ссылок: 4 (по 1 символу). Общая длина: 3 + 4 = 7.
Исходная длина: 15. Степень сжатия: C = 15/7 ≈ 2,14
Избыточность – мера неэффективности источника, показывает,
насколько больше бит используется, чем необходимо: 1 Н , где: H –
Нmax
реальная энтропия (на символ); Hmax – максимальная возможная энтропия
для алфавита из n символов.
15
16.
Графическое представлениеРисунок – Процесс словарного сжатия
Рисунок – Структура сжатого файла
16
17.
Предварительное построение словаря позволяет достичь высокой степени сжатия засчет анализа структуры данных до начала процесса.
Словарные методы кодирования используются при кодировании сообщений, между
которыми выявлены статистические связи. Так, если элементарными сообщениями
являются буквы русского алфавита (примем, что их число М = 32 = 25) и они передаются
равновероятно и независимо, то энтропия источника, приходящаяся на одну букву:
H (M ) log2 32 5.
Если же буквы составляют связный русский текст, то они оказываются
неравновероятными (например, буква «А» передается значительно чаще, чем буква «Ф») и,
главное, зависимыми. Так, после гласных не может появиться «ь», и др.
Подсчитано, что для текстов русской художественной прозы энтропия оказывается
менее 1,5 бит/букву и возможен способ эффективного кодирования текстов без потери
информации, при котором в среднем на одну букву будет затрачено не 5, а немногим более
1,5 двоичных символов, т. е. на 70 % меньше. Существует довольно много способов
сокращения избыточности текста. Так, вместо «ААА» можно закодировать «3А» или же
сокращать слова, как это делается в стенографии.
Особенно большой эффект дает укрупнение алфавита, когда кодируются не отдельные
буквы, а целые слова. В достаточно большом словаре имеется около 10 000 слов,
содержащих в среднем по 7 букв. На кодирование одной буквы русского алфавита требуется
5 двоичных символов, а на одно слово, состоящее из 7 букв, – 35 символов.
17
18.
Алфавитное кодирование – это способ отображения символов конечногоалфавита A a1, a2 , ..., an в последовательности из символов другого
алфавита (обычно двоичного: 0,1 ), называемые кодовыми словами.
Кодирование – это функция, отображающая элементы из множества A
(множество исходных данных) во множество последовательностей нулей и
единиц, представленных как 0, 1 (кодирование преобразует элементы исходного
*
*.
множества в последовательности битов (нулей и единиц)): C : A 0,1
Пример: Есть алфавит A a, b, c , и задано кодирование: C(a) 0, C(b) 10, C(c) 11
.
Тогда сообщение «abc» кодируется как: C(abc) C(a)C(b)C(c) 01011 01011.
Реализация кодирования на передающей стороне всегда предполагает
применение обратной процедуры – декодирования – для восстановления
принятого сообщения. Устройства, осуществляющие кодирование и
декодирование, называются соответственно кодер и декодер. Вместе их
называют кодеком.
18
19.
При кодировании важно, чтобы закодированное сообщение можно былооднозначно восстановить. Рассмотрим пример:
Символ
Код
a
0
b
01
c
11
Сообщение 011 может быть расшифровано как:
- 0 + 11 → a c;
- 01 + 1 → b ? так как 1 не является кодом!
Значит, только a c.
Но если бы код для c был 1, тогда 0 + 1 + 1 → a c с или 01 + 1 → b c →
неоднозначность.
19
20.
Префиксная схема, также известная как префиксный код, это такойспособ кодирования, в котором ни одно кодовое слово не является
префиксом другого кодового слова. Это свойство позволяет однозначно
декодировать последовательность кодов, даже если между ними нет
разделителей. То есть для любых двух кодовых слов C(x) и C(y), C(x) не
является началом C(y).
Пример префиксного кода
Символ
Код
Проверим префиксность:
a
0
0 – не префикс 10, 110, 111
b
10
10 – не префикс 110, 111
c
110
110 – не префикс 111
d
111
111 – не префикс других
✅ Префиксный код.
Сообщение 110010111 разбивается: 110 → c; 0 → a; 10 → b; 111 → d
→cabd
20
21.
Префиксные коды удобно представлять с помощью бинарного дерева.Корень (root) – начало кода. Левое ребро – 0, правое – 1. Каждый лист –
кодовое слово для символа.
Пример дерева для кода:
Символ
Код
Путь от корня:
до a: 0
a
0
до b: 1 → 0 = 10
до c: 1 → 1 → 0 = 110
b
10
до d: 1 → 1 → 1 = 111
c
110
d
111
21
22.
Для существования однозначно декодируемого кода необходимо иn
достаточно, чтобы выполнялось неравенство:
q
l i
1 неравенство
i 1
Крафта–Макмиллана, где n – количество букв в исходном алфавите; q –
количество букв в кодирующем алфавите; l1, l2, …, ln – длины кодовых слов.
Пример 1: Двоичный код. Пусть q 2 , алфавитный источник S a, b, c, d , длины
кодовых слов: la 1, lb 2, lc 3, ld 3.
Проверим неравенство: 2 1 2 2 2 3 2 3 0,5 0, 25 0,125 0,125 1,0 1 – ✅
неравенство выполнено, значит, существует однозначно декодируемый код с такими
длинами, например: a → 0; b → 10; c → 110; d → 111.
Пример 2: Недопустимый код. Пусть q 2 , алфавитный источник S a, b, c , длины
кодовых слов: la 1, lb 1, lc 2.
Проверим неравенство: 2 1 2 1 2 2 0,5 0,5 0, 25 1,25 1 – ✅ неравенство не
выполняется, значит, однозначно декодируемый код с такими длинами не существует.
Неравенство
Крафта-Макмиллана
– это важное условие
существования префиксного кода с заданными длинами кодовых слов. Для
существования префиксного двоичного кода с длинами кодовых слов l1, l2,
n
…, ln необходимо и достаточно выполнение неравенства: 2 l i 1.
i 1
22
23.
Чтобы оценить эффективность кода, вводится средняя длина кодовогоn
слова: L pi li , где: pi – вероятность появления символа ai ; li – длина
i 1
кодового слова для ai .
Пример:
Пусть даны вероятности: p(a) 0,5; p(b) 0,25; p(c) 0,125; p(d ) 0,125.
Код: C(a) 0 la 1; C(b) 10 lb 2 ; C(c) 110 lc 3 ; C(d ) 111 ld 3.
Средняя длина:
L 0,5 1 0, 25 2 0,125 3 0,125 3 0,5 0,5 0,375 0,375 1,75 бит.
23
24.
Прямая теорема побуквенного неравномерного кодирования. Дляисточник информации с алфавитом S s1, s1, ..., sn и вероятностями
n
символов p1, p2, …, pn с энтропией H (S) pi log2 pi существует
i 1
побуквенный неравномерный префиксный двоичный код со средней длиной
кодовых слов L H (S ) 1.
Пример 1: Двоичный код для источника с тремя символами
Пусть алфавит источника S a, b, c с вероятностями: p(a) 0,5; p(b) 0,25;
p(c) 0, 25.
Энтропия источника:
H (S) 0,5log2 0,5 0, 25log2 0, 25 0, 25log2 0, 25 0,5 0,5 0,5 1,5 бит .
Согласно теореме, можно построить код со средней длиной L, сколь угодно близкой к
1,5 битам. Пример кода: a: 0 (1 бит); b: 10 (2 бита); c: 11 (2 бита).
Средняя длина: L 0,5 1 0,25 2 0, 25 2 0,5 0,5 0,5 1,5 бит .
Здесь L H (S ) , что удовлетворяет теореме.
24
25.
Обратная теорема побуквенного неравномерного кодирования. Дляисточника информации с алфавитом S s1, s1, ..., sn и вероятностями
n
символов p1, p2, …, pn с энтропией H (S) pi log2 pi средняя длина
i 1
кодовых слов L удовлетворяет неравенству L H (S ).
Пример 2: Двоичный код для источника с четырьмя символами
Пусть алфавит источника S a, b, c, d с вероятностями: p(a) 0,5; p(b) 0,25;
p(c) 0,125; p(d ) 0,125
Энтропия источника:
H (S) 0,5log2 0,5 0,25log2 0,25 0,125log2 0,125 0,125log2 0,125
0,5 0,5 0,375 0,375 1,75 бит.
Согласно обратной теореме, средняя длина кодового слова L любого однозначно
декодируемого кода для этого источника не может быть меньше 1,75 бит.
Пример кода: a: 0 (1 бит); b: 10 (2 бита); c: 110 (3 бита); d: 111 (3 бита).
Средняя длина:
L 0,5 1 0,25 2 0,125 3 0,125 3 0,5 0,5 0,375 0,375 1,75 бит.
Здесь L H (S ) , что удовлетворяет обратной теореме.
25
26.
Алгоритм кодирования Шеннона–ФаноКодирование Шеннона-Фано является одним из самых первых алгоритмов сжатия, который
впервые сформулировали американские ученые Шеннон (Shannon 1948) и Фано (Fano).
Алгоритм кодирования кодом Шеннона–Фано включает в себя
следующее конечное число действий:
1.
Все сообщения источника располагают в таблице в один столбец в
порядке убывания их вероятностей.
2. Сообщения разбивают на две группы таким образом, чтобы суммарные
вероятности каждой из этих групп были по возможности почти равными.
3.
Сообщениям верхней группы в качестве первого символа кодового
слова присваивают символ «0», а нижнего – «1» (или наоборот).
4.
Каждая из полученных групп, если она содержит более одного
сообщения, делится на две подгруппы, имеющие по возможности равные
суммарные вероятности. В качестве второго символа кодового слова
используется «0» или «1» в зависимости от принадлежности сообщений
верхней или нижней подгруппе.
5.
Процесс повторяется до тех пор, пока в каждой подгруппе не останется
по одному сообщению.
26
27.
2728.
Алгоритм Хаффмана строит оптимальный префиксный код сминимальной средней длиной при заданных вероятностях:
1.
Все сообщения источника располагают в таблице в один (основной)
столбец в порядке убывания их вероятностей.
2.
Два самых маловероятных сообщения (два последних) объединяют в
одно и вычисляют их суммарную вероятность.
3.
Вероятность сообщений, не участвующих в объединении, и
вероятность полученного вспомогательного сообщения располагают во
вспомогательном столбце в порядке убывания вероятностей. При
необходимости во вспомогательном столбце проводят перегруппировку
вероятностей.
4.
Два самых маловероятных сообщения полученного вспомогательного
столбца объединяют в одно и вычисляют их суммарную вероятность.
5.
Повторяют шаги 3 и 4, создавая новые вспомогательные столбцы, до
тех пор, пока не получат единственное сообщение, вероятность которого
Р = 1.
28
29.
6. Строят кодовое дерево Хаффмана, начиная от сообщениявероятностью Р = 1. От этой вероятности отводят две ветви,
соответствующие двум вероятностям, давшим в сумме вероятность Р = 1,0.
Ветви с большей вероятностей присваивают символ «1», а с меньшей –
«0». Затем каждую из полученных ветвей вновь разветвляют на две, и так
продолжается до тех пор, пока не доходят до концевых узлов,
соответствующих вероятностям каждого из исходных сообщений. При
разветвлении ветви на две равновероятные одной из них присваивается «1»,
а другой – «0».
7. Кодируют исходные сообщения, двигаясь по ветвям кодового дерева в
направлении от вероятности Р = 1 к концевым узлам, соответствующим
определенным сообщениям.
29
30.
Пример. Требуется закодировать кодом Хаффмана восемь сообщений а1,а2, а3, а4, а5, а6, а7, а8 с вероятностями p(a1 ) 0,16; p(a2 ) 0,10; p(a3 ) 0, 04;
p(a4 ) 0,16; p(a5 ) 0,22; p(a6 ) 0,02; p(a7 ) 0,20; p(a8 ) 0,10;
Формирование вспомогательных столбцов кода Хаффмана
30
31.
Сообщениеа1(0,16)
а2(0,10)
а3(0,04)
а4(0,16)
а5(0,22)
а6(0,02)
а7(0,20)
а8(0,10)
Код
111
100
10101
110
01
10100
00
1011
31
32.
Для полученного кода среднее число символов «0» и «1», приходящихсяна одно закодированное сообщение составит:
nср 0, 22 2 0, 2 2 0,16 3 0,16 3 0,10 3 0,10 4 0,04 5 0,02 5 2,8.
Степень сжатия равна: 3 2,8 1,071.
Код Хаффмана минимизирует среднюю длину кода среди всех
префиксных кодов.
Применение: сжатие данных (форматы ZIP, PNG, MP3); передача
данных (модемы, спутниковая связь); хранение информации (Huffman coding
в JPEG); телекоммуникации.
Кодирование Шеннона-Фано является достаточно старым методом
сжатия, и на сегодняшний день оно не представляет особого практического
интереса. В большинстве случаев, длина сжатой последовательности, по
данному методу, равна длине сжатой последовательности с использованием
кодирования Хаффмана. Но на некоторых последовательностях все же
формируются не оптимальные коды Шеннона-Фано, поэтому сжатие
методом Хаффмана принято считать более эффективным.
Спасибо за внимание
32
33.
ДИСКРЕТНАЯ МАТЕМАТИКАРТУ МИРЭА
Профессор кафедры индустриального программирования
Д-р. техн. наук, доцент
Фроленкова Лариса Юрьевна
34.
Лекция 10 Помехоустойчивое кодированиеСхема
передачи
информации
по
каналам
связи.
Помехоустойчивое кодирование. Кодирование с исправлением
ошибок. Кодовое расстояние. Коды Хемминга. Код БЧХ.
2
35.
1 Схема передачи информации по каналам связиСхема передачи информации по каналам связи – это модель, описывающая
процесс передачи данных от источника к получателю через коммуникационный
канал. Классическая модель передачи информации была предложена Клодом
Шенноном в 1948 году. Она включает следующие компоненты:
источник информации – генерирует сообщение (текст, звук, данные и т.д.). Может
быть сопровождающим (например, текст) или непрерывным (аналоговый сигнал);
кодер (кодирующее устройство) – преобразует сообщение в виде последовательности
символов (обычно двоичных). Может включать: источниковое кодирование – сжатие
данных (удаление избыточности); канальное кодирование – добавление избыточности для
защиты от ошибок (помехоустойчивое кодирование);
канал связи – средства передачи сигнала (проводной, беспроводной, оптоволоконный
и т.д.). Может искажать сигнал из-за помех (шум, интерференция, затухание);
- помехи (шум) – внешние или внутренние факторы, вызывающие воздействие сигнала.
Моделируются как случайные процессы (например, битовые ошибки);
декодер – принимает сигнал, восстанавливает сообщение. Можно найти и исправить
ошибку (если использовалось помехоустойчивое кодирование);
- получатель – конечный потребитель информации.
3
36.
2 Помехоустойчивое кодированиеПомехоустойчивое кодирование – это метод передачи данных,
предназначенный для защиты информации от искажений и потерь в процессе
передачи по каналам связи. Суть помехоустойчивого кодирования
заключается в добавлении избыточной информации к исходным данным, что
позволяет обнаруживать и исправлять ошибки, возникшие из-за помех.
Принципы работы помехоустойчивого кодирования. В основе
помехоустойчивого кодирования лежит использование специальных алгоритмов,
которые добавляют к передаваемым данным контрольные биты. Эти биты
позволяют проверять целостность данных и исправлять ошибки. Важные
аспекты включают: избыточность: добавление дополнительной информации
к данным; обнаружение ошибок: выявление ошибок в переданных данных;
коррекция ошибок: исправление обнаруженных ошибок.
1. Понятие корректирующего кода
Теория помехоустойчивого кодирования базируется на результатах
исследований, проведенных Клодом Шенноном. Он сформулировал
теорему для дискретного канала с шумом: при любой скорости передачи
двоичных символов, меньшей, чем пропускная способность канала,
существует такой код, при котором вероятность ошибочного декодирования
будет сколь угодно мала.
4
37.
Построение такого кода достигается ценой введения избыточности – применяя для передачиинформации код, у которого используются не все возможные комбинации, а только некоторые из
них, можно повысить помехоустойчивость приема. Такие коды называют избыточными или
корректирующими. Корректирующие свойства избыточных кодов зависят от правил построения
этих кодов и параметров кода (длительности символов, числа разрядов, избыточности и др.).
В настоящее время наибольшее внимание уделяется двоичным равномерным
корректирующим кодам. Они обладают хорошими корректирующими свойствами и их реализация
сравнительно проста. Наиболее часто применяются блоковые коды. При использовании блоковых
кодов цифровая информация передается в виде отдельных кодовых комбинаций (блоков) равной
длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга, то
есть каждой букве сообщения соответствует блок из п символов. Блоковый код называется
равномерным, если n (значность) остается одинаковой для всех букв сообщения.
Различают разделимые и неразделимые блоковые коды.
При кодировании разделимыми кодами кодовые операции состоят из двух разделяющихся
частей: информационной и проверочной. Информационные и проверочные разряды во всех
кодовых комбинациях разделимого кода занимают одни и те же позиции.
При кодировании неразделимыми кодами разделить символы выходной последовательности
на информационные и проверочные невозможно.
Непрерывными называются такие коды, в которых введение избыточных символов в
кодируемую последовательность информационных символов осуществляется непрерывно, без
разделения ее на независимые блоки. Непрерывные коды также могут быть разделимыми и
неразделимыми.
5
38.
2.2 Общие принципы использования избыточностиСпособность кода обнаруживать и исправлять ошибки
обусловлена наличием избыточных символов. На ввод
кодирующего устройства поступает последовательность из k
информационных двоичных символов. На выходе ей соответствует
последовательность из п двоичных символов, причем n > k. Всего может быть 2 k
различных входных последовательностей и 2 n различных выходных
последовательностей. Из общего числа 2 n выходных последовательностей
только 2 k последовательностей соответствуют входным – называют
разрешенными кодовыми комбинациями. Остальные (2 n – 2 k) возможных
выходных последовательностей для передачи не используются – называют
запрещенными кодовыми комбинациями.
Искажение информации в процессе передачи сводится к тому, что некоторые из
передаточных символов заменяются другими – неверными. Каждая из 2 k разрешенных
комбинаций в результате действия помех может трансформироваться в любую другую.
Всего может быть 2 k · 2 n возможных случаев. В это число входит:
- 2 k случаев безошибочной передачи;
2 k · (2 k – 1) случаев перевода в другие разрешенные комбинации, что
соответствует необнаруживаемым ошибкам;
2 k · (2 n – 2 k) случаев перехода в неразрешенные комбинации, которые
могут быть обнаружены.
6
39.
Часть обнаруживаемых ошибочных кодовых комбинаций от общего числавозможных случаев передачи:
k
2k 2n 2k
2
1 .
Kобн
2k 2n
2n
Рассмотрим обнаруживающую способность кода, каждая комбинация которого содержит
всего один избыточный символ (п = k + 1). Общее число выходных последовательностей
составит 2 k+1, то есть вдвое больше общего числа кодируемых входных последовательностей.
За подмножество разрешенных кодовых комбинаций можно принять, например,
подмножество 2 k комбинаций, содержащих четное число единиц (или нулей). При
кодировании к каждой последовательности из k информационных символов добавляется
один символ (0 или 1), такой, чтобы число единиц в кодовой комбинации было четным.
k
r
n
11011
0 110110
11100
1 111001
Искажение любого четного числа символов переводит разрешенную кодовую
комбинацию в подмножество запрещенных комбинаций, что обнаруживается на приемной
стороне по нечетности числа единиц. Часть обнаруженных ошибок составляет:
2k 1 2k 1 .
Kобн 1 n
2
2k 1 2
7
40.
2.3 Основные параметры корректирующих кодовОсновными параметрами, характеризующими корректирующие свойства
кодов являются избыточность кода, кодовое расстояние, число
обнаруживаемых или исправленных ошибок.
Избыточность корректирующего кода может быть абсолютной и
относительной. Под абсолютной избыточностью понимают число
вводимых дополнительных разрядов r = n – k.
Относительной избыточностью корректирующего кода называют
r n k
k
1 . Эта величина показывает, какую часть общего
величину R
n
n
n
числа символов кодовой комбинации составляют информационные символы.
Ее еще называют относительной скоростью передачи информации.
8
41.
Кодовое расстояние характеризует степень различия любых двухкодовых комбинаций. Оно выражается числом символов, которыми
комбинации отличаются одна от другой.
Кодовое расстояние (расстояние Хэмминга) между двумя битовыми
строками одинаковой длины – это количество позиций, в которых они
различаются:
n
d x, y xi yi , где xi , yi 0,1 .
i 1
Пример: x 10110, y 10011
d x, y 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 2 .
Число
обнаруживаемых
ошибок
определяется
минимальным
расстоянием dmin между кодовыми комбинациями. Это расстояние
называется хэмминговым.
В безызбыточном коде все комбинации являются разрешенными, dmin = 1.
Достаточно только исказиться одному символу, и будет ошибка в
сообщении.
9
42.
Теорема. Чтобы код обладал свойствами обнаруживать одиночныеошибки, необходимо ввести избыточность, которая обеспечивала бы
минимальное расстояние между любыми двумя разрешенными
комбинациями не менее двух: dmin ≥ t0 + 1, где t0 – ошибки кратности.
Доказательство. Возьмем значность кода п = 3. Возможные комбинации натурального
кода образуют следующее множество: 000, 001, 010, 011, 100, 101, 110, 111. Любая
одиночная ошибка трансформирует данную комбинацию в другую разрешенную
комбинацию. Ошибки здесь не обнаруживаются и не исправляются, так как dmin = 1. Если
dmin = 2, то ни одна из разрешенных кодовых комбинаций при одиночной ошибке не
переходит в другую разрешенную комбинацию.
Пусть подмножество разрешенных комбинаций образовано по принципу четности
числа единиц. Тогда подмножества разрешенных и запрещенных комбинаций будут такие:
000, 011, 101, 110 – разрешенные комбинации;
001, 010, 100, 111 – запрещенные комбинации.
Очевидно, что искажение помехой одного разряда (одиночная ошибка) приводит к
переходу комбинации в подмножество запрещенных комбинаций. То есть этот код
обнаруживает все одиночные ошибки.
В общем случае при необходимости обнаруживать ошибки кратности t0 – минимальное
хэммингово расстояние должно быть, по крайней мере, на единицу больше t0, то есть
dmin ≥ t0 + 1.
В этом случае никакая ошибка кратности t0 не в состоянии перевести
одну разрешенную комбинацию в другую.
10
43.
Ошибки можно не только обнаруживать, но и исправлять.Теорема. Для исправления одиночной ошибки каждой разрешенной
кодовой комбинации необходимо сопоставить подмножество запрещенных
кодовых комбинаций. Чтобы эти подмножества не пересекались, хэммингово
расстояние должно быть не менее трех dmin ≥ 2tи + 1, где tи – исправляемые
ошибки кратности.
Доказательство. Пусть п = 3. Примем разрешенные комбинации 000 и 111 (кодовое
расстояние между ними равно 3). Разрешенной комбинации 000 поставим в соответствие
подмножество запрещенных комбинаций 001, 010, 100. Эти запрещенные комбинации
образуются в результате возникновения единичной ошибки в комбинации 000.
Аналогично разрешенной комбинации 111 необходимо поставить в соответствие
подмножество запрещенных комбинаций 110, 011, 101. Если сопоставить эти подмножества
запрещенных комбинаций, то очевидно, что они не пересекаются:
В общем случае исправляемые ошибки кратности tи связаны с кодовым расстоянием
соотношением dmin ≥ 2tи + 1.
11
44.
Для ориентировочного определения необходимой избыточности кодапри заданном кодовом расстоянии d можно воспользоваться верхней
граничной оценкой для r = n – k, называемой оценкой Хэмминга:
tи
r n k log 2 1 Cntи ,
i 1
n!
tи
– сочетание из п элементов по tи.
где Cn
tи ! n tи !
tи
Пример: п = 7, tи = 1, то dmin = 2tи + 1 =3; n k log 2 1 Cntи 3.
i 1
Нужно отметить, что каждый конкретный корректирующий код не
гарантирует исправления любой комбинации ошибок. Коды предназначены
для исправления комбинаций ошибок, наиболее вероятных для заданного
канала связи.
Кодовое расстояние и корректирующая способность
Пусть dmin – минимальное расстояние Хэмминга в коде. Тогда:
- код может обнаруживать до dmin – 1 ошибок;
- код может исправлять до tи dmin 1 2 ошибок.
Пример: Если dmin = 3, то: обнаружение: до dmin – 1 = 2 ошибок; исправление: до
tи 2 2 1 ошибки.
12
45.
2.4 Линейный кодЛинейный код – это код, в котором любая линейная комбинация (по
модулю 2) кодовых слов также является кодовым словом. Работает в
векторном пространстве над полем F2 0,1 (индекс 2 означает, что в этом поле
ровно 2 элемента: 0 и 1). Все кодовые слова образуют линейное
подпространство размерности k в F2n .
Порождающая матрица (G) – матрица размера k × n (k – число
информационных бит; n – длина кодового слова (после кодирования)), строки которой
базисные кодовые слова. Любой информационный вектор u F2k
преобразуется в кодовое слово: c u G mod 2 – ключевая формула в линейном
помехоустойчивом кодировании, и она означает: кодовое слово c получается, как
произведение информационного вектора u (u1, u2 , ..., uk ) , ui 0,1 на порождающую
матрицу G по правилам арифметики по модулю 2. Каждая строка матрицы G – это базисное
кодовое слово, соответствующее одному из базисных информационных векторов (например,
100...0, 010...0 и т.д.). Матрица G определяет, как именно добавляются избыточные
(проверочные) биты. c u G u1 строка 1G u2 строка 2G ... uk строка kG
13
46.
Пример 1: Посчитать c u G mod 2.u (1, 0,1)
1 0 0 1 1 k = 3 – длина исходного сообщения (информационные биты);
G 0 1 0 1 0 , n = 5 – длина закодированного слова (с избыточностью);
То есть, из 3 бит данных получаем 5-битное кодовое слово.
0
1
0
0 1
1 0 0 1 1
c u G (1, 0,1) 0 1 0 1 0 ,
0 0 1 0 1
c u1 (строка 1 G) u2 (строка 2 G) u3 (строка 3 G) 1 строка1 0 строка2 1 строка3 ,
Умножение на 0 дает нулевой вектор: 0⋅(0, 1, 0, 1, 0)=(0, 0, 0, 0, 0).
Умножение на 1 – вектор остается: 1⋅(1, 0, 0, 1, 1)=(1, 0, 0, 1, 1); 1⋅(0, 0, 1, 0, 1)=(0, 0, 1, 0, 1).
c (1, 0, 0,1,1) (0, 0, 0, 0, 0) (0, 0,1, 0,1).
Сначала сложим первые два: (1, 0, 0,1,1) (0, 0, 0, 0, 0) (1, 0, 0,1,1).
Теперь прибавим третий: (1, 0, 0,1,1) (0, 0,1, 0,1) (1, 0,1,1, 0) c (1, 0,1,1, 0).
14
47.
Проверочная матрица (H) – матрица размера (n – k) × n, такая что:G Н T 0 (Н T – транспонированная матрица H размером n × (n – k)).
Используется для проверки, является ли вектор r – кодовым словом: r H T 0
r – кодовое слово, где 0 – нулевая матрица размера k × (n − k), то есть все
элементы равны 0.
Проверим выполнение G Н T 0.
Имеем: G Ik P , где Ik – единичная матрица k × k; P – матрица k × (n – k)
(проверочные биты). Тогда проверочная матрица:
H PT In k
P
.
H
I n k
Т
P
I k P P I n k P P 0 (mod 2).
Теперь умножаем: G Н I k P
I n k
Вывод: G Н T 0.
T
15
48.
Пример 2: Есть порождающая матрица G размером 3×5 (3 строки, 5 столбцов), см. пример 1.1 0 0 1 1
1 0 0
1 1
0 1 0 ; P 1 0 PT 1 1 0
G 0 1 0 1 0 , k = 3, n = 5. G I
1 0 1 .
k P I k
0 1
0 0 1
0 0 1 0 1
1 0 1 0
1 0
1
T
H P I n k , n – k = 2 I 2
H
– проверочная матрица.
0 1
1 0 1 0 1
1 1
1 0
T
H 0 1 .
1 0
0 1
Вычислим произведение R G Н T , G: 3×5; HT: 3×2
1 1
1 0 0 1 1 1 0
T
R G Н 0 1 0 1 0 0 1 Результат: матрица 3×2.
0 0 1 0 1 1 0
0 1
16
49.
R11: 1-я строка G × 1-й столбец HT: 1⋅1+0⋅1+0⋅0+1⋅1+1⋅0=1+0+0+1+0=0 mod 2 R11 = 0R12: 1-я строка × 2-й столбец: 1⋅1+0⋅0+0⋅1+1⋅0+1⋅1=1+0+0+0+1=0 mod 2 R12 = 0
R21: 2-я строка × 1-й столбец: 0⋅1+1⋅1+0⋅0+1⋅1+0⋅0=0+1+0+1+0=0 mod 2 R21 = 0
R22: 2-я строка × 2-й столбец: 0⋅1+1⋅0+0⋅1+1⋅0+0⋅1=0+0+0+0+0=0 mod 2 R22 = 0
R31: 3-я строка × 1-й столбец: 0⋅1+0⋅1+1⋅0+0⋅1+1⋅0=0+0+0+0+0=0 mod 2 R31 = 0
R32: 3-я строка × 2-й столбец: 0⋅1+0⋅0+1⋅1+0⋅0+1⋅1=0+0+1+0+1=0 mod 2 R32 = 0
0 0
Итог: G Н T 0 0 – условие выполнено!
0 0
В примере 1 было рассчитано кодовое слово c (1, 0,1,1, 0) для порождающей матрица G
размером 3×5. Проверим выполнение с H T 0 .
1 1
T
s
с
H
s1, s2
1 0
s1 с столбец 1 H T , s 2 с столбец 2 H T
с H T (1, 0, 1,1, 0) 0 1 s1 = 1⋅1+0⋅1+1⋅0+1⋅1+0⋅0=1+0+0+1+0=0 mod 2 ⇒ s1 = 0
1 0 s2 = 1⋅1+0⋅0+1⋅1+1⋅0+0⋅1=1+0+1+0+0=0 mod 2 ⇒ s2 = 0
s с H T 0, 0 → ошибок нет, это корректное кодовое слово.
0 1
17
50.
Синдром ( s ) – это вектор, который помогает определить, была лиошибка при передаче кодового слова, и, при правильной настройке, где
именно эта ошибка произошла. Он вычисляется на стороне приемника
(получателя) и используется для обнаружения и исправления ошибок без
необходимости переспрашивать отправителя.
При получении вектора r (возможно, с ошибками), вычисляется
синдром: s r H T .
Если s 0 , ошибок нет. Если s 0 , значит, есть ошибки.
Пример 3: Принятый вектор (после передачи): r (1,1, 0,1,1). Он не является корректным
кодовым словом – в нем есть ошибка (например, из-за помех).
Поскольку r – строка длины 5, а HT – матрица 5×2, результат
1 1
будет вектор-строка длины 2: s r H T s1, s 2
1 0
s1 r столбец 1 H T , s 2 r столбец 2 H T
s r H T (1,1, 0, 1,1) 0 1 s1 = 1⋅1+1⋅1+0⋅0+1⋅1+1⋅0=1+1+0+1+0=1 mod 2 ⇒ s1 = 1
s2 = 1⋅1+1⋅0+0⋅1+1⋅0+1⋅1=1+0+0+0+1=0 mod 2 ⇒ s2 = 0
1
0
s с H T 1, 0 – не нулевой вектор, значит: в принятом слове
0 1
r (1,1, 0,1,1) есть ошибка.
Синдром (1,0) указывает на ошибку во 2-й позиции (102 = 210, если есть таблица
синдромов). Значит, нужно инвертировать 2-й бит в r : r (1,1, 0,1,1)
инвертируем
(1, 0, 0,1,1).
18
51.
2.5 Групповой код с проверкой на четностьГрупповой код с проверкой на четность – это линейный двоичный код,
в котором:
каждое кодовое слово имеет четное число единиц (или, в
альтернативной версии – нечетное);
- добавляется один контрольный бит (бит четности) к исходным данным,
чтобы общее количество единиц в слове стало четным (или нечетным).
Такой код является групповым, потому что множество всех кодовых
слов образует группу по сложению по модулю 2.
Основные понятия.
1)
Проверка на четность. Цель: обнаружить одиночные ошибки (и
любое нечетное число ошибок).
Правило: сумма всех бит в кодовом слове по модулю 2 должна быть
равна 0 (для четной четности) или 1 (для нечетной).
Обычно используется четная четность: c1 c2 ... cn 0 (mod 2)
2) Структура кода. Пусть у нас есть k информационных бит. Тогда:
- длина кодового слова: n = k + 1;
- добавляется 1 бит четности, получаем (k + 1, k)-код
Пример 1: (8,7)-код – 7 информационных бит + 1 бит четности
19
52.
Как строится кодовое слово?Алгоритм:
- берем информационное слово длины k: u (u1, u2 , ..., uk );
- вычисляем сумму бит по модулю 2 ( – операция сложения по модулю 2,
или XOR (исключающее ИЛИ)): p u1 u2 ... uk – это ключевая формула в
кодировании с проверкой на четность. Она определяет, как вычисляется бит четности p по
исходным информационным битам u1, u2 , ..., uk .
- добавляем бит p, при этом бит p выбирается так, чтобы:
u1 u2 ... uk p 0 (mod 2) → получаем кодовое слово: c (u1, u2 , ..., uk , p),
теперь общее число единиц в c – четное.
Пример 1: Построение кодового слова
Пусть u (1, 0,1,1) – 4 информационных бита. Сумма: 1+0+1+1=3≡1(mod 2). Бит
четности: p = 1. Кодовое слово: с (1, 0,1,1,1) – проверка: число единиц = 4 → четное.
Пусть u (1,1, 0, 0) – 4 информационных бита. Сумма: 1+1+0+0=2≡0(mod2). Бит
четности: p = 0. Кодовое слово: с (1,1, 0, 0, 0) – проверка: число единиц = 2 → четное.
20
53.
Как обнаруживаются ошибки?На приемной стороне проверяется, сохраняется ли четность:
s c1 c2 ... cn .
Если s = 0 → ошибок не обнаружено, если s = 1 → обнаружена ошибка
(нечетное число ошибок).
Важно: код обнаруживает, но не исправляет ошибки.
Пример 2: Обнаружение одиночной ошибки
Передано: с (1, 0,1,1,1). При получении: r (1,1,1,1,1) – ошибка во 2-м бите (0 → 1).
Проверка: s 1 1 1 1 1 5 mod 2 1. Синдром s = 1 → ошибка обнаружена.
2.6 Коды с постоянным весом
Весом называется число единиц, содержащихся в кодовых
комбинациях. Если число единиц во всех комбинациях кода будет
постоянным, то такой код будет кодом с постоянным весом. Коды с
постоянным весом относятся к классу блочных неразделимых кодов,
поскольку здесь невозможно выделить информационные и проверочные
символы. Наибольшее применение получили коды «3 из 7», «3 из 8», хотя
возможны другие варианты. Первая цифра указывает на вес кода, вторая –
на общее число символов в комбинации.
21
54.
Разрешенными комбинациями кода «3 из 7» являются такие, которые содержат триединицы независимо от их места в комбинации, например 1110000 или 1010100 и т.д.
Обнаружение ошибок сводится к определению их веса. Если вес отличается от заданного,
то считается, что произошла ошибка. Код обнаруживает веса ошибок нечетной кратности
и части ошибок четной кратности. Не обнаруживаются ошибки, при которых несколько
единиц превращается в нули и столько же нулей – в единицы (ошибки смещения), так как
при этом вес кода не изменяется.
Пусть c (c1, c2 , ..., cn ) – двоичное слово. Вес Хэмминга (c) – это число
единиц в этом слове. Если для всех кодовых слов кода выполняется:
(c) const – то такой код называется кодом с постоянным весом .
Пример:Рассмотрим код длины 4 и весом 2:
Кодовое слово Вес (число единиц)
Кодовое слово Вес (число единиц)
1)
1100
2
4)
0110
2
2)
1010
2
5)
0101
2
3)
1001
2
6)
0011
2
Все слова имеют ровно две единицы → это код с постоянным весом 2 длины 4. Такой
код обозначается как (n, M, ), где: n – длина слова; M – число кодовых слов; – вес.
В этом примере: (4, 6, 2)-код.
Коды с постоянным весом используются в ситуациях, где физический
канал требует стабильной средней мощности сигнала или устойчивого
тактирования.
22
55.
2.7 Код ХэммингаКод Хэмминга – один из первых и самых важных примеров
помехоустойчивого кодирования, разработанный Ричардом Хэммингом в
1950 году. Он позволяет обнаруживать и исправлять одиночные ошибки в
передаваемых данных, что делает его незаменимым в системах хранения и
передачи информации. Код Хэмминга является линейным, двоичным,
групповым кодом с минимальным расстоянием dmin = 3, что дает ему
способность исправлять одну ошибку на слово: (n, k)-код, где: n 2r 1 –
длина кодового слова; k 2r 1 r – число информационных бит; r n k –
число проверочных бит.
Пример:r = 3 ⇒ n = 7, k = 4 → (7, 4)-код Хэмминга.
Код Хэмминга добавляет к информационным битам проверочные биты
(биты четности), расположенные на позициях степеней двойки: 1, 2, 4, 8, 16,
... Остальные позиции – информационные биты.
Каждый проверочный бит контролирует определенные позиции в кодовом
слове, определяемые двоичным представлением номера позиции.
23
56.
Рассмотрим (7,4)-код Хэмминга:Позиция: 1
2
3
4
5
6
7
Бит:
p1
p2
d1
p3
d2
d3
d4
где: p1, p2, p3 – проверочные биты (на позициях, равных степеням двойки: 1, 2, 4
(20), (21), (22)); d1, d2, d3, d4 – информационные биты (на остальных позициях).
Каждый проверочный бит pi отвечает за все позиции, номер которых в
двоичной записи имеет 1 на i-м месте: p1 контролирует позиции: 1,3,5,7;
p2 – 2,3,6,7; p3 – 4,5,6,7.
Разберем это максимально понятно.
Для определения, какие именно позиции контролирует проверочный бит pi нужно
посмотреть на двоичную запись номера позиции и проверить, стоит ли там 1 на i-м месте.
Позиция
(десятичная)
1
2
3
4
5
6
7
Двоичная
запись (3 бита)
001
010
011
100
101
110
111
Бит 3 (старший)
p3
0
0
0
1
1
1
1
Бит 2 (средний) Бит 1 (младший)
p2
p1
0
1
1
0
1
1
0
0
0
1
1
0
1
1
24
57.
Вычисление проверочных битПравило: сумма всех бит в контролируемой группе по модулю 2 равна 0
(четная четность) – условие четности.
Пусть информационные биты: d1 d2 d3 d4 = 1 0 1 1
Позиция: 1
2
3
4
5
6
7
p1
p2
d1
p3
d2
d3
d4
Бит:
?
?
1
?
0
1
1
Вычисляем p1 (контролирует позиции: 1, 3, 5, 7 → p1, d1, d2, d4):
p1 d1 d2 d4 0 ⇒ p1 d1 d2 d4 1 0 1 0.
Вычисляем p2 (контролирует: 2, 3, 6, 7 → p2, d1, d3, d4):
p2 d1 d3 d4 0 ⇒ p2 d1 d3 d4 1 1 1 1.
Вычисляем p3 (контролирует: 4, 5, 6, 7 → p3, d2, d3, d4):
p3 d2 d3 d4 0 ⇒ p3 d2 d3 d4 0 1 1 0.
Формирование кодового слова
Позиция: 1
2
3
4
5
6
7
p1
p2
d1
p3
d2
d3
d4
Бит:
0
1
1
0
0
1
1
Кодовое слово: 0 1 1 0 0 1 1
25
58.
Декодирование и исправление ошибокПредположим, при передаче возникла ошибка в 5-й позиции:
Вместо 0 1 1 0 0 1 1 принято 0 1 1 0 1 1 1 (вместо 0 стало 1).
Вычисляем синдром: синдром – это результат проверок четности.
Каждый бит синдрома соответствует одной проверке.
Позиция
1
2
3
4
5
6
7
Бит
p1 = 0
p2 = 1
d1 = 1
p3 =0
d2 = 1
d3 = 1
d4 = 1
Бит синдрома s1: проверка группы p1 – позиции: 1, 3, 5, 7 → биты: 0, 1, 1, 1:
s1 0 1 1 1 1.
Бит синдрома s2: проверка группы p2 – позиции: 2, 3, 6,7 → биты: 1, 1, 1, 1:
s2 1 1 1 1 0.
Бит синдрома s3: проверка группы p3 – позиции: 4, 5, 6,7 → биты: 0, 1, 1, 1:
s3 0 1 1 1 1.
Синдром: s1s2 s3 10 12 510 – синдром равен номеру позиции с ошибкой!
Ошибка в 5-й позиции → инвертируем 5-й бит: 1 → 0, получаем: 0 1 1 0 0 1 1.
Преимущества кода Хэмминга: простота реализации; эффективно исправляет одиночные
ошибки; минимальная избыточность для такой задачи; линейная структура позволяет
использовать матрицы; широко применяется в памяти (RAM, ECC), процессорах, сетях.
Ограничения: не исправляет двойные ошибки; может ошибочно «исправить» двойную
ошибку, превратив ее в тройную; эффективность падает при высоком уровне шума.
26
59.
2.8 Циклические кодыЦиклические коды – важный класс линейных помехоустойчивых кодов,
в которых циклический сдвиг любого кодового слова также является
кодовым словом. Это свойство позволяет эффективно реализовывать
кодирование и декодирование с помощью полиномиальной арифметики и
регистров сдвига.
Циклические коды – это линейный (n, k)-код, обладающий свойством:
если c (c0 , c1, ..., cn 1 ) – кодовое слово, то его циклический сдвиг
(cn 1, c0 , c1, ..., cn 2 ) – тоже кодовое слово.
Пример 1: Если 1011000 – кодовое слово, то 0101100, 0010110, 0001011 и т.д. – тоже
должны быть кодовыми словами.
Чтобы было удобно работать с циклическими сдвигами нужно каждое
двоичное слово длины n представить как полином степени меньше n:
c(x) c c x c x2 ..., c xn 1.
0
1
2
n 1
Пример 2: Слово (1, 0, 1, 1) → полином: c(x) 1 0 x 1 x2 1 x3 1 x2 x3 .
27
60.
Пусть c(x) c0 c1 x c2 x2 ..., c n 1 xn 1, циклический сдвиг влево:c0 c1 ... cn 1 c1 с2 ... cn 1 c0 .
В полиномах это соответствует: x c(x) mod (x n 1), т.е. при умножении на х:
x xn 1 xn , значит xn «переходит» в x0 1. Это как «закольцевание» –
последний бит становится первым.
В линейном коде все кодовые слова – это линейные комбинации базисных
слов. В циклическом коде – еще сильнее: все кодовые слова – это кратные
одного полинома g(x), называемого порождающим полиномом. То есть
c(x) u(x) g(x) mod 2, где u(x) – информационный полином (степени < k).
В циклическом коде существует порождающий полином g(x), такой что:
g(x) делитель xn – 1 в кольце:
- код имеет длину n, значит, все полиномы степени < n;
- циклический сдвиг c(x) → x⋅c(x) mod(xn − 1);
- чтобы результат оставался в коде, он должен делиться на g(x).
Но если c(x) делится на g(x), то и x⋅c(x) делится на g(x), только если g(x)
делитель xn – 1 в кольце. Это необходимое и достаточное условие для того,
чтобы множество всех кратных g(x) образовывало циклический код длины n.
28
61.
Кодирование: алгоритм (систематический код):1) Исходное сообщение: u(x) (степень < k).
2) Умножаем на xr: xr u(x).
3)
Делим xr u(x) на порождающий полином g(x), получаем остаток r(x),
который станет проверочными битами.
4) Кодовое слово: c(x) xr u(x) r(x).
Теперь c(x) делится на g(x), и информационные биты стоят в старших
позициях.
Пример 3: (7,4)-код (аналог кода Хэмминга)
Пусть: n = 7, k = 4, r = 3; g(x) = 1 + x + x3.
1) u(x) = 1 + x2 + x3 → сообщение: 1 0 1 1.
2) x3 u(x) = x3 + x5 + x6
3)
Делим x3 u(x) = x3 + x5 + x6 на g(x) = x3 + x + 1 для нахождения остатка r(x) и
построения кодового слова c(x) x3 u(x) r(x), чтобы оно делилось на g(x).
Запишем полиномы в порядке убывания степеней:
делимое: x6 + x5 + 0x4 + x3 + 0x2 + 0x + 0; делитель: x3 + 0x2 + x + 1
Шаг 1: Делим старшие члены (старший член делимого: x6; старший член делителя: x3): x6 / x3 = x3.
Умножаем делитель на x3: x3⋅(x3 + x + 1)=x6 + x4 + x3.
Вычитаем это из делимого (по модулю 2, вычитание = XOR):
(x6 + x5 + 0x4 + x3) – (x6 + 0x5 + x4 + x3) = x5 + x4. Остаток: x5 + x4.
29
62.
Шаг 2: x5 / x3 = x2.Умножаем делитель на x2: x2⋅(x3 + x + 1)=x5 + x3 + x2.
Вычитаем (по модулю 2, вычитание = XOR):
(x5 + x4 + 0x3 + 0x2) – (x5 + 0x4 + x3 + x2) = x4 + x3 + x2. Остаток: x4 + x3 + x2.
Шаг 3: x4 / x3 = x.
Умножаем делитель на x: x⋅(x3 + x + 1) = x4 + x2 + x.
Вычитаем (по модулю 2, вычитание = XOR):
(x4 + x3 + x2 + 0х) – (x4 + 0x3 + x2 + x) = x3 + 0x2 + x. Остаток: x3 + x.
Шаг 4: x3 / x3 = 1.
Умножаем делитель на 1: 1⋅(x3 + x + 1) = x3 + x + 1.
Вычитаем (по модулю 2, вычитание = XOR):
(x3 + 0x2 + х + 0) – (x3 + 0x2 + x + 1) = 1. Окончательный остаток: r(x) = 1.
ИТОГ: делимое: x6 + x5 + x3; делитель: x3 + x + 1; остаток: r(x) = 1.
Кодовое слово: c(x) x3 u(x) r(x) (x6 x5 x3 ) 1 x6 x5 x3 1.
Коэффициенты: x6: 1; x5: 1; x4: 0; x3: 1; x2: 0; x1: 0; x0: 1 → 1 1 0 1 0 0 1
30
63.
2.9 Код БЧХКод БЧХ (Боуза – Чоудхури – Хоквингема) – это циклический код,
способный исправлять заранее заданное число ошибок t.
Особенность: можно спроектировать код, который исправляет ровно t
ошибок, выбрав подходящий порождающий полином.
Параметры кода БЧХ.
Длина: n = 2m − 1 (неприводимый случай), где m – это параметр,
определяющий размер конечного поля, в котором строится код БЧХ.
Число исправляемых ошибок: t.
Число проверочных бит: r ≤ mt.
Число информационных бит: k = n – r.
Минимальное расстояние: dmin ≥ 2t + 1.
Построение порождающего полинома
Пусть – примитивный элемент поля F2m . Тогда порождающий полином
g(x) – это наименьшее общее кратное (НОК) минимальных полиномов
степеней , 2, …, 2t: g(x) НОК(m1 (x), m2 (x), ..., m2t (x)), где mi (x) –
минимальный полином для i.
31
64.
Пример: (15,7)-код БЧХ, t = 2n = 15 – длина кодового слова (в битах); k = 7 – число информационных бит; r = n – k = 8
– число проверочных бит; t = 2 – код может исправить до 2 ошибок.
Такой код имеет скорость R = k/n = 7/15 ≈ 0,467, что означает почти 50 % избыточности
– но зато он устойчив к двум ошибкам.
n = 2m – 1 m = 4, работаем в конечном поле F16 F24 .
Построение поля F16 F24 . Чтобы строить код, нужно расширить двоичное поле F2 0,1
до поля из 16 элементов. Для этого выбираем примитивный неприводимый (не делится на x,
x + 1, x2 + x + 1) полином степени 4: p(x) = 1 + x + x4. Его корень порождает все ненулевые
элементы: 0, 1, 2, …, 14 – все ненулевые элементы поля, т.е. 15 = 1, k ≠ 1 при k = 1, 2,
…,14. Значит, 14 – это максимальная степень, при которой k ≠ 1, и это порядок
мультипликативной группы поля, 14 – это предпоследний элемент в цикле, и 14 = –1, потому
1
что 14 = 15 = 1, т.е. 14 1.
Свойство: 4 1 (из p( ) = 0). Это правило позволяет выражать все степени n через
полиномы степени ≤ 3: b c 2 d 3 , a, b, c, d F 2.
Построение порождающего полинома g(x). Порождающий полином g(x) должен иметь
корни: 0, 1, 2, 1 (всего 2t = 4 подряд идущих степеней ).
Найдем минимальные полиномы:
1) Для : m1 (x) 1 x x4 (это наш p(x)).
32
65.
2) Для 2: В характеристике 2: ( )2 2 , и если m ( ) 0, то m ( 2 ) 0 m (x) m (x).1
1
2
1
2
3
4
3
3) Для : m (x) 1 x x x x ,
3
4
4
4) Для : 1 , и он принадлежит тому же полю → его минимальный полином m (x) .
1
Порождающий полином: g(x) НОК(m1 (x), m2 (x), m3 (x), m4 (x)) m1(x) m3 (x).
g(x) (1 x x4 ) (1 x x2 x3 x4 )
1 (1 x x2 x3 x4 ) x (1 x x2 x3 x4 ) x4 (1 x x2 x3 x4 )
(1 x x2 x3 x4 ) (x x2 x3 x4 x5 ) (x 4 x5 x6 x7 x8 ) 1 x4 x6 x7 x8 .
Складываем по модулю 2
Степень Сумма коэффициентов Результат
1
1
x0
x1
1+1=0
0
x2
1+1=0
0
x3
1+1=0
0
x4
1+1+1=1
1
x5
1+1=0
0
1
1
x6
x7
1
1
x8
1
1
g(x) 1 x4 x6 x7 x8 . Степень g(x) 8 – порождающий полином степени 8 r = 8
проверочных бит k = n – r = 15 – 8 = 7 (15, 7)-код БЧХ.
33
66.
Почему он исправляет t = 2 ошибки? t = 2 dmin ≥ 2t + 1 = 2 2 + 1=5, значит, кодd 1
должен иметь dmin ≥ 5, чтобы исправлять до 2 ошибок: t min
2 ; обнаруживать до 4
2
ошибок.
Как происходит кодирование?
Пусть информационное слово: u = (u0, u1, …, u6) → полином u(x) степени ≤ 6.
Алгоритм (систематический код):
1) умножаем на x8: x8 u(x);
2) делим x8 u(x) на g(x), получаем остаток r(x) степени < 8;
3) кодовое слово: c(x) = x8u(x) + r(x).
Теперь c(x) делится на g(x), и информационные биты – в старших 7 позициях.
Пусть u(x) 1 x2 x3 x6 → сообщение: 1 0 1 1 0 0 1.
1) x8 u(x) x8 (1 x2 x3 x6 ) x8 x10 x11 x14 .
2) запишем полиномы x8 u(x) x8 x10 x11 x14 и g(x) 1 x4 x6 x7 x8 в порядке
убывания степеней: x8 u(x) x14 x11 x10 x8 ; g(x) x8 x7 x6 x4 1 и поделим один
полином на другой.
34
67.
Делимое: x8 u(x) x14 x11 x10 x8 .Делитель: g(x) x8 x7 x6 x4 1.
Шаг 1: Делим старшие члены (старший член делимого:x14; старшийчлен делителя: x8): x14 / x8 = x6.
Умножаем делитель на x6: x6 (x8 + x7 + x6 + x4 + 1) = x14 + x13 + x12 + x10 + x6.
Вычитаем это из делимого (по модулю 2, вычитание = XOR):
(x14 + x11 + x10 + x8) – x14 + x13 + x12 + x10 + x6 = x13 + x12 + x11 + x8 + x6.
Остаток: x13 + x12 + x11 + x8 + x6.
Шаг 2: x13 / x8 = x5.
Умножаем делитель на x5: x5 (x8 + x7 + x6 + x4 + 1) = x13 + x12 + x11 + x9 + x5.
Вычитаем это из делимого (по модулю 2, вычитание = XOR):
(x13 + x12 + x11 + x8 + x6) – x13 + x12 + x11 + x9 + x5 = x9 + x8 + x6 + x5.
Остаток: x9 + x8 + x6 + x5.
Шаг 3: x9 / x8 = x.
Умножаем делитель на x: x (x8 + x7 + x6 + x4 + 1) = x9 + x8 + x7 + x5 + x.
Вычитаем это из делимого (по модулю 2, вычитание = XOR):
(x9 + x8 + x6 + x5) – x9 + x8 + x7 + x5 + x = x7 + x6 + x.
Остаток: x7 + x6 + x.
Шаг 4: x7 / x8 = x–1 – степень меньше 1 → деление завершено.
r(x) = x7 + x6 + x или в коэффициентах (степени от x0 до x7):
r(x) = 0 +x + 0x2 + 0x3 + 0x4 + 0x5 + x6 + x7 r(x) = x + x6 + x7.
35
68.
Формируем кодовое словоc(x) x8 u(x) r(x) (x14 x11 x10 x8 ) (x7 x6 x) x14 x11 x10 x8 x7 x6 x .
Теперь запишем все коэффициенты от x14 до x0:
x14
x13
x12
x11
x10
x9
x8
x7
x6
x5
x4
x3
x2
x1
x0
1
0
0
1
1
0
1
1
1
0
0
0
0
1
0
данные
Проверочные биты
Кодовое слово: 1 0 0 1 1 0 1 1 1 0 0 0 0 1 0
Проверка: делится ли c(x) на g(x)?
По построению – да, потому что: c(x) x8 u(x) r(x) и r(x) x8 u(x) mod g(x)
c(x) 0 mod g(x)
Условие циклического кода выполнено.
Спасибо за внимание
36
69.
ДИСКРЕТНАЯ МАТЕМАТИКАРТУ МИРЭА
Фроленкова Лариса Юрьевна
70.
Лекция 11 Алгебра чиселАрифметика остатков. НОД. Алгоритм Евклида. Диофантовы
уравнения. Китайская теорема об остатках. Символы Лежандра и
Якоби. Парадокс дней рождений. Простые числа. Тесты на
простоту чисел. Генерация простых чисел
2
71.
1 Арифметика остатковЦелые числа и основы теории делимости
Целые числа – это натуральные числа (положительные числа для счета), их
отрицательные аналоги и ноль. Множество целых чисел обозначается буквой Z и включает
в себя ..., -3, -2, -1, 0, 1, 2, 3, ... Целые числа не имеют дробной части и используются в
различных вычислениях, включая случаи, когда результат меньше нуля.
Целое число a делится на целое число b ≠ 0, если существует целое число
q такое, что a = b ∙ q.
Обозначение: b|a (произносят: «b делит a»). Данная
запись
содержит в себе предположение, что b ≠ 0.
Укажем простейшие свойства делимости:
1) любое целое a|a (а ≠ 0) – рефлексивность;
2) если b|a и a|c, то b|c – транзитивность;
3) если b|a, то при любом сочетании знаков ±b|±a;
4) если b|a и b|c, то b|(a ± c);
5) если b|a и с ≠ 0, то bс|aс;
6) если b|a и с Z – произвольное, то b|aс;
7) если b|a и a ≠ 0, то |b| ≤ |a|;
8) если b|a и a|b, то a ≠ ±b.
3
72.
Теорема (о делении с остатком). Для любых целых чисел a и b (b ≠ 0)существует и единственна пара целых чисел q и r, которые называют
частным и остатком от деления a на b таких, что: a bq r , 0 r b .
Частный случай: r = 0 b|a.
Пример 1:
1) Пусть a = – 1234, b = 23. Представим число a в виде: –10 = 7∙q + r или
10
r
q
7
7
10
10
q 2 – целая часть числа –10 = 7∙(–2) + 4, 0 4 7 , q 2, r = 4.
7
7
10
r
10
10
q q 1 – целая часть числа
2) Разделим 10 на 7: 10 = 7∙q + r или
7
7
7
7
10 = 7∙(1) + 3, 0 3 7 , q 1, r = 3.
Говорят, что целые числа a и b сравнимы по модулю m, если они дают
одинаковый остаток при делении на m: a ≡ b (mod m) ⟺ m∣(a − b)
Пример 2: 17 ≡ 5 (mod 6), так как 17 – 5 = 12, а 6∣12.
Множество всех чисел, сравнимых с a по модулю m, называется классом
вычетов по модулю m. Всего таких классов – m: {0, 1, 2, ..., m – 1}.
Пример 3: при m = 5: Z5 = {[0], [1], [2], [3], [4]}
Операции в Zm
4
73.
Можно складывать и умножать классы:[a] + [b] = [a + b mod m];
[a]⋅[b] = [a⋅b mod m].
Пример 3: [3] + [4] = [7 mod 5] = [2] в Z5.
2 Наибольший общий делитель чисел. Алгоритм Евклида.
Наименьшее общее кратное чисел.
Пусть a1, a2, …, an – целые числа. Общим делителем (ОД) данных чисел
называется любое целое число d, делящее каждое из этих чисел, т.е. d|a1, d|a2,
…, d|an.
Наибольшим общим делителем (НОД) чисел a1, a2, …, an называется
наибольшее положительное число, делящее каждое из этих чисел.
Наибольший общий делитель чисел a1, a2, …, an, делится на любой другой их
общий делитель.
Пример 1: Есть числа: 6, 9, 15 ОД(6, 9, 15) = (± 1, ± 3) НОД(6, 9, 15) = 3.
Если среди чисел a1, a2, …, an есть не равное нулю, то множество общих
делителей этих чисел конечно.
5
74.
Теорема. Для любых, отличных от нуля чисел a1, a2,…, an выполняетсяравенство: НОД(a1, a2,…, an) = НОД(НОД(a1, a2,…, an – 1), an).
Таким образом, наибольший общий делитель n чисел (n 3) можно найти,
найдя сначала наибольший общий делитель n – 1 чисел: d' = НОД(a1, a2,…, an– 1), а
затем найти наибольший общий делитель от полученного таким образом
числа d' и последнего числа an: d =НОД(d', an)
Пример 2: Есть числа 12, 18, 24. d' = НОД(12, 18) = 6; d = НОД(6, 24) = 6.
Как находить НОД?
Способ 1: Разложение на простые множители: ОД – это произведение
общих простых множителей, взятых с наименьшим показателем степени.
Пример 3: Есть числа a = 72, b = 60.
a = 72 = 23 ⋅ 32, b = 60 = 22 ⋅ 31 ⋅ 51
Общие множители: 2min(3,2) = 22; 3min(2,1) = 31. НОД(72, 60) = 22 ⋅ 31 = 4 ⋅ 3=12.
6
75.
Способ 2: Алгоритм Евклида (рекомендуется для больших чисел).Алгоритм Евклида базируется на теоремах, в которых все
рассматриваемые величины предполагаются целыми.
Теорема 1. Если a целое число, b – натуральное и b|a, то множество общих
делителей чисел a и b совпадает с множеством делителей b. В частности, (a, b) = b.
Теорема 2. Если a = bq + r, 0 ≤ r < b, то (a, b) = (b, r).
Положим r0 = a, r1 = b и обозначим r2, ..., rn – последующие делители в
алгоритме Евклида.
Тогда r1 = b. Таким образом, получаются следующие равенства:
a = r0 = bq1 + r2,
0 ≤ r2 < b,
0 ≤ r3 < r2,
b = r1 = r2q2 + r3,
0 ≤ r4 < r3,
r2 = r3q3 + r4,
…………,
…………….
0 ≤ rn < rn – 1,
rn – 2 = rn – 1qn – 1 + rn,
rn – 1 = rnqn.
Последний остаток rn + 1 = 0. Алгоритм останавливается, когда деление
произойдет без остатка.
(a, b) = (b, r2) = (r2, r3) = (r3, r4) = · · · = (rn – 1, rn) = (rn, 0) = rn.
Таким образом, наибольший общий делитель равен последнему делителю (он же
последний ненулевой остаток) в алгоритме Евклида.
7
76.
Пример 4: Найти наибольший общий делитель чисел 3009 и 894.Пользуясь алгоритмом Евклида, находим
3009 = 894 3 + 327, 894 = 327 2 + 240, 327 = 240 1 + 87, 240 = 87 2 + 66,
87 = 66 1 + 21, 66 = 21 3 + 3, 21 = 3 7 + 0.
Последний ненулевой остаток равен 3, поэтому (3009, 894) = 3.
Для реализации алгоритма Евклида на компьютере больше подходит следующая его
форма, в которой отсутствуют индексы у делителей и остатков.
Теорема 3. Количество делений, необходимое для вычисления с
помощью алгоритма Евклида наибольшего общего делителя двух
положительных целых чисел, не превышает пятикратного количества
цифр в десятичной записи меньшего из этих двух чисел.
8
77.
Алгоритм (Обобщенный алгоритм Евклида).Дано: Совокупность целых неотрицательных чисел {a1, ..., an}.
Найти: Наибольший общий делитель d = (a1, ..., an).
1.
Заменить список {a1, ..., an}, переставив его элементы так, чтобы число,
стоящее на первом месте, было наименьшим из положительных чисел списка.
2. Если все числа a2, ..., an равны нулю, положить d = a1, СТОП.
3.
Заменить в списке {a1, ..., an} каждое из ненулевых чисел a2, ..., an его
остатком при делении на a1. Перейти в пункт 1 алгоритма.
Чтобы показать, как работает этот алгоритм рассмотрим пример.
Пример 5: Вычислить d = (10, 6, 15, 24).
Имеем D = (6, 10, 15, 24) = [10 mod 6 = 4; 15 mod 6 = 3; 24 mod 6 = 0] = (6, 4, 3, 0) =
= (3, 6, 4, 0) = (3, 0, 1, 0) = (1, 3, 0, 0) = (1, 0, 0, 0) = 1, т.е. числа 10, 6, 15, 24 взаимно просты.
9
78.
Пусть a1, a2, …, an – ненулевые целые числа. Целое число m называетсяобщим кратным чисел a1, a2, …, an, если оно кратно каждому из этих чисел,
то есть m делится на каждое из этих чисел без остатка: a1|m; a2|m; …; an|m.
Среди всех общих кратных есть наименьшее положительное – оно
называется наименьшее общее кратное (НОК).
Все общие кратные двух чисел – это кратные их НОК. То есть: если
m = НОК(a, b), то общие кратные: m, 2m, 3m, 4m, …
Пример 6: Есть числа (4, 6).
Кратные 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, …
Кратные 6: 6, 12, 18, 24, 30, 36, …
Общие кратные: 12, 24, 36, 48, … – то есть любое число, делящееся и на 4, и на 6
НОК(4, 6) = 12
Как найти НОК?
Способ 1: Через разложение на простые множители.
Правило: НОК – это произведение всех простых множителей, входящих
в числа, с наибольшим показателем степени.
Пример 7: a = 12 = 22 ⋅ 31; b = 18 = 21 ⋅ 32.
Берем: 2max(2,1) = 22; 3max(1,2) = 32. НОК(12,18) = 22 ⋅ 32 = 4 ⋅ 9 = 36 – общие кратные: 36, 72,
108, 144, …
10
79.
Способ 2: Через НОДa b
.
НОК(а,b)
d a,b
12 18
216
36.
d 12,18 6
Примеры для закрепления
Пример 7: НОК(12,18)
a
b
НОД(a, b)
НОК(a, b)
Проверка: НОД НОК
8
12
4
24
4⋅24=96=8⋅12✅
15
25
5
75
5⋅75=375=15⋅25✅
11
1 (взаимно просты)
77
1⋅77=77=7⋅11✅
Свойства НОД и НОК
Свойство
Формула
Коммутативность
d(a, b) = d(b, a), НОК(a, b) = НОК(b, a)
Ассоциативность
d(a, d(b, c)) = d(d(a, b), c)
d(a, b) = a, НОК(a, b) = b
Если a∣b, то
Взаимно простые числа
d(a, b) = 1 ⇒ НОК(a, b) = a⋅b
НОК для нескольких чисел
НОК(a, b, c) = НОК(НОК(a, b), c)
НОД для нескольких чисел
НОД(a, b, c) = НОД(НОД(a, b), c)
7
11
80.
Простые и составные числаНатуральное число n > 1 называется простым, если оно делится только
лишь на себя и на единицу. Числа 1 и n называются тривиальными
делителями натурального числа n.
Натуральное число n > 1 называется составным, если его можно
представить в виде произведения двух меньших натуральных чисел.
Заметим, что оба множителя при этом отличны от 1. Таким образом,
составное число n можно представить в виде: n = n1 n2, где 1 < n1 < n и
1 < n2 < n. Пример 8: 23 47 = 1081.
Множество натуральных чисел разбивается на три подмножества:
1) простые числа; 2) составные числа; 3) единица.
Основная теорема арифметики: всякое целое число, отличное от 0 и
± 1 имеет, и притом единственное, представление в виде произведения
простых множителей. Пример 9: 70 = 2 5 7.
Каноническим разложением целого числа a называется представление
a в виде a n 1 n 2 ... n k , где n1, n2, …, nk – попарно различные простые
1
2
k
числа; 1, 2, …, k – натуральные числа.
12
81.
Пример 10: n = 2088, 2088 = 23 32 29 – каноническое разложение числа 20882088 2
1044 2
522 2
261 3
87 3
29 29
Сравнения целых чисел и их свойства
Целые числа a и b называются сравнимыми по модулю m, если разность
a – b делится на m, т.е. если m|(a – b), обозначение: a ≡ b (mod m).
Натуральное число m называют модулем сравнения, числа a и b
соответственно левой и правой частями сравнения. Согласно определению
сравнение a ≡ 0 (mod m) означает, что a делится на m.
Пример 11: 157 ≡ 4 (mod 3); 74 ≡ 4 (mod 5).
13
82.
Критерий сравнимости: целое число a сравнимо с целым числом b помодулю m тогда и только тогда, когда у них одинаковые остатки при делении на m.
Целые числа a и b называются сравнимыми по модулю m, если остатки от
деления этих чисел на m равны.
Свойства сравнений
1.
Каждое целое число сравнимо с самим собой по любому модулю
(рефлексивность или закон тождества): a ≡ a.
2. Части сравнения можно менять местами (симметричность): если a ≡ b,
то b ≡ a.
3.
Числа, сравнимые с одним и тем же числом, сравнимы между собой по
данному модулю (транзитивность): если a ≡ b и b ≡ c, то a ≡ c.
Любое целое число сравнимо со своим остатком от деления на модуль:
a ≡ r (mod m).
4.
Сравнения по одному и тому же модулю можно почленно складывать:
если a ≡ b (mod m) и c ≡ d (mod m), то a + c ≡ b + d (mod m).
5.
Части сравнения можно делить на их общий делитель, взаимно простой
с модулем: если a ≡ b (mod m), то a/d ≡ b/d (mod m), где (d, m) = 1.
Пример 11: 14 ≡ 4 (mod 5), (2, 5) = 1 7 ≡ 2 (mod 5).
14
83.
6. Если a ≡ b (mod m) и d|a, d|b, d|m, то a/d ≡ b/d (mod m/d).7. Если a ≡ b (mod m1), a ≡ b (mod m2), … , a ≡ b (mod mn), то a ≡ b (mod m), где
m = [m1, m2,…, mn].
8. Если a ≡ b (mod m) и d|a, d|m, то d|b.
3 Диофантовы уравнения
Диофантово уравнение – это уравнение, решение которого ищется в
целых числах. Наиболее распространенный вид – линейное уравнение:
ax + by = c
где a, b, c – целые коэффициенты; x, y – целочисленные неизвестные.
Уравнение имеет решение тогда и только тогда, когда d(a, b)∣c
Если это условие выполнено, решений бесконечно много.
Метод решения: расширенный алгоритм Евклида
1) Найдем d = НОД(a, b) и коэффициенты x0, y0, такие что: ax0 +by0 = d
c
c
c
2) Умножим решение на : x* x0 , y* y0
d
d
d
b
a
3) Общее решение: x x * t , y y * t , t Z.
d
d
15
84.
Пример: 15x + 9y = 6Цель – найти целые числа x0 и y0, такие что: 15x0 + 9y0 = d(15, 9), а мы знаем, что
d(15, 9) = 3, так, что ищем: 15x0 + 9y0 = 3.
Шаг 1: Обычный алгоритм Евклида (нахождение НОД)
Сначала найдем d(15, 9), деля «уголком»:
15 = 1 ⋅ 9 + 6 → остаток 6
9 = 1 ⋅ 6 + 3 → остаток 3
6 = 2 ⋅ 3 + 0 → остаток 0, значит, d = 3
Теперь «идем назад» – от последнего ненулевого остатка (то есть от 3).
Шаг 2: Обратный ход (расширенный алгоритм Евклида)
Возьмем предпоследнее равенство (остаток 3): 3 = 9 – 1 ⋅ 6 (уравнение A)
Но у нас есть остаток 6 – его можно выразить из первого равенства:
6 = 15 − 1 ⋅ 9(из: 15 = 1 ⋅ 9 + 6) (уравнение B)
Теперь подставим уравнение B в уравнение A: 3 = 9 − 1 ⋅ (15 − 1 ⋅ 9)
Раскроем скобки: 3 = 9 − 1 ⋅ 15 + 1 ⋅ 9 или 3 = − 1 ⋅ 15 + 2 ⋅ 9
✅ Вот она – искомая комбинация!
Шаг 3: Интерпретация результата
У нас получилось: 3 = ( − 1) ⋅ 15 + 2 ⋅ 9
Перепишем в виде: 15 ⋅ ( − 1) + 9 ⋅ 2 = 3
Сравни с общим видом: 15x0 + 9y0 = 3, где a = 15 , b = 9 , d = 3
Значит: x0 = − 1, y0 = 2
Это – частное решение однородного уравнения 15x + 9y = 3
16
85.
Шаг 4: Почему это важно?Мы хотим решить уравнение: 15x + 9y = 6
Но у нас есть: 15 ⋅ ( − 1) + 9 ⋅ 2 = 3
c 6
Умножим обе части на
2: 15 ⋅ ( − 2) + 9 ⋅ 4 = 6 → получаем частное решение
d 3
исходного уравнения: x∗ = − 2, y∗ = 4
А общее решение (с параметром t): x = − 2 + 3t, y = 4 − 5t, t Z (где 3 = 9/d = 9/3,
5 = 15/d = 15/3).
4 Китайская теорема об остатках (КТО)
Если модули m1, m2, …, mk попарно взаимно просты, то система
сравнений:
x a1 (mod m1 )
x a (mod m )
2
2
.
– имеет единственное решение по модулю M m1m2 mk .
.
.
x ak (mod mk )
17
86.
Алгоритм решения1) M m1m2 mk
2) M i M mi
3) yi M i 1 mod mi
k
Решение: x ai M i yi mod M
i 1
Пример: Нужно найти такое целое число x, которое одновременно удовлетворяет трем
условиям:
x 2 (mod 3)
x 3 (mod 5) .
x 2 (mod 7)
Это означает: при делении x на 3 – остаток 2; при делении x на 5 – остаток 3; при
делении x на 7 – остаток 2. И мы хотим найти одно число x, которое выполняет все три
условия сразу.
Шаг 1: Проверка условий КТО
Китайская теорема об остатках работает, если модули попарно взаимно просты.
Модули: 3, 5, 7: d(3, 5) = 1; d(3, 7) = 1; d(5, 7) = 1
✅ Все модули – попарно взаимно просты, значит, КТО применима.
➜
⬛ Существует единственное решение по модулю: M = 3 ⋅ 5 ⋅ 7 = 105, То есть, все
решения будут вида: x ≡ X(mod 105), где X – какое-то число от 0 до 104.
18
87.
Шаг 2: Обозначим компонентыОбозначим: m1 = 3, a1 = 2; m2 = 5, a2 = 3; m3 = 7, a3 = 2; M = 105
Теперь вычислим вспомогательные величины.
Шаг 3: Вычисляем M i M mi .
M1 M m1 105 3 35; M 2 M m2 105 5 21; M 3 M m3 105 7 15.
Шаг 4: Находим обратные по модулю – y i M i 1 mod mi
Нам нужно найти такие числа yi, что: M i yi 1 mod mi
y1 35 1 mod 3. Сначала упростим 35 mod 3: 35 ÷ 3 = 11 ⋅ 3 = 33, 35 – 33 = 2 ⇒ 35 ≡ 2 (mod 3).
Теперь ищем y1, такое что: 2 ⋅ y1 ≡ 1 (mod 3):
2 ⋅ 1 = 2 ≡ 2 mod 3 – нет; 2 ⋅ 2 = 4 ≡ 1 mod 3 – ✅ → y1 = 2.
y2 21 1 mod 5 21 mod 5 = 1, потому что 21 = 4 ⋅ 5 + 1 ⇒ 1 ≡ 1 (mod 5).
Ищем y2, такое что: 1 ⋅ y2 ≡ 1 (mod 5) ⇒ y2 = 1 → y2 = 1.
y3 15 1 mod 7 15 mod 7 = 1, потому что 15 = 2 ⋅ 7 + 1 ⇒ 1 ≡ 1 (mod 7).
Ищем y3, такое что: 1 ⋅ y3 ≡ 1(mod 7) y3 = 1 → y3 = 1.
Шаг 5: Вычисляем решение
Формула: x (a1M1 y1 a2 M 2 y2 a 3M3 y3 ) mod M
Подставим: x (2 35 2 3 21 1 2 15 1) mod 105 → x = 233 mod 105
140
63
30
233
105 ⋅ 2 = 210, 233 − 210 = 23 x = 23. ✅ Ответ: x ≡ 23 (mod 105).
19
88.
Шаг 6: ПроверкаПроверим, выполняются ли все три условия:
1) x ≡ 2 (mod 3) → 23 ÷ 3 = 7 ⋅ 3 = 21, 23 − 21 = 2 23 ≡ 2(mod 3) ✅
2) x ≡ 3 (mod 5) → 23 ÷ 5 = 4 ⋅ 5 = 20, 23 − 20 = 3 23 ≡ 3(mod 5) ✅
3) x ≡ 2 (mod 7) → 23 ÷ 7 = 3 ⋅ 7 = 21, 23 − 21 = 2 23 ≡ 2(mod 7) ✅
ВСЕ СХОДИТСЯ!
5 Символы Лежандра и Якоби
a
Символ Лежандра , где a – целое число; p – нечетное простое число.
p
Символ Лежандра – это функция, которая помогает определить,
является ли число a квадратом по модулю простого p. Говоря проще: можно
ли найти такое целое число x, чтобы x2 ≡ a (mod p)?
Если да – a называется квадратичным вычетом по модулю p. Если
нет – квадратичным невычетом. Символ Лежандра как раз и говорит нам,
к какой категории относится a .
20
89.
Определение символа Лежандра1,
если x2 a (mod p) имеет решение и
a не делится на p квадратичный вычет по модулю по p
a
2
p 1, если нельзя найти целое число x, чтобы x a (mod p) невычет
0
если a 0 (mod p)
Как понять, что «a – квадрат по модулю p»?
Это значит: существует такое целое x, что x2 ≡ a (mod p)
Пример 1: p = 7
Шаг 1: Что значит «квадрат по модулю 7»?
Когда мы говорим «квадрат по модулю 7», мы имеем в виду: x2 mod 7 – то есть, остаток
от деления x2 на 7, например: если x =3 , то x2 = 9, а 9 mod 7 = 2; если x = 4 , то 16 mod 7 = 2.
Таким образом, мы смотрим: какие остатки могут быть у квадратов чисел при делении на 7?
21
90.
Шаг 2: Переберем все остатки по модулю 7Поскольку мы работаем по модулю 7, достаточно проверить числа от 0 до 6 – потому
что любое целое число дает один из этих остатков при делении на 7. Посчитаем x2 mod 7
для x = 0, 1, 2, 3, 4, 5, 6:
x
x2 mod 7
Пояснение
0
0 mod 7 = 0
0
1
1 mod 7 = 1
1
2
4 mod 7 = 4
4
3
9 mod 7 = 2
9 – 7 = 2 – остаток 9 2 (mod 7)
4
16 mod 7 = 2
14 = 2 7, 16 – 14 = 2 – остаток 16 2 (mod 7)
5
25 mod 7 = 4
21 = 3 7, 25 – 21 = 4 – остаток 25 4 (mod 7)
6
36 mod 7 = 1
35 = 5 7, 36 – 35 = 1 – остаток 36 1 (mod 7)
Шаг 3: Соберем все результаты
Выпишем все значения x2 mod 7: x = 0 → 0; x = 1 → 1; x = 2 → 4; x = 3 → 2; x = 4 → 2;
x = 5 → 4; x = 6 → 1. То есть, получили последовательность: 0, 1, 4, 2, 2, 4, 1 (в этом списке
нет 3, 5, 6). Теперь выберем уникальные значения – то есть, какие разные остатки вообще
могут быть у квадратов:
0 – особый случай (делится на 7);
1, 2, 4 – квадратичные вычеты по модулю 7;
3, 5, 6 – квадратичные невычеты. Мы не получили 3, 5, 6, то есть нет такого целого x,
чтобы: x2 ≡ 3 (mod 7); x2 ≡ 5 (mod 7); x2 ≡ 6 (mod 7) → эти числа не являются квадратами
по модулю 7.
22
91.
Теперь найдем символы Лежандра a p для разных значений a, где p = 7 – простое число:a
a p
0
0
1
1
2
1
3 -1 (нет x, чтобы x2 ≡ 3)
4
1
5 -1 (нет x, чтобы x2 ≡ 5)
6 -1 (нет x, чтобы x2 ≡ 6)
Символ Якоби a n – это обобщение символа Лежандра на случай, когда
n – не простое число, а нечетное составное число.
k1
r
a
a
k1
k2
kr
Если n p1 p2 pr , то .
n i 1 pi
Символ Якоби – формальный объект, определяемый через разложение n
на простые множители. Пусть n – нечетное натуральное число (например,
n = 15, 45, 105). Тогда его можно разложить на простые: n pk11 pk22 pkrr .
Пример 2: n = 45 = 32 ⋅ 51, где: p1 = 3, k1 = 2; p2 = 5, k2 = 1.
23
92.
aa
Разберем, что означает каждая часть :
n i 1 pi
Обозначение
Что означает
a n
Символ Якоби – то, что мы вычисляем
n
Составное нечетное число (например, 45)
pi
i-й простой множитель в разложении n
ki
степень, с которой pi входит в n
a pi
символ Лежандра по модулю pi
r
k1
r
произведение по всем простым множителям
i 1
a p i
k
i
символ Лежандра возводится в степень ki
Пример 3: вычислим a n 2 45
Разложим 45 = 32 ⋅ 51. Тогда: a n 2 45 2 3 2 2 5 1.
Вычислим символы Лежандра:
- 2 3 : Рассмотрим модуль p = 3. Числа по модулю 3: 0, 1, 2.
24
93.
Найдем квадраты по модулю 3.x x2
x2 mod 3
Результат Возможные квадраты: 0 и 1. Обычно 0
исключаем, если a ≡ 0. Единственный
0 0 0 mod 3 = 0 02 ≡ 0 (mod 3)
0
ненулевой квадратичный вычет по модулю 3
1 1 1 mod 3 = 1 12 ≡ 1 (mod 3)
1
– это 1. Число 2 не является квадратом ни для
какого целого x по модулю 3. 2 3 1,
2 4 4 mod 3 = 1 22 ≡ 1 (mod 3)
1
2 при делении на 3 дает остаток, не равный
нулю, поэтому не 0, а именно –1.
- 2 5 : Рассмотрим модуль p = 5. Числа по модулю 5: 0, 1, 2, 3, 4.
Найдем квадраты по модулю 3.
x x2
x2 mod 3
Результат
0 0 0 mod 5 = 0 02 ≡ 0 (mod 5)
0
Возможные ненулевые квадраты: 1, 4. То есть
квадратичные вычеты по модулю 5: {1, 4}.
1 1 1 mod 5 = 1 12 ≡ 1 (mod 5)
1
Число 2 не является квадратом ни для какого
2 4 4 mod 5 = 1 22 ≡ 4 (mod 5)
4
целого x по модулю 5 2 5 1.
3 9 9 mod 5 = 4 32 ≡ 4 (mod 5)
4
4 16 16 mod 5 = 1 42 ≡ 1 (mod 5)
1
Сводная таблица
Модуль а
Квадраты(вычеты)
а в списке?
a p
3
2 {0, 1} → ненулевые: {1}
нет
-1
5
2 {0, 1, 4} → ненулевые: {1, 4}
нет
-1
(a n) (2 45) (2 3)2 (2 5)1 ( 1)2 ( 1) 1.
25
94.
ı . Важное предупреждение!Символ Якоби не означает, что a – квадрат по модулю n, даже если он равен 1.
Пример 3: 2 15 1, но уравнение x2 ≡ 2 (mod 15) не имеет решений!
15 = 3 ⋅ 5 2 3 1; 2 5 1 2 15 ( 1) ( 1) 1.
Но так как 2 – невычет по модулю 3, то x2 ≡ 2 (mod 15) не может иметь решения.
– Вывод:
−
Если a n 1, то a – точно не квадрат по модулю n.
Если a n 1, то a может быть квадратом, а может и не быть – нужна
дополнительная проверка.
6 Парадокс дней рождения
Парадокс дней рождения – утверждение, состоящее в том, что в группе,
состоящей из 23 или более человек, вероятность совпадения дней рождения
(число и месяц) хотя бы у двух людей превышает 50 %.
k 1
i
, P(k) – вероятность совпадения дней рождения
P(k) 1 1
365
i 0
хотя бы у двух человек в группе из k человек (i = 0 → первый человек).
26
95.
Пример 1: k = 22
i
1 0 1 1 1 1 364 1 0, 274 % .
P(2) 1 1
1
365
365 365
365 365
i 0
✅ Логично: у второго человека 1 шанс из 365 совпасть с первым.
Пример 2: k = 23 i
0
1
22
P(23) 1
22
.
1 1
1
1 0, 4927 0,5073 50 %
1
1
365
365 365 365
i 0
− То есть, в группе из 23 человек вероятность совпадения дней рождения уже больше 50%!
–
0
1
49
Пример 3: k = 50 i
P(50) 1
.
49
1 1
1
1 0,0296
1
1
365
365 365 365
i 0
Пример 4: k = 70 i
0 1 69
P(70) 1
.
69
1 1
1
99 %
1
1
365
365 365 365
i 0
0,9704
97 %
27
96.
7 Тесты на простоту чиселПеребор делителей
Проверить, делится ли n на любое число от 2 до n .
Если у числа n нет делителей (кроме 1 и самого себя) в диапазоне от 2 до
n , то оно простое.
Пример 1: n = 29 – является ли оно простым?
Вычислим 29 5,385. Значит, проверяем делители от 2 до 5: d = 2, 3, 4, 5.
Проверяем: 29 ÷ 2 = 14,5 → не делится; 29 ÷ 3 ≈ 9,67 → не делится; 29 ÷ 4 = 7,25 → не делится;
29 ÷ 5 = 5,8 → не делится. ✅ Ни одно d ∈ [2, 5] не делит 29 без остатка 29 – простое число.
Пример 2: n = 35 – является ли оно простым?
Вычислим 35 5,916 . Значит, проверяем делители от 2 до 5: d = 2, 3, 4, 5.
Проверяем: 35 ÷ 2 = 17,5 → не делится; 35 ÷ 3 ≈ 11,667 → не делится; 35 ÷ 4 = 8.75 → не
делится; 35 ÷ 5 = 7 → делится. ✅ d∣35 35 – составное число.
28
97.
Метод ФермаВ компьютерных приложениях, требующих больших простых чисел обычно проверяют, не
является ли случайно выбранное число простым с помощью подходящих критериев. Одним из
таких критериев служит метод выделения множителей Ферма: целое нечетное число n не
является простым тогда и только тогда, когда существуют неотрицательные числа p и q, такие что
p2 – q2 = n и при этом p – q > 1. Очевидно, если p2 – q2 = n, то n = (p – q)(p + q), то есть n не простое
число. Применение этого метода заключается в попытке найти целые числа p и q, такие, что:
p2 = n + q2. При это полагаем q = 1, 2, 3,… до тех пор, пока n + q2 не станет полным
квадратом. Если до значения q = (n – 1)/2 полный квадрат не будет достигнут, то n – простое число.
q2 = p2 – n. При этом берем в качестве m наименьшее целое число такое, что m2 ≥ n,
и последовательно полагаем p = m, m + 1, … до тех пор, пока p2 – n не станет полным
квадратом. Так как q не может превысить значения (n – 1)/2, то проверку продолжаем до
значения p = (n + 1)/2. Если полный квадрат не достигнут, значит n – простое число.
Тест Ферма: Если число n нечетное и составное, то его можно
представить как разность квадратов: n = a2 − b2 = (a − b)(a + b).
Алгоритм:
1) Начинаем с a n – потолок числа – наименьшее число, которое
больше или равно n , например 17 4,123 5.
2) Вычисляем b2 = a2 – n.
3) Если b2 – полный квадрат, то n = (a − b)(a + b).
29
98.
Пример 3.Проверяем число 15: 15 3,87 ⇒ a = 4; a2 − n = 16 − 15 = 1 = 12 ⇒ b = 1
Тогда 15 = (4 − 1)(4 + 1) = 3 ⋅ 5 – составное.
Проверяем число 17: 17 4,12 ⇒ a = 5; a2 − n = 25 − 17 = 8 – не квадрат;
a = 6 ⇒ 36 − 17 = 19 – не квадрат; a = 7 ⇒ 49 − 17 = 32 – не квадрат;
a = 8 ⇒ 64 − 17 = 47 – не квадрат; a = 9 ⇒ 81 − 17 = 64 = 82 – квадрат.
Получили b = 8, но тогда: 17 = (9 − 8)(9 + 8) = 1 ⋅ 17. Это тривиальное (с участием
единицы и самого числа) разложение → 17 – простое.
Важно: Метод Ферма эффективен, когда множители близки друг к другу. Для простых
чисел он не дает нетривиального разложения.
Тест Соловея – Штрассена
Основан на критериях Эйлера и символа Якоби. Для нечетного целого
n > 2 и случайного a ∈ {2, 3, ..., n – 2}, взаимно простого с n, выполняется:
если n – простое, то a(n – 1)/2 (a/n) (mod n), где (a/n) – символ Якоби
(обобщение символа Лежандра):
(a 1)(n 1)
a a
– для нечетных простых a и n;
1 4
n n
30
99.
0, если n | aa
n 1, если а квадратичный вычет по модулю n .
1, если а квадратичный невычет по модулю n
Если это сравнение нарушено, то n – точно составное. Если
выполняется – n возможно простое (но может быть и составным – тогда a
называется ложным свидетелем).


























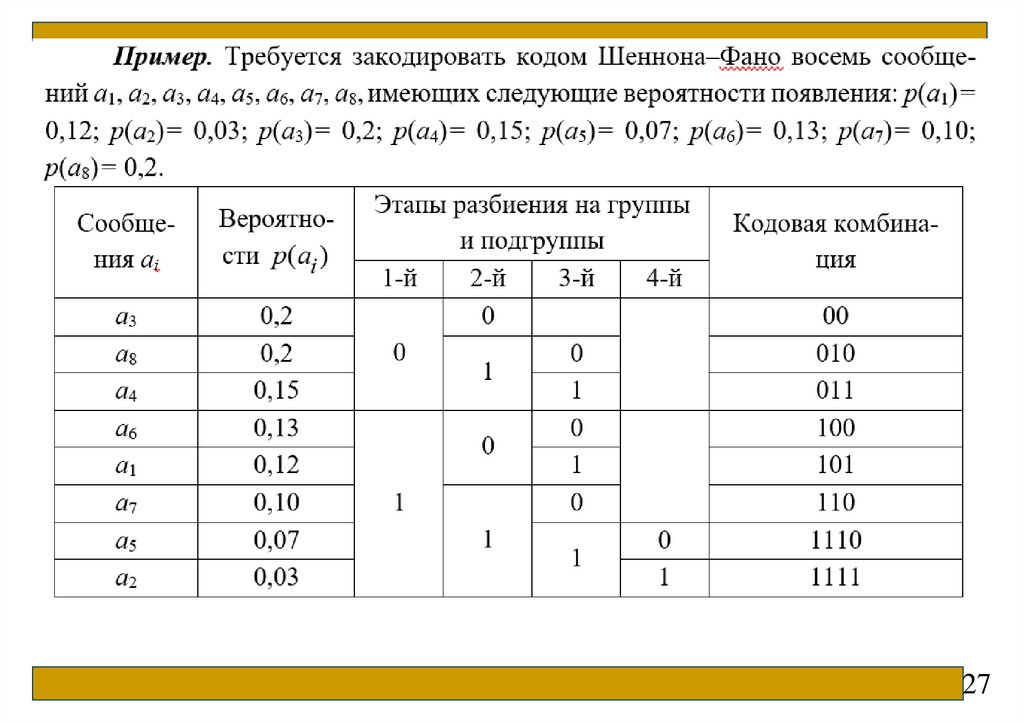


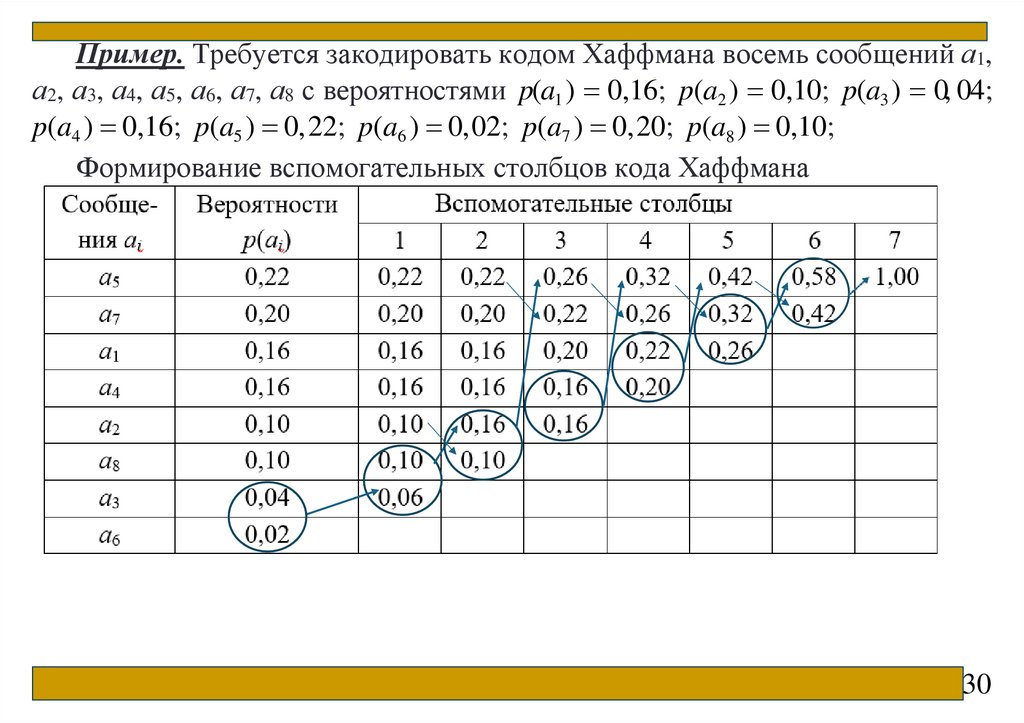
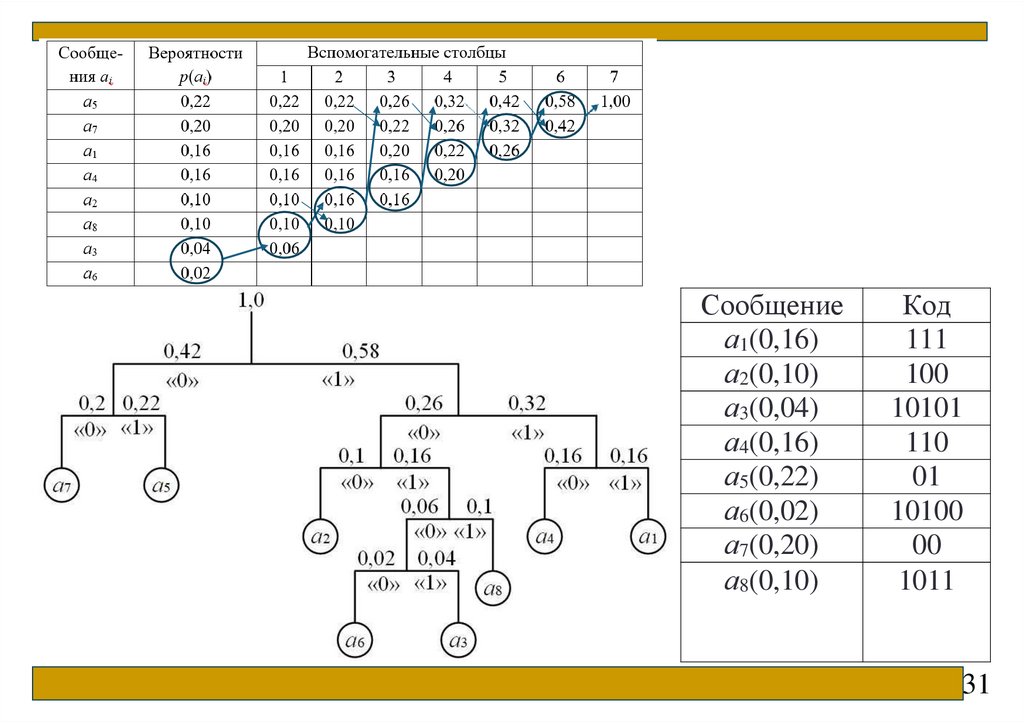
























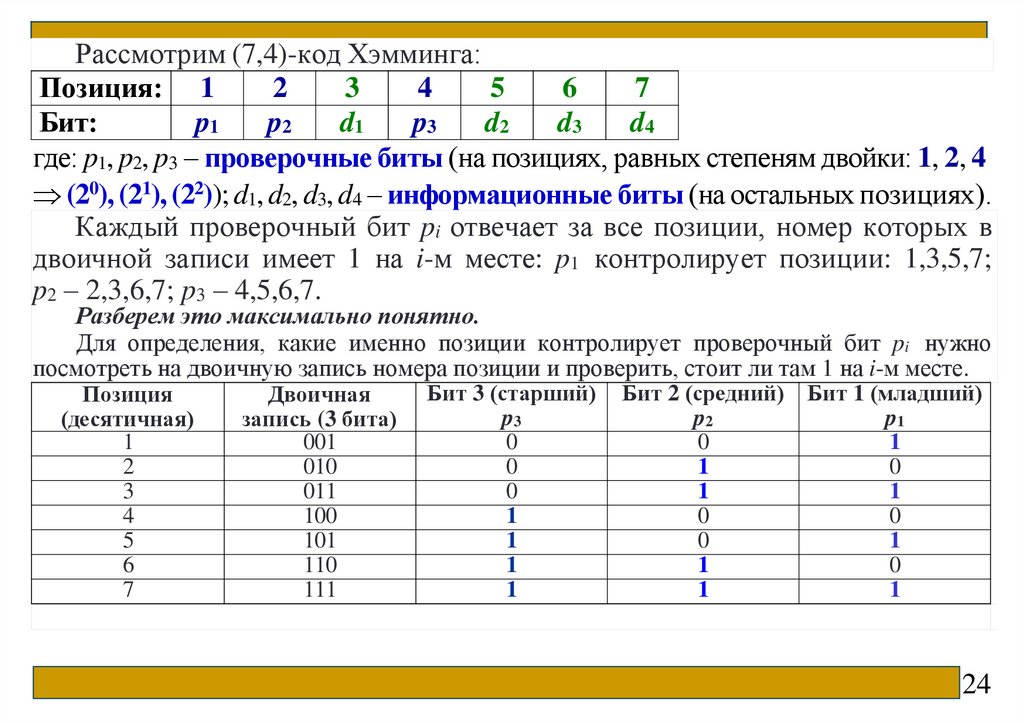











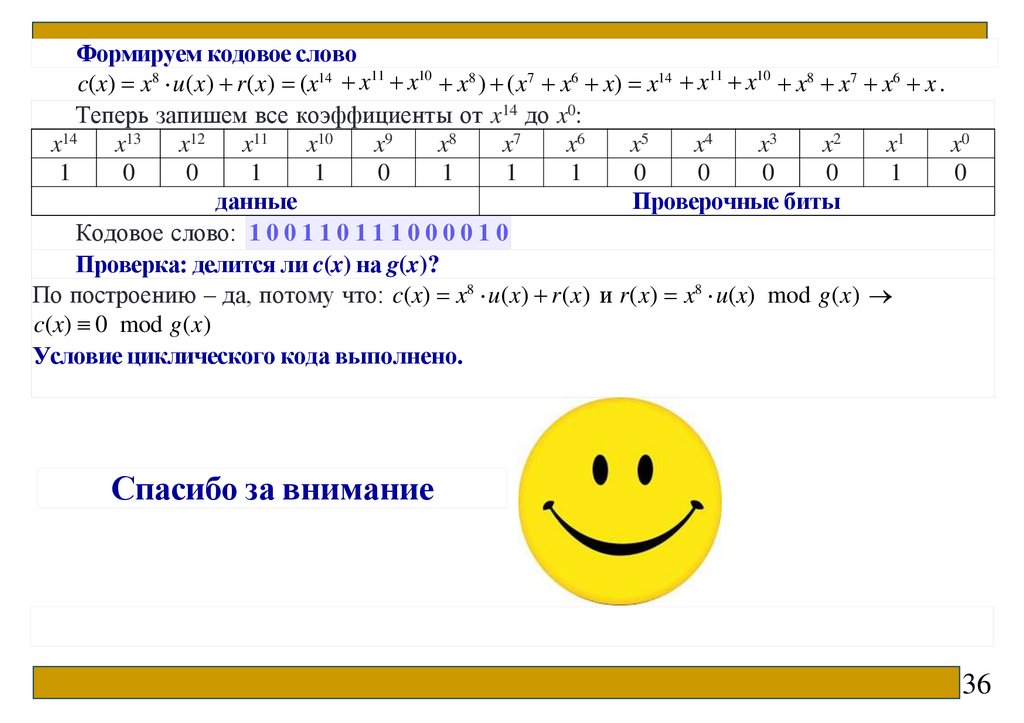


















































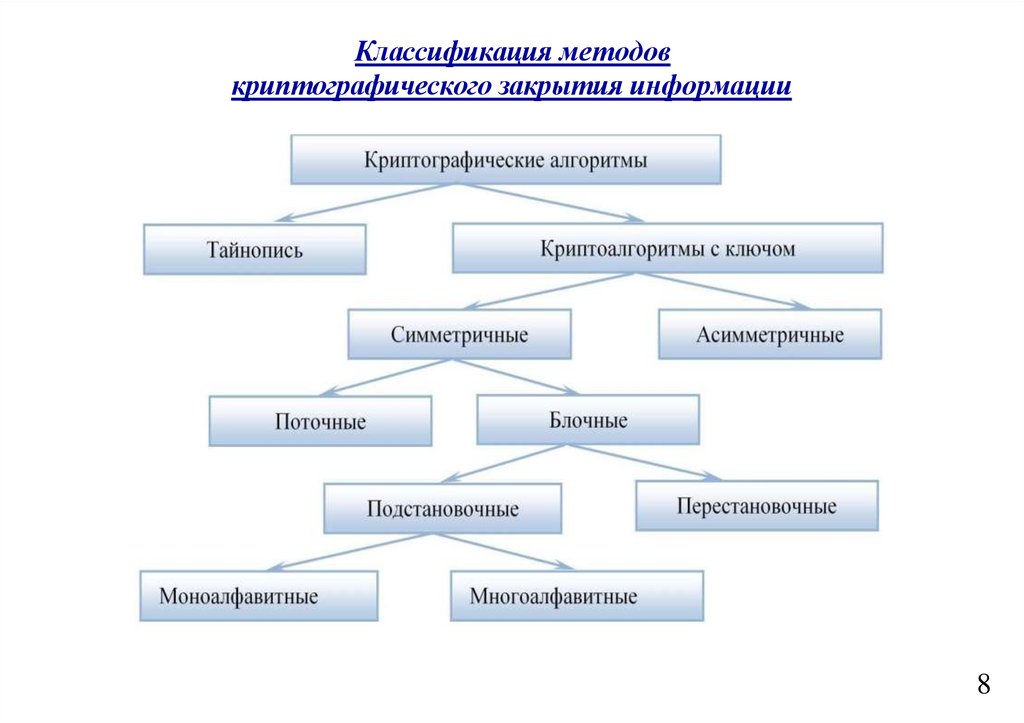
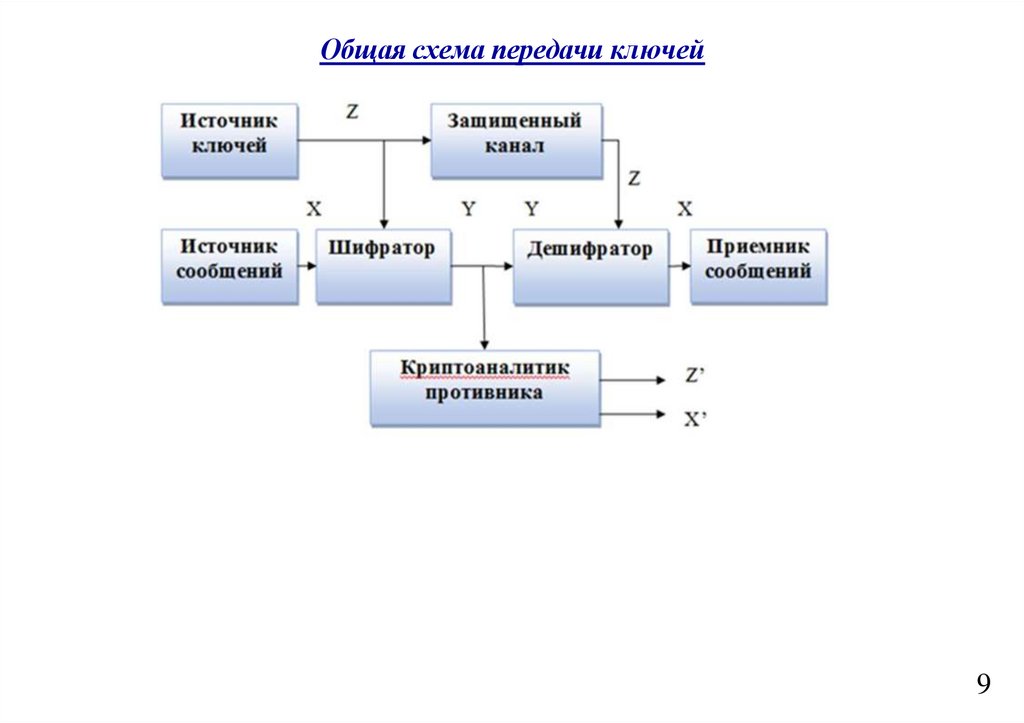
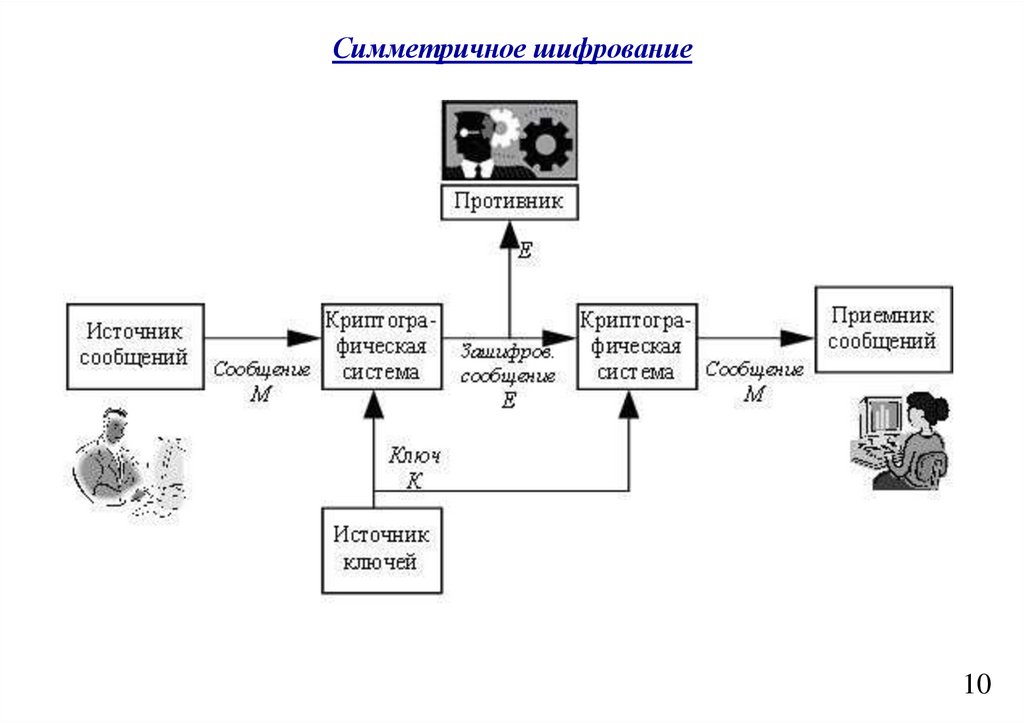

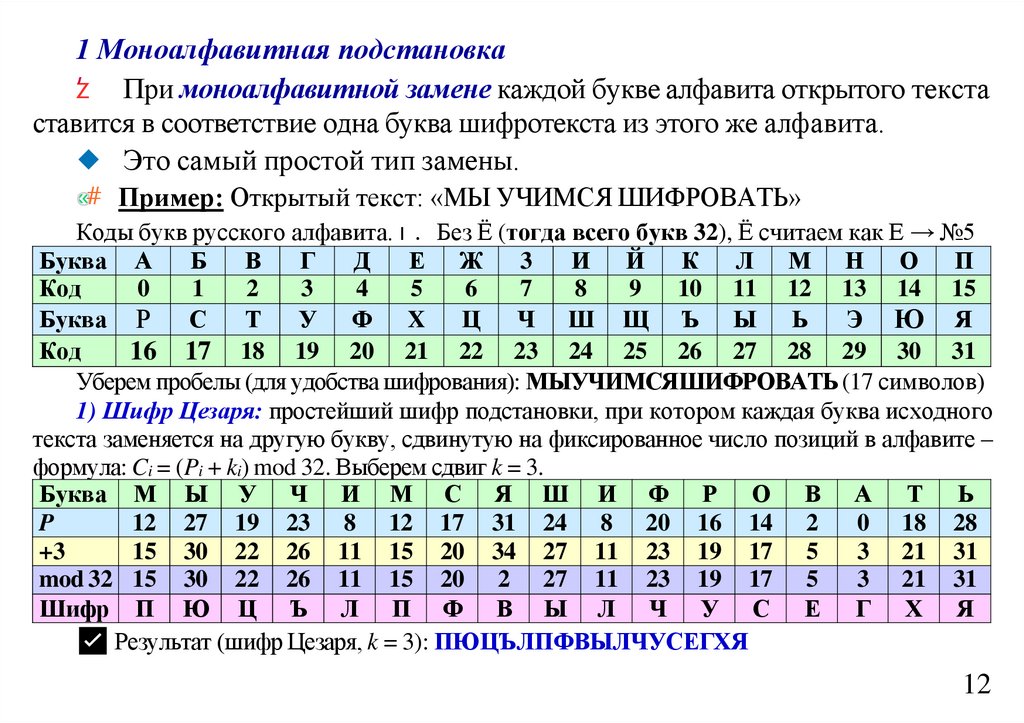
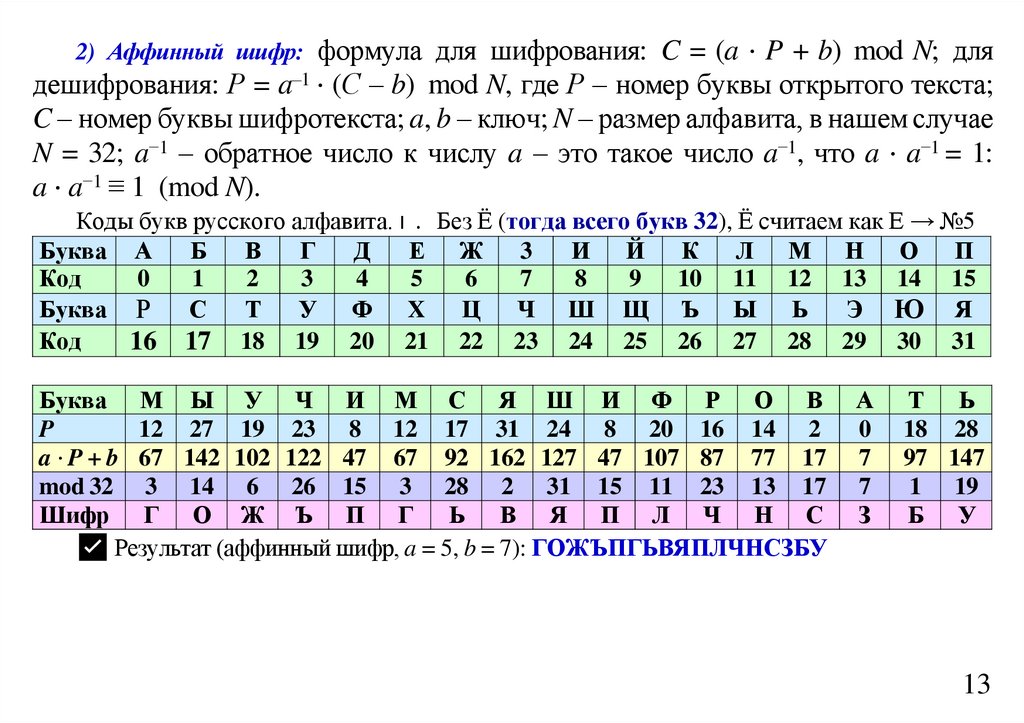
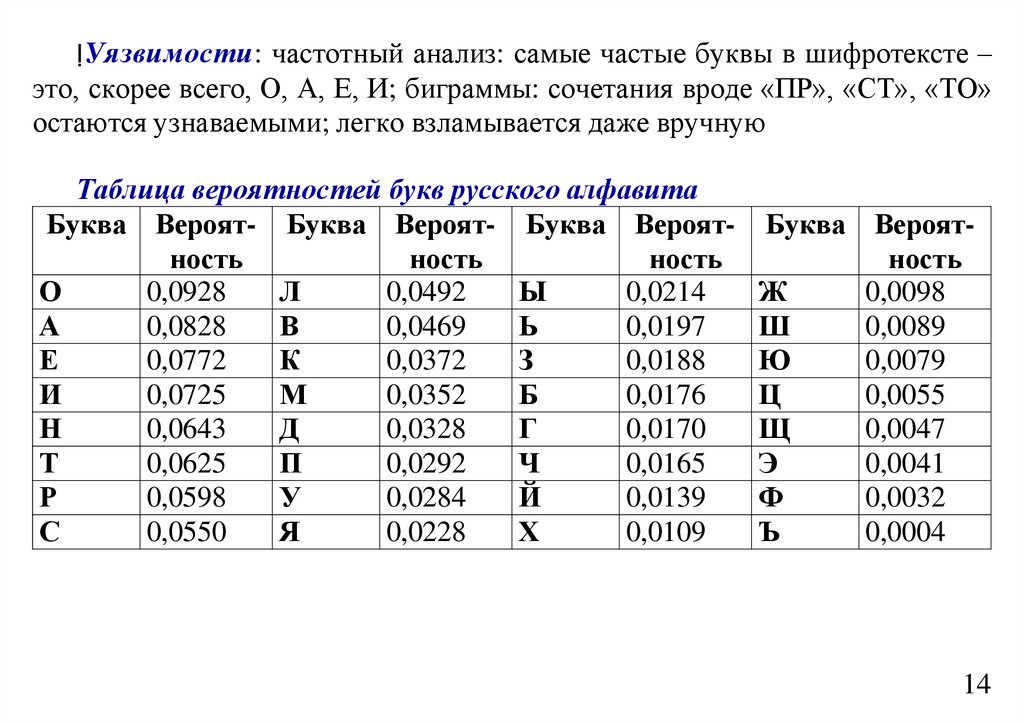


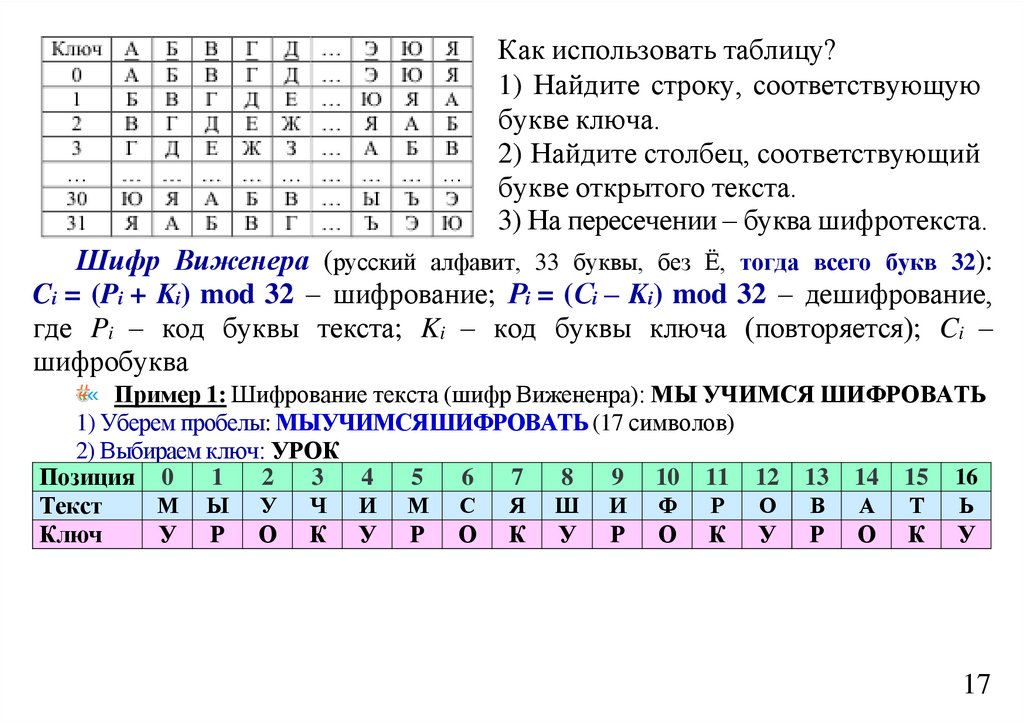
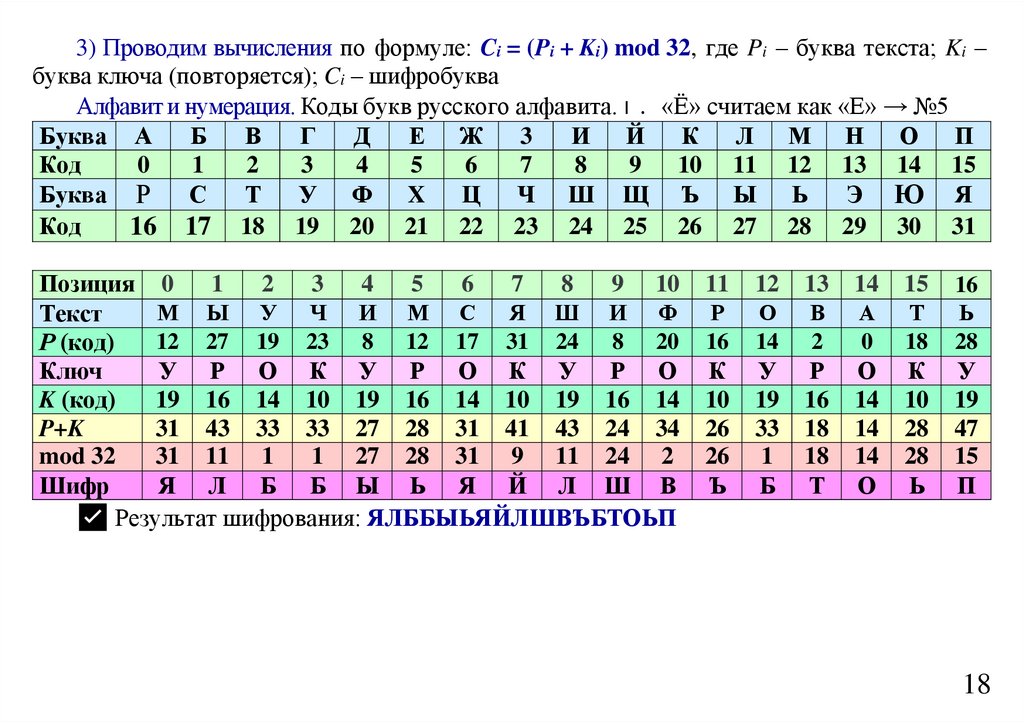
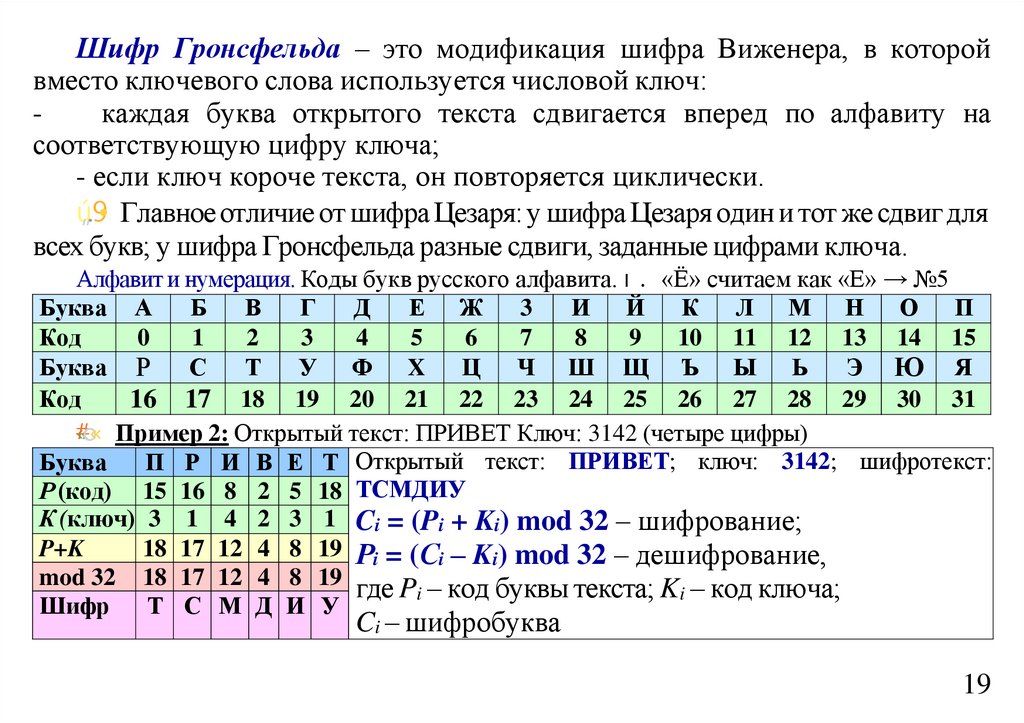
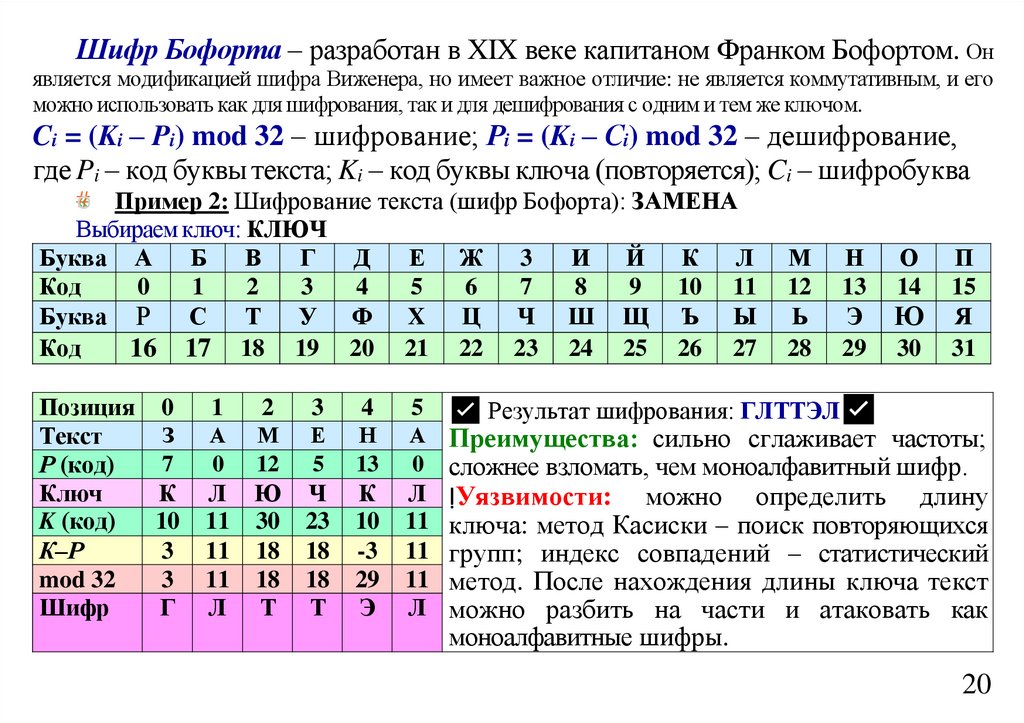






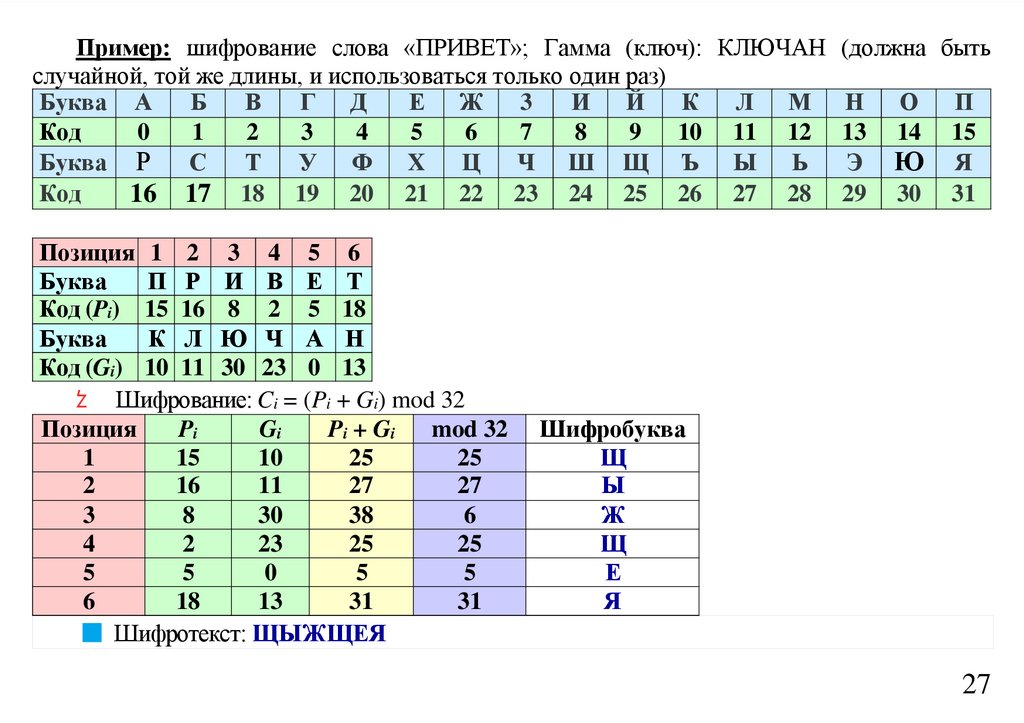







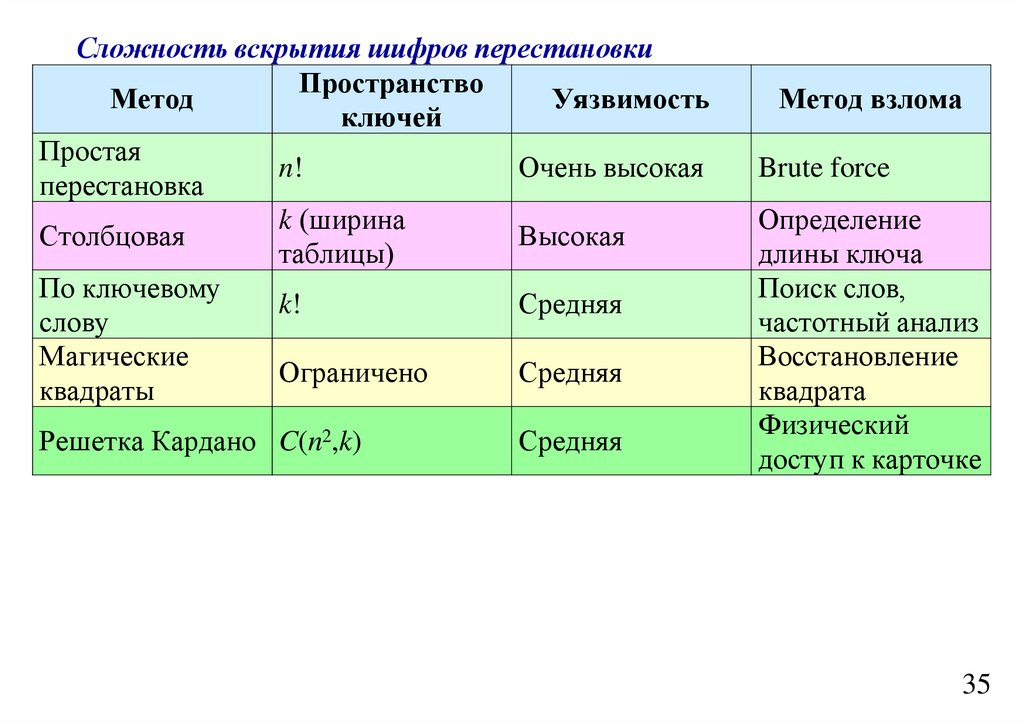














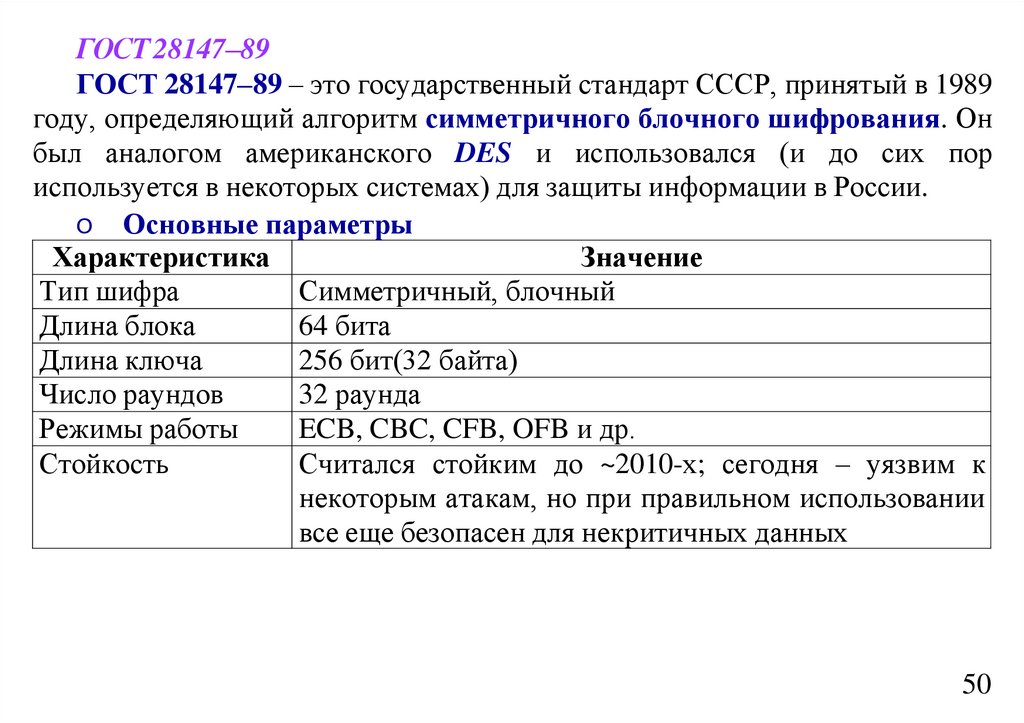








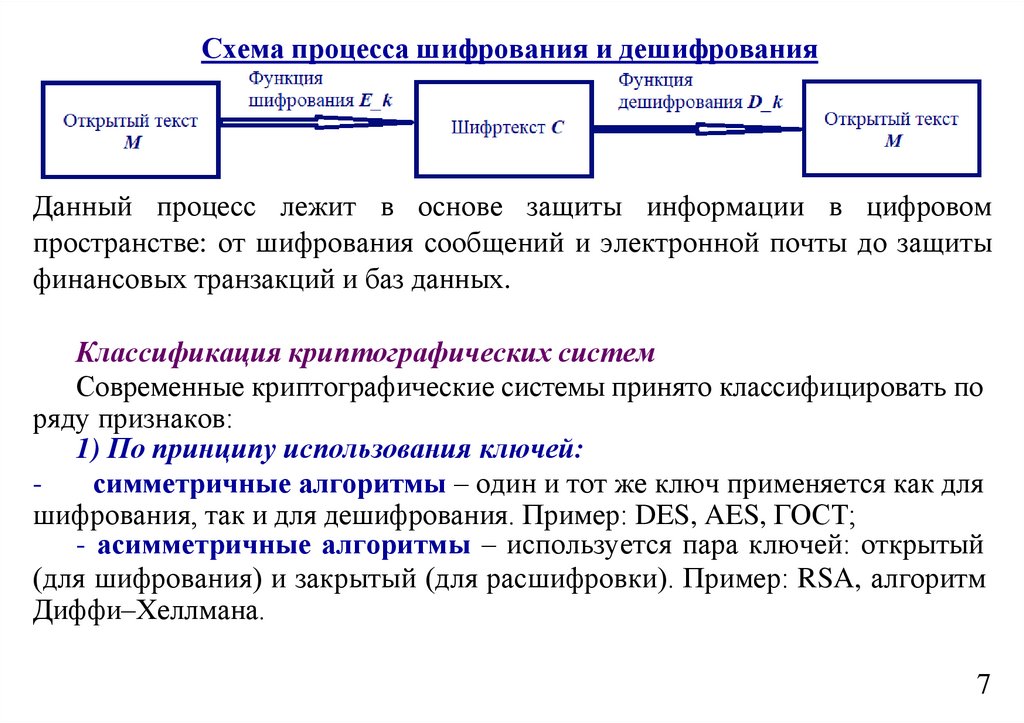





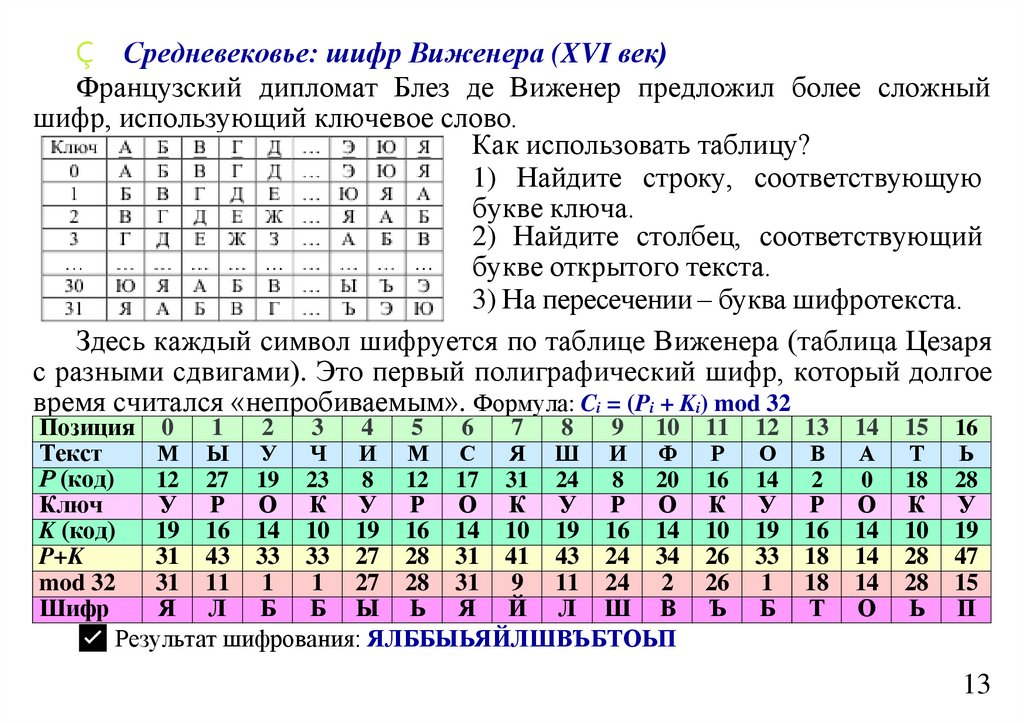

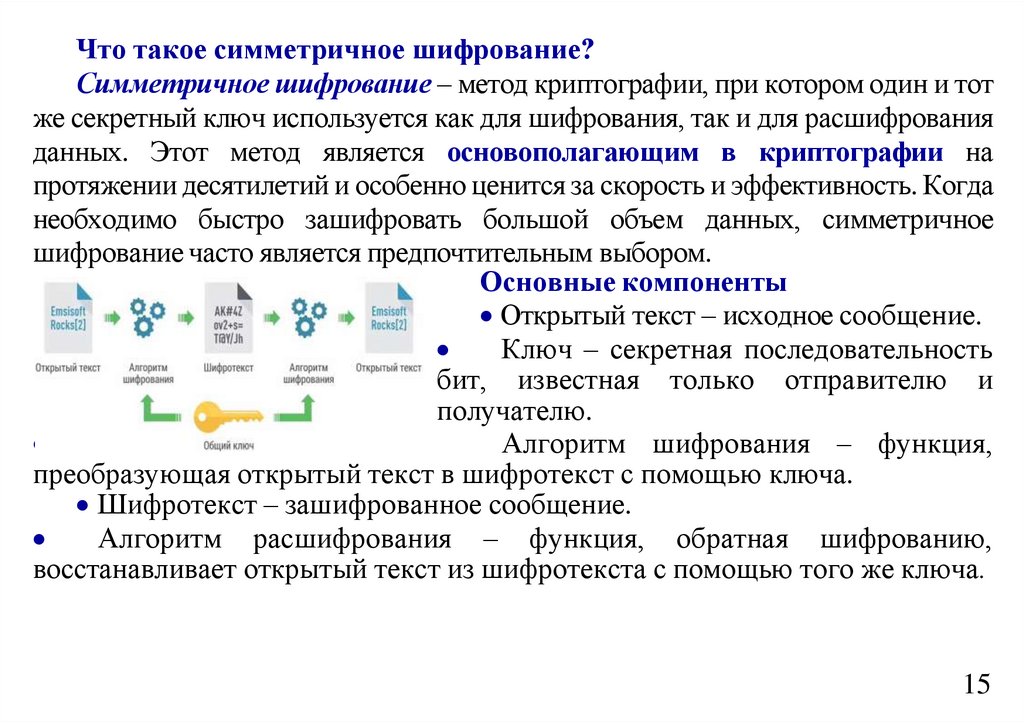

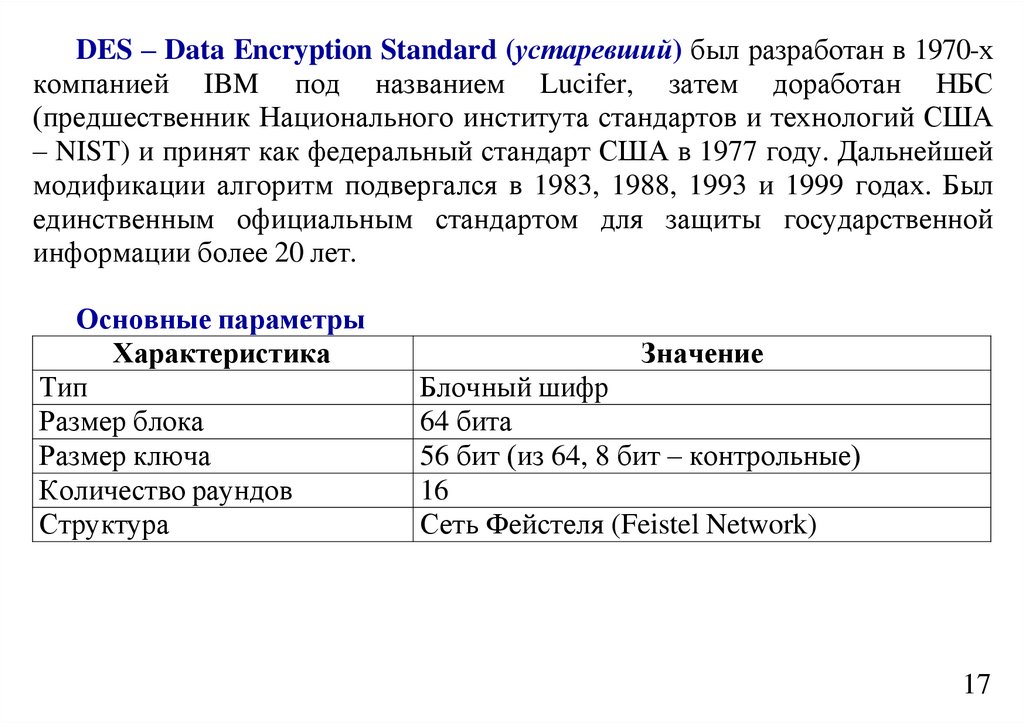


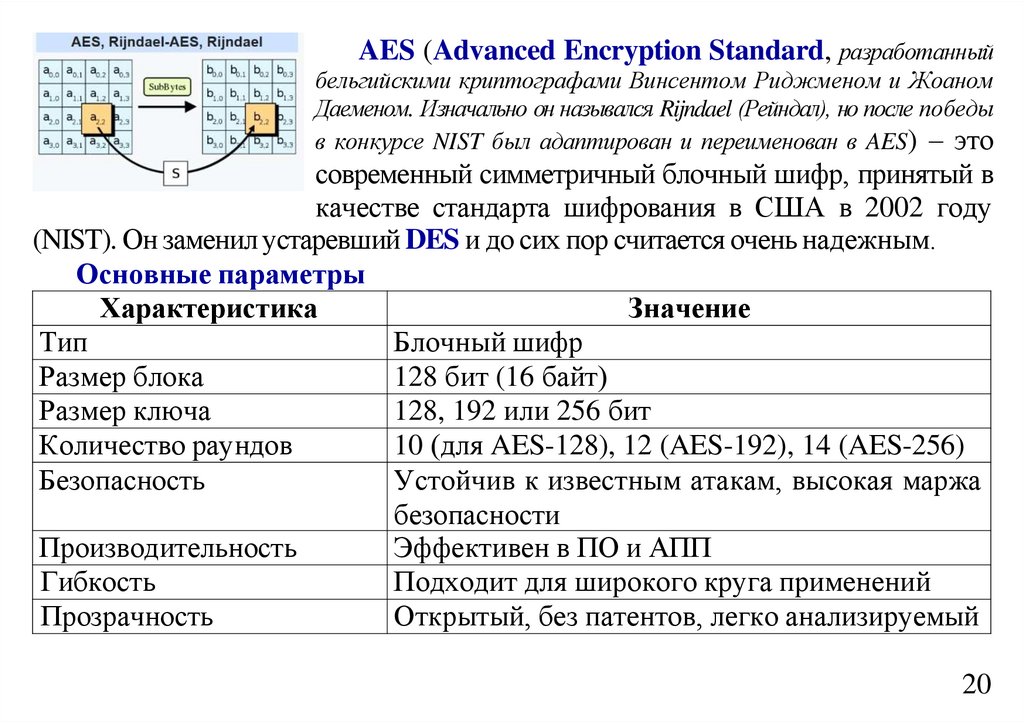








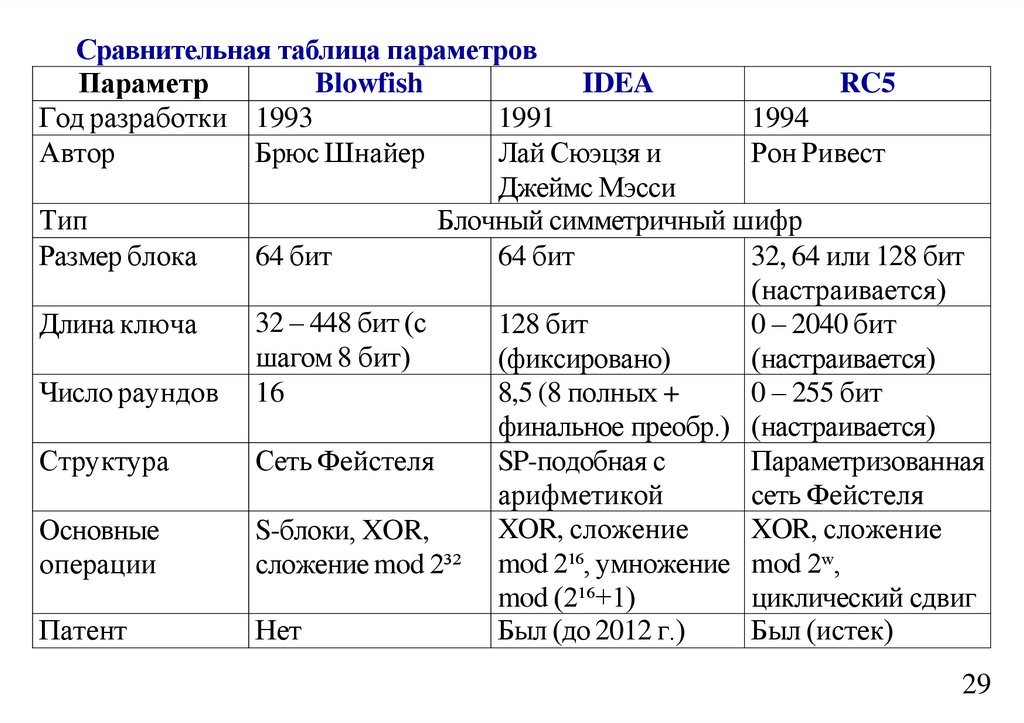








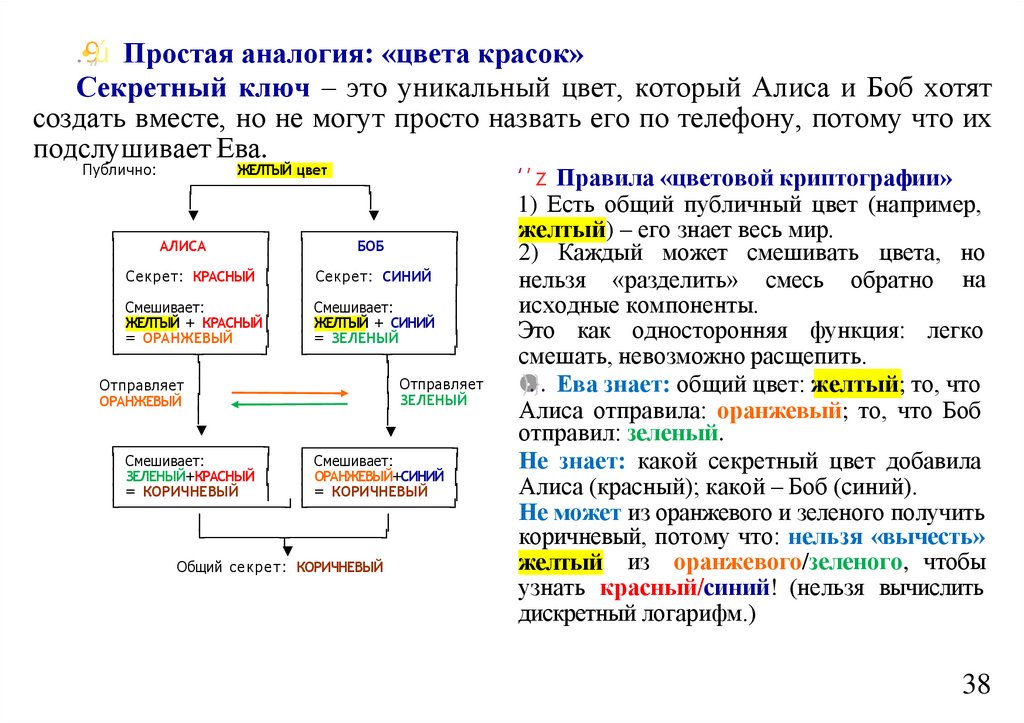





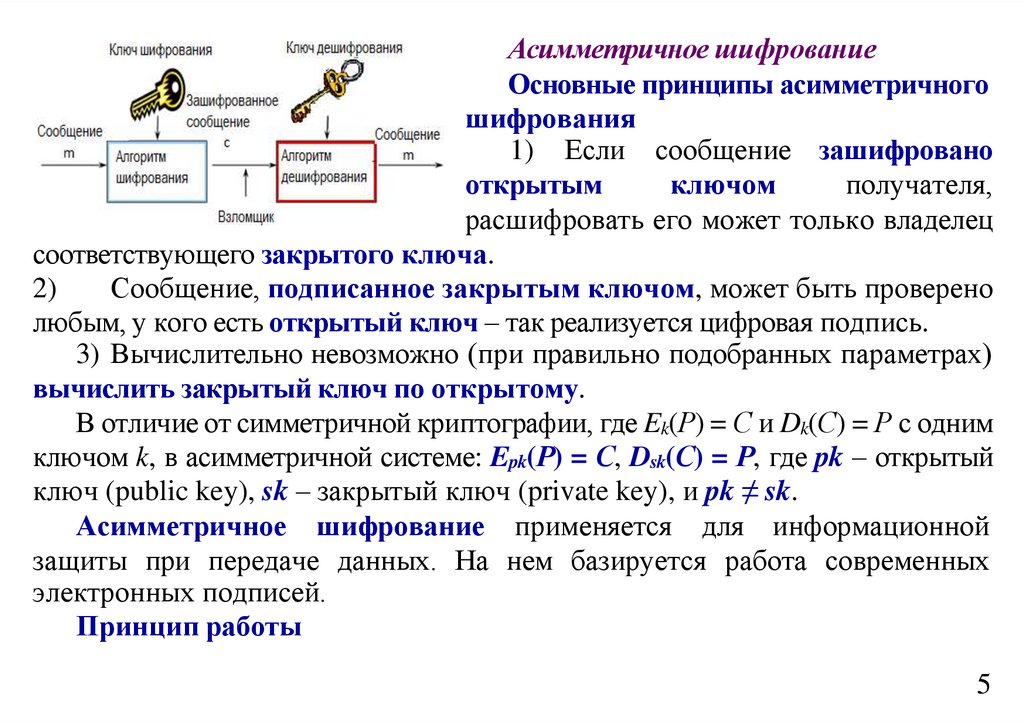
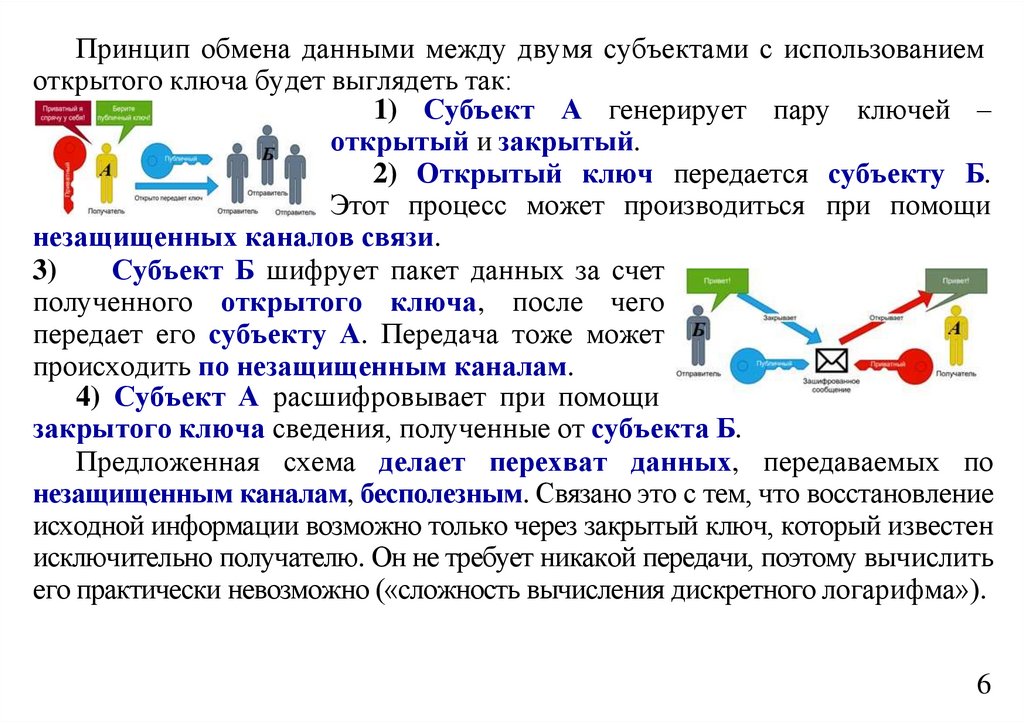
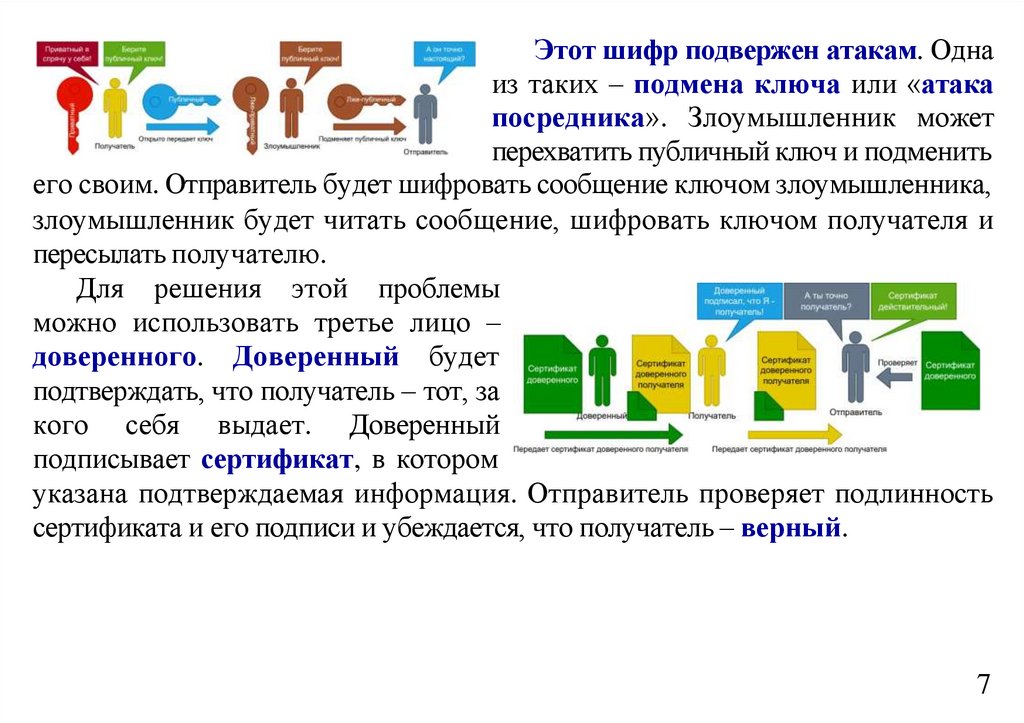
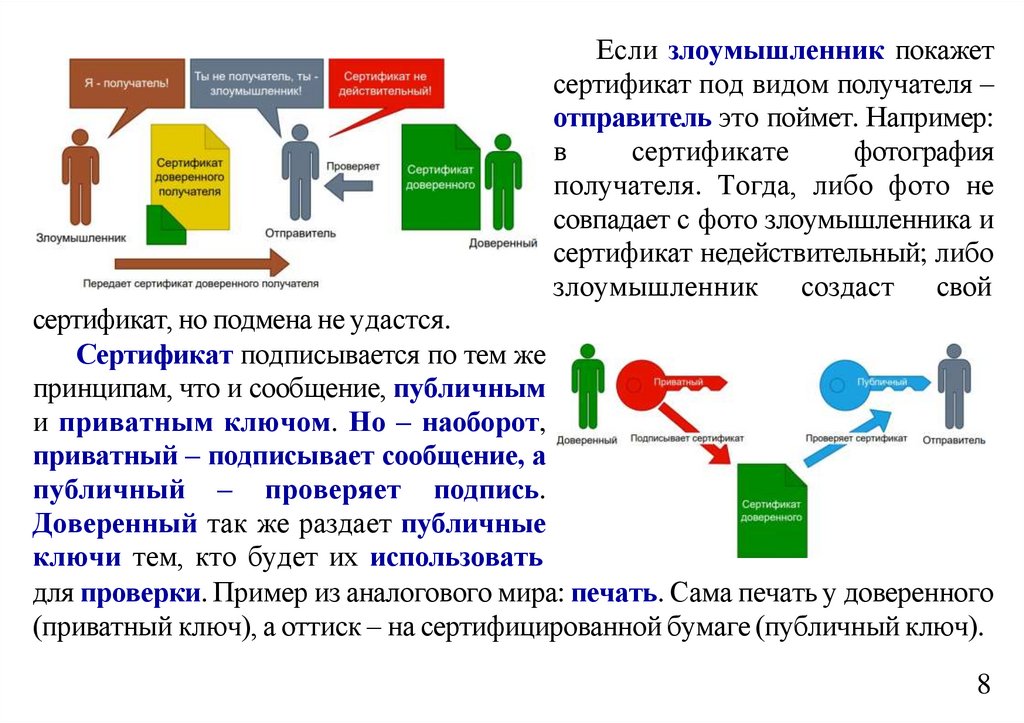

















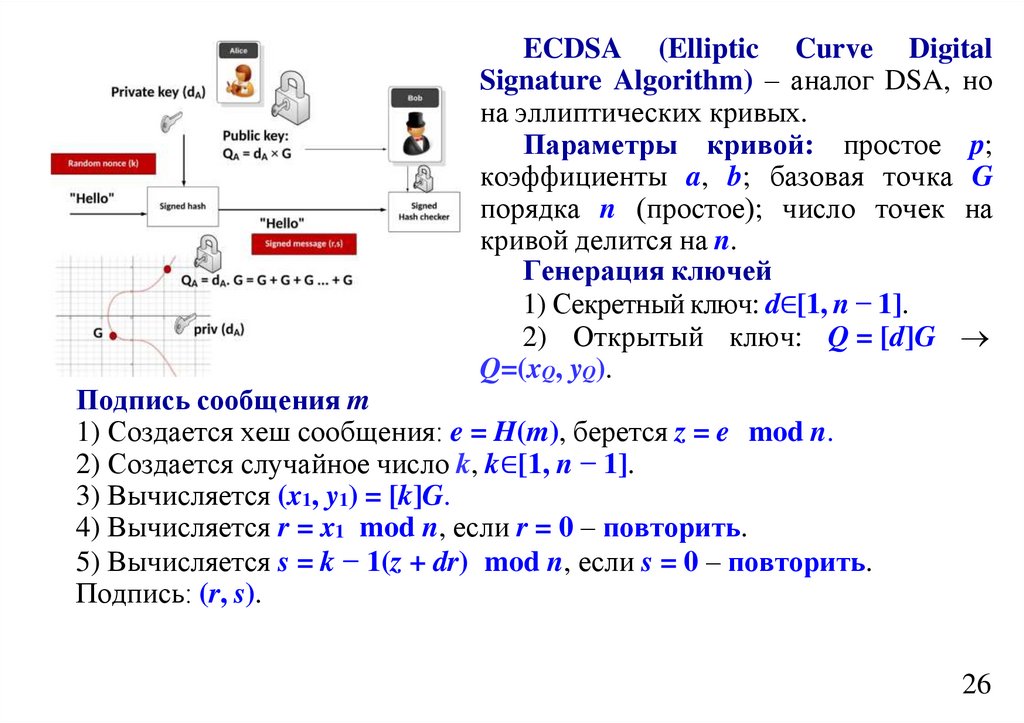









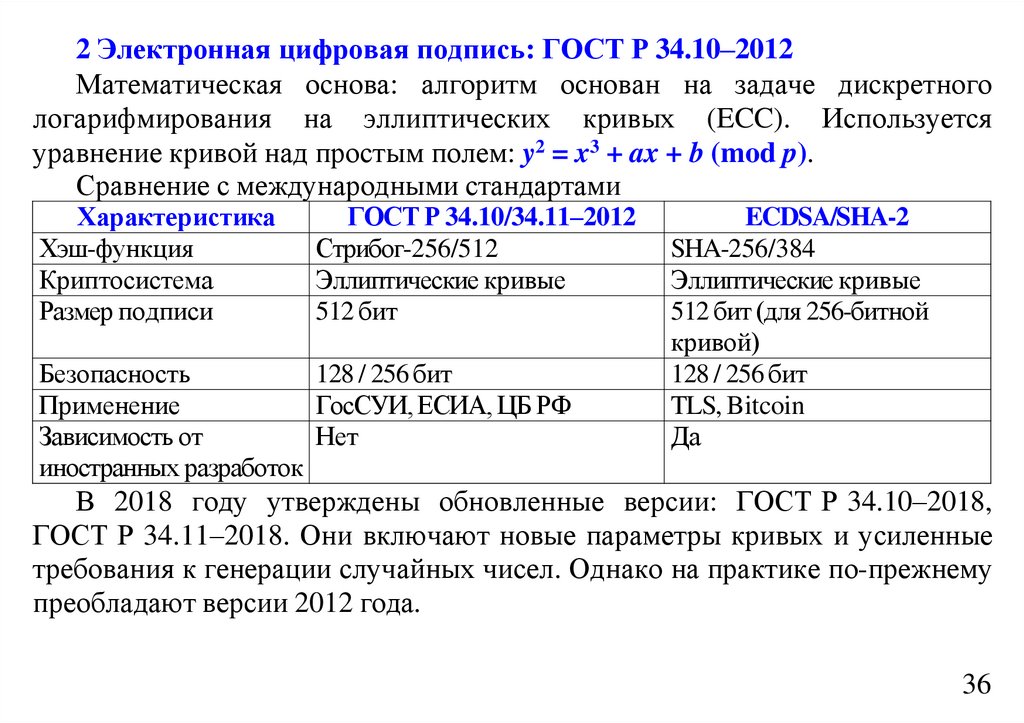
















































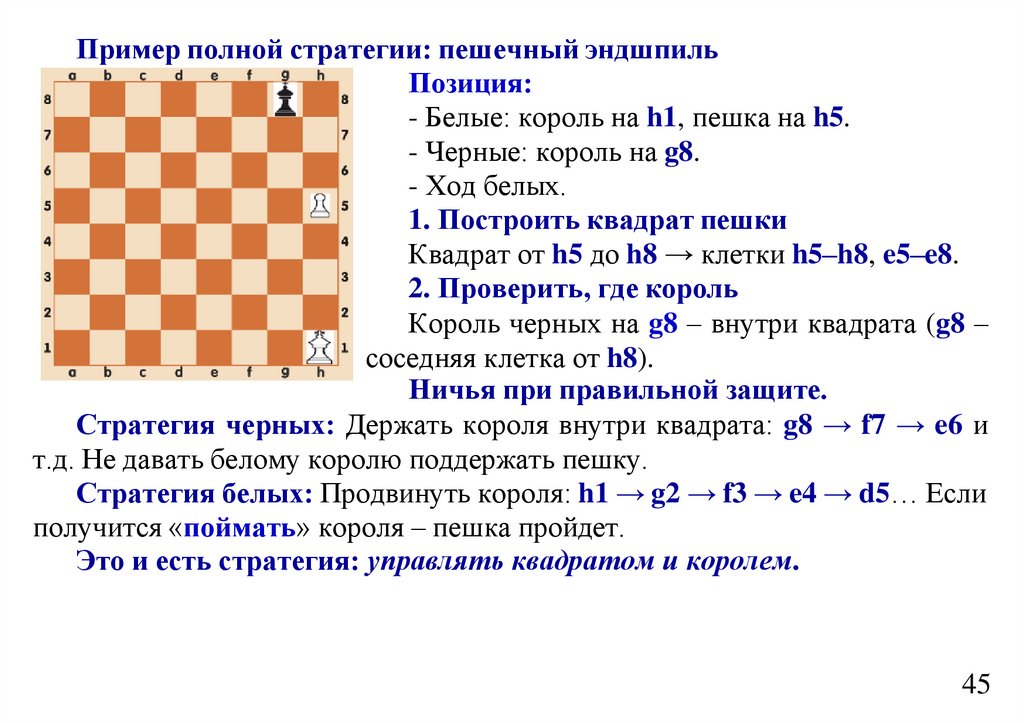















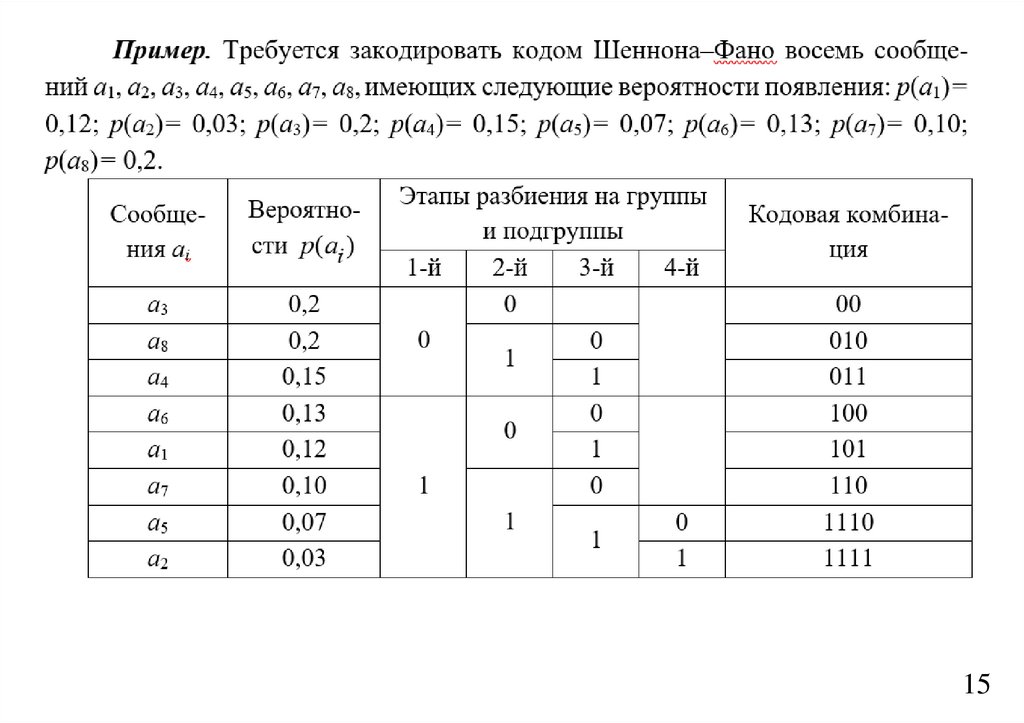































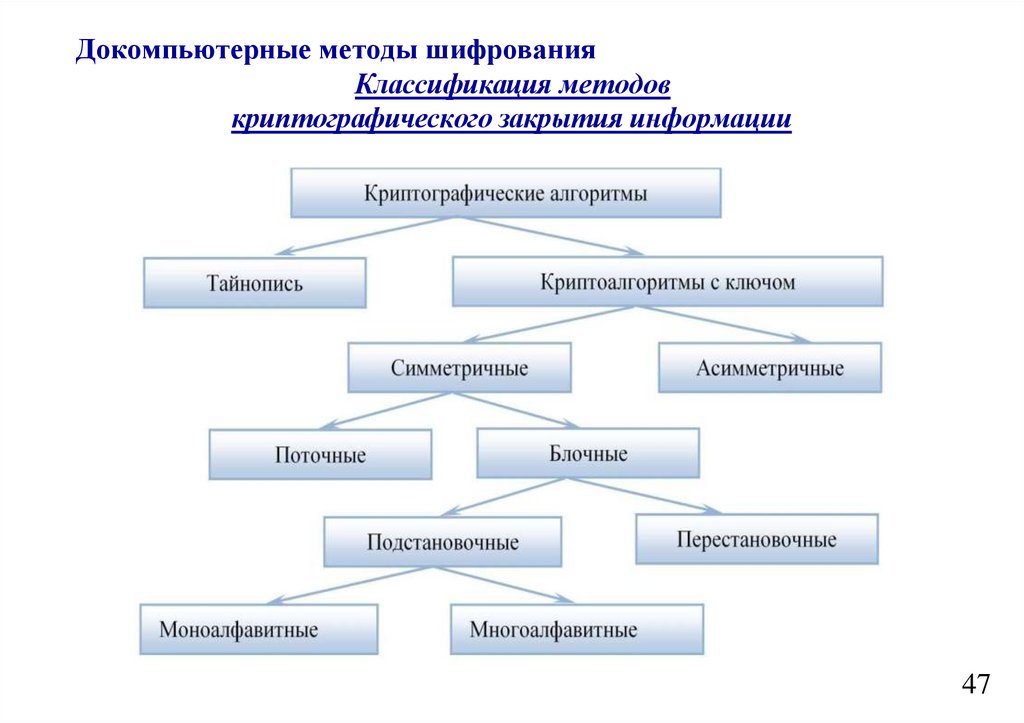
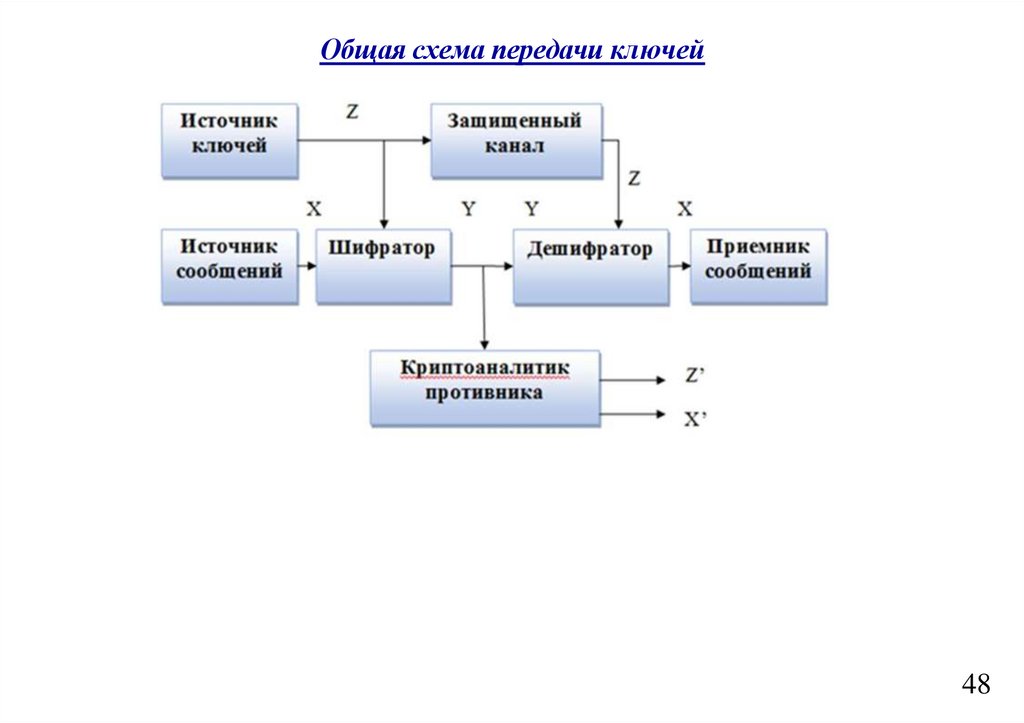
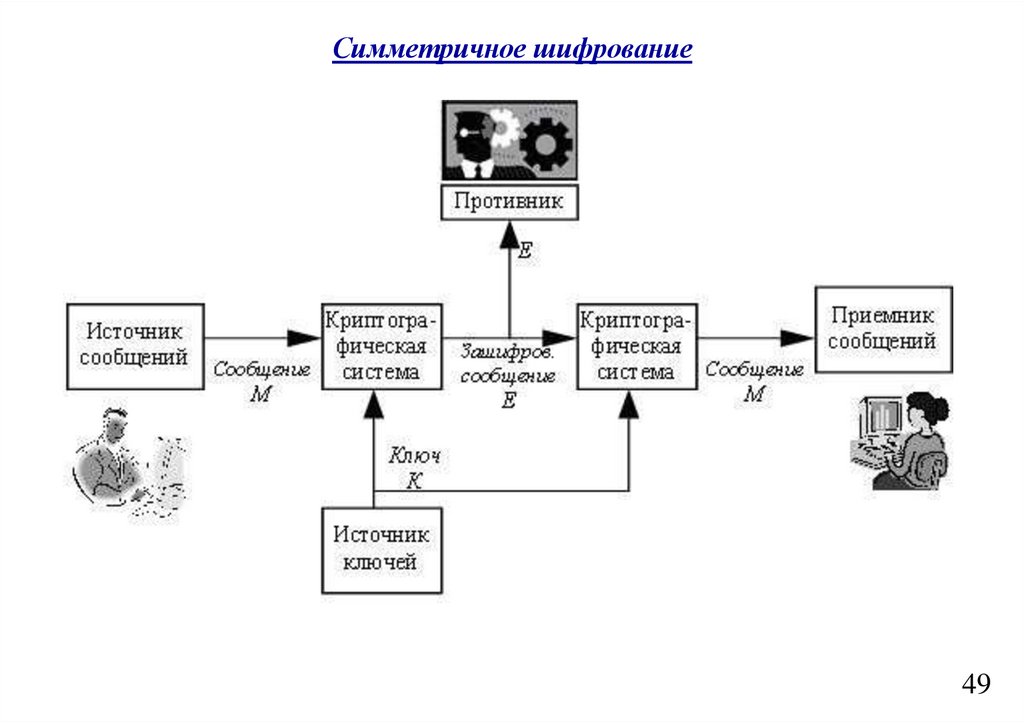

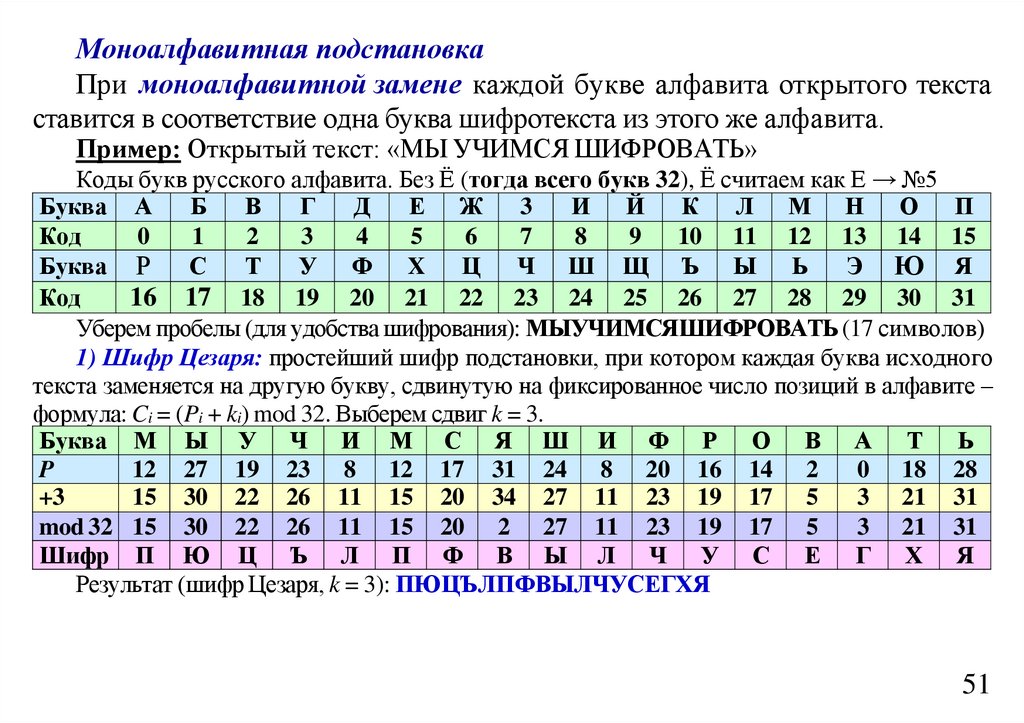
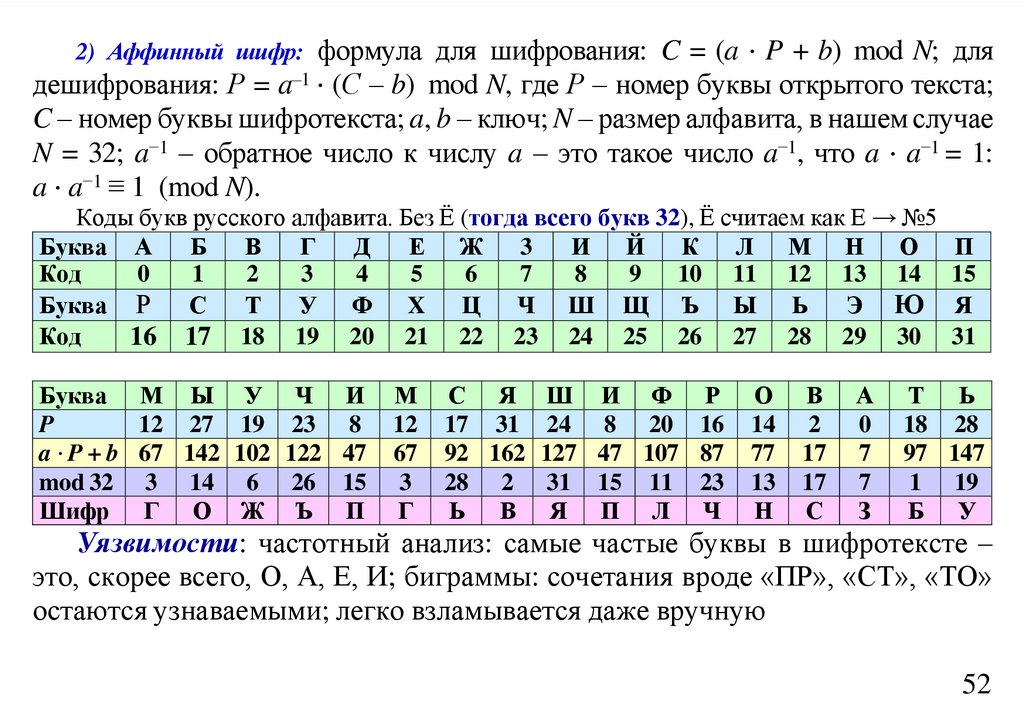
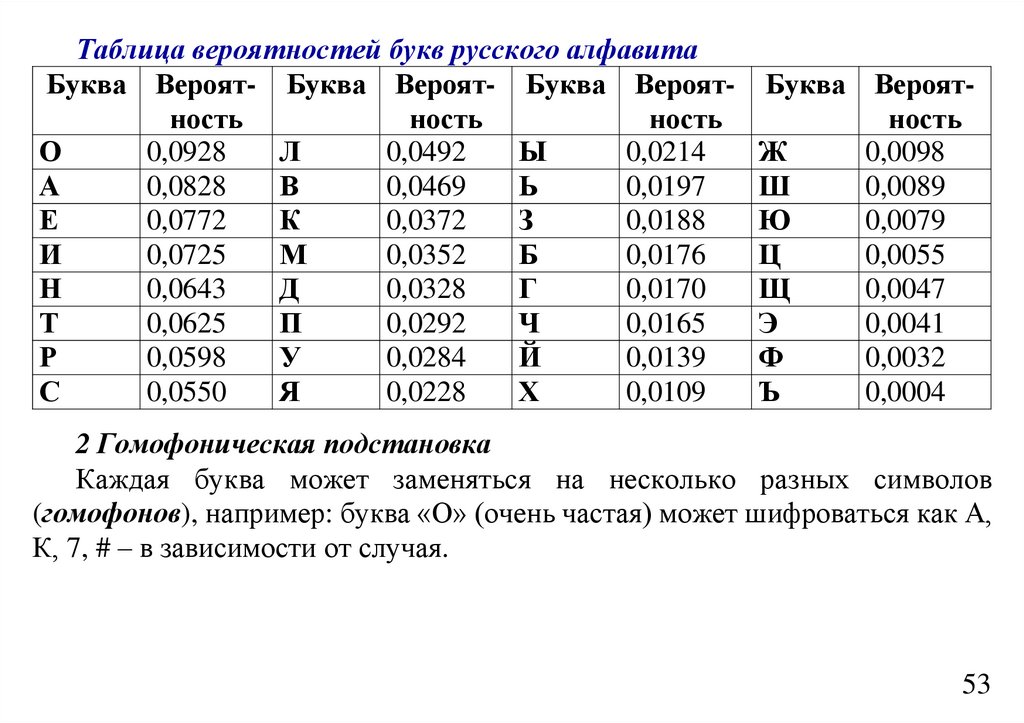

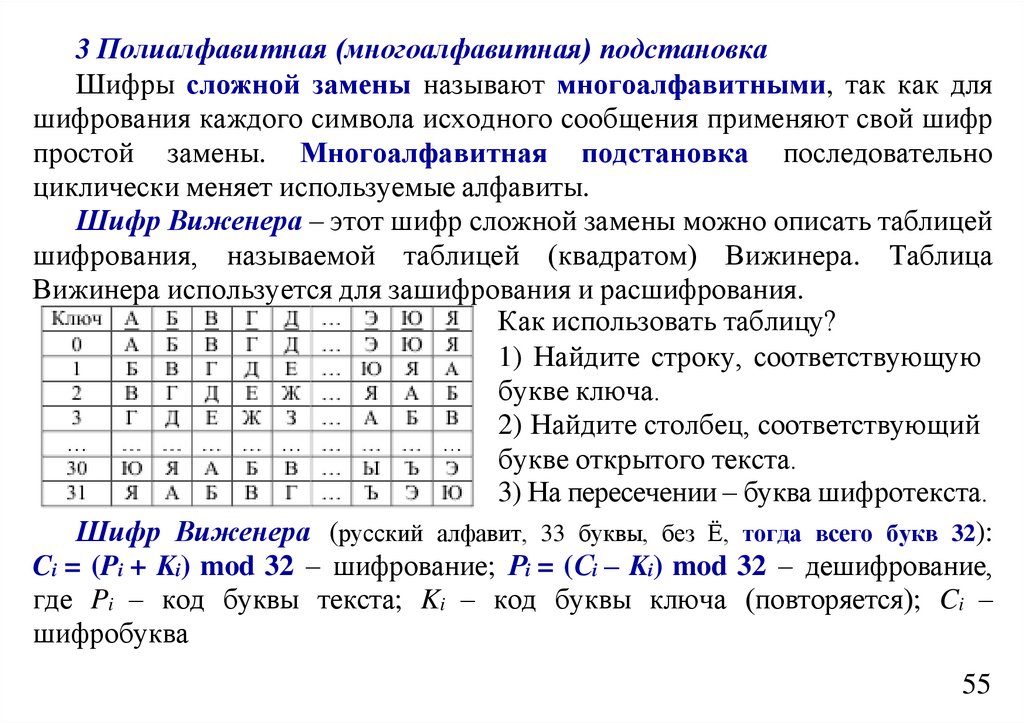
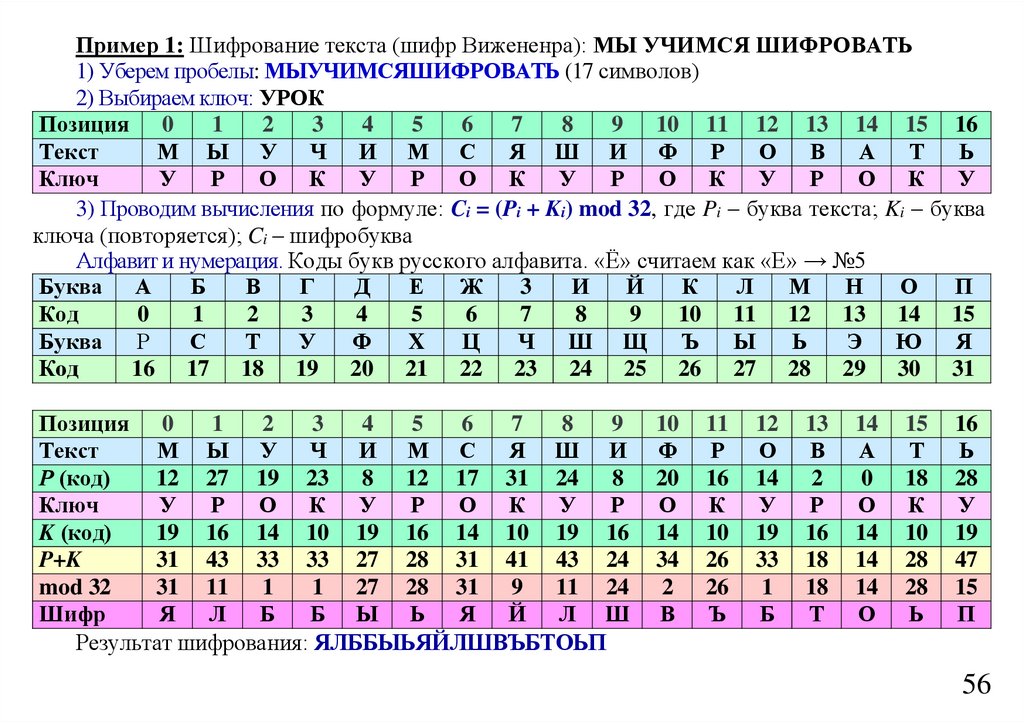
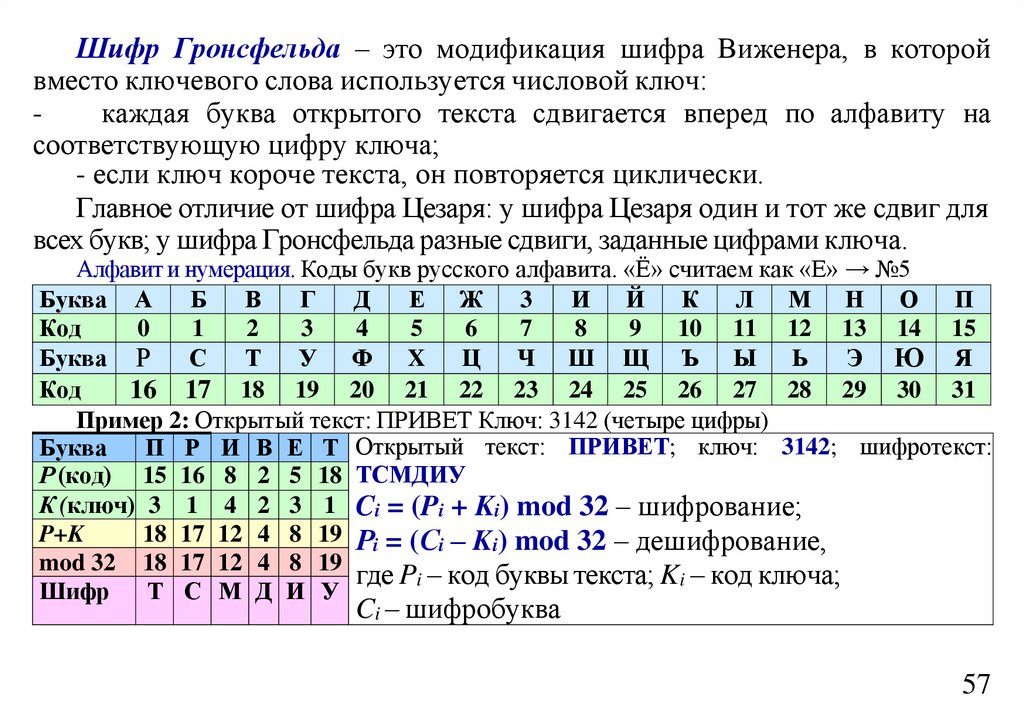
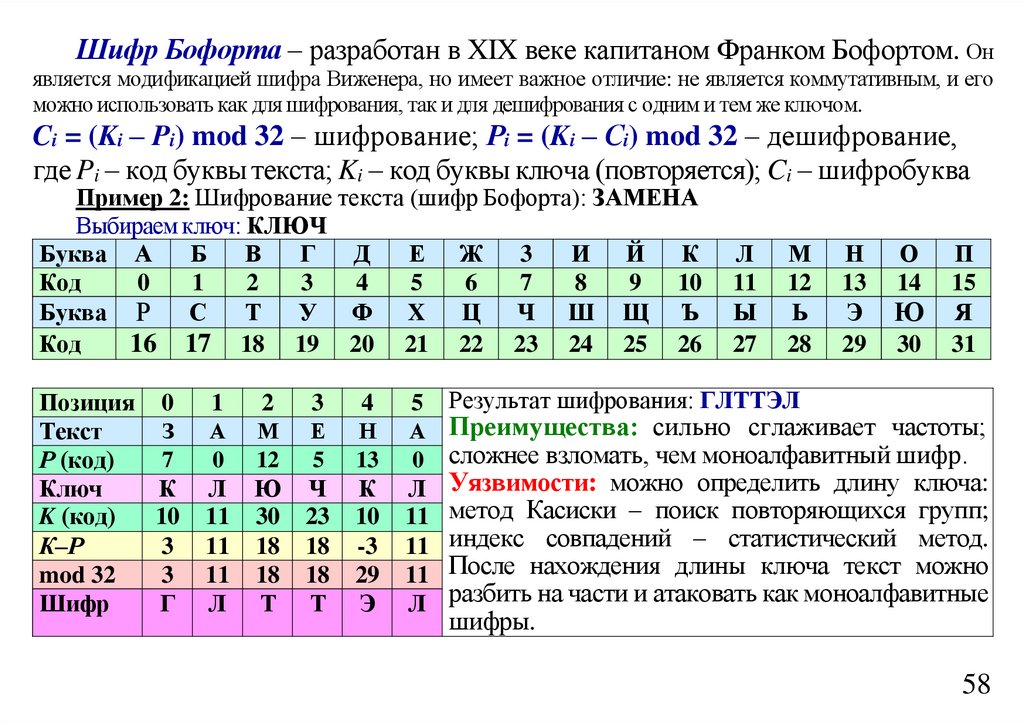




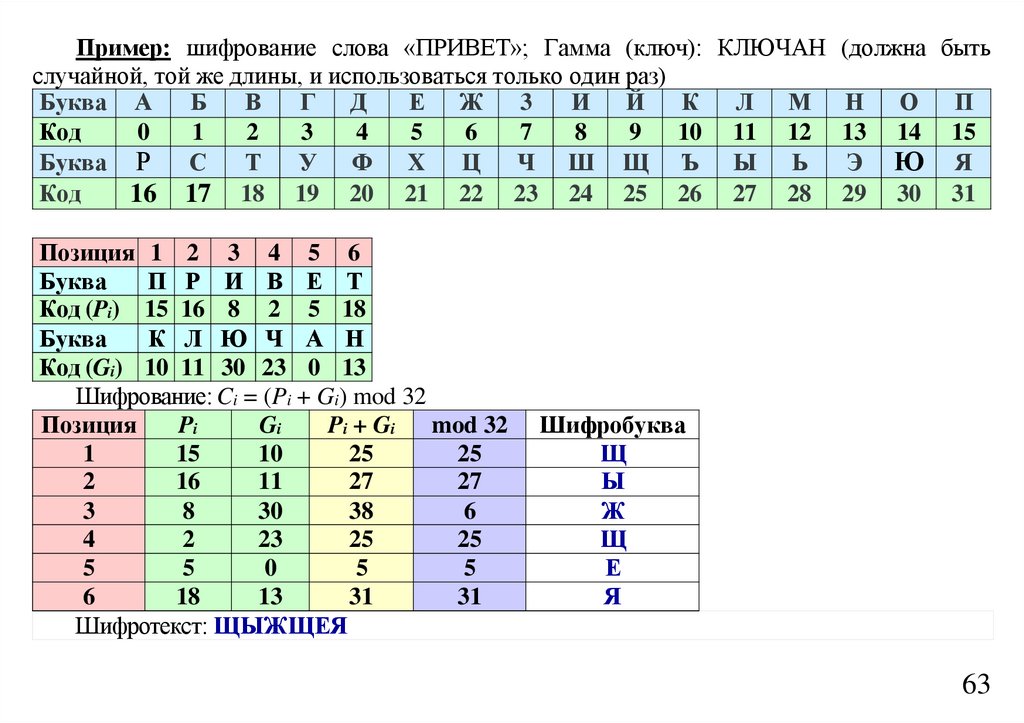

















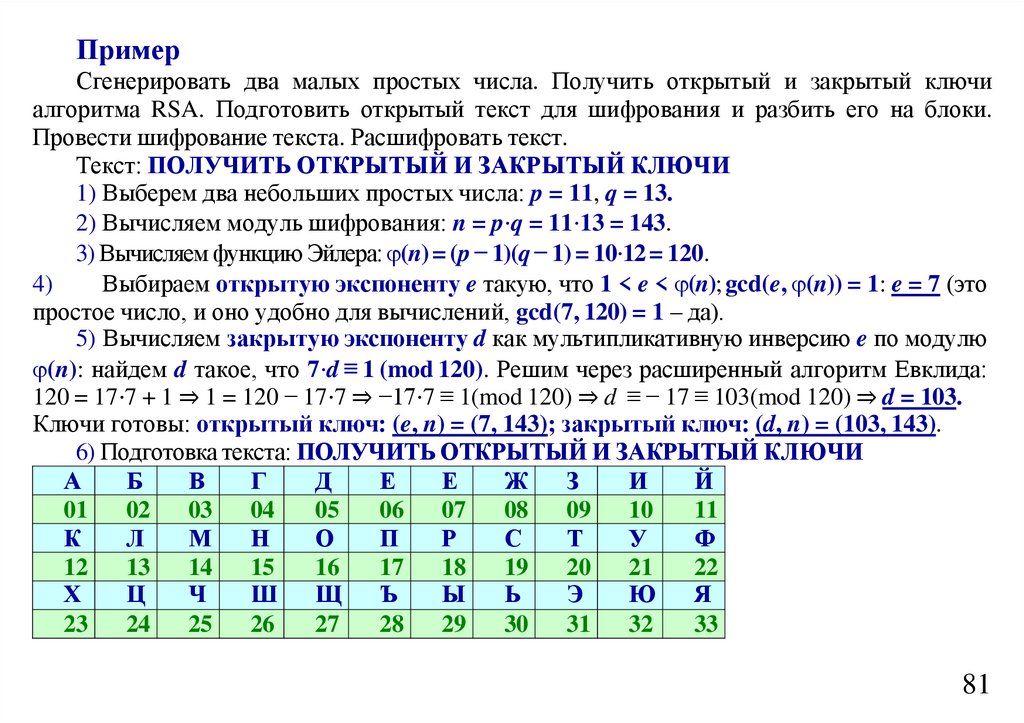
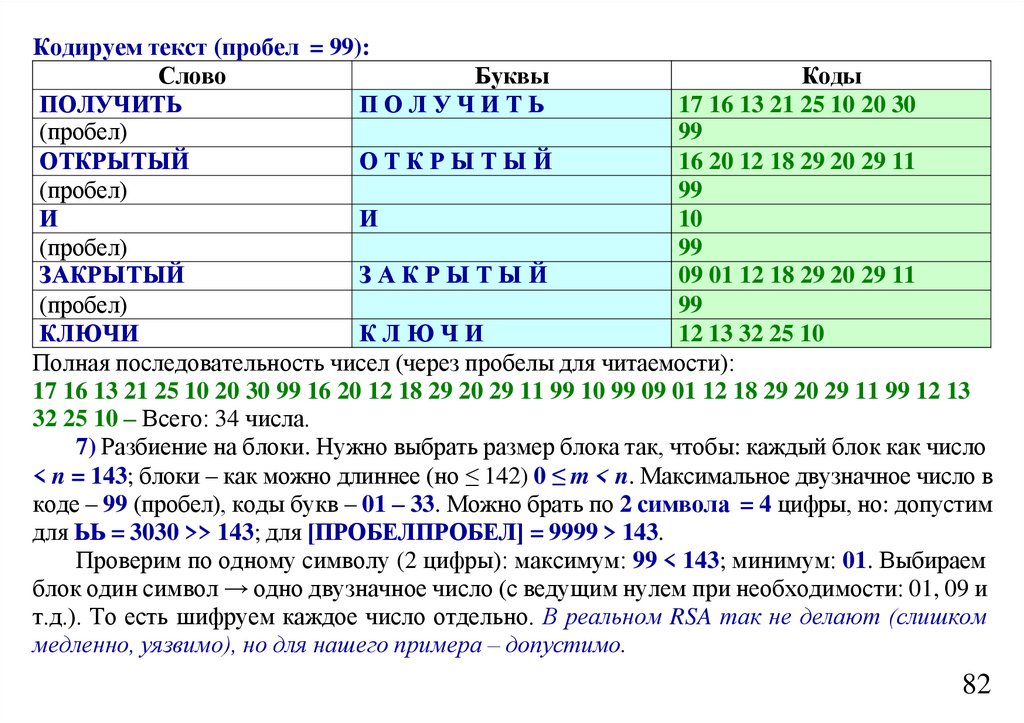

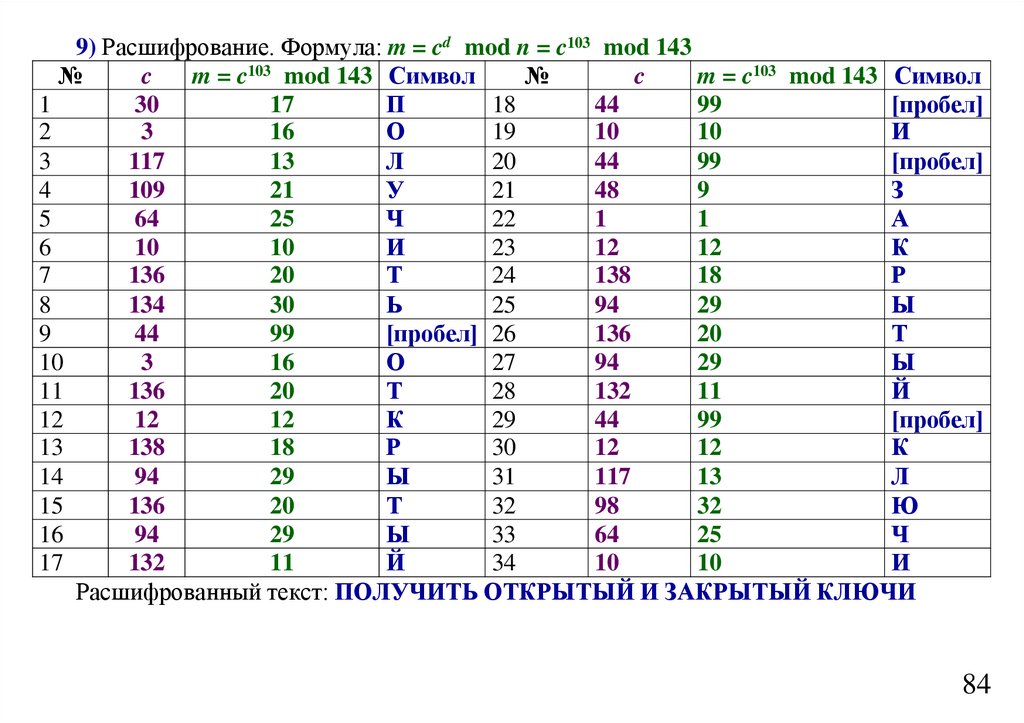















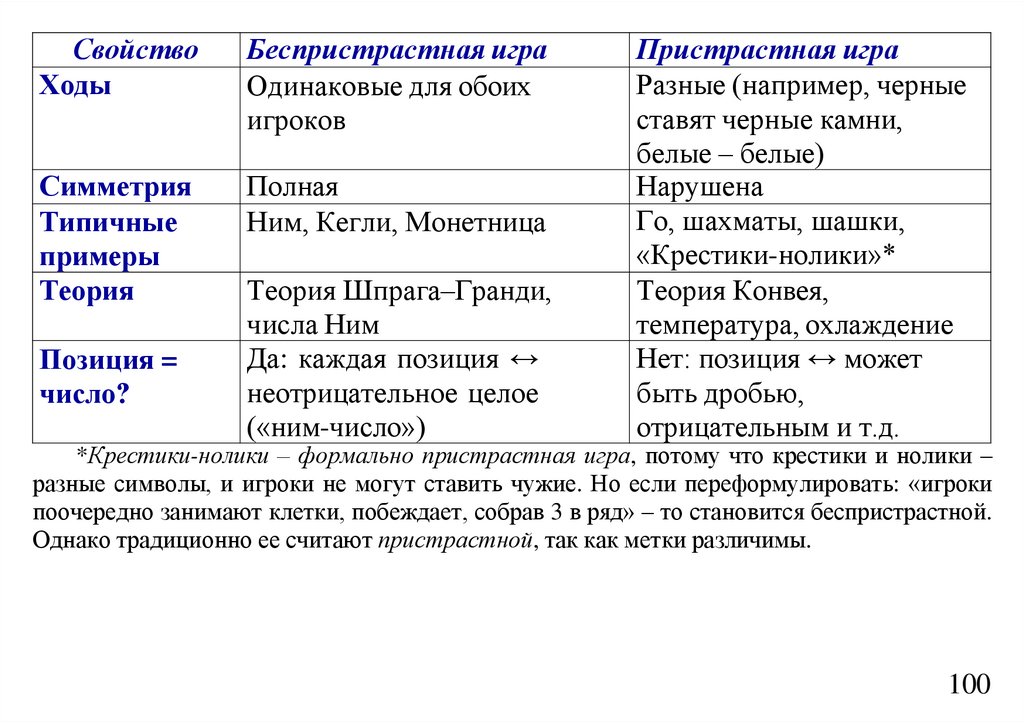















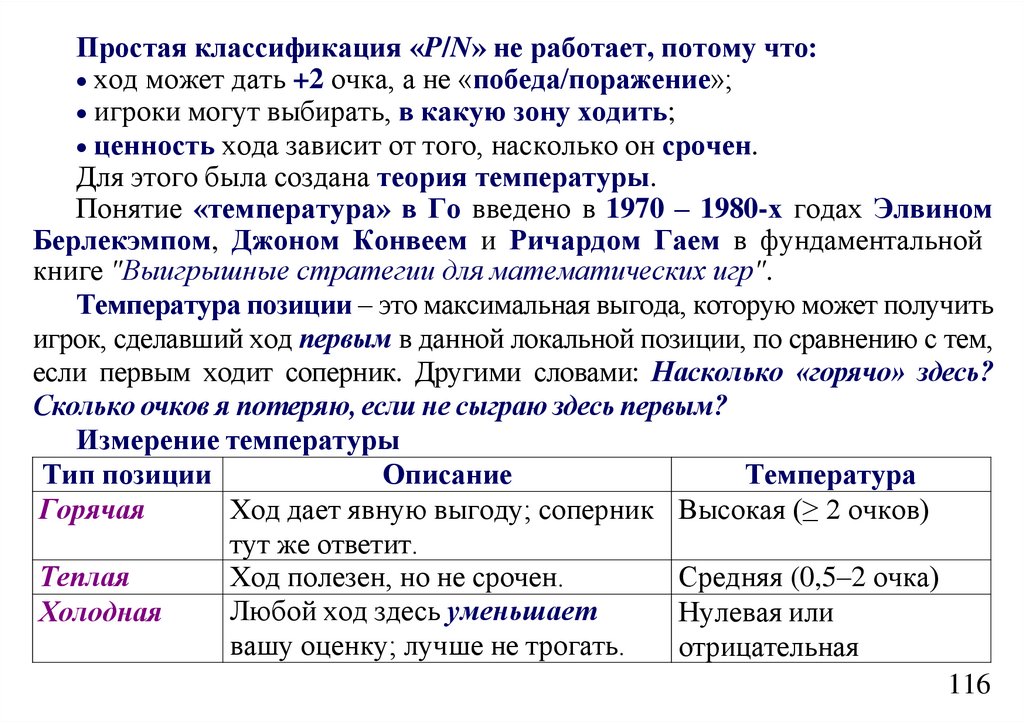





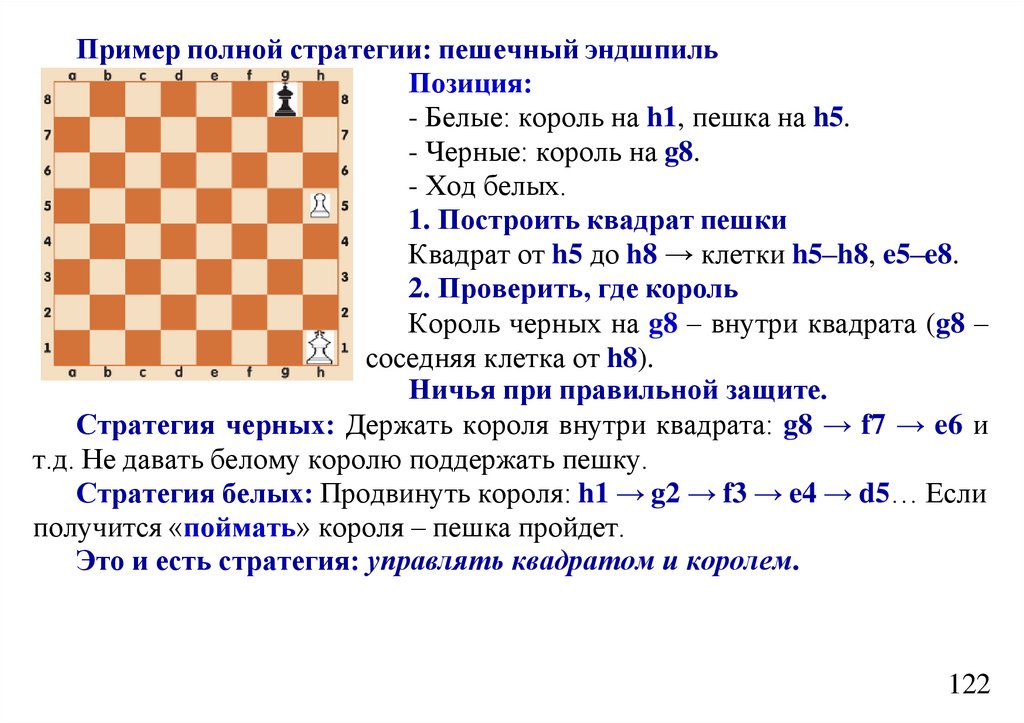

 informatics
informatics








