Лек Тема 02-3 Погр и МО

1.

Тема 2. Погрешности и математическая
обработка результатов измерений
Лекция 3
Классификация измерений
Учебные вопросы
1. Понятие об измерении.
2. Классификация измерений.

2.

2
2.1. Понятие об измерении
Измерение - это процесс экспериментального получения одного или более
значений величины, которые могут быть обоснованно приписаны величине .
Сущность измерения состоит в сравнении двух физических величин:
измеряемой, которая выражает интересующую особенность исследуемого
объекта, и известной, которая присуща специально созданному объекту ‒ мере.
Сравниваемые величины должны быть однородны, т.е. иметь одинаковую
физическую природу, и их размерности должны совпадать.
Для проведения измерения необходимо выполнение следующих условий:
подлежащая измерению физическая величина должна быть однозначно
определена;
единица измерения должна быть установлена соглашением или законом.

3.

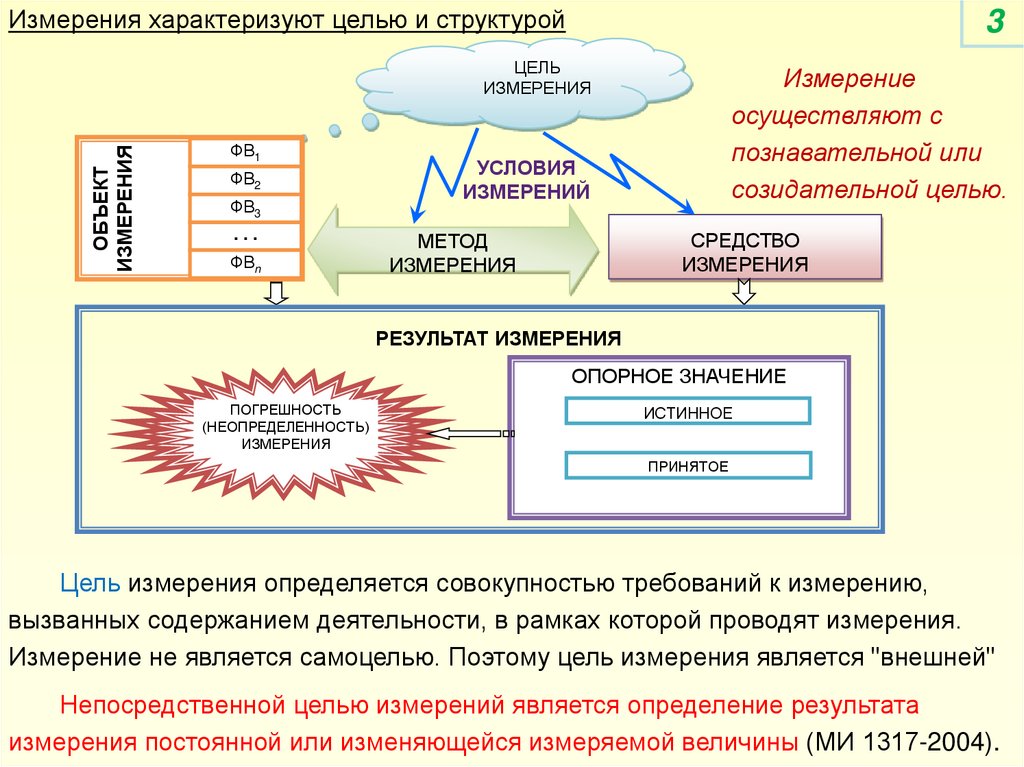
Измерения характеризуют целью и структурой
3
ОБЪЕКТ
ИЗМЕРЕНИЯ
ЦЕЛЬ
ИЗМЕРЕНИЯ
ФВ1
ФВ2
ФВ3
...
ФВn
Измерение
осуществляют с
познавательной или
созидательной целью.
УСЛОВИЯ
ИЗМЕРЕНИЙ
СРЕДСТВО
ИЗМЕРЕНИЯ
МЕТОД
ИЗМЕРЕНИЯ
РЕЗУЛЬТАТ ИЗМЕРЕНИЯ
ОПОРНОЕ ЗНАЧЕНИЕ
ПОГРЕШНОСТЬ
(НЕОПРЕДЕЛЕННОСТЬ)
ИЗМЕРЕНИЯ
ИСТИННОЕ
ПРИНЯТОЕ
Цель измерения определяется совокупностью требований к измерению,
вызванных содержанием деятельности, в рамках которой проводят измерения.
Измерение не является самоцелью. Поэтому цель измерения является "внешней"
Непосредственной целью измерений является определение результата
измерения постоянной или изменяющейся измеряемой величины (МИ 1317-2004).

4.

4
ОБЪЕКТ
ИЗМЕРЕНИЯ
ЦЕЛЬ
ИЗМЕРЕНИЯ
ФВ1
ФВ2
ФВ3
...
ФВn
УСЛОВИЯ
ИЗМЕРЕНИЙ
МЕТОД
ИЗМЕРЕНИЯ
СРЕДСТВО
ИЗМЕРЕНИЯ
РЕЗУЛЬТАТ ИЗМЕРЕНИЯ
ОПОРНОЕ ЗНАЧЕНИЕ
ПОГРЕШНОСТЬ
(НЕОПРЕДЕЛЕННОСТЬ)
ИЗМЕРЕНИЯ
ИСТИННОЕ
ПРИНЯТОЕ
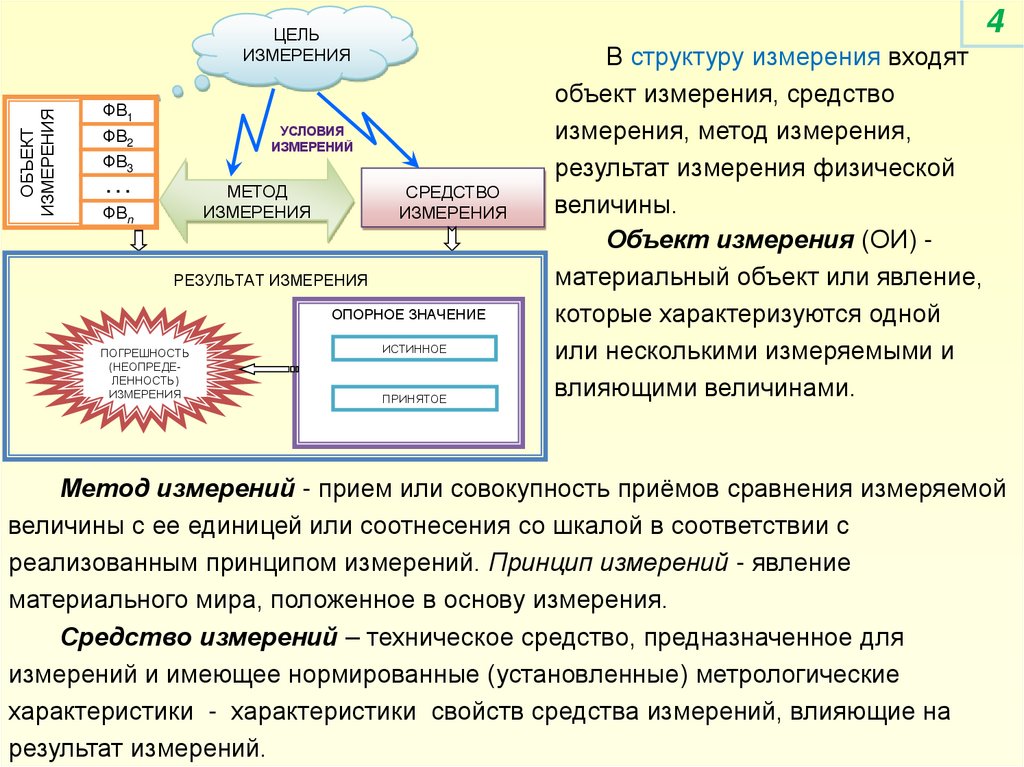
В структуру измерения входят
объект измерения, средство
измерения, метод измерения,
результат измерения физической
величины.
Объект измерения (ОИ) материальный объект или явление,
которые характеризуются одной
или несколькими измеряемыми и
влияющими величинами.
Метод измерений - прием или совокупность приёмов сравнения измеряемой
величины с ее единицей или соотнесения со шкалой в соответствии с
реализованным принципом измерений. Принцип измерений - явление
материального мира, положенное в основу измерения.
Средство измерений – техническое средство, предназначенное для
измерений и имеющее нормированные (установленные) метрологические
характеристики - характеристики свойств средства измерений, влияющие на
результат измерений.

5.

5
ОБЪЕКТ
ИЗМЕРЕНИЯ
ЦЕЛЬ
ИЗМЕРЕНИЯ
ФВ1
ФВ2
ФВ3
...
ФВn
УСЛОВИЯ
ИЗМЕРЕНИЙ
МЕТОД
ИЗМЕРЕНИЯ
СРЕДСТВО
ИЗМЕРЕНИЯ
РЕЗУЛЬТАТ ИЗМЕРЕНИЯ
ОПОРНОЕ ЗНАЧЕНИЕ
ПОГРЕШНОСТЬ
(НЕОПРЕДЕЛЕННОСТЬ)
ИЗМЕРЕНИЯ
ИСТИННОЕ
ПРИНЯТОЕ
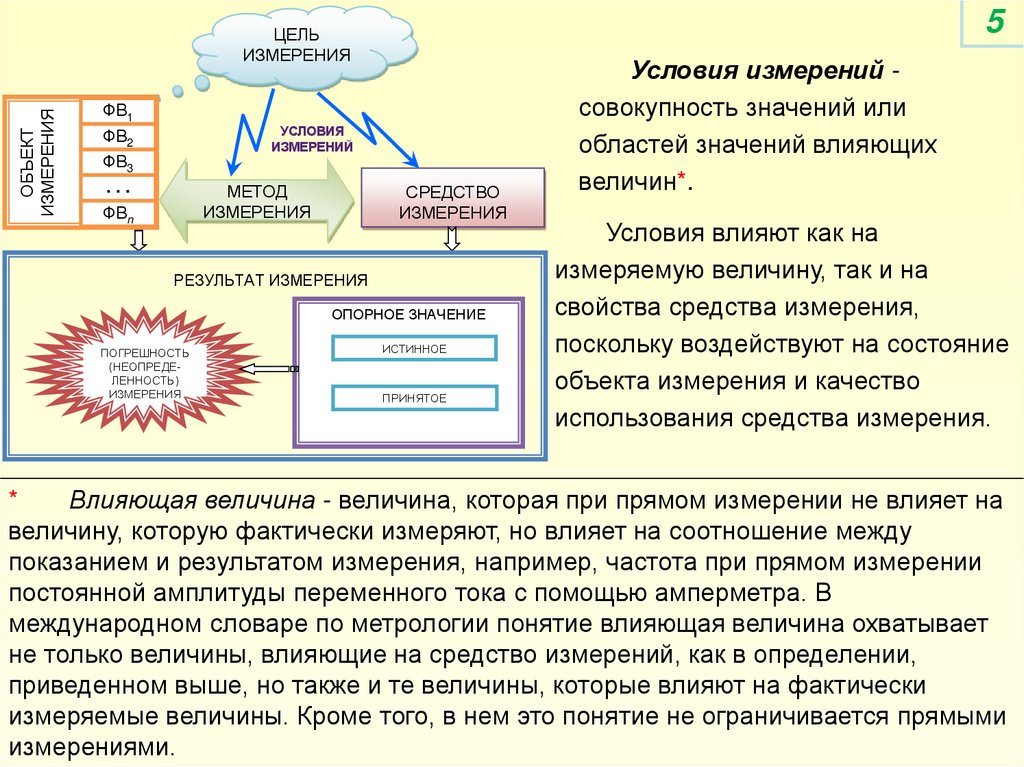
Условия измерений совокупность значений или
областей значений влияющих
величин*.
Условия влияют как на
измеряемую величину, так и на
свойства средства измерения,
поскольку воздействуют на состояние
объекта измерения и качество
использования средства измерения.
*
Влияющая величина - величина, которая при прямом измерении не влияет на
величину, которую фактически измеряют, но влияет на соотношение между
показанием и результатом измерения, например, частота при прямом измерении
постоянной амплитуды переменного тока с помощью амперметра. В
международном словаре по метрологии понятие влияющая величина охватывает
не только величины, влияющие на средство измерений, как в определении,
приведенном выше, но также и те величины, которые влияют на фактически
измеряемые величины. Кроме того, в нем это понятие не ограничивается прямыми
измерениями.

6.

ОБЪЕКТ
ИЗМЕРЕНИЯ
ЦЕЛЬ
ИЗМЕРЕНИЯ
ФВ1
ФВ2
ФВ3
...
ФВn
УСЛОВИЯ
ИЗМЕРЕНИЙ
МЕТОД
ИЗМЕРЕНИЯ
СРЕДСТВО
ИЗМЕРЕНИЯ
РЕЗУЛЬТАТ ИЗМЕРЕНИЯ
ОПОРНОЕ ЗНАЧЕНИЕ
ПОГРЕШНОСТЬ
(НЕОПРЕДЕЛЕННОСТЬ)
ИЗМЕРЕНИЯ
ИСТИННОЕ
ПРИНЯТОЕ
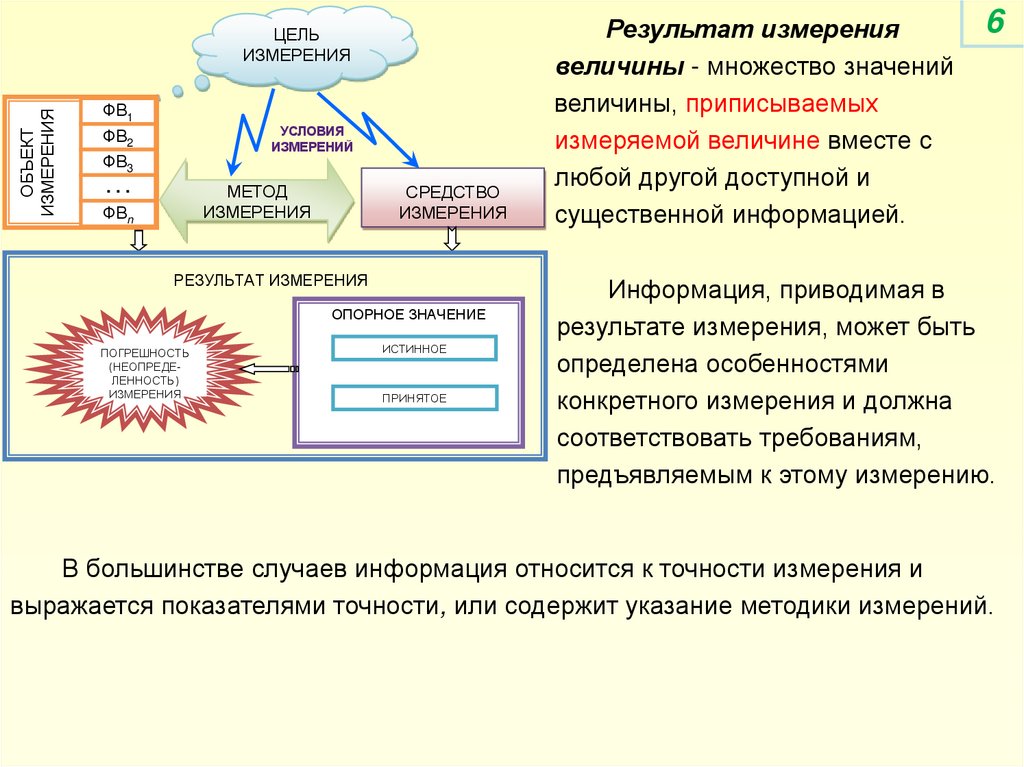
Результат измерения
величины - множество значений
величины, приписываемых
измеряемой величине вместе с
любой другой доступной и
существенной информацией.
6
Информация, приводимая в
результате измерения, может быть
определена особенностями
конкретного измерения и должна
соответствовать требованиям,
предъявляемым к этому измерению.
В большинстве случаев информация относится к точности измерения и
выражается показателями точности, или содержит указание методики измерений.

7.

Истинное значение величины – такое значение величины, которое
соответствует определению измеряемой величины.
7
Истинное значение неизвестно, его невозможно определить в процессе
измерения. Истинное значение соответствует некоему параметру модели объекта
измерения, но поскольку всегда есть несоответствие между объектом измерения и
его моделью, то всегда присутствует разность между результатом измерения и
истинным значением.
Измеренное значение величины - значение величины, которое
представляет результат измерения.

8.

При сопоставлении результата измерения с однородными величинами в
качестве основы для сопоставления используют понятие опорное значение
величины*.
8
Опорное значение величины может быть истинным значением величины,
подлежащей измерению, в этом случае оно неизвестно, или принятым значением
величины, в этом случае оно известно.
Принятое значение величины - значение величины, по соглашению
приписанное величине для данной цели.
Принятое значение величины может быть выбрано произвольно, может быть
оценкой истинного значения, однако во многих случаях в качестве принятого
используют действительное значение.
Действительное значение - значение величины, полученное
экспериментальным путем и настолько близкое к истинному значению, что в
поставленной измерительной задаче может быть использовано вместо него.
*
Опорное значение величины - значение величины, которое используют в
качестве основы для сопоставления со значениями величин того же рода.

9.

9
Результат измерения представляют именованным числом единиц измерения
величины с указанием погрешности измерения.
Для измерения, в котором имеют место повторные показания, каждое
показание может использоваться, чтобы получить измеренное значение величины,
например, среднее арифметическое, обычно с меньшей погрешностью
(неопределенностью) измерений.
При равноточных многократных измерениях, когда все n измерений величины
х выполнены с одинаковой точностью, в качестве результата измерения величины
используют среднее арифметическое значение результатов измерений:
1 n
x xi ,
n i 1
где хi - результат i-го единичного измерения;
x - среднее арифметическое
значение измеряемой величины из n единичных результатов.

10.

10
ОБЪЕКТ
ИЗМЕРЕНИЯ
ЦЕЛЬ
ИЗМЕРЕНИЯ
ФВ1
ФВ2
ФВ3
...
ФВn
УСЛОВИЯ
ИЗМЕРЕНИЙ
МЕТОД
ИЗМЕРЕНИЯ
СРЕДСТВО
ИЗМЕРЕНИЯ
РЕЗУЛЬТАТ ИЗМЕРЕНИЯ
ОПОРНОЕ ЗНАЧЕНИЕ
ПОГРЕШНОСТЬ
(НЕОПРЕДЕЛЕННОСТЬ)
ИЗМЕРЕНИЯ
ИСТИННОЕ
ПРИНЯТОЕ
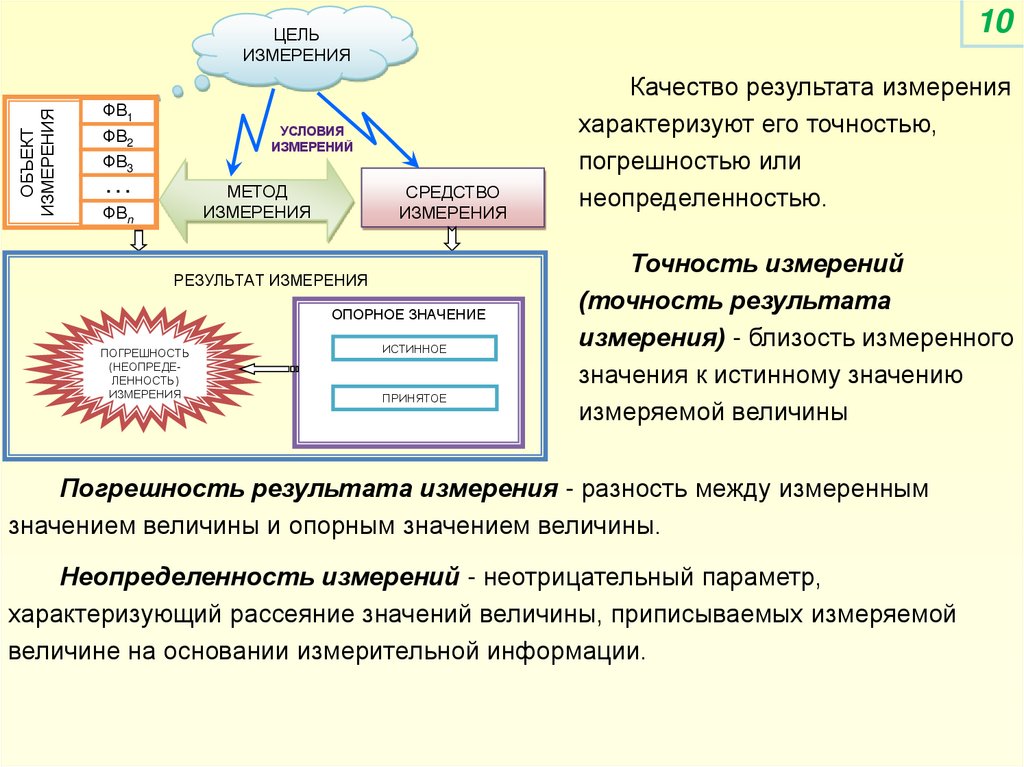
Качество результата измерения
характеризуют его точностью,
погрешностью или
неопределенностью.
Точность измерений
(точность результата
измерения) - близость измеренного
значения к истинному значению
измеряемой величины
Погрешность результата измерения - разность между измеренным
значением величины и опорным значением величины.
Неопределенность измерений - неотрицательный параметр,
характеризующий рассеяние значений величины, приписываемых измеряемой
величине на основании измерительной информации.

11.

Измерение как процесс включает в себя четыре основных этапа:
Этапы
1. Постановка
измерительной
задачи и
построение
математической
модели ОИ.
Формулировка
цели
11
Подэтапы
Анализ априорной информации
Формирование модели объекта
• какие физические величины или параметры объекта подлежат
измерению
•соответствие модели реальному объекту.
Определение измеряемой ФВ
Формирование основных уравнений измерения
Формулировка цели измерения
• какой точности должен быть результат измерения ?
•нестабильность измеряемых параметров модели в течение времени
измерения не должна превышать 10% от заданной погрешности модели
(за погрешность модели принимают размах предполагаемых результатов
измерений)
• в какой форме следует представить результат, чтобы это
соответствовало цели измерительной задачи?
а) если полученный результат измерения используется для сравнения с другими
результатами измерений или для дальнейших расчетов, - результат
измерений, оценки случайных и неисключенных систематических
погрешностей по отдельности представляют как точечные оценки;
б) если результаты измерений окончательны, суммарную погрешность
результата представляют как интервальную характеристику суммарной
погрешности.

12.

12
Этапы
Подэтапы
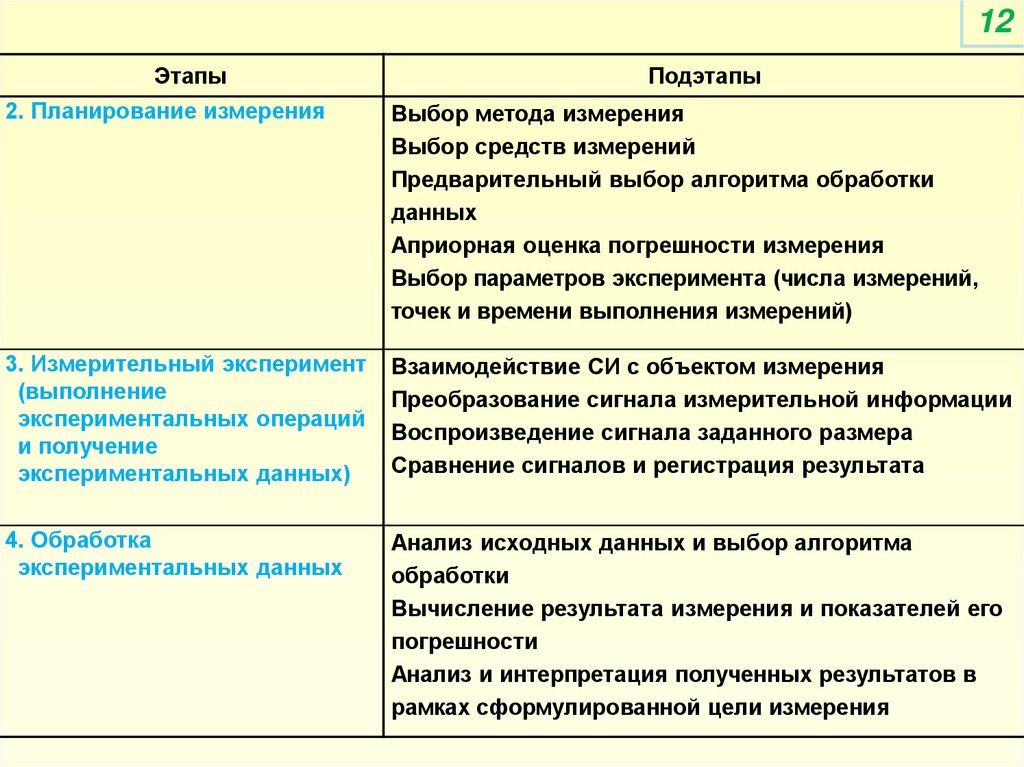
2. Планирование измерения
Выбор метода измерения
Выбор средств измерений
Предварительный выбор алгоритма обработки
данных
Априорная оценка погрешности измерения
Выбор параметров эксперимента (числа измерений,
точек и времени выполнения измерений)
3. Измерительный эксперимент
(выполнение
экспериментальных операций
и получение
экспериментальных данных)
Взаимодействие СИ с объектом измерения
Преобразование сигнала измерительной информации
Воспроизведение сигнала заданного размера
Сравнение сигналов и регистрация результата
4. Обработка
экспериментальных данных
Анализ исходных данных и выбор алгоритма
обработки
Вычисление результата измерения и показателей его
погрешности
Анализ и интерпретация полученных результатов в
рамках сформулированной цели измерения

13.

13
2.2. Классификация измерений
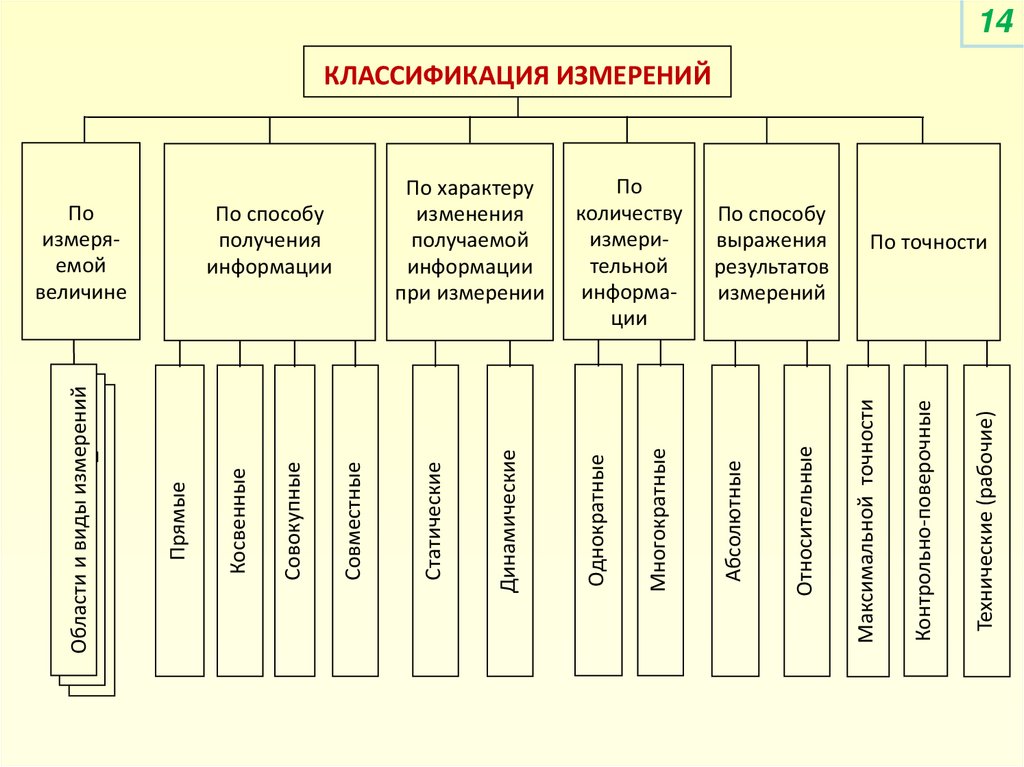
В теоретической метрологии проводят разветвлённую классификацию
измерений по признакам, определяемым структурой измерения. Измерения
различают по многим признакам, в том числе:
1. по измеряемой величине;
2. по способу получения информации;
3. по характеру изменения получаемой информации в процессе измерений (по
режиму использования СИ);
4. по количеству измерительной информации (наблюдений);
5. по отношению к основным единицам измерения (по способу выражения)
6. по точности.

14.

14
КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ
Технические (рабочие)
Контрольно-поверочные
По точности
Максимальной точности
Относительные
По способу
выражения
результатов
измерений
Абсолютные
Многократные
По
количеству
измерительной
информации
Однократные
Динамические
Совместные
Совокупные
Косвенные
Прямые
Области и виды измерений
Ви
ды
из
ме
рен
ий
По способу
получения
информации
Статические
По
измеряемой
величине
По характеру
изменения
получаемой
информации
при измерении

15.

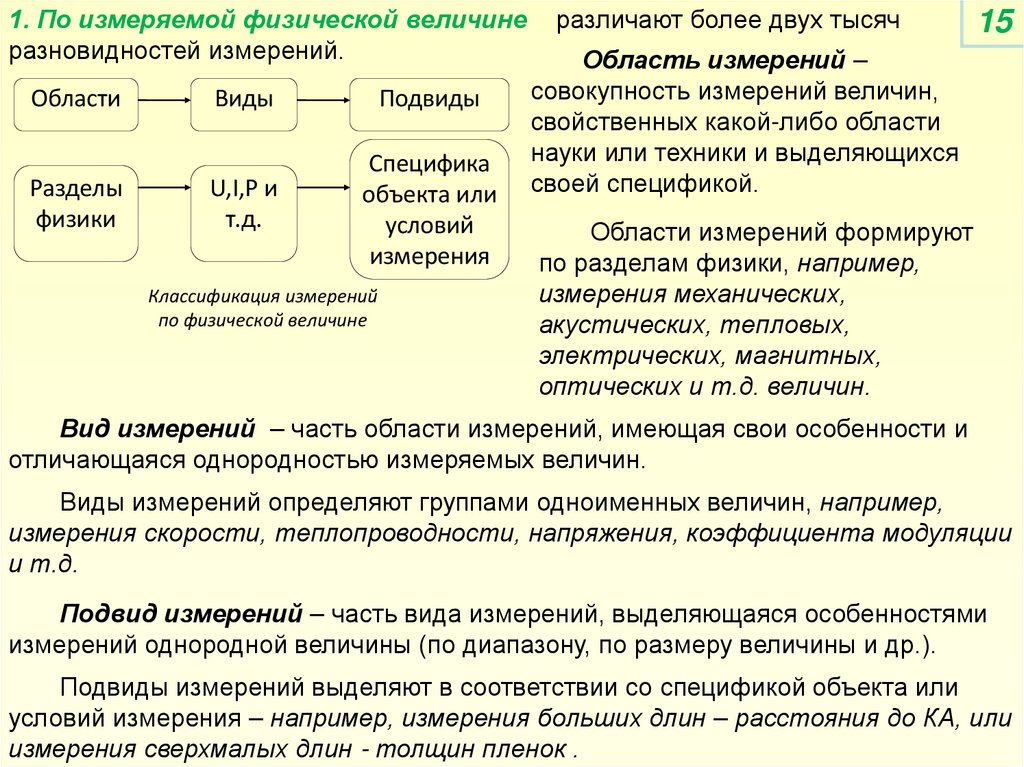
1. По измеряемой физической величине
разновидностей измерений.
Области
Разделы
физики
Виды
Подвиды
U,I,P и
т.д.
Специфика
объекта или
условий
измерения
Классификация измерений
по физической величине
различают более двух тысяч
15
Область измерений ‒
совокупность измерений величин,
свойственных какой-либо области
науки или техники и выделяющихся
своей спецификой.
Области измерений формируют
по разделам физики, например,
измерения механических,
акустических, тепловых,
электрических, магнитных,
оптических и т.д. величин.
Вид измерений ‒ часть области измерений, имеющая свои особенности и
отличающаяся однородностью измеряемых величин.
Виды измерений определяют группами одноименных величин, например,
измерения скорости, теплопроводности, напряжения, коэффициента модуляции
и т.д.
Подвид измерений ‒ часть вида измерений, выделяющаяся особенностями
измерений однородной величины (по диапазону, по размеру величины и др.).
Подвиды измерений выделяют в соответствии со спецификой объекта или
условий измерения – например, измерения больших длин – расстояния до КА, или
измерения сверхмалых длин - толщин пленок .

16.

2. По способу получения информации измерения разделяют на:
– прямые;
– косвенные;
– совокупные;
– совместные.
16
Прямое измерение ‒ измерение, при котором искомое значение величины
получают непосредственно от средства измерения.
При прямом измерении искомое значение физической величины находят
непосредственно путём сравнения с мерой этой величины.
Косвенное измерение ‒ измерение, при котором искомое значение величины
определяют на основании результатов прямых измерений других величин,
функционально связанных с искомой величиной .
При косвенном измерении искомое значение физической величины
определяют на основе известной зависимости между этой величиной и
величинами, получаемыми прямыми измерениями.
Y = f(x1,,x2...xn).
В ряде случаев вместо термина косвенное измерение применяют термин
косвенный метод измерений.

17.

Совокупные измерения ‒ проводимые одновременно измерения
17
нескольких одноименных величин, при которых искомые значения величин
определяют путем решения системы уравнений, получаемых при измерениях этих
величин в различных сочетаниях.
Число уравнений системы не должно быть меньше числа искомых величин.
Пример: измерение значения взаимоиндуктивности между двумя катушками.
1) Имеются катушки с индуктивностями L1 и L2.
2) Катушки соединяют так, чтобы их магнитные поля складывались, при этом
общая индуктивность LO1 = L1 + L2 + 2М, где М –
взаимоиндуктивность.
3) Катушки соединяют так, чтобы их магнитные поля вычитались, при этом
общая индуктивность LO2 = L1 + L2 ‒ 2М.
Значения LОl и LО2 получают с помощью прямых измерений.
4)
LО1 LО2
M
.
4
Совместные измерения ‒ проводимые одновременно измерения двух или
нескольких не одноименных величин для определения зависимости между ними.
rх = r0 + at + bt2

18.

18
3. По характеру изменения получаемой информации в процессе измерений
последние разделяют на:
– статические;
– динамические.
Статическое измерение ‒ измерение величины, принимаемой в
соответствии с конкретной измерительной задачей за неизменную на протяжении
времени измерения.
К статическим относят измерения параметров, которые в процессе
наблюдения не изменяются или рассматриваются неизменяющимися. Если
неизменности измеряемой величины достигнуть невозможно, то в этом случае
пределы допускаемых отклонений, должны быть несущественны по отношению к
номинальному значению измеряемой величины и указаны в технической
документации.

19.

19
Динамическое измерение ‒ измерение, при котором средства измерений
используют в динамическом режиме.
Динамический режим - режим использования средства измерений,
связанный с изменениями условий за время проведения измерительного
эксперимента, которые влияют на результат измерения (оценку измеряемой
величины), в т. ч. изменение измеряемой величины за время измерения.
В современных технологических и других процессах за время измерений
величины могут претерпевать те или иные изменения, и в этом случае измерения
называют динамическими.
Характерным для «чистых» динамических измерений является то, что
результат измерений изменяющейся во времени физической величины
представляют совокупностью её значений с указанием моментов времени,
которым соответствуют эти значения.
В других случаях результат динамического измерения может быть представлен
некоторым усреднённым числовым значением.

20.

4. По количеству измерений измерения разделяют на:
– однократные;
– многократные.
20
Однократное измерение ‒ измерение, выполненное один раз.
При однократных измерениях число измерений равняется числу измеряемых
величин.
На практике существует вероятность грубой ошибки – промаха. Для
исключения промахов рекомендуется выполнять не менее трёх-пяти измерений.
Если при этом результат измерения, т.е. значение физической величины,
полученное при измерениях, остается неизменным, то результат считают
полученным при однократном измерении. В противном случае переходят к
многократным измерениям.
Многократное измерение ‒ измерение физической величины одного и того
же размера, результат которого получен из нескольких следующих друг за другом
измерений, т.е. состоящее из ряда однократных измерений.
Многократные измерения – это измерения, при которых число измерений
n превышает число измеряемых величин. Обычно для многократных измерений
n ≥ 7.
Граница по количеству наблюдений определяется характером преобладающих
погрешностей и целесообразностью использования статистических методов
обработки.

21.

5. По способу выражения результатов различают:
– абсолютные;
– относительные.
21
Абсолютное измерение ‒ измерение, основанное на прямых измерениях
одной или нескольких основных величин и (или) использовании значений
физических констант
E mc2 ;
Понятие «абсолютное измерение» применяют как противоположное понятию
«относительное измерение» и рассматривается как измерение величины в ее
единицах.
Относительное измерение ‒ измерение отношения одноименных величин
или функций этого отношения.

22.

6. По точности различают:
22
– измерения максимальной точности;
– контрольно-поверочные измерения;
– технические (рабочие) измерения.
Измерения максимально возможной точности, достижимой при существующем
уровне развития науки и техники, связаны с использованием эталонов, с
измерением и использованием значений физических констант.
Контрольно-поверочные измерения – это измерения, погрешность которых
не должна превышать некоторых заданных значений. К этой группе относят
измерения, выполняемые службами надзора и измерительными лабораториями.
Технические (рабочие) измерения – это измерения, в которых погрешность
результата определяется характеристиками СИ и оценивается до проведения
измерений.
Технические измерения делят на равноточные и неравноточные.
Равноточные измерения – ряд измерений какой-либо величины,
выполненных одинаковыми по точности средствами измерений в одних и тех же
условиях с одинаковой тщательностью.
Неравноточные измерения – ряд измерений какой-либо величины,
выполненных различающимися по точности средствами измерений и (или) в
разных условиях.