interpolation_presentation

1.

Интерполяция функций
Методы Лагранжа, Чебышева и Ньютона
Специальные главы математики
17.01.2026

2.

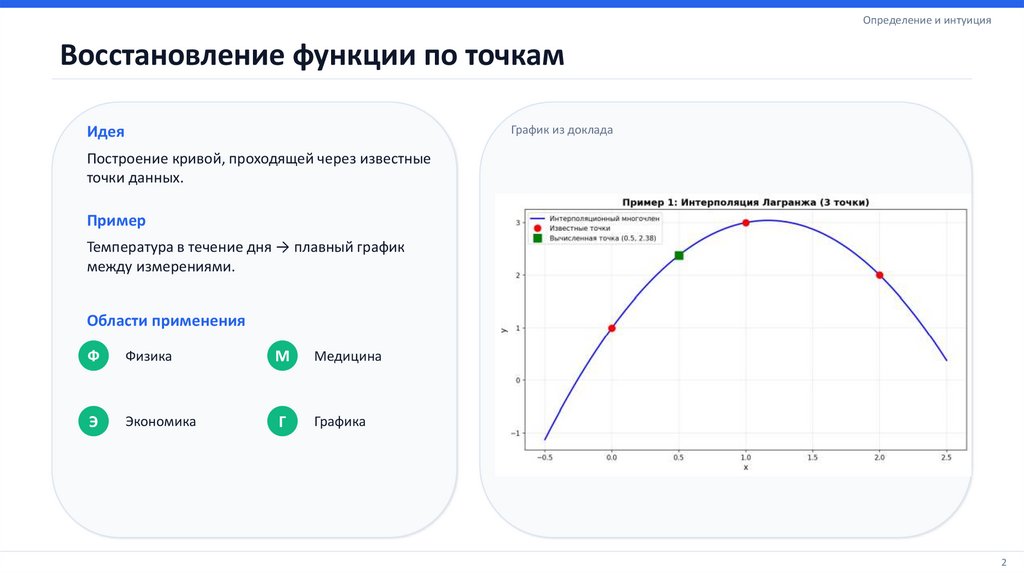
Определение и интуиция
Восстановление функции по точкам
График из доклада
Идея
Построение кривой, проходящей через известные
точки данных.
Пример
Температура в течение дня → плавный график
между измерениями.
Области применения
Ф
Физика
М
Медицина
Э
Экономика
Г
Графика
2

3.

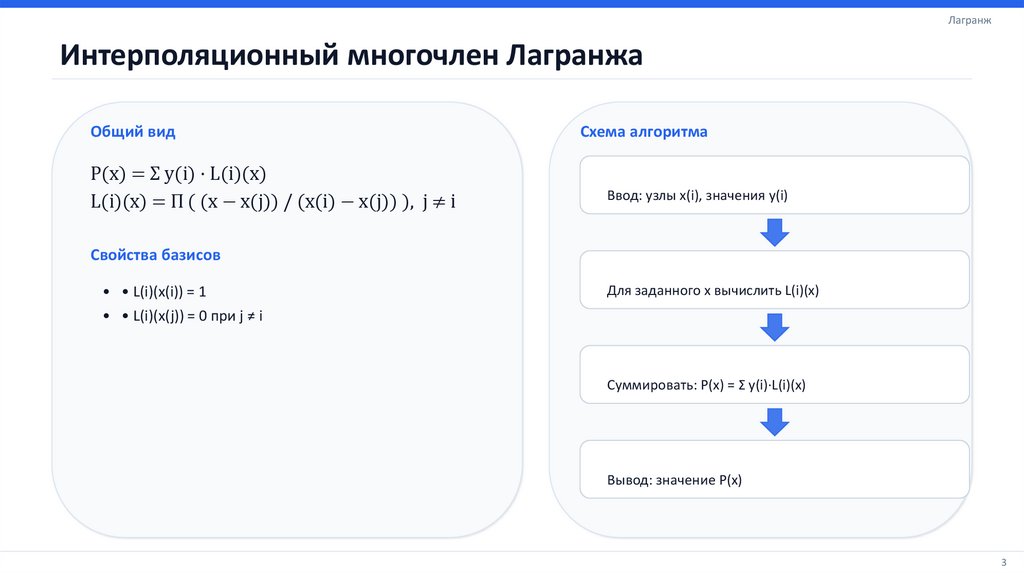
Лагранж
Интерполяционный многочлен Лагранжа
Общий вид
P(x) = Σ y(i) · L(i)(x)
L(i)(x) = Π ( (x − x(j)) / (x(i) − x(j)) ), j ≠ i
Схема алгоритма
Ввод: узлы x(i), значения y(i)
Свойства базисов
• • L(i)(x(i)) = 1
• • L(i)(x(j)) = 0 при j ≠ i
Для заданного x вычислить L(i)(x)
Суммировать: P(x) = Σ y(i)·L(i)(x)
Вывод: значение P(x)
3

4.

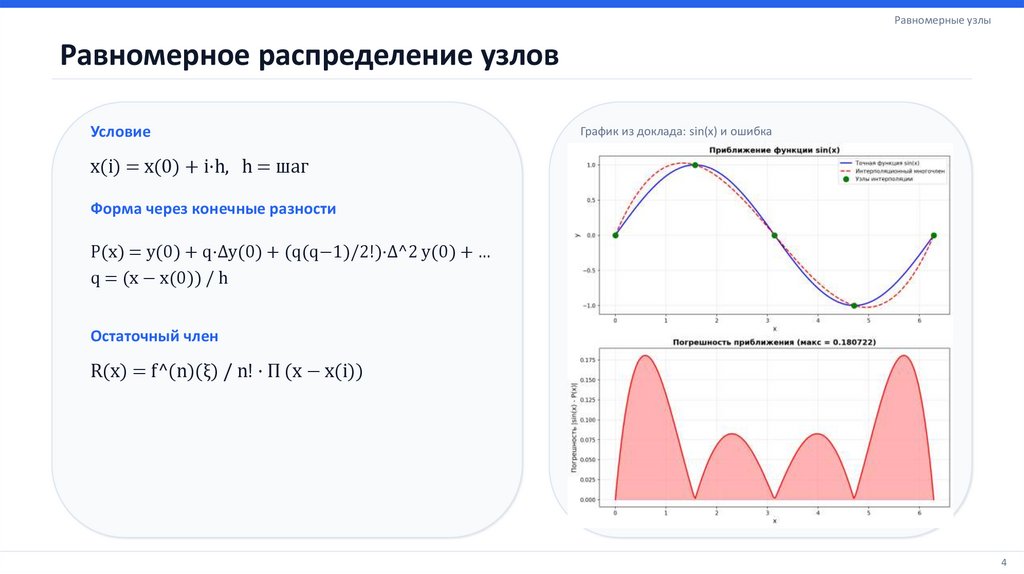
Равномерные узлы
Равномерное распределение узлов
Условие
График из доклада: sin(x) и ошибка
x(i) = x(0) + i·h, h = шаг
Форма через конечные разности
P(x) = y(0) + q·Δy(0) + (q(q−1)/2!)·Δ^2 y(0) + …
q = (x − x(0)) / h
Остаточный член
R(x) = f^(n)(ξ) / n! · Π (x − x(i))
4

5.

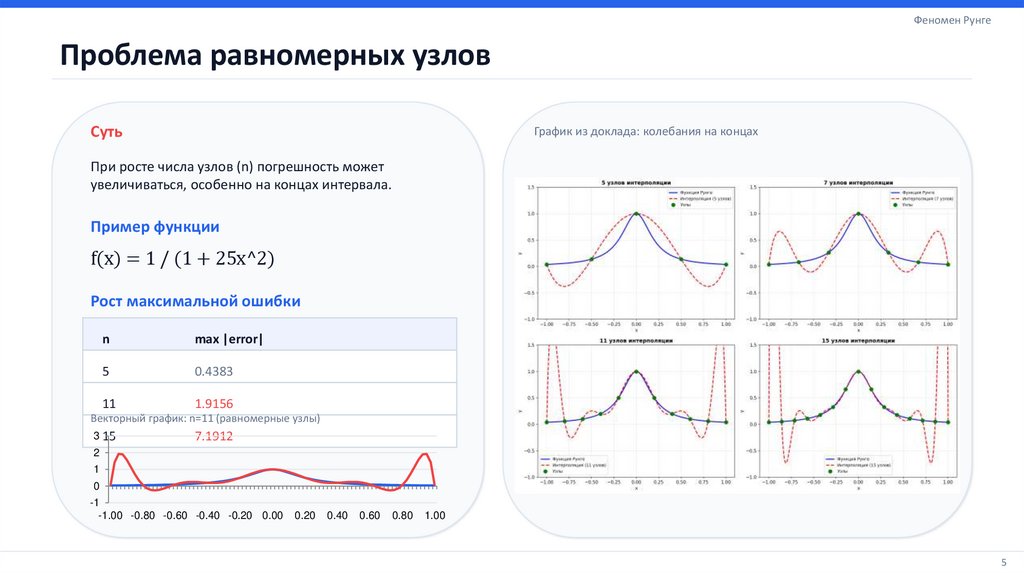
Феномен Рунге
Проблема равномерных узлов
Суть
График из доклада: колебания на концах
При росте числа узлов (n) погрешность может
увеличиваться, особенно на концах интервала.
Пример функции
f(x) = 1 / (1 + 25x^2)
Рост максимальной ошибки
n
max |error|
5
0.4383
11
1.9156
Векторный график: n=11 (равномерные узлы)
3 15
7.1912
2
1
0
-1
-1.00 -0.80 -0.60 -0.40 -0.20 0.00
0.20
0.40
0.60
0.80
1.00
5

6.

Узлы Чебышева
Решение проблемы Рунге
Формула
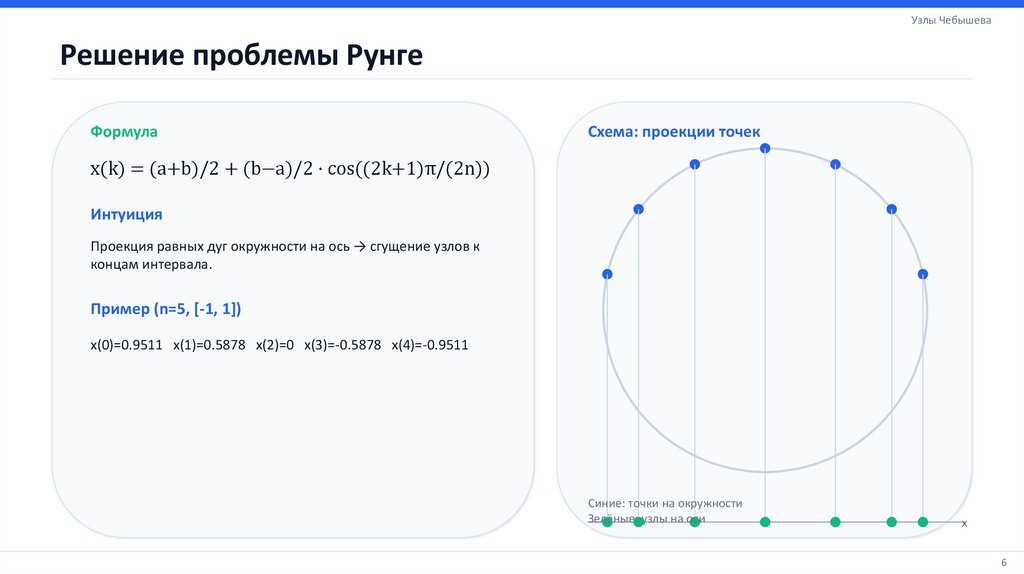
Схема: проекции точек
x(k) = (a+b)/2 + (b−a)/2 · cos((2k+1)π/(2n))
Интуиция
Проекция равных дуг окружности на ось → сгущение узлов к
концам интервала.
Пример (n=5, [-1, 1])
x(0)=0.9511 x(1)=0.5878 x(2)=0 x(3)=-0.5878 x(4)=-0.9511
Синие: точки на окружности
Зелёные: узлы на оси
x
6

7.

Из доклада
Сравнение
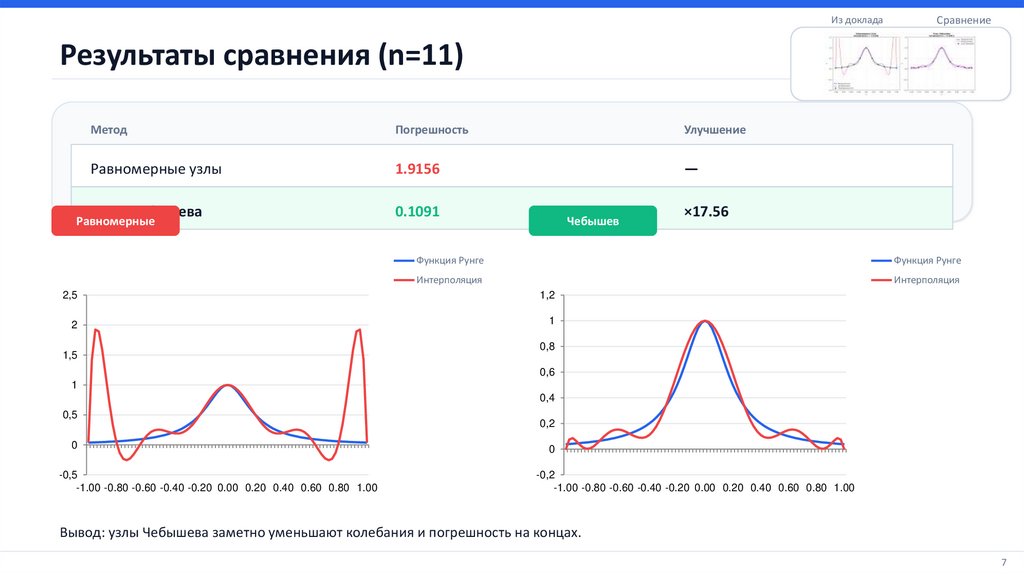
Результаты сравнения (n=11)
Метод
Погрешность
Улучшение
Равномерные узлы
1.9156
—
Узлы Чебышева
0.1091
Равномерные
Чебышев
Функция Рунге
Функция Рунге
Интерполяция
Интерполяция
2,5
1,2
2
1
1,5
×17.56
0,8
0,6
1
0,4
0,5
0
-0,5
-1.00 -0.80 -0.60 -0.40 -0.20 0.00 0.20 0.40 0.60 0.80 1.00
0,2
0
-0,2
-1.00 -0.80 -0.60 -0.40 -0.20 0.00 0.20 0.40 0.60 0.80 1.00
Вывод: узлы Чебышева заметно уменьшают колебания и погрешность на концах.
7

8.

Ньютон
Интерполяция Ньютона (кратко)
Основа: разделённые разности
P(x) = f[x(0)] + f[x(0),x(1)](x−x(0)) +
f[x(0),x(1),x(2)](x−x(0))(x−x(1)) + …
Пример кода (Python)
1 coef = divided_differences(x, y)
2 p = coef[0]
3 for k in range(1, n): p += coef[k] *
np.prod(x0 - x[:k])
Преимущество
Удобно добавлять новые узлы: пересчитывается только один
столбец разделённых разностей.
Здесь divided_differences вычисляет таблицу коэффициентов.
8

9.

Применения
Где используется?
Интерполяция — основа многих технологий, где данные заданы дискретно.
1
Графика
2
Кривые Безье и сплайны
4
Инженерия
Расчёты и аппроксимации
Финансы
Сглаживание и прогнозы
5
3
Медицина
Анализ сигналов и данных
Наука
Моделирование процессов
Ключевой вывод: интерполяция превращает набор точек в управляемую модель.
9

10.

Итоги
Итоги и выводы
• Лагранж — простая формула, но риск феномена Рунге при равномерных узлах.
• Чебышев — оптимальные узлы: меньше колебаний и меньшая погрешность.
• Ньютон — удобно для табличных данных и добавления новых узлов.
• Выбор метода зависит от интервала, гладкости функции и требований к точности.
Спасибо за внимание!
Вопросы?
10